高精度高分辨率重力异常模型作为一种基础地理数据,为测绘学、地球物理学和地球动力学等学科的研究和应用提供基础地球空间信息,并在经济、国防建设等方面有着广泛的应用[1],如在构建高精度大地水准面模型时提供分辨率更高的重力水准面,在军事上为远程武器弹道修正计算提供重力基准等。目前的研究中,国内外科学家主要在EGM2008、EGM96等全球重力场模型之间进行对比分析,或者在模型结果和实测重力值之间进行比对分析[2-4],对于利用实测重力数据构建重力异常模型的论述较少。本文利用华南某半丘陵半山地地区的269个重力点实测数据,选取不同的模型类型、建模算法和分辨率等内容制定方案进行建模。通过检验外符合精度,得出相关的结论。
1 重力/GPS数据的采集及处理 1.1 重力/GPS数据的采集采用某数字型相对重力仪,按照加密重力测量的要求采集了269个点的绝对重力值,重复测点检核的符合精度优于0.1 mGal。
采用某大地测量型接收机在每个点位采集20 min,部分观测条件不好的山地地区延长至30 min,采样间隔15 s,与已知点的距离不超过20 km,可保证大地高精度优于0.5 m。同时利用已有的该地区0.2 m精度高程异常模型,将大地高转换为1985高程系下的正常高。
1.2 重力异常的计算首先需要计算点位的正常重力值,采用1980正常重力公式[5]:
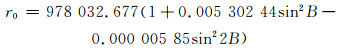
|
(1) |
式中,B代表大地纬度。
根据斯托克斯理论,空间重力异常为地面点重力值归算到大地水准面的重力值与椭球面正常重力之差,但其只考虑了地面到大地水准面的高度对重力的影响,没有考虑二者之间地层质量的影响[6]:
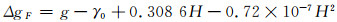
|
(2) |
式中,g代表实测重力值,H代表正常高,公式等号右侧后两项为空间改正项。
布格重力异常是在空间重力异常的基础上加入了地面到大地水准面间的地层质量对重力的影响。陆地上的改正公式为[6]:
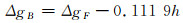
|
(3) |
式中, h为层间厚度,取正常高;等号右侧第二项为层间改正。
1.3 实测值与EGM2008结果的对比分析将计算得到的空间重力异常值与EGM2008模型2.5′分辨率空间重力异常格网的结果进行比对,见表 1(单位mGal)。
|
|
表 1 实测空间重力异常与EGM2008结果的比对 Tab. 1 Comparison of the measured spatial gravity anomaly and results from EGM2008 |
可以看出,EGM2008基本能够反映地表重力的整体变化情况,并且与实测值存在-11.9 mGal的系统性偏差,这是由于在中国区域缺少地表实测重力数据的支持,其他各项指标也与之前学者的研究结论[2, 7-8]一致。
2 建模分析 2.1 不同建模类型的对比分析重力异常模型包括空间重力异常模型和布格重力异常模型,分别建立这两种模型。在空间上,均匀选取约3/4的实测重力点(共202个)参与建模,采用直接建模的形式,算法采用曲面建模中的泛克里金法,该方法具有无偏性、方差最小等特点[9],其余67个点作为外符合检验点。结果见表 2(单位mGal)。
|
|
表 2 空间、布格重力异常模型结果与67个实测点数据的比对 Tab. 2 Comparison between tesults from space/Bouger gravity anomaly and data from 67 measuring points |
可以看出,布格重力异常模型各项指标远优于空间重力异常模型。这是由于布格异常加入了层间改正,即地面到水准面这部分地层质量的影响。布格异常模型数据比对实测值的平均值接近于0,最大、最小值约是标准差的2~3倍,说明布格模型较为准确地反映了实际重力情况。显然,布格重力异常更适合建立重力值内插模型。另一方面,实测数据建立的空间异常比对结果与§1.3 EGM2008的比对结果,除了平均值减小了10 mGal外,其余指标高度一致,印证了在整体趋势上,EGM2008空间重力异常与实际空间重力异常在华南地区可能存在一个10 mGal左右的系统差。再者,由于EGM2008并未提供布格重力异常模型,因此基于EGM2008空间重力异常模型的移去-恢复法不能直接应用于重力内插异常模型的建立。
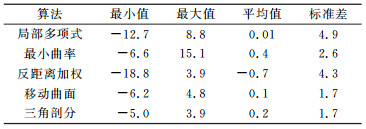
2.2 不同建模算法的对比分析按照§2.1中采用的建模点数、建模方法,选取不同的建模算法建立布格重力异常模型,结果见表 3(单位mGal)。
|
|
表 3 不同算法建模结果与67个实测点数据的比对 Tab. 3 Comparison between results from different algorithms for modeling and data from 67 measured points |
可以看出,移动曲面和三角剖分的各项指标最高,与泛克里金法基本一致。最小曲率次之,标准差为2.6 mGal,但最大值为15 mGal,约为标准差的5倍。局部多项式和反距离加权的标准差最大,分别为4.9 mGal和4.3 mGal。对于本例数据而言,移动曲面、三角剖分和泛克里金法精度相同,考虑到泛克里金法应用广泛,建模效果较为稳定[9-11],因此本文采用泛克里金法进行建模。
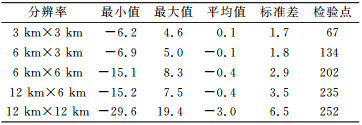
2.3 不同分辨率数据建模的对比分析按照§2.1建模方法,在空间上均匀选取1/2、1/4、1/8、1/16实测点建立布格重力异常模型,即分辨率约为6 km×3 km、6 km×6 km、12 km×6 km、12 km×12 km,采用泛克里金算法直接建模,其余点作为外符合检验点,结果见表 4(单位mGal)。
|
|
表 4 不同分辨率数据建模结果与其余实测点数据的比对 Tab. 4 Comparison between results from different resolution data modeling and data from other measured points |
可以看到,随着分辨率逐渐变大,均值除了12 km×12 km分辨率外基本为0,12 km×12 km分辨率建立模型的平均值为-3 mGal,这说明在半丘陵半山地地区,12 km分辨率的采样点建立的模型和实际重力已经出现了系统性的偏差,对于类似地形建立重力异常模型,实测点分辨率应该小于12 km×12 km。标准差随分辨率的增大而增大,分辨率为3 km×3 km时为2 mGal,6 km×6 km时为3 mGal,12 km×12 km时为6 mGal,最大、最小值从标准差的3倍逐渐增大到5倍左右,说明实测点分辨率降低引起模型效果逐渐发散。以上结果与李振海[12]等利用模拟数据得出的观测精度、分辨率与内插重力异常精度的结果基本一致。
通过以上比对分析,最后选择采用3/4点(即分辨率约为3 km×3 km)的实测数据,采用泛克里金法直接建模建立了该区域的布格重力模型,经过67个实测重力点的外符合精度检验,精度为1.7 mGal。
3 结语利用华南某半丘陵半山地约3 000 km2区域内的269个重力点实测数据,先与EGM2008空间重力异常模型进行比对,结果显示,该模型在中国华南地区有较好的符合效果,精度上可能存在一个10 mGal左右的系统差。分别建立了空间异常和布格异常模型,经过外符合检验发现,布格异常模型更加适用于建立内插重力异常模型。利用不同算法进行建模的结果显示,移动曲面、三角剖分和泛克里金法的精度相当,均优于最小曲率、局部多项式和反距离加权等方法。按不同分辨率选取实测数据建立布格异常模型,并进行精度分析发现,在山地丘陵地区建模数据分辨率在3 km×3 km、6 km×6 km、12 km×12 km时,精度分别为2 mGal、3 mGal、6 mGal左右。最后选取3 km×3 km分辨率实测数据,建立了该地区精度为1.7 mGal的布格重力异常模型。
| [1] |
冯林刚, 郅军义, 宝因乌力吉. 应用EGM2008模型和GPS/水准数据确定局部似大地水准面[J]. 测绘通报, 2011(1): 18-20 (Feng Lingang, Zhi Junyi, Baoin Wuliji. Determination of Local Quasi-Geoid Using EGM2008 Model and GPS/Leveling Data[J]. Bulletin of Surveying and Mapping, 2011(1): 18-20)
(  0) 0) |
| [2] |
章传银, 郭春喜, 陈俊勇. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 5-11 (Zhang Chaunyin, Guo Chunxi, Chen Junyong. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica at Cartographica Sinica, 2009, 38(4): 5-11)
(  0) 0) |
| [3] |
付广裕, 祝意青, 高尚华, 等. 川西地区实测自由空气重力异常与EGM2008模型结果的差异[J]. 地球物理学报, 2013, 56(11): 3 761-3 769 (Fu Guangyu, Zhu Yiqing, Gao Shanghua, et al. Discrepancies between Free Air Gravity Anomalies from EGM2008 and the Ones from Dense Gravity/GPS Observations at West Sichuan Basin[J]. Chinese Journal of Geophysics, 2013, 56(11): 3 761-3 769)
(  0) 0) |
| [4] |
齐显峰, 周巍, 崔吉春. EGM2008重力场模型计算中国地区垂线偏差分析[J]. 测绘技术装备, 2011(1): 6-8 (Qi Xianfeng, Zhou Wei, Cui Jichun. Analysis of China Area Vertical Deflection Calculation of EGM2008[J]. Geomatics Technology and Equipment, 2011(1): 6-8)
(  0) 0) |
| [5] |
郭俊义. 地球物理学基础[M]. 北京: 测绘出版社, 2001 (Guo Junyi. Fundamentals of Geophysics[M]. Beijing: Surveying and Mapping Press, 2001)
(  0) 0) |
| [6] |
GJB6304-2008. 2000中国大地测量系统[S] (GJB6304-2008.2000 China Geodetic System[S])
(  0) 0) |
| [7] |
李建成. 最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651-660 (Li Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model:Gravimetric Quasi-Geoid CNGG2011[J]. Acta Geodaetica at Cartographica Sinica, 2012, 41(5): 651-660)
(  0) 0) |
| [8] |
杨金玉, 张训华, 张菲菲, 等. EGM2008地球重力模型数据在中国大陆地区的精度分析[J]. 地球物理学进展, 2012, 27(4): 1 298-1 306 (Yang Jinyu, Zhang Xunhua, Zhang Feifei, et al. On the Accuracy of EGM2008 Earth Gravitational Model in Chinese Mainland[J]. Progress in Geophysics, 2012, 27(4): 1 298-1 306)
(  0) 0) |
| [9] |
羊远新, 戴中东, 魏桦. "移去-恢复法"在机场工程大比例尺测图控制网中的应用[J]. 测绘工程, 2012, 21(3): 44-48 (Yang Yuanxin, Dai Zhongdong, Wei Hua. Application of Remove-Restore Method in Large-Scale Topographical Mapping Control Network in Airport Construction[J]. Engineering of Surveying and Mapping, 2012, 21(3): 44-48 DOI:10.3969/j.issn.1006-7949.2012.03.011)
(  0) 0) |
| [10] |
牛文杰, 朱大培, 陈其明. 泛克里金插值法的研究[J]. 计算机工程与应用, 2001, 37(13): 73-75 (Niu Wenjie, Zhu Dapei, Chen Qiming. Reserch of Universal Kriging[J]. Computer Engineering and Applications, 2001, 37(13): 73-75 DOI:10.3321/j.issn:1002-8331.2001.13.025)
(  0) 0) |
| [11] |
刘海英.多种克里格方法在固矿储量估算中的应用研究[D].北京: 中国地质大学, 2010 (Liu Haiying.A Study on Application of Multiple Kriging Methods in Solid Mineral Reserve Estimation[D].Beijing: China University of Geosciences, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10491-2010250666.htm
(  0) 0) |
| [12] |
李振海, 罗志才, 汪海洪, 等. 给定内插重力异常精度时对重力数据的要求[J]. 武汉大学学报:信息科学版, 2011, 36(11): 1 328-1 331 (Li Zhenhai, Luo Zhicai, Wang Haihong, et al. Requirements for Gravity Data within the Given Accuracy of the Interpolated Gravity Anomaly[J]. Geomatics and Information Science of Wuhan Uniersity, 2011, 36(11): 1 328-1 331)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37