随着重力梯度仪精确度、效率的提高,近年来各国都在积极研究和开展航空重力梯度测量技术[1-3]。利用重力梯度测量数据,通过数据预处理、滤波、数据归算,将飞行高度处的重力参数向下调和延拓至大地水准面上,恢复重力场[4-6]。
在物理大地测量领域,位场延拓的常用方法是求解Poisson积分方程,许多学者先后提出和发展了各种有效的数值方法,主要有迭代法、配置法、直接代表法等[7]。这些方法有的在实际应用中受限于测区重力资料的缺失、测区范围的影响、边界效应的影响、重力异常协方差函数难以求得测区地形高数据等,会存在一些缺陷;有的停留在理论研究和实验上。在航空重力梯度测量数据的向下解析延拓中,会放大观测噪声和未模型化的信号,且当数据点间隔较小或延拓高度较大时,观测方程是病态的,求解向下延拓病态问题时应引入正则化处理[8]。
本文首先构建航空重力梯度测量向下解析延拓模型,将岭估计[9]、Tikhonov[10]和截断奇异值分解(TSVD)[11]3种正则化方法与L曲线[12]、留一交叉验证(OCV)[13]和广义交叉验证(GCV)[14]3种正则化参数选取方法相结合,并利用数值模拟计算,评价向下延拓数学模型的精度,分析不同正则化方法及参数确定方法的优劣,为实际应用提供依据。
1 基本原理 1.1 航空重力梯度测量向下解析延拓模型基于球谐分析,求解Laplace方程,将地球引力位表达成Fourier级数,建立地球扰动位与测线重力梯度观测值的函数关系,直接由测线重力梯度观测值得到扰动位系数。扰动位可展开成有限阶次的球谐级数:
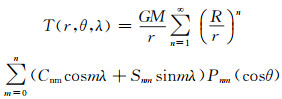
|
(1) |
式中,G为地球引力常数,M为地球总质量,R为地球平均半径,r为地心向径,φ为地心纬度,θ为地心余纬,φ+θ=90°,λ为经度,n和m为正整数,且m≤n,Cnm和Snm为完全规格化球谐系数,Pnm(cosθ)为完全规格化缔合Legendre函数。
由Molodensky边值条件[7],重力异常、扰动重力与扰动位满足如下近似关系:

|
(2) |
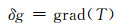
|
(3) |
重力梯度张量与引力位满足如下关系:
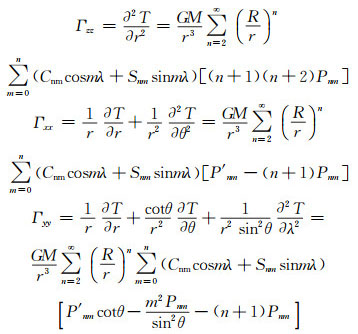
|
(4) |
基于矩谐分析恢复区域重力场的数学模型(式(2)、式(3))写成标准Gauss-Markov形式如下:
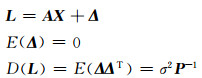
|
(5) |
其对应的法方程为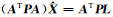
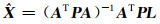
|
(6) |
其系数矩阵A的奇异值单调地趋向零,由式(6)难以获得稳定解。
1.2 正则化方法解决不适定问题的正则化方法就是用一些与原问题相邻近的适定问题的解去逼近原问题的解。如何建立“邻近”的问题,即构建正则化算子,且如何判断与原问题的“邻近程度”取决于合适的正则化参数,这些都是正则化方法的核心。
1.2.1 岭估计岭估计是从减小均方误差的角度出发提出的一种有偏估计方法,正则化解为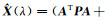
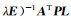
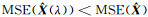
Tikhonov方法是在有限维空间上,以最小二乘准则为基础,对式(6)引入正则化矩阵和正则化参数,对解作约束,将问题转换为最优化问题:
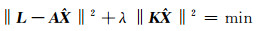
|
(7) |
式中,A、L及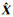
Tikhonov解应满足式(7)的最小化准则:
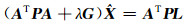
|
(8) |
式中,P为观测值的误差协方差矩阵,G=KTK为正定对称矩阵。式(8)的解可表示为
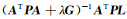
将式(6)总的权阵单位化,即P=I,对系数矩阵A∈Rm×n作奇异值分解(SVD):
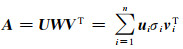
|
(9) |
其中,U=(u1, …, un)和V=(v1, …, vn)由矩阵A的左、右特征向量组成,且U∈Rm×n,V∈Rm×n,UTU=VTV=I;W=diag(σ1, …, σn)是非负对角阵,对角元素是矩阵A的奇异值,且按照非增次序排列,即σ1≥…≥σn≥0。
若对于设计矩阵A,有‖A‖2=σ1,则就较小奇异值σi,右特征向量vi存在:
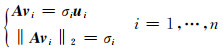
|
(10) |
当奇异值σ1呈阶梯状分布时,其特征向量ui、vi出现振荡现象(不可靠)。
SVD求解病态方程的关键是修改奇异值。将式(9)中的U、W、V按照以下形式分块:

|
(11) |
则经过截断奇异值分解(TSVD)的正则化方法处理的解为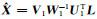
TSVD的关键是奇异值的选用个数。该方法是直接舍弃矩阵A小的奇异值及对应的特征向量,实际上是去除模型参数中不可靠的部分,用以减小解的方差,达到稳定解的作用。取过滤因子fλ(σ1)(λ表示一阈值),使得:
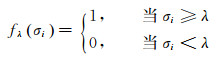
|
(12) |
若σ1≥σ2≥…≥σk≥λ≥σk+1≥…≥σn≥0,则
TSVD方法等价于用矩阵Ak=Umndiag(σ1, …, σk, 0, …, 0)VnnT逼近系数矩阵A,即用AkX=L逼近AX=L的解。
1.3 正则化参数的确定正则化参数不仅与系数矩阵A的特征值的收敛速度有关,且与观测值的精度有关。观测值及其单位权方差σ0是计算正则化参数必不可少的两个量。若已知正则化参数λ,由§1.2中的正则化方法可求解向下延拓的病态方程。只有合理的正则化参数才能使得观测误差与正则化误差之和位于其极小值附近,来抑制观测噪声高频部分对参数估值的影响,得到稳定的延拓解。
1.3.1 L曲线法对于式(7),首先计算残差的2范数Ω=‖L-AX‖2和参数的信号范数ρ=‖X‖2,并取自然对数,得到对应不同正则化参数的点值(ln(‖X‖2), ln(‖L-AX‖2));然后取曲线上曲率最大的点,使得拟合残量L-AX与X的解同时保持在较小的水平上,该点即定义为最优正则化参数。
对于TSVD方法,正则化参数是奇异值分解的截断数k,对应的L曲线是一系列离散的点(ln(‖Xk‖2), ln(‖L-AXk‖2)),k=1, 2, …, n构成的离散曲线,其最大曲线先用三次样条曲线拟合,再求最大曲率。取左边最靠近最大曲率点的离散点k为截断数。
1.3.2 OVC法基于式(8),采用留一交叉验证法求取正则化参数时,用A′ =Z1/2AG-1/2、L′ =Z1/2代替矩阵A、L,Z为观测值的协方差阵。参数的选择:去除一个观测数据,计算待求参数;然后计算交叉验证残差,即去除点的观测值与模型估值之差。
第i个观测值的交叉验证残差记为
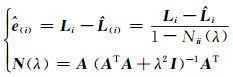
|
(13) |
其中,Li为第i个观测值,
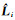
OCV方法选择正则化参数的函数式为: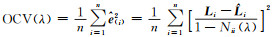
假设A′是将线性系统AX=L右端项L映射成正则解X(λ)的矩阵A′,即A′L=X(λ),称A′为影响矩阵。用广义交叉检验方法(GCV)确定正则化参数λ, 使得:
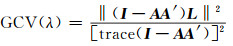
|
(14) |
关于参数λ极小,其中trace表示矩阵的迹,trace(A)等于矩阵A的对角元素的代数和。
GCV选择正则化参数的函数式为:GCV(λ)= 
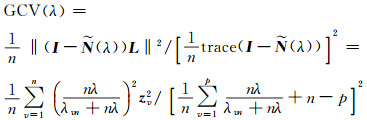
|
(15) |
其中,z=(z1, …,zn)T=UTL,U为A矩阵的奇异值分解矩阵,即A=UWVT,λvn为AAT矩阵的特征值v=1, 2, …, n。p=min(m, n),当v>p时,λvn=0。当GCV(λ)=min时,对应的λ为选定的正则化参数。
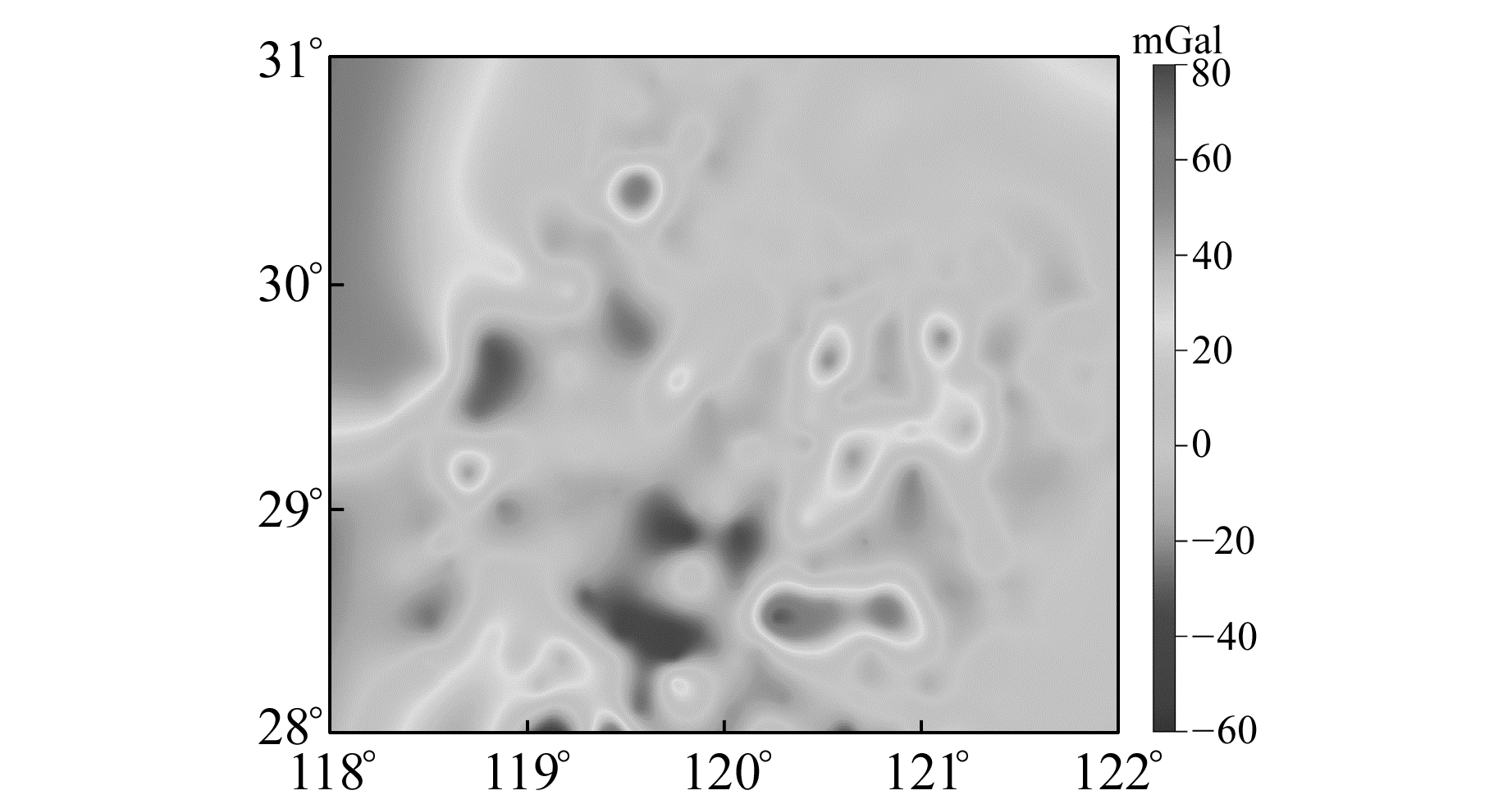
2 数值模拟计算为评价向下延拓数学模型、正则化及其参数确定方法的效果,以EGM2008的2~2 190阶位系数计算大地水准面上的扰动重力作为外部基准(真实值),对航空重力梯度数据向下延拓结果进行检核。信息统计见表 1(单位mGal), 空间分布见图 1。
|
|
表 1 真实扰动重力 Tab. 1 The real gravity disturbance |
|
图 1 EGM2008位模型计算扰动重力 Fig. 1 The gravity disturbance calculated by EGM2008 |
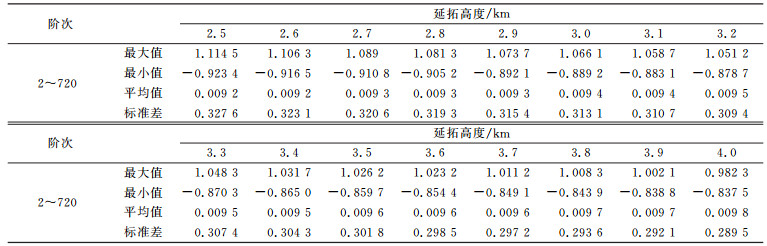
因无实测航空重力梯度数据,参考国内外航空重力测量技术的要求[1-4],飞行高度一般在2.8~3.5 km范围内,分别对不同飞行高度上的扰动重力梯度张量的对角线分量Γxx、Γyy、Γzz进行模拟(式(4)),并在模拟观测值中加入标准差为1.5 mGal的白噪声,模拟数据能以10-11E的精度满足Laplace方程[1-2, 4](见表 2, 单位10-11E)。对测线上的重力梯度观测值经数据预处理、滤波处理及地形改正后,构成的5′×5′扰动重力梯度张量,经纬度范围为72°~136°E、17°~54°N,以此作为实测数据,空间分布见图 2。

|
图 2 扰动重力梯度张量Γzz的模拟值 Fig. 2 The simulating values of Γzz |
|
|
表 2 扰动重力梯度张量对角线分量满足Laplace方程的精度 Tab. 2 The diagonal components of the gravity gradients that fulfill the precision of Laplace equation |
通过3种正则化法与3种参数选取方法组合,利用移去-恢复法[7, 15-16]消除向下延拓过程中的地形影响。将EGM2008重力位模型计算的扰动重力与空中扰动重力向下延拓的结果进行对比,空间分布见图 3。从表 3(单位mGal)统计结果可见,随着延拓高度的增大,延拓值与真实值的差值也在增大,说明在向下延拓过程中,高频观测噪声是被放大的,即可引入正则化方法,以抑制其对参数估值的影响,提高延拓精度。且在相同延拓高度上,不同的方法组合求解的延拓结果存在差异。

|
图 3 扰动重力延拓值与外部基准的差值 Fig. 3 The differene between continued values and external references |
|
|
表 3 扰动重力延拓值与外部基准的差值统计 Tab. 3 Statistics of differences between continued values and external references |
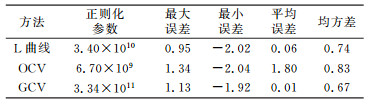
通过本文构建的模型分析正则化参数选取方法在正则化中的作用效果。图 4给出了在利用TSVD正则化方法求解过程中,L曲线、OCV、GCV方法求出的正则化参数(L拐点及OCV、GCV最小值用三角符号标出)。表 4给出了3种方法对应的外部检核误差信息:GCV方法对应的外部检核均方差最小,获得的最优参数相对稳定。

|
图 4 选取不同方法求解的正则化参数 Fig. 4 Regularization parameters calculated with different methods |
|
|
表 4 L曲线、OCV、GCV外部检核误差统计 Tab. 4 Statistics of errors with different parameter selection |
结合对比表 3与表 4的统计结果发现,TSVD正则化法与GCV参数选取方法的组合去噪效果明显,可以将重力场信号稳定地向下延拓,不论延拓高度相同或不同,其精度和稳定性都优于岭估计、Tikhonov正则化方法与相应参数选取方法的组合。
3 讨论1) 重力数据向下延拓解算的主要问题之一是奇异。奇异值分解SVD法解算向下延拓病态方程的关键是修改奇异值的技巧,TSVD正则化方法将小于某阈值的奇异值设为0,保留非零奇异值个数即为数据的有效自由度。本文利用不同的正则化算法和参数选取方法可以解决向下延拓解算的奇异问题。
2) 向下延拓的另一问题是解算的稳定性,主要受重力场高频信号(包括观测噪声)影响,EGM2008模型数据与航空数据存在明显的信号差异,文中通过对模拟观测值添加白噪声,对不稳定问题进行求解,以验证正则化算法结合正则化参数可有效抑制观测噪声高频部分对参数估值的影响。
3) 本文只对向下延拓的正则化算法进行了研究,但对该算法用于求解不同阶次、不同分辨率重力场的效率并未进行分析验证,且未与其他延拓方法的计算精度、稳定性进行比较分析,有待进一步研究。
4 结语通过构建航空重力梯度测量解析延拓模型,从向下延拓病态理论的研究入手,给出了3种正则化方法及其约束准则,将不同的参数选取方法与正则化方法结合,对向下延拓病态问题进行求解。通过模拟计算分析,得出:
1) 航空重力梯度测量数据的向下延拓是信号放大的非平稳过程,属不稳定问题的求解。利用TSVD正则化结合GCV参数选取方法能够得到重力场信号向下延拓的稳定解,在相同和不同的延拓高度上,其计算精度、稳定性等方面都优于其他组合方法。在实际航空重力梯度数据处理中应将此计算方法作为首选。
2) 在航空重力梯度数据向下延拓过程中,应考虑到地形起伏对重力场的影响,通过合适的方法解决该影响,提高延拓精度,使航空重力梯度测量从研究转入应用,成为局部重力场逼近和大地水准面确定的稳定技术。
| [1] |
Colm A M. The Air-FTGTM Airborne Gravity Gradiometer System[C]. Airborne Gravity 2004, Australia, 2004 https://www.researchgate.net/publication/286352496_The_Air-FTG_airborne_gravity_gradiometer_system
(  0) 0) |
| [2] |
Jekeli C. A Review of Gravity Gradiometer Survey System Data Analyses[J]. Geophysics, 1993, 58(4): 508-514 DOI:10.1190/1.1443433
(  0) 0) |
| [3] |
Wei M, Schwarz K P. Flight Test Results from Astrapdown Airborne Gravity System[J]. Journal of Geodesy, 1998, 72(6): 323-332 DOI:10.1007/s001900050171
(  0) 0) |
| [4] |
张昌达. 航空重力测量和航空重力梯度测量问题[J]. 工程地球物理学报, 2005, 2(4): 282-291 (Zhang Changda. On the Subject of Airborne Gravimetry and Airborne Gravity Gradiometry[J]. Chinese Journal of Engineering Geophysics, 2005, 2(4): 282-291 DOI:10.3969/j.issn.1672-7940.2005.04.007)
(  0) 0) |
| [5] |
Barnes G, Lumley J. Processing Gravity Gradient Data[J]. Geophysics, 2011, 76(2): 133-147
(  0) 0) |
| [6] |
Christensen A N, Dransfield M H. Noise and Repeatability of Airborne Gravity Gradiometry[C]. 76th EAGE Conference and Exhibition 2014 https://www.researchgate.net/publication/266635171_Noise_and_Repeatability_of_Airborne_Gravity_Gradiometry
(  0) 0) |
| [7] |
Moritz H. Advancedphysical Geodesy[M]. Herbert Wichmann Verlag, Karlsruhe, 1980
(  0) 0) |
| [8] |
Xu P L. Determination of Surface Gravity Anomalies Usinggradiometric Observables[J]. Geophysical Journal International, 1992, 110(2): 321-332 DOI:10.1111/gji.1992.110.issue-2
(  0) 0) |
| [9] |
Hoerl A E, Kennard R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems[J]. Technometrics, 1970, 12(1): 55-67 DOI:10.1080/00401706.1970.10488634
(  0) 0) |
| [10] |
Tikhonov A N, Glasko V B. Use of the Regularization Method in Non-Linear Problems[J]. USSR Computational Mathematics and Mathematical Physics, 1965, 5(3): 93-107 DOI:10.1016/0041-5553(65)90150-3
(  0) 0) |
| [11] |
Hansen P C. The Truncated SVD as A Method for Regularization[J]. BIT Numerical Mathematics, 1987, 27(4): 534-553 DOI:10.1007/BF01937276
(  0) 0) |
| [12] |
Hanke M. Limitations of the L Curve Method in Ill-Posed Problems[J]. BIT Numerical Mathematics, 1996, 36(2): 287-301 DOI:10.1007/BF01731984
(  0) 0) |
| [13] |
Shao J. Linear Model Selection by Cross-Validation[J]. Journal of the American Statistical Association, 1993, 88(422): 486-494 DOI:10.1080/01621459.1993.10476299
(  0) 0) |
| [14] |
Golub G H, Heath M, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223 DOI:10.1080/00401706.1979.10489751
(  0) 0) |
| [15] |
Novák P, Kern M, Schwarz K P, et al. Evaluation of Band-Limited Topographical Effects in Airborne Gravimetry[J]. Journal of Geodesy, 2003, 76(11-12): 597-604 DOI:10.1007/s00190-002-0282-5
(  0) 0) |
| [16] |
Dransfield M, Zeng Y. Airborne Gravity Gradiometry: Terrain Corrections and Elevation Error[J]. Geophysics, 2009, 74(5): 137-142 DOI:10.1190/1.3151798
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37