2. 地球空间信息技术协同创新中心,武汉市珞喻路129号,430079
低轨卫星搭载星载GPS接收机,在轨实时处理GPS伪距和载波相位观测数据,为低轨卫星的姿态控制、对地观测等系统提供高精度的轨道参数。该实时定轨方法(有的文献称为自主定轨)已经发展成为低轨卫星轨道测控的主要技术手段。为了降低观测数据中的粗差和中断等因素对实时定轨的影响,同时提高轨道预报能力,实时定轨系统通常引入高精度的动力学模型,采用扩展卡尔曼滤波对卫星状态参数进行估计[1-4]。
实时定轨系统经过软件移植,在星上微处理器中实时运行,而星载微处理器大多采用DSP作为处理单元,计算能力和存储能力远低于PC系统[3]。因此,实时定轨系统所选用的动力学模型精度要远低于地面后处理定轨系统。对于大气阻力和太阳光压等非保守力,一般将阻力系数Cd和光压系数Cr设置为待估参数,提高非保守力的计算精度[1-6]。对于保守力来说,尤其是地球非球形引力部分,选取的重力场模型阶次越高,计算得到的引力加速度就越精确[7],但是所需要的计算量也越大,因此在实时定轨系统中,需要将重力场模型截断,取其低阶部分。
对事后精密定轨和星载GPS实时定轨来说,重力场模型阶次选择有很大的区别。在事后精密定轨中,定轨精度是关注的主要因素,因此在选取重力场模型时,可以尽可能选取较高的阶次[7-9]。而在实时定轨系统中,定轨计算的整个过程要在星载平台上完成,受限于星载处理器的计算性能,需要在定轨精度和计算量之间进行平衡,即在能够满足计算负荷要求的条件下尽可能提高定轨精度。重力场模型的阶次确定与卫星轨道高度存在密切关系[9-10],卫星轨道越低,若要达到一定的实时定轨精度指标,就必须提高模型阶次,在轨计算量随之增加。目前实时定轨系统在确定合适的重力场模型阶次和动力学模型的随机过程噪声时,大多采用经验法,即利用现有相近轨道高度的卫星数据,通过数据处理仿真计算确定动力学模型及其随机模型。该方法虽然可以获得较为合理的定轨结果,但难以达到最佳效果,在工程应用上存在一定的难度。
本文以EGM2008模型为基础,通过分析重力场模型截断误差与卫星轨道高度之间的关系,对现有多颗卫星的GPS实测数据进行实时定轨仿真处理,确定在一定的实时定轨精度指标下重力场模型的截断误差限值,最后用实验验证该方法的可行性。
1 重力场模型的截断误差地球的非球形引力对外部空间点的引力位可表示为:
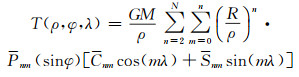
|
(1) |
式中,GM为地球引力常数;ρ为地心向径;φ、λ分别为地心纬度和地心经度;R为地球平均半径;Pnm(sinφ)为n阶m次规格化的勒让德函数;Cnm、Snm为规格化的地球重力场球谐系数;N为重力场模型的选取阶数。
在实时定轨的数据处理中,由于采用扩展卡尔曼滤波估计卫星轨道参数,所以轨道积分器通常使用4阶龙格-库塔单步积分方法。在向前积分一步时,需要计算4次非球形引力加速度。随着所选取重力场模型阶数N的增加,引力位的计算量将成倍增加。
为了在不影响实时定轨精度的情况下,尽可能减小计算量,在工程应用中需要确定合理的阶数N。舍去大于N的高阶部分将会产生一定的截断误差。为进一步得到截断误差,将式(1)对3个坐标分别求偏导数,得到非球形引力加速度,同时引入球面上的重力异常Δg,并取全球均方根,得到截断误差和扰动位系数的关系式,进一步借助莫里兹两分量模型简化计算,便可以得到不同阶次的重力场模型截断误差,详细公式见文献[11-13]。
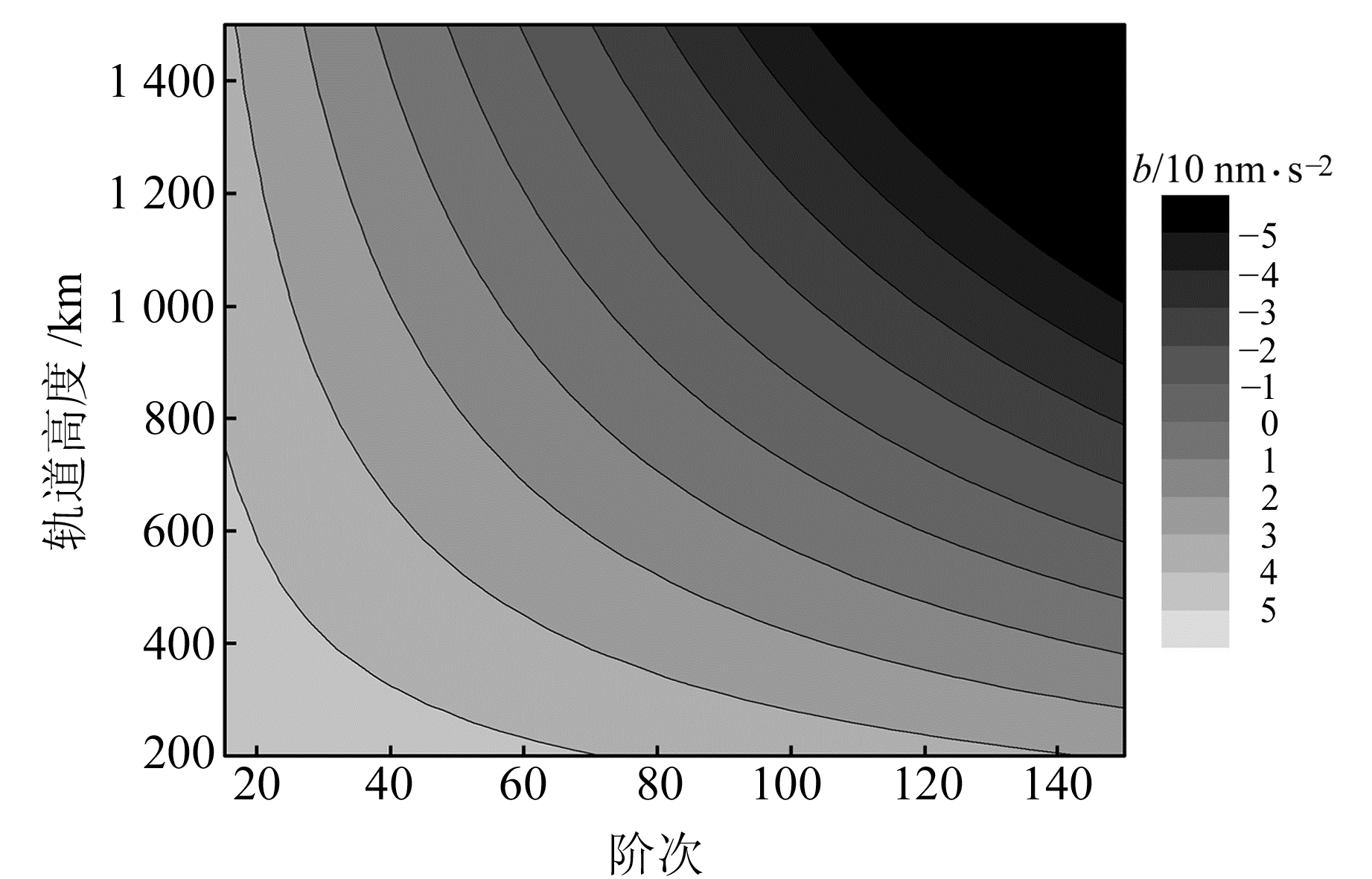
2 截断误差的影响因素分析从截断误差的计算公式可以看出,重力场模型的截断误差σ主要与卫星轨道高度ρ及模型阶次N有关。为了更直观地认识3者之间的关系,将低轨卫星轨道高度范围设置为200~1 500 km(以5 km为间隔),模型阶次N范围设置为15~150阶次(以5阶次为间隔),按照文献[11-13]的方法计算N阶重力场模型的截断误差(3D),并取对数得到b,结果见图 1。可以看出:1)当模型截断误差量级相同时,卫星轨道高度与重力场模型阶次呈反比关系(如截断误差处于0~10 nm/s2时,400 km轨道高度需要150阶次模型,而1 400 km轨道高度仅需50阶次左右模型便足以满足);2)当卫星轨道高度不变时,使用模型的阶次越高,则截断误差量级越小;3)当使用的重力场模型阶次不变时,卫星轨道越高,截断误差量级越小。
|
图 1 不同高度下不同阶次模型的截断误差 Fig. 1 Truncation error of different order model at different height |
在用扩展卡尔曼滤波对星载GPS伪距或载波相位观测数据进行实时定轨处理时,影响定轨精度的因素有很多,除了重力场模型的截断误差外,低轨道高度的大气密度模型误差、伪距观测值误差、广播星历与钟差误差等也是非常重要的因素,因此无法根据实时定轨的精度指标来推导重力场模型截断误差的阈值。
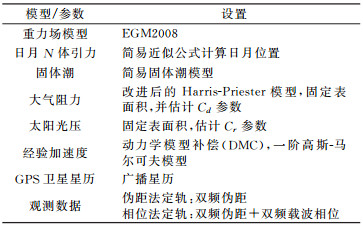
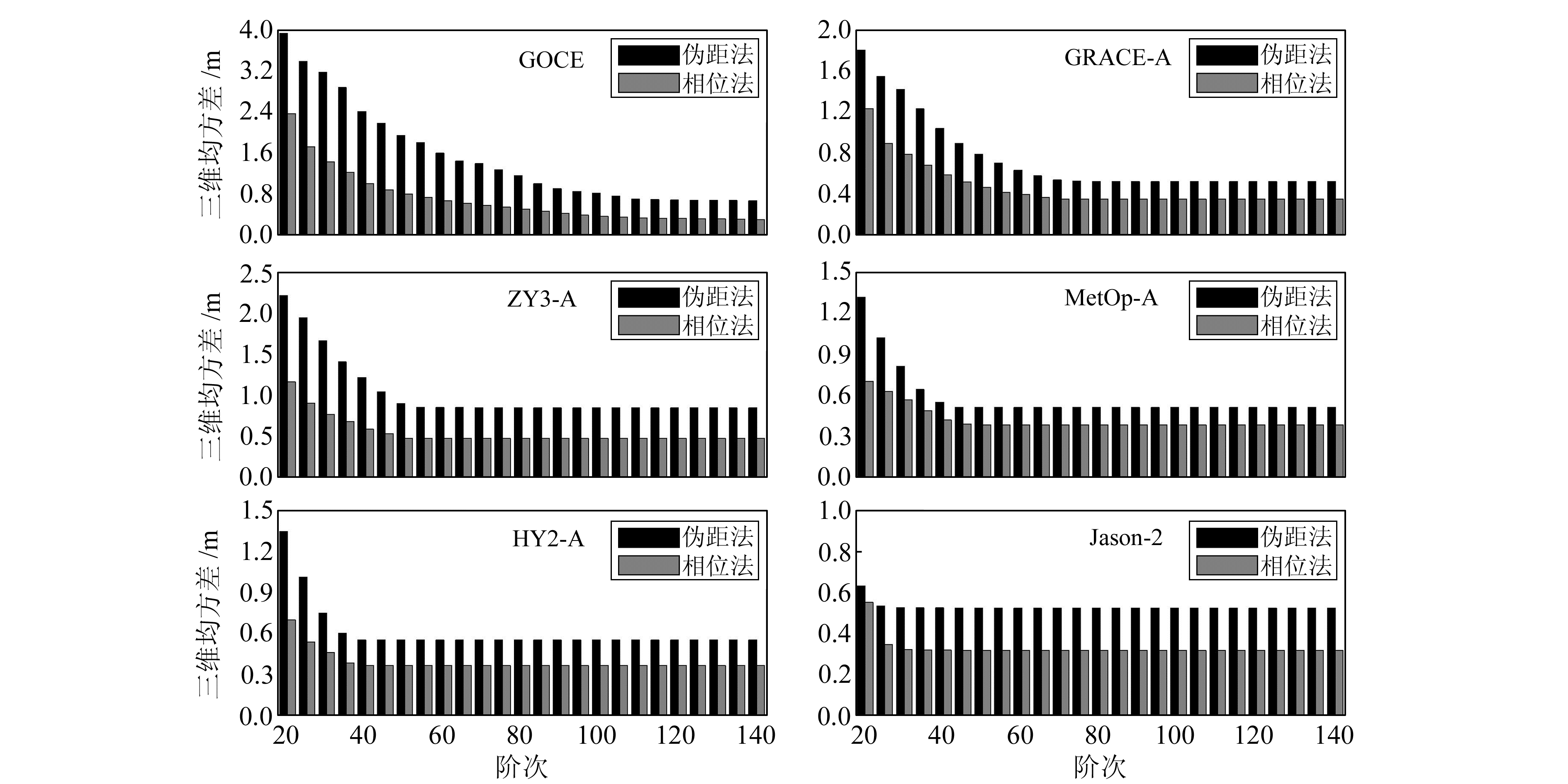
本文采用实时定轨数据处理仿真实验来分析定轨精度与重力场模型截断误差之间的关系。选取6颗不同轨道高度的低轨卫星GOCE(240 km)、GRACE-A(460 km)、ZY3-A(500 km)、MetOp-A(820 km)、HY2-A(900 km)和Jason-2(1 350 km),每颗卫星均搭载高性能双频GPS接收机。使用笔者自主研制的星载GPS实时定轨软件SATODS对每颗卫星的实测数据进行仿真分析,软件设置见表 1。该软件已经移植到DSP平台并应用到我国的低轨卫星上,用于实时定轨。本文采用的是PC版本,相同的实测数据和软件设置,实时定轨结果相同。在实验过程中,依次将重力场模型的阶次调整为20、25、30、…、140,并修改对应状态方程的过程噪声,其他设置不变,对每颗卫星分别进行伪距法实时定轨和载波相位法实时定轨,最后将定轨结果与相关数据分析中心(如JPL、CNES等)发布的精密轨道进行比较,实时定轨精度(3D RMS)的统计结果见图 2。
|
|
表 1 SATODS软件详细设置 Tab. 1 Strategies of orbit determination |
|
图 2 不同阶次的重力场模型对实时定轨精度的影响 Fig. 2 Influence of different order of earth gravity model to real-time orbit determination accuracy |
从图 2可以看出:1)使用相同阶次重力场模型的相位法定轨精度总是比伪距法定轨精度高,这是因为相位法定轨通过设置伪模糊度参数,很好地吸收了部分广播星历的轨道误差和钟误差[1-2];2)选取的重力场模型阶次较低时,实时定轨精度较差,随着模型阶次的增加,定轨精度逐渐提高,但是每颗卫星的重力场达到一定阶次时,定轨精度便趋于稳定,伪距法定轨精度达到0.8~1.0 m,相位法定轨精度达到0.3~0.6 m;3)卫星轨道越低,当实时定轨精度趋于稳定时,要求选取的重力场模型阶次越高;4)当实时定轨精度趋于稳定时,伪距法定轨与相位法定轨所需要选取的重力场模型阶次相当;5)我国ZY3和HY2-A卫星(搭载国产星载GPS接收机)的实时定轨精度及其变化趋势与国外卫星一致。
实际航天工程应用中,受星载处理器的计算能力和存储空间的限制,无法像事后精密定轨那样为了提高定轨精度,可以尽可能提高重力场模型的阶次。从另一角度来看,在实时定轨系统中,由于使用广播星历,GPS卫星位置误差与卫星钟差均为m级精度,当定轨精度趋于稳定时,重力场模型阶次的提高也不会进一步提高实时定轨的精度。因此,合理选取动力学模型及其随机模型,可以发挥实时定轨系统的最佳性能。
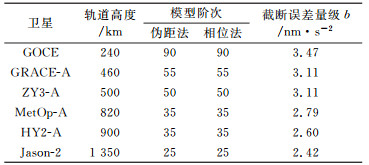
根据上述星载GPS实测数据的实时定轨仿真实验结果,实时定轨系统需要在定轨精度与计算负荷之间进行权衡,即在确保星载处理器的计算能力能够满足在轨计算负荷时,获得最佳的定轨精度。这里采用下述标准作为重力场模型阶次选择的最优确定结果:对于伪距法定轨,定轨精度达到1 m时,模型阶次提高5阶次引起的定轨精度的提高小于0.1 m;对于相位法定轨,当定轨精度达到0.5 m时,模型阶次提高5阶次引起的定轨精度的提高小于5 cm。以此确定的每颗卫星的最佳重力场模型阶次和不同轨道高度的重力场模型的截断误差见表 2。当星载处理器的计算性能较差时,可以选择低于最优重力场模型阶次,但是无法获得最佳的实时定轨精度。
|
|
表 2 最优重力场模型阶次及其截断误差 Tab. 2 Optimal determined order of earth gravity model and correspondent magnitude of truncation error |
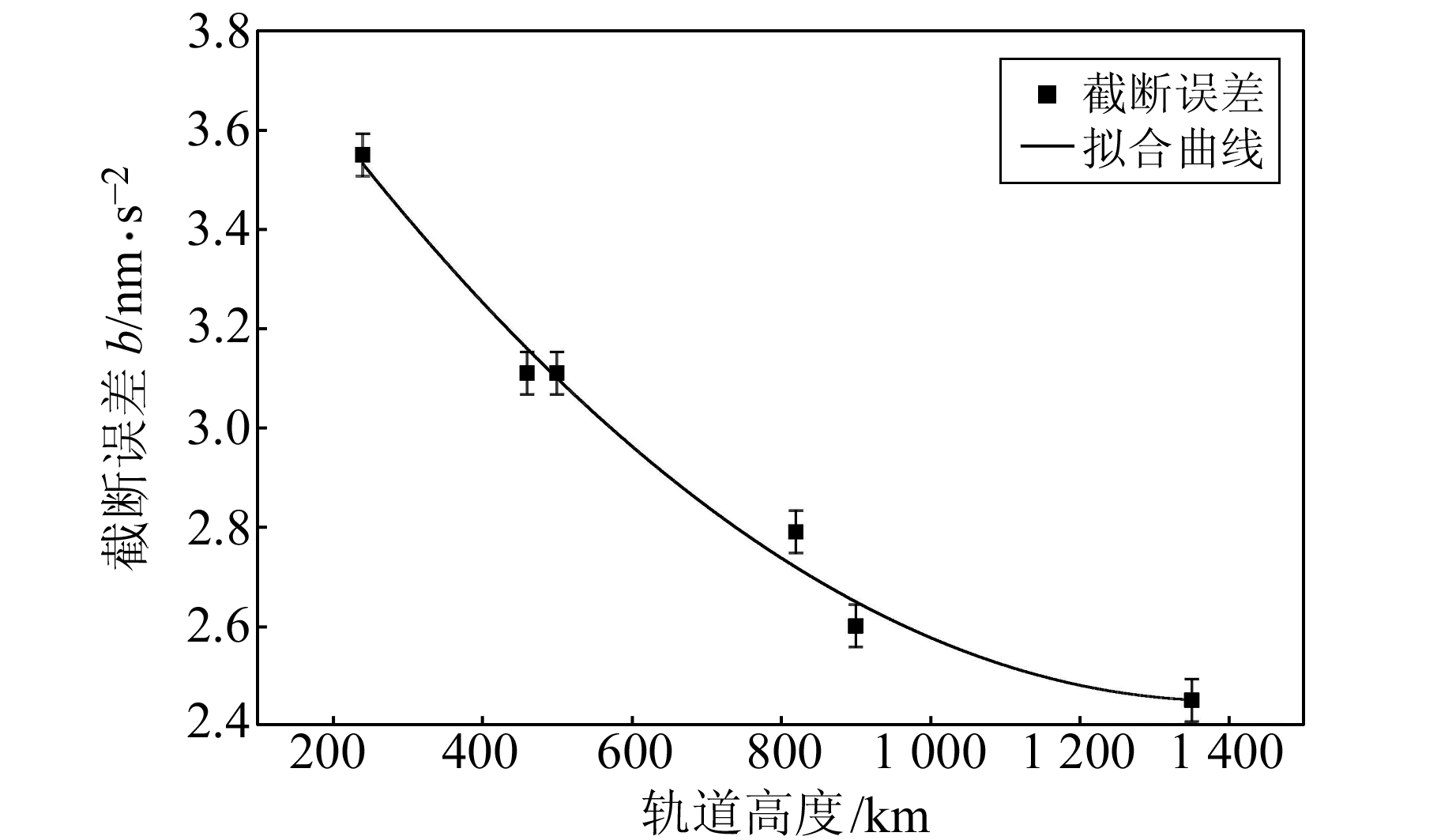
从表 2可以看出:1)伪距法定轨和相位法定轨所需要的重力场模型阶次相当;2)卫星轨道越低,实时定轨所需要的重力场模型阶次越大,对应的截断误差也越大。由此可知,实时定轨系统中,最优确定的重力场阶次及其截断误差与卫星轨道高度密切相关。为了更直观地了解重力场模型截断误差与卫星轨道高度之间的关系,将截断误差量级b与卫星轨道高度绘制成散点图,并用二次多项式进行拟合处理(图 3),得到拟合曲线式(2),每颗卫星的拟合残差均优于1倍的中误差。
|
图 3 截断误差及其拟合曲线 Fig. 3 Truncation error and correspondent fitting curve |

|
(2) |
式中,h为卫星轨道高度(km);b为截断误差量级(nm/s2)。
对于任意一颗低轨卫星,可以根据卫星的设计轨道高度,通过式(2)计算其截断误差量级b,然后根据截断误差计算公式反推其对应的最优重力场模型阶次,由此获得可靠的实时定轨精度指标。
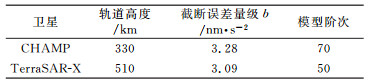
4 实验验证为进一步验证重力场模型阶次截断误差确定方法的可行性,选取CHAMP(330 km)、TerraSAR-X(510 km)2颗低轨卫星进行实验。这2颗卫星均搭载高精度双频星载GPS接收机,而且可以获得相关机构发布的精密轨道数据以验证实时定轨精度。
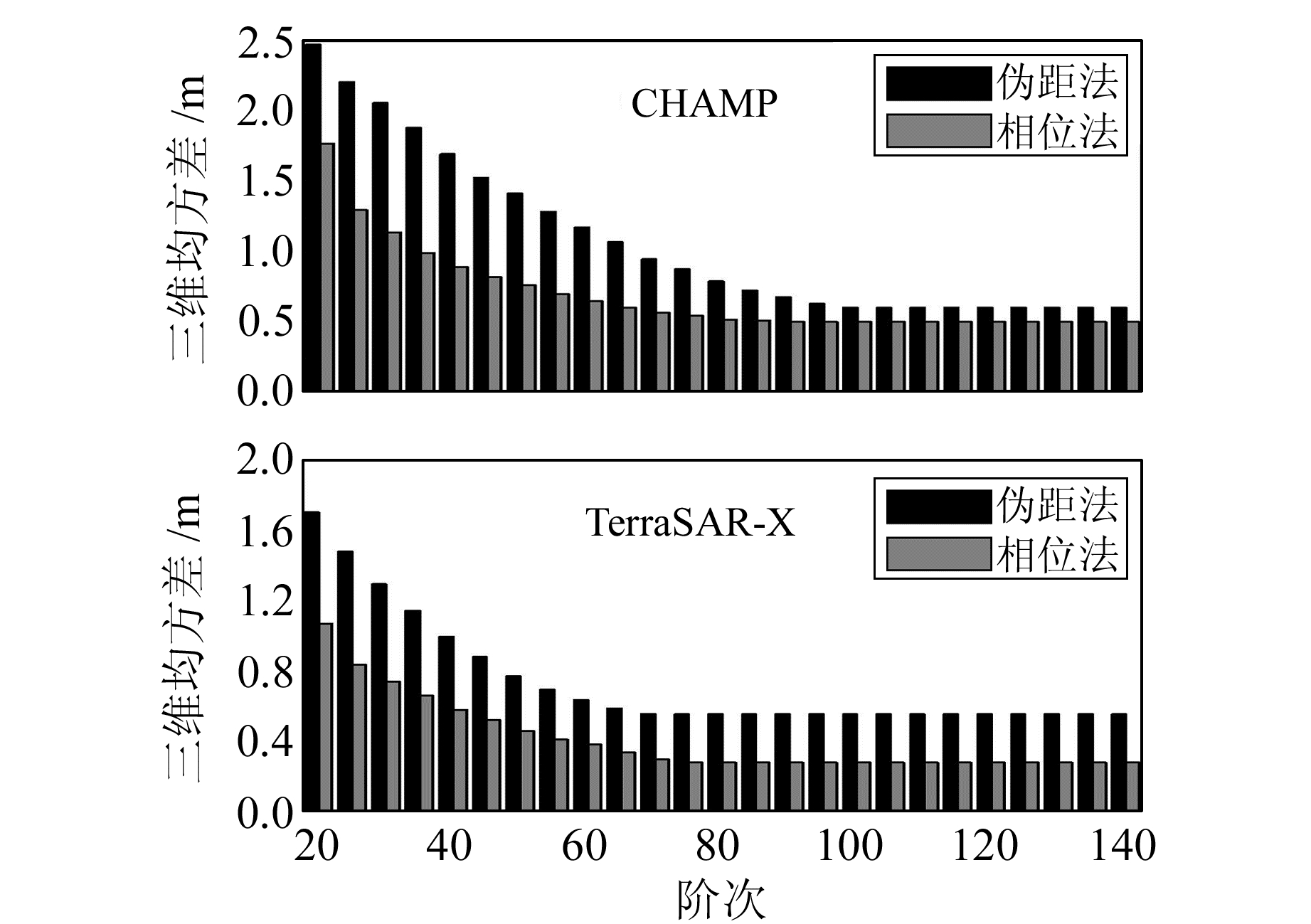
首先,根据这2颗卫星的轨道高度,结合式(2)和截断误差的计算公式,计算最优的截断误差量级b及对应的模型阶次(表 3)。然后,使用最优确定算法计算得到重力场模型阶次,分别对CHAMP、TerraSAR-X的实测数据进行伪距法和相位法实时定轨,软件设置与表 1相同,并对定轨结果与精密轨道进行求差和精度统计(3D RMS),结果见图 4。
|
|
表 3 最优重力场模型阶次及其截断误差 Tab. 3 Optimal determined order of earth gravity model and correspondent magnitude of truncation error |
|
图 4 不同阶次的重力场模型对实时定轨精度的影响 Fig. 4 Influence of different order of earth gravity model to real-time orbit determination accuracy |
可以看出,CHAMP、TerraSAR-X卫星进行星载GPS实时定轨时,重力场模型阶次分别达到70和50,伪距法定轨精度提高小于0.1 m,相位法定轨精度提高小于0.05 m,且伪距法实时定轨精度达到1.0 m以内,相位法定轨精度达到0.5 m以内。由此进一步验证了星载GPS实时定轨对重力场模型阶次的最优确定方法的可行性。
对于一颗新设计的卫星,已知卫星的轨道近似高度,就可以用上述方法确定实时定轨的重力场模型阶次,不需要事后根据精密星历进行仿真分析,卫星在轨实时定轨系统能够实现可靠的定轨精度指标。
5 结语星载GPS实时定轨系统中,在确定重力场模型阶次时,需要同时考虑定轨精度和计算负荷,在这2个方面进行最佳权衡。本文通过理论分析和仿真实验,提出了统计精度能够达到1.0 m(伪距法实时定轨)和0.5 m(相位法实时定轨)的重力场模型阶次的最优确定方法。如果使用的模型阶次大于本文的最优确定结果,实时定轨精度不会得到大幅提高,但是计算负荷将会明显增加。如果星载处理器性能有限,可以选择低于最优确定阶次的重力场模型,并配以合适的随机模型,但实时定轨精度指标将会一定程度地下降。
| [1] |
Wang F H, Gong X W, Sang J Z, et al. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver[J]. Sensors, 2015, 15(12): 30 403-30 418 DOI:10.3390/s151229805
(  0) 0) |
| [2] |
王甫红, 龚学文, 刘万科. 顾及广播星历误差分离吸收的分米级星载GPS实时定轨新方法[J]. 武汉大学学报:信息科学版, 2015, 40(9): 1 230-1 235 (Wang Fuhong, Gong Xuewen, Liu Wanke. A Novel Decimeter-Level Real-Time Orbit Determination Algorithm Using Space-Borne GPS Measurements with Separation and Absorption of Broadcast Ephemeris Error[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1 230-1 235)
(  0) 0) |
| [3] |
王甫红.星载GPS自主定轨理论及其软件实现[D].武汉: 武汉大学, 2006 (Wang Fuhong. Theory and Software Development on Autonomous Orbit Determination with Space-Borne GPS Measurements[D].Wuhan: Wuhan University, 2006) http://cdmd.cnki.com.cn/article/cdmd-10486-2008150697.htm
(  0) 0) |
| [4] |
龚学文.分米级星载GPS自主定轨关键技术与软件实现[D].武汉: 武汉大学, 2015 (Gong Xuewen. Key Technologies and Software Toward Decimeter-Level Autonomous Orbit Determination with Space-Borne GPS Carrier-Phase Measurements[D].Wuhan: Wuhan University, 2015)
(  0) 0) |
| [5] |
宋福香, 左文辑. 近地卫星的GPS自主定轨算法研究[J]. 空间科学学报, 2000, 20(1): 40-47 (Song Fuxiang, Zuo Wenji. Algorithm Study on Autonomous Orbit Determination for Low Earth Orbit Microsatellite Using GPS[J]. Chinese Journal of Space Science, 2000, 20(1): 40-47 DOI:10.3969/j.issn.0254-6124.2000.01.006)
(  0) 0) |
| [6] |
Svehla D, Rothacher M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003(1): 47-56
(  0) 0) |
| [7] |
罗志才, 钟波, 宁津生, 等. GOCE卫星轨道摄动的数值模拟与分析[J]. 武汉大学学报:信息科学版, 2009, 34(7): 757-760 (Luo Zhicai, Zhong Bo, Ning Jinsheng. Numerical Simulation and Analysis for GOCE Satellite Orbit Perturbations[J]. Geomatics and Information Science of Wuhan University, 2009, 34(7): 757-760)
(  0) 0) |
| [8] |
Bock H. Efficient Methods for Determining Precise Orbit of Low Earth Orbiters Using the Global Positioning System[D].Berne: Astronomical Institute of University of Berne, 2003 http://adsabs.harvard.edu/abs/2003GGAS...65.....B
(  0) 0) |
| [9] |
韩保民, 许厚泽. 重力场恢复中的基于星载GPS的低轨卫星简化动力学定轨方法研究[J]. 地球物理学进展, 2007, 22(1): 73-79 (Han Baomin, Xu Houze. GPS Based Reduced Dynamic Orbit Determination for Gravity Field Recovery[J]. Process in Geophysics, 2007, 22(1): 73-79 DOI:10.3969/j.issn.1004-2903.2007.01.010)
(  0) 0) |
| [10] |
张德成, 赵春梅, 郑作亚. 重力场模型对低轨卫星定轨的影响[J]. 大地测量与地球动力学, 2014, 34(2): 142-145 (Zhang Decheng, Zhao Chunmei, Zheng Zuoya. Influence of Gravity Field Models on Orbit Determination of LEOs[J]. Journal of Geodesy and Geophysics, 2014, 34(2): 142-145)
(  0) 0) |
| [11] |
张哞.快速逼近弹道扰动引力的算法研究[D].郑州: 信息工程大学, 2007 (Zhang Mou. A Study on Fast Computation of Trajectory Disturbing Gravity[D].Zhengzhou: Information Engineering University, 2007) http://cdmd.cnki.com.cn/article/cdmd-90008-2008044481.htm
(  0) 0) |
| [12] |
翟振和, 任红飞, 孙中苗. 重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J]. 测绘学报, 2012, 41(2): 159-164 (Zhai Zhenhe, Ren Hongfei, Sun Zhongmiao. Construction of Gravity Anomaly Degree Variance Model and Application in Computation of Spectral Sensitivity of Disturbing Gravity Functions[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 159-164)
(  0) 0) |
| [13] |
夏哲仁, 盛宗琪, 李迎春. 外空扰动引力场的传播特性[J]. 地球物理学报, 1998, 41(4): 484-493 (Xia Zheren, Sheng Zongqi, Li Yingchun. Propagation Properties of Disturbing Gravity Field Outside the Earth[J]. Chinese Journal of Geophysics, 1998, 41(4): 484-493 DOI:10.3321/j.issn:0001-5733.1998.04.007)
(  0) 0) |
2. Collaborative Innovation Center for Geospatial Technology, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37