相对于传统的转子陀螺,MEMS陀螺仪具有体积小、功耗低、重量轻、易于批量生产、成本低等诸多优点[1-3]。芯片化的集成使陀螺易于实现数字化和智能化,因此MEMS陀螺仪在汽车、电子设备、航空航天等领域具有广阔的应用前景。国内MEMS陀螺仪的测量精度相对于传统陀螺还有很大差距,无法满足应用需求。因此,立足于当前低精度的MEMS陀螺,使用算法来提高其精度,使其满足应用需求具有重要意义。
目前提高MEMS陀螺精度的方法主要包括以下3种:1)通过神经网络[4]、小波分析[5]等方法对陀螺进行建模;2)将子空间辨识方法和局域波分解法[6]应用到MEMS的随机误差建模中;3)将多种建模算法结合,如基于遗传算法的小波神经网络[7]等。但是通过以上方法提高的陀螺精度非常有限。本文探讨了6个陀螺阵列组成的虚拟陀螺技术,可以极大地提高陀螺精度。
1 MEMS陀螺的自回归模型和输出模型为了使用卡尔曼滤波对多个陀螺的输出数据进行融合,首先需要建立单个MEMS陀螺的自回归模型和输出模型,然后建立陀螺阵列的量测方程和状态空间方程。
构建卡尔曼滤波器时选取陀螺阵列的输入角速度为状态量,因此需要对单个陀螺的输入角速度进行建模才能构建出状态空间方程。以往的文献通常采用随机游走来描述陀螺的角速度,其局限性在于缺少功率谱密度和带宽等先验信息,从而导致虚拟陀螺的精度较低。针对此问题,本文选用时间序列分析中的自回归模型(AR模型)来描述陀螺的内部特征。高阶的自回归模型虽然可以提高预测精度,但是也会极大地增加滤波器的阶数。本文选用一阶AR模型,模型表达式为:
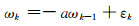
|
(1) |
式中,ωk为陀螺的输入角速度,a为模型系数,εk为方差为q的零均值白噪声。
在陀螺的测试过程中,不可避免地有噪声干扰,MEMS陀螺通常采用的输出模型为[8]:
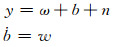
|
(2) |
式中,y为单个陀螺输出信号,b为速率随机游走,即为受随机游走w驱动的噪声,n为角度随机游走。速率随机游走和角度随机游走都是陀螺随机漂移的分量。
为了降低卡尔曼滤波器的维数,需要使用简化的陀螺测量模型。使用动态Allan方差法分析MEMS陀螺输出的随机误差可以发现,MEMS陀螺的随机误差主要由零偏不稳定性和角度随机游走组成,因此可以将测量模型中速率随机游走b省略,从而可以将MEMS陀螺的输出模型简化为:
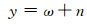
|
(3) |
为了设计卡尔曼滤波器,首先要建立陀螺阵列的状态空间方程和量测方程。选取陀螺阵列的输入角速度为状态量,根据式(1)给出的单个陀螺自回归模型,得到陀螺阵列的状态空间方程为:
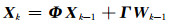
|
(4) |
式中,Xk即为ωk,Φ为-a,Γ为1,Wk-1为系统噪声,且E[Wk]=0, cov[Wk, Wj]=E[WkWjT]=qδkj。
根据式(3)给出的单个陀螺输出模型,可以得到陀螺阵列的量测方程为:

|
(5) |
式中,Zk=[yk1, yk2, …yk6]T为陀螺阵列的输出矩阵,Hk=[1, 1, …1]T为陀螺的量测矩阵,Vk=[nk1, nk2, …nk6]T为陀螺的噪声矩阵,且E[Vk]=0,cov[Vk, Vj]=E[VkVjT]= Rδkj。
由于陀螺矩阵中各陀螺的工艺、材料、环境一致,所以噪声矩阵不是对角矩阵,记陀螺之间的相关性系数为ρij,则R为:

|
(6) |
式中,σ2为角度随机游走的噪声方差。
3 卡尔曼滤波器设计及优化根据状态空间方程(式(4))和量测方程(式(5)),设计如下卡尔曼滤波器。
状态一步预测值为:
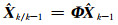
|
(7) |
状态估计值为:
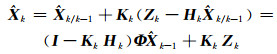
|
(8) |
增益Kk为:
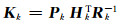
|
(9) |
估计误差方差矩阵Pk为:

|
(10) |
一步预测误差方差阵Pk/k-1为:
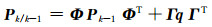
|
(11) |
通过式(7)~(10)设计的卡尔曼滤波器能够从陀螺矩阵的6个输出值中融合出陀螺输入角速度。但此滤波器在每次循环时都需要计算增益Kk、估计误差方差矩阵Pk、一步预测误差方差阵Pk/k-1,使滤波器的实时性受到影响。根据文献[9]可知,虚拟陀螺系统是完全随机可观和完全随机可控的,也就意味着系统是稳定的,那么误差方差矩阵Pk、Pk/k-1和增益Kk都是渐进稳定的而且与初值无关,这3个值会很快地收敛至稳态值。
估计误差方差阵的稳态值Pk可由下式求得:
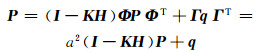
|
(12) |
根据式(9)可以得到增益Kk的稳态值为:
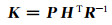
|
(13) |
将式(13)代入式(12)得:
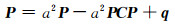
|
(14) |
则有:
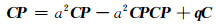
|
(15) |
其中,C=HTR-1H。解式(15)可得:
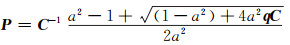
|
(16) |
则增益矩阵的稳态值K为:
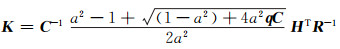
|
(17) |
将式(17)代入式(8)得:
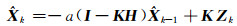
|
(18) |
式(7)和式(18)即为改进后的滤波器,增益K 可根据模型参数、系统误差提前解算,不需要在数据估计的过程中循环计算,极大地节约了每次数据循环的时间,实现了数据融合的实时性。
4 实验设计及数据处理 4.1 陀螺的基本参数测试首先给出陀螺阵列中6个陀螺的排列方式,其实物图如图 1所示。

|
图 1 陀螺阵列实物图 Fig. 1 Practicality picture of gyroscope array |
实验所用陀螺设定的带宽为40 Hz,为满足奈奎斯特定律[7],设定数据采集频率为200 Hz。经测试,MEMS陀螺的角度随机游走方差为0.396 9°/s1/2,角速度方差为9.13×10-9,陀螺的自回归模型中系数a=-0.999 9。经多元分析计算出各陀螺间的Pearson相关系数如表 1所示。
|
|
表 1 各陀螺间的Pearson相关系数 Tab. 1 Pearson correlation coefficient between different gyroscope |
根据表 1给出的各陀螺相关系数就可以写出式(6)给出的R矩阵。
4.2 实验验证分别设计恒速实验和摇摆实验来验证所设计的数据融合方法的有效性。在数据处理过程中,还对随机游走模型和AR模型的数据融合效果进行比较。
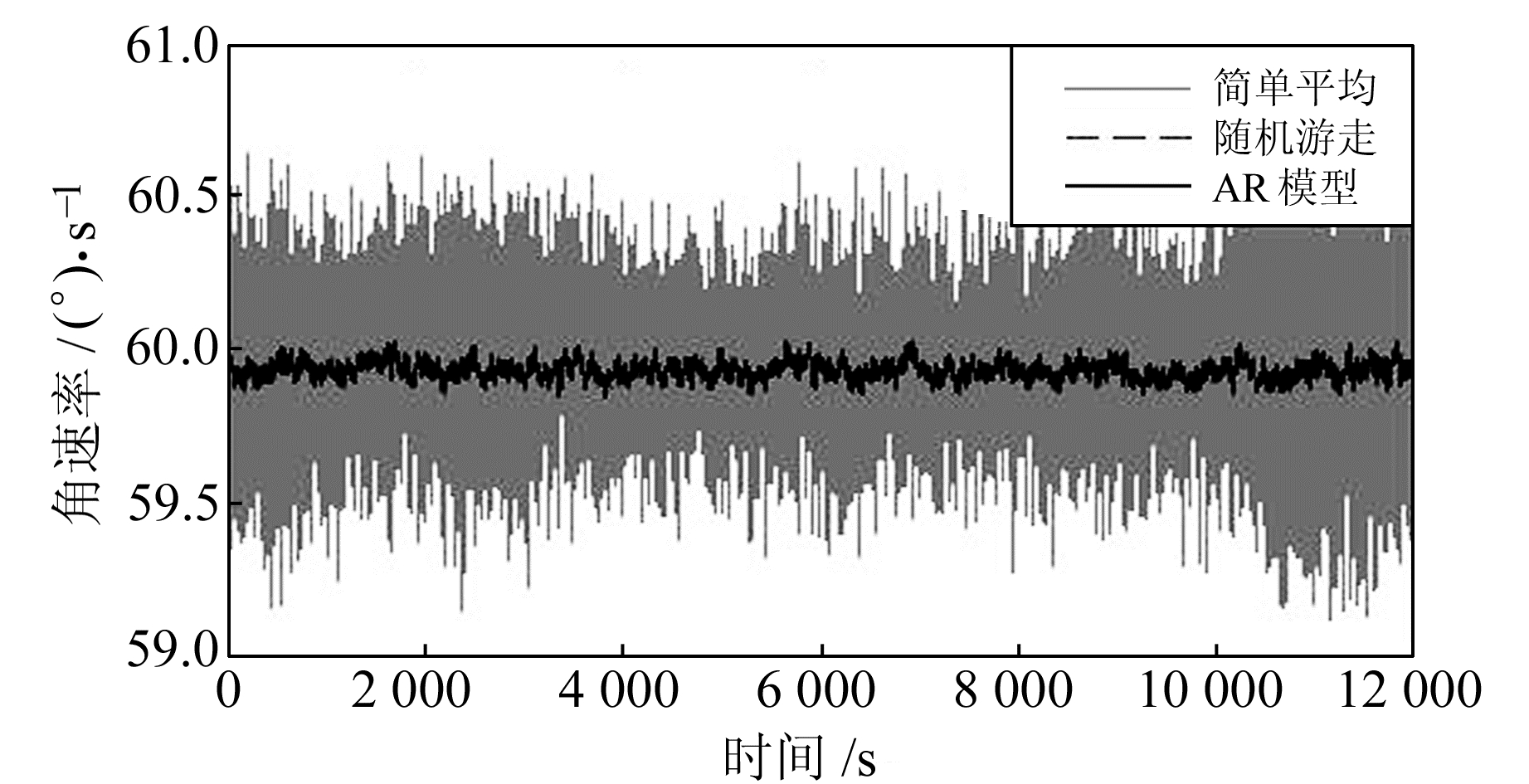
设计恒速实验:将陀螺阵列放在水平转台上,使其输入轴与转台转轴一致。设置转台旋转角速度为60°/s,等陀螺输出稳定后开始采集数据,采集频率为200 Hz,采集时间为12 000 s。对原始数据分别用简单平均、随机游走和AR模型进行处理,其结果如图 2所示。AR模型和随机模型的效果在恒速实验中相近,图形几乎重合。
|
图 2 恒速实验数据处理结果 Fig. 2 Results of data processing under constant speed experiment |
设计摇摆实验:陀螺的放置方式和数据采集的频率、时间不变,将转台角速度设置为正弦函数ω=10×sin(0.21t)(°)/s。对原始数据依然使用简单平均、随机游走和AR模型进行处理,其处理结果如图 3所示。

|
图 3 摇摆实验数据处理结果 Fig. 3 Results of data processing under swing experiment |
3种数据处理方式的输出误差如图 4所示。

|
图 4 输出误差 Fig. 4 The output error |
用1σ标准偏差来衡量陀螺仪精度提高的效果,统计结果如表 2所示。
|
|
表 2 测试结果统计 Tab. 2 Statistics of test results |
从表 2可以看出,使用简单平均进行信息融合时,其标准差相对于单个陀螺降低了约47%,这也符合统计规律;使用随机游走模型进行卡尔曼滤波时,在恒速率实验中其精度提高了17.54倍,但是在摇摆实验中却没有提高,说明随机游走模型描述动态过程时有一定的缺陷;使用AR模型进行卡尔曼滤波时,恒速条件下精度提高了18.18倍,摇摆实验中精度提高了5.36倍,明显高于另外2种数据融合方法,证明了本文建立的模型和设计的滤波器效果明显,能很好地提高陀螺精度。
5 结语本文首先建立单个MEMS陀螺的AR模型和输出模型,然后基于这2个模型给出虚拟陀螺的状态空间方程和量测方程,设计卡尔曼滤波器对陀螺阵列的输出信息进行融合,并优化卡尔曼滤波器来减小数据处理周期,最后设计恒速实验和摇摆实验对本文提出的数据融合方法进行验证。结果表明,本文提出的虚拟陀螺技术可以极大地提高陀螺的测量精度,说明了所建立模型和滤波方法的有效性和优越性。
| [1] |
王浩, 丁炜. MEMS加速度计与传统地震加速度计的比较研究[J]. 大地测量与地球动力学, 2013, 33(增2): 93-95 (Wang Hao, Ding Wei. Comparison among MEMS Accelerometer and Traditional Seismometer[J]. Journal of Geodesy and Geodynamics, 2013, 33(Supp2): 93-95)
(  0) 0) |
| [2] |
王伟, 杜东贞, 周佳欣, 等. MEMS三轴陀螺仪中不匹配干扰抑制方法[J]. 系统工程与电子技术, 2016, 38(7): 1638-1643 (Wang Wei, Du Dongzhen, Zhou Jiaxin, et al. Control Method of Mismatched Disturbances for MEMS Triaxial Gyroscope[J]. Systems Engineering and Electronics, 2016, 38(7): 1638-1643)
(  0) 0) |
| [3] |
吴焕铭, 尹韬, 杨海钢, 等. 基于双通道解调相位校准技术的MEMS陀螺仪接口电路芯片[J]. 中国惯性技术学报, 2015, 23(6): 805-811 (Wu Huanming, Yin Tao, Yang Haigang. MEMS Gyroscope Interface Circuit on Chip Based on Dual-Channel Demodulation Phase Calibration Technique[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 805-811)
(  0) 0) |
| [4] |
王昊, 王俊璞, 田薇风, 等. 梯度RBF神经网络在MEMS陀螺仪随机漂移建模中的应用[J]. 中国惯性技术学报, 2006, 14(4): 44-48 (Wang Hao, Wang Junpu, Tian Weifeng, et al. Application of Gradient Radial Basis Function Network in the Modeling of MEMS Gyro's Random Drift[J]. Journal of Chinese Inertial Technology, 2006, 14(4): 44-48 DOI:10.3969/j.issn.1005-6734.2006.04.010)
(  0) 0) |
| [5] |
赵世峰, 张海, 范耀祖. MEMS陀螺随机漂移多尺度滤波方法[J]. 中国惯性技术学报, 2007, 15(2): 229-232 (Zhao Shifeng, Zhang Hai, Fan Yaozu. Multiscale Filtering Methods for MEMS Gyros Random Drift[J]. Journal of Chinese Inertial Technology, 2007, 15(2): 229-232 DOI:10.3969/j.issn.1005-6734.2007.02.026)
(  0) 0) |
| [6] |
杨金显, 袁赣南, 周卫东. 基于局域波分解的微机械陀螺信号提取研究[J]. 宇航学报, 2008, 29(4): 1341-1344 (Yang Jinxian, Yuan Gannan, Zhou Weidong. Micro-Mechanical Gyro Signal Stripping Based on Local-Wave Decomposition[J]. Journal of Astronautics, 2008, 29(4): 1341-1344 DOI:10.3873/j.issn.1000-1328.2008.04.046)
(  0) 0) |
| [7] |
卢海曦, 夏敦柱, 周百令. 基于遗传小波神经网络的MEMS陀螺误差建模[J]. 中国惯性技术学报, 2008, 16(2): 216-219 (Lu Haixi, Xia Dunzhu, Zhou Bailing. MEMS Gyroscope's Error Modeling Based on Wavelet Neural Network of Genetic Algorithms[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 216-219)
(  0) 0) |
| [8] |
Xue L, Jiang C Y, Chang H L, et al. A Novel Kalman Filter for Combining Outputs of MEMS Gyroscope Array[J]. Measurement, 2012, 45(4): 745-754 DOI:10.1016/j.measurement.2011.12.016
(  0) 0) |
| [9] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1988 (Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Therory of Kalman Filter and Integrated Navigation[M]. Xi'an: Northwestern Polytechnical University Press, 1988)
(  0) 0) |
| [10] |
Derfee D S, Shaham Y K, Kasevich M A. Long-Term Stability of an Area-Reversible Atom-Interferometer Sagnac Gyroscope[J]. Physical Review Letters, 2006, 97(24): 387-392
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37



