2. 内蒙古赤峰地质矿产勘查开发院,赤峰市临潢大街,024005
符合设计要求的轨道几何参数是保障无砟轨道平顺性的基础[1]。通常采用静态检测来获取轨道的几何状态参数,即采用轨道检测小车对高铁线路的几何状态参数进行检测[2]。为了保证轨道检测数据的精准性,必须有效剔除其中可能存在的粗差,且最好能够自动处理。
轨道检测数据的去噪通常以傅里叶变换为基础[3],但这种方法对信号的保护不能顾全所有的离散数据,信号保护与噪声抑制存在矛盾,高频轨道检测数据中有用部分与噪声不能区别,不能描述轨道检测数据信号的局部特性,使数据误差有较大的不确定性。小波变换可以有效分离原始轨道检测数据高频部分的有用信号及噪声,同时可以相对准确地剔除数据中的噪声干扰,较大程度地减小粗大误差对轨道检测数据的影响,更适合分析及去除离散突变信号中的粗大误差[4]。
1 高铁无砟轨道静态检测方法我国现行的高铁轨道几何状态参数检测项包括轨道的轨向、中线和轨面高程、超高、轨距[5]。通过对比检测数据与设计值的差值,可以对高铁线路质量进行判断。
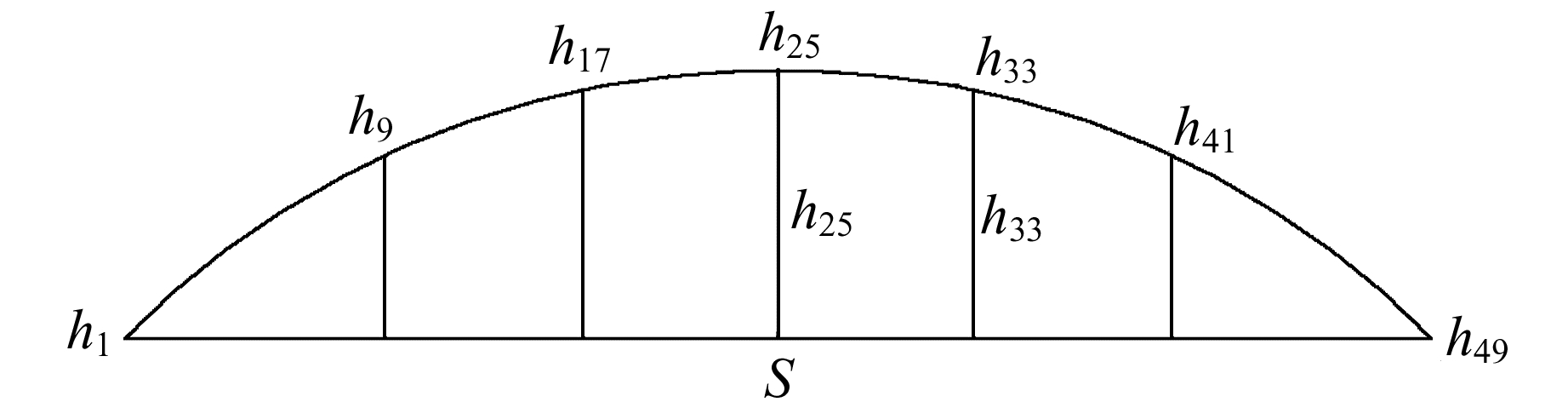
1) 轨向。我国钢轨轨枕间距为0.625 m,因此在30 m短弦检测方法中,每间距8倍的距离设置一对检测点,见图 1。
|
图 1 30 m短弦检测示意图 Fig. 1 30 m chord detection |
轨向检测计算公式为:

|
(1) |
2) 中线和轨面高程。通过检测钢轨轨枕的坐标及高程,然后与设计值进行对比,得出轨道中线及轨面高程的偏差,见图 2。
|
图 2 中线检测原理示意图 Fig. 2 Principle of midline detection |
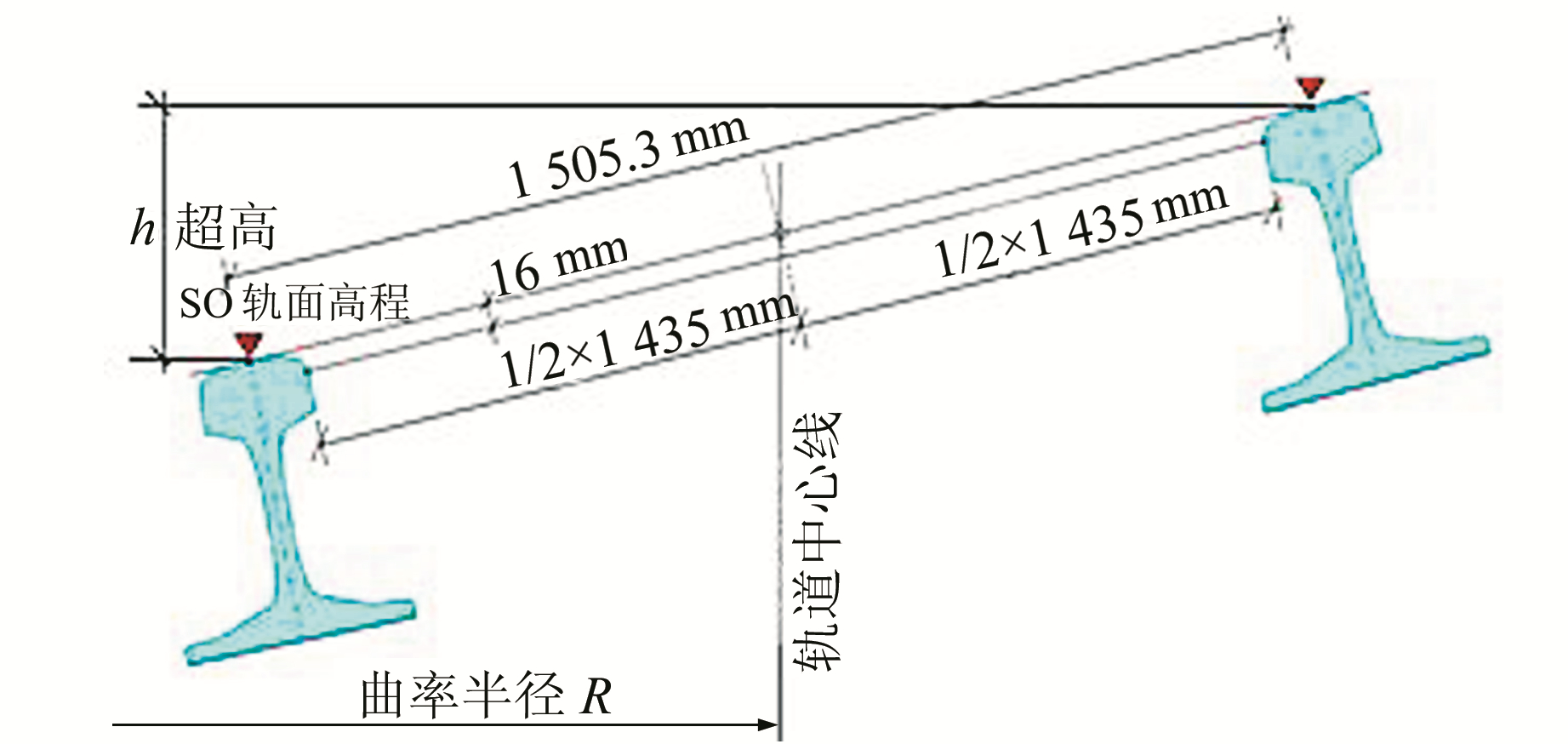
3) 超高。轨道超高是指钢轨表面中心所在直线在竖直面内的高度偏差[6]。将实测的超高数据与设计值对比,即可得到钢轨的超高偏差值[7],见图 3。
|
图 3 超高测量示意图 Fig. 3 Superelevation measurement |
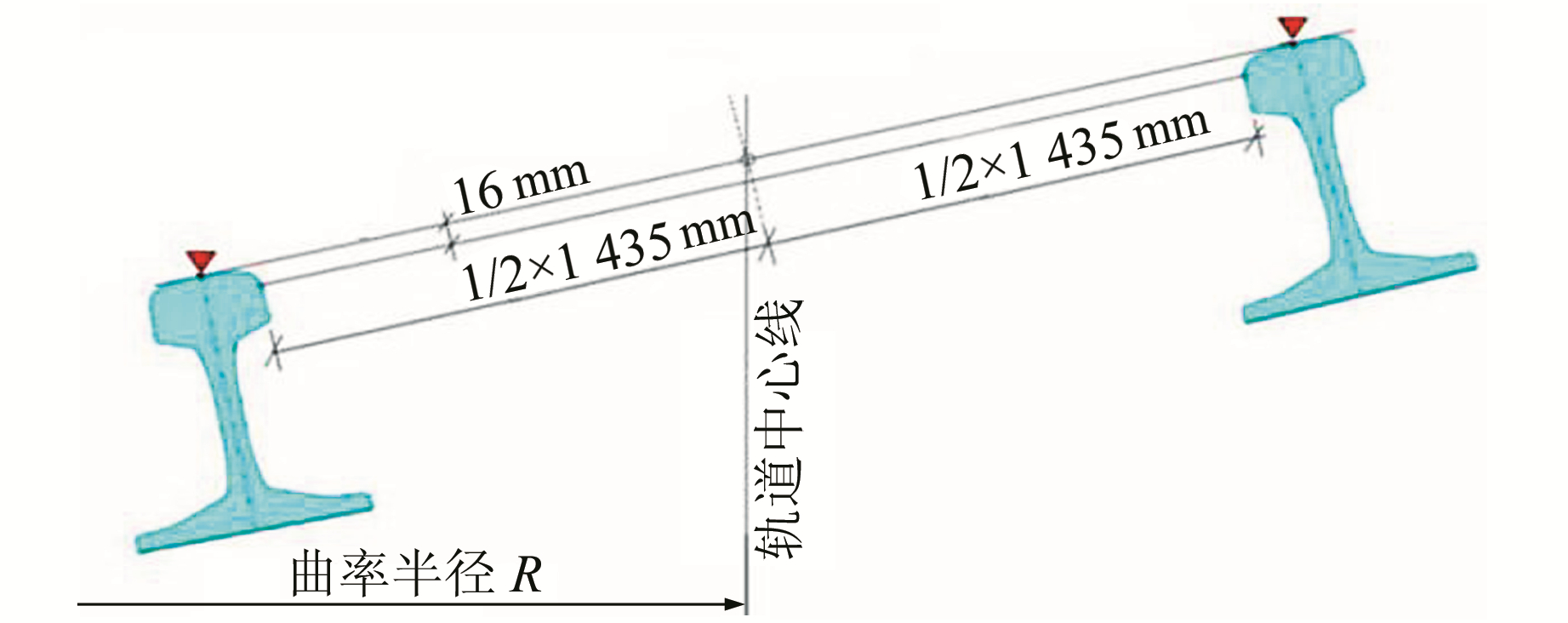
4) 轨距。我国现行的轨距标准值为1 435 mm,误差不超过±1 mm,轨距变化率不超过1 mm/1.5 m[8],见图 4。
|
图 4 轨距检测示意图 Fig. 4 Track gauge measurement |
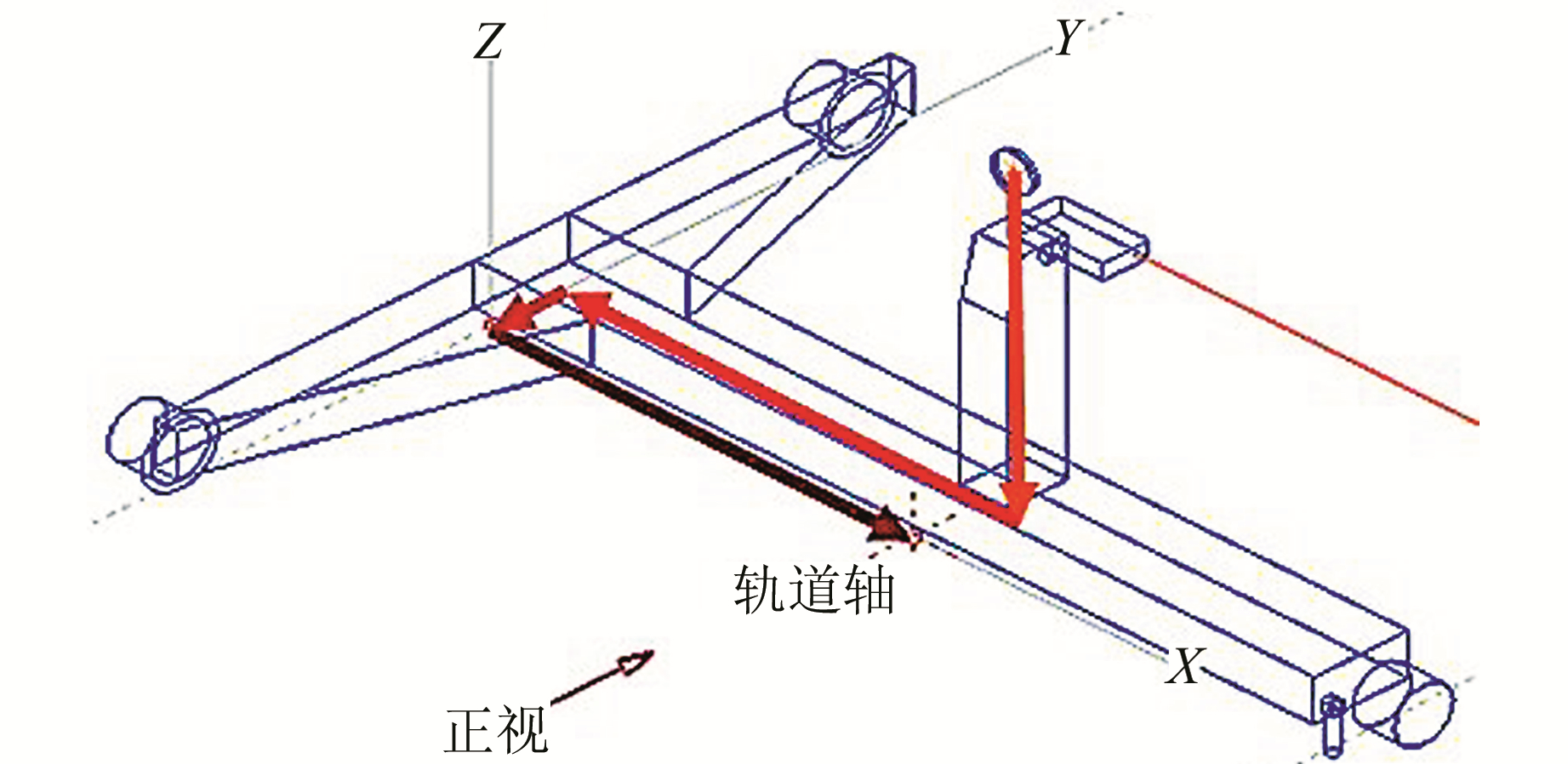
静态检测系统主要由轨道检测小车、高精度全站仪以及外业数据采集软件、内业数据处理软件等组成。全站仪通过6~8个控制点(CPⅢ)自由设站。通过检测轨检小车棱镜,得到该轨枕点的绝对坐标。通过小车搭配的传感器,计算得到轨道几何参数的相对数据。将得到的轨道几何状态参数实时地通过手簿软件解算,就可以得到实测数据与设计值的差值,从而指导高铁无砟轨道的长轨精调以及道岔的安装调整[9],见图 5。

|
图 5 轨检小车检测原理 Fig. 5 Detection principle of track geometry inspection car |
ψ(t)是一个平方可积的函数,如果ψ(t)的傅里叶变换ψ(ω)满足
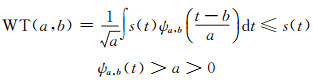
|
(2) |
式中, a为尺度因子,b为平移因子。为方便计算,需要对尺度因子a和连续的平移因子b进行离散化处理。对其进行二进制动态采样,a0=2, b0=1,得到二进制小波变换:
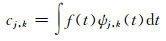
|
(3) |
式中,
轨道检测信号模型可表示为:

|
(4) |
式中,f(i)为真实信号, e(i)为噪声, s(i)为含噪声的信号, ε为噪声水平系数。
对轨道原始检测数据进行三尺度分解,见图 6,图中,cAi表示低频信号,cDi表示高频信号。轨道检测数据属于离散信号,轨道检测信号中的重要数据信息包含在低频部分,而粗差噪声主要包含在高频部分。所以,对小波分析后的高频信号进行降噪处理,可以剔除轨道检测数据中的粗差。

|
图 6 三尺度小波分解 Fig. 6 Three-scale wavelet decomposition |
采用3σ准则对数据中的粗差点进行判断,然后将检测数据进行滤波处理,就可以实现原始轨道检测数据中粗大误差的处理。3σ准则即对于某一个可疑数据xd,若

|
(5) |
则认为xd中含有粗差,这个数据已经失去真实性,可以将其剔除,或者对这个数据进行改正。
2.2 小波基选择对高铁无砟轨道静态检测数据信号进行分解,要求使用正则性比较好的小波基,本文使用Daubechies小波系。对外轨超高检测原始数据进行db1小波的三尺度分析,见图 7。图中,s表示轨道检测数据的原始数据信号,a3表示小波分析的第三层近似,d3表示小波分析的第三层细节,d2表示小波分析的第二层细节,d1表示小波分析的第一层细节(s即为图 6中的X,di即为图 6中的cDi)。

|
图 7 轨道检测超高信号的db1小波三层分解 Fig. 7 Three-scale decomposition of db1 wavelet for superelevation measurement signal |
对轨道检测数据进行分析,首先要选择dbN小波的序号。对高铁轨道检测超高数据进行小波分析,得到db1、db2和db3小波基分解的高频部分,形成的高频信号见图 8。可以看出,随着序号N的增加,数据的突变区间逐渐变大,轨检数据的振幅逐渐变小,db1小波基相对于其他序号的小波基的脉冲区间清晰明显。

|
图 8 超高数据db1-3小波三尺度分解高频部分 Fig. 8 High frequency of three-scale decomposition of db1-3 wavelet for superelevation measurement signal |
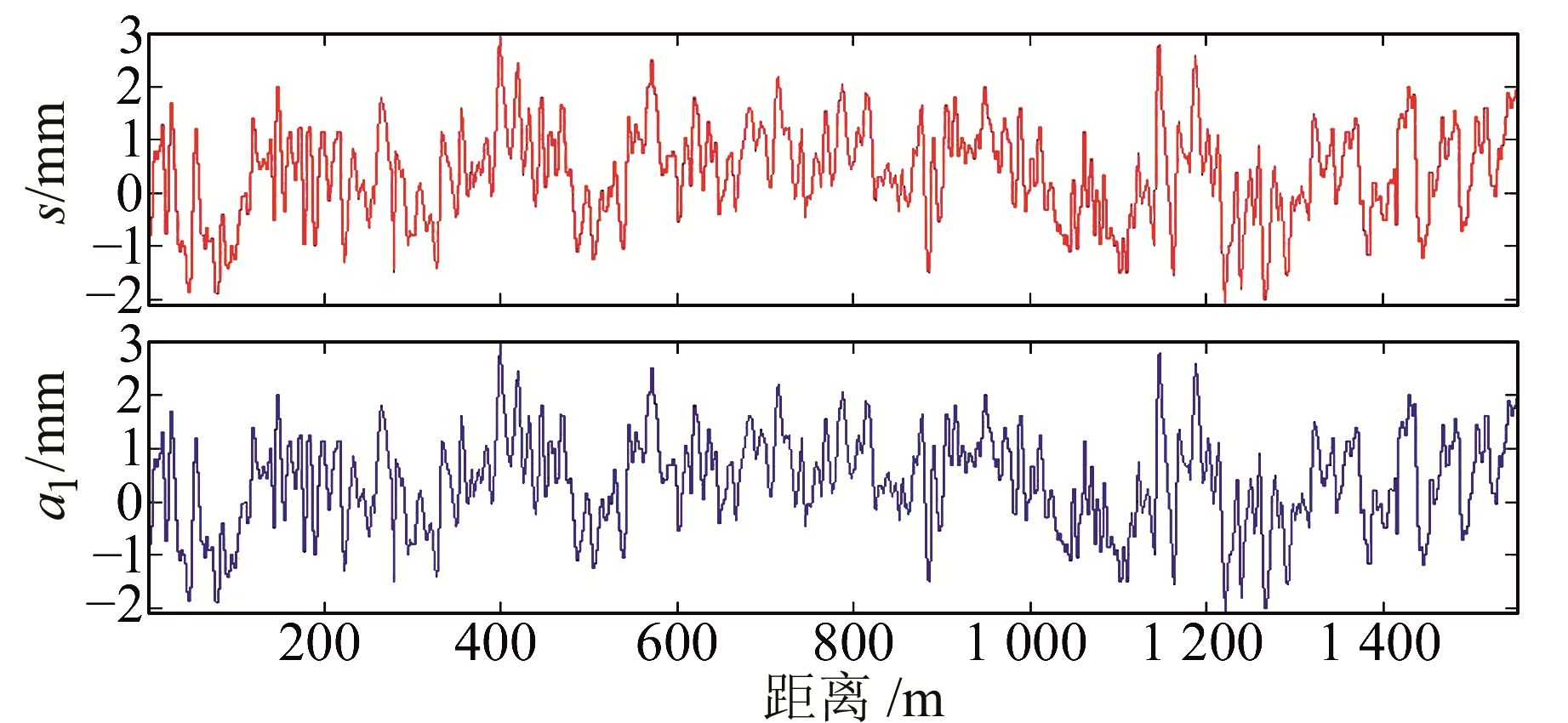
采用db1小波基对采集的轨道超高数据信号进行单尺度、双尺度以及三尺度分解,得到的信号见图 9~11。
|
图 9 轨道超高单尺度分解 Fig. 9 Single-scale wavelet decomposition for superelevation measurement signal |
|
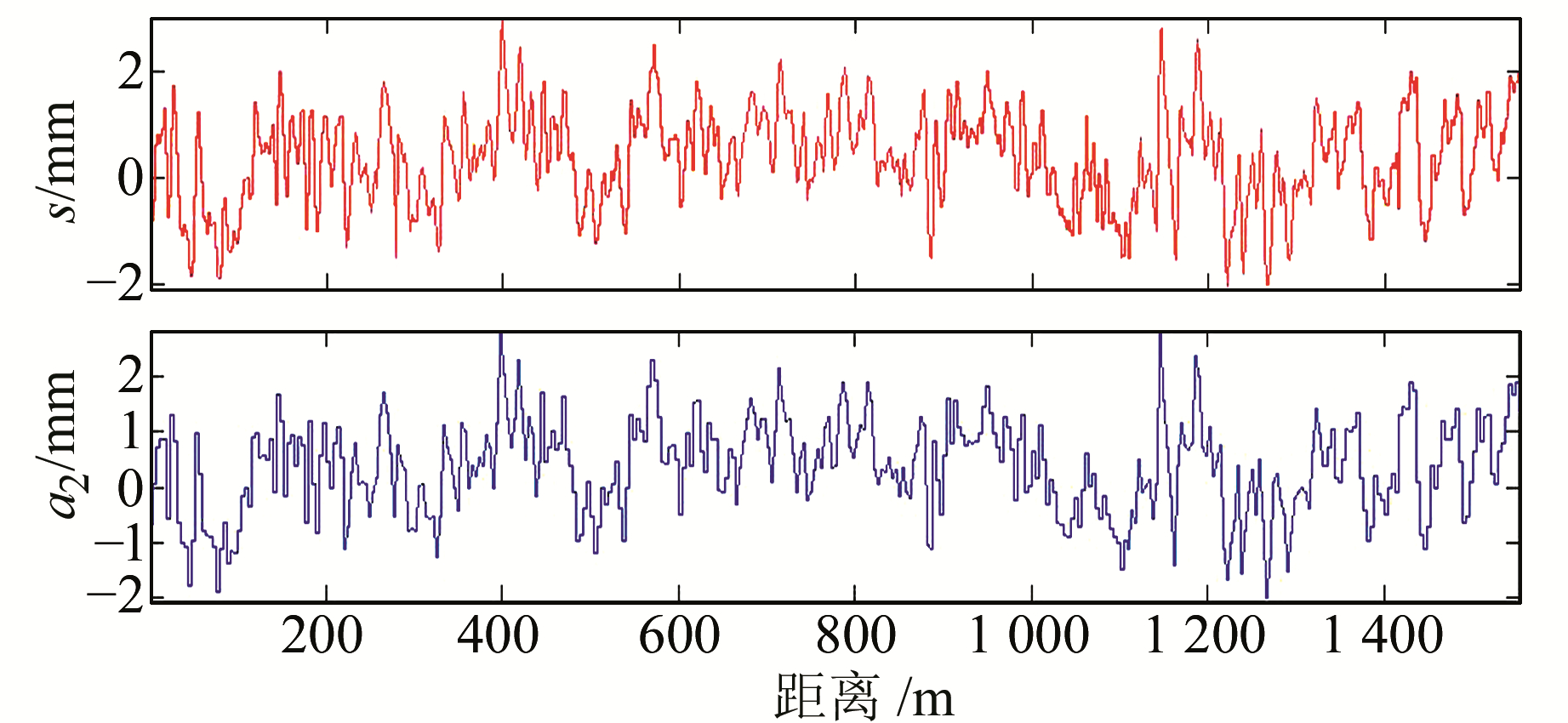
图 10 轨道超高双尺度分解 Fig. 10 Two-scale wavelet decomposition for superelevation measurement signal |
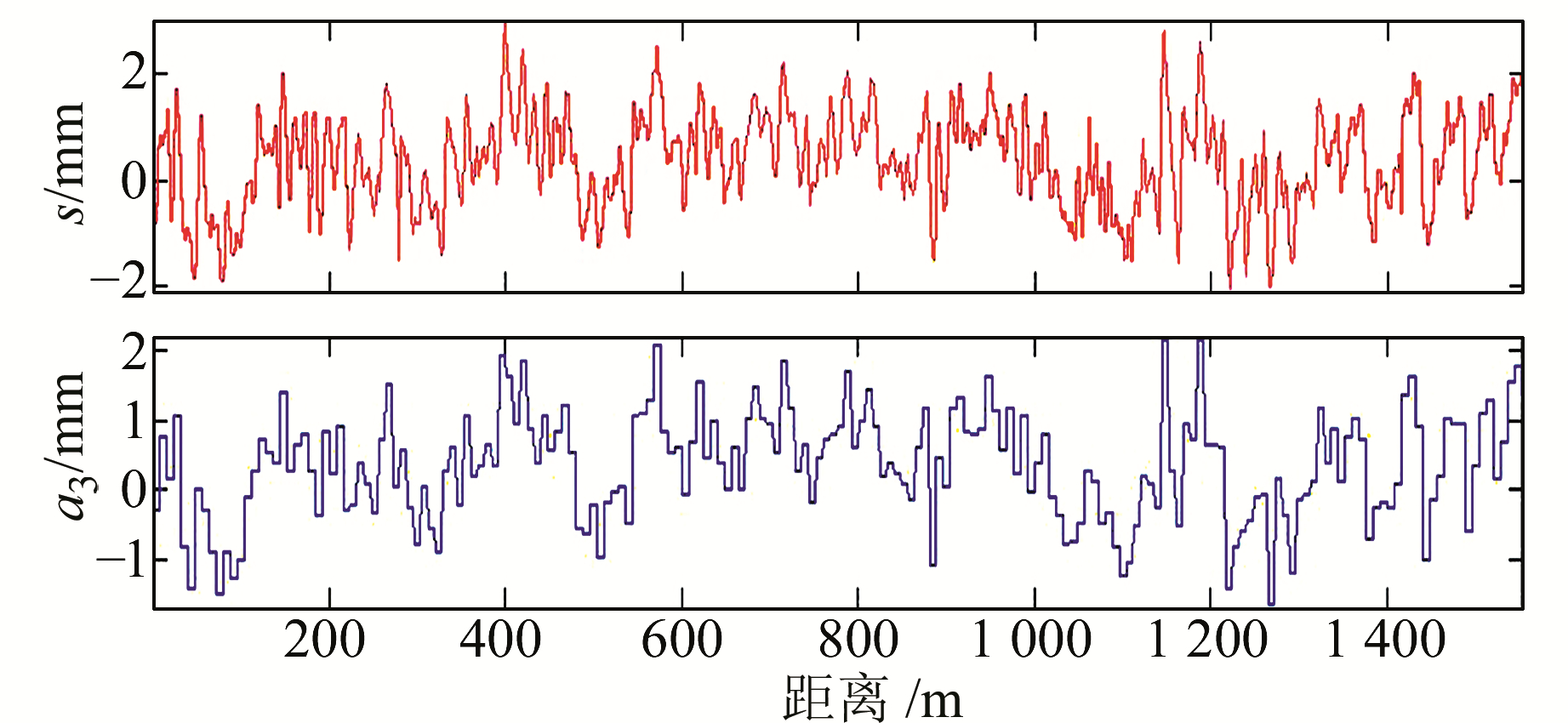
|
图 11 轨道超高三尺度分解 Fig. 11 Three-scale wavelet decomposition for superelevation measurement signal |
利用均方误差(RMSE)、信噪比(SNR)、平滑度(r)3个指标对Daubechies小波的db1、db2和db3小波基进行分析,得到超高数据去噪的指标值,结果见表 1。由表 1可知,随着Daubechies小波系中序号N的增加,均方误差RMSE越来越大,信噪比SNR越来越小,平滑度r越来越小。相对而言,db1小波比其他序号小波的滤波效果要好。
|
|
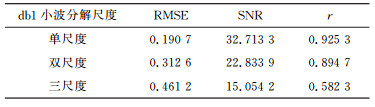
表 1 轨道超高检测数据不同小波三尺度分解指标 Tab. 1 Index of three-scale wavelet decomposition for superelevation measurement data |
利用db1小波进行信号的单尺度、双尺度以及三尺度分解,得到各分解尺度的去噪指标,见表 2。可以看到,随着分解尺度的增加,均方误差RMSE越来越大,信噪比SNR和平滑度r越来越小。相对而言,db1小波的单尺度分解比其他尺度小波的滤波效果要好。
|
|
表 2 轨道超高检测数据db1小波的不同尺度分解指标 Tab. 2 Index of three-scale decomposition of db1 wavelet for superelevation measurement data |
2015-06利用轨检小车对贵广高铁龙额县一段长约1 500 m的轨道进行检测。根据经验及查阅相关文献发现,轨道检测数据存在粗大噪声干扰,会对轨道平顺性评价带来严重影响。产生粗大噪声的原因主要有:轨道面存在的杂物、隧道中的雾气、大气折射、全站仪照射小车棱镜时错误地照到CPⅢ控制点的棱镜等。根据3σ准则对轨道静态检测数据进行db1小波的单尺度分解,得到检测数据在粗差去噪前后的对比图。
1) 高程数据。图 12为轨道高程检测原始数据。由图可见,轨道的高程检测原始数据中存在突变点(红线),通过小波去噪(蓝线),突变点被消除。

|
图 12 高程预处理结果 Fig. 12 Pretreatment results of elevation data |
2) 轨向数据。图 13为轨道轨向检测原始数据。可以看出,轨向检测原始数据中不存在突变点。仍采用小波分析对检测数据进行粗差处理,发现数据处理对原始数据无影响,无数据丢失。可以判断,本文提出的滤波去噪方法对有效数据无删减丢失现象。

|
图 13 轨向预处理结果 Fig. 13 Pretreatment results of alignment data |
3) 超高数据。图 14为轨道外轨超高检测原始数据。可以看出,所采集的数据存在突变点(红线)。小波去噪后得到较好的检测数据(蓝线),突变点被消除。

|
图 14 超高预处理结果 Fig. 14 reprocessing results of superelevation measurement data |
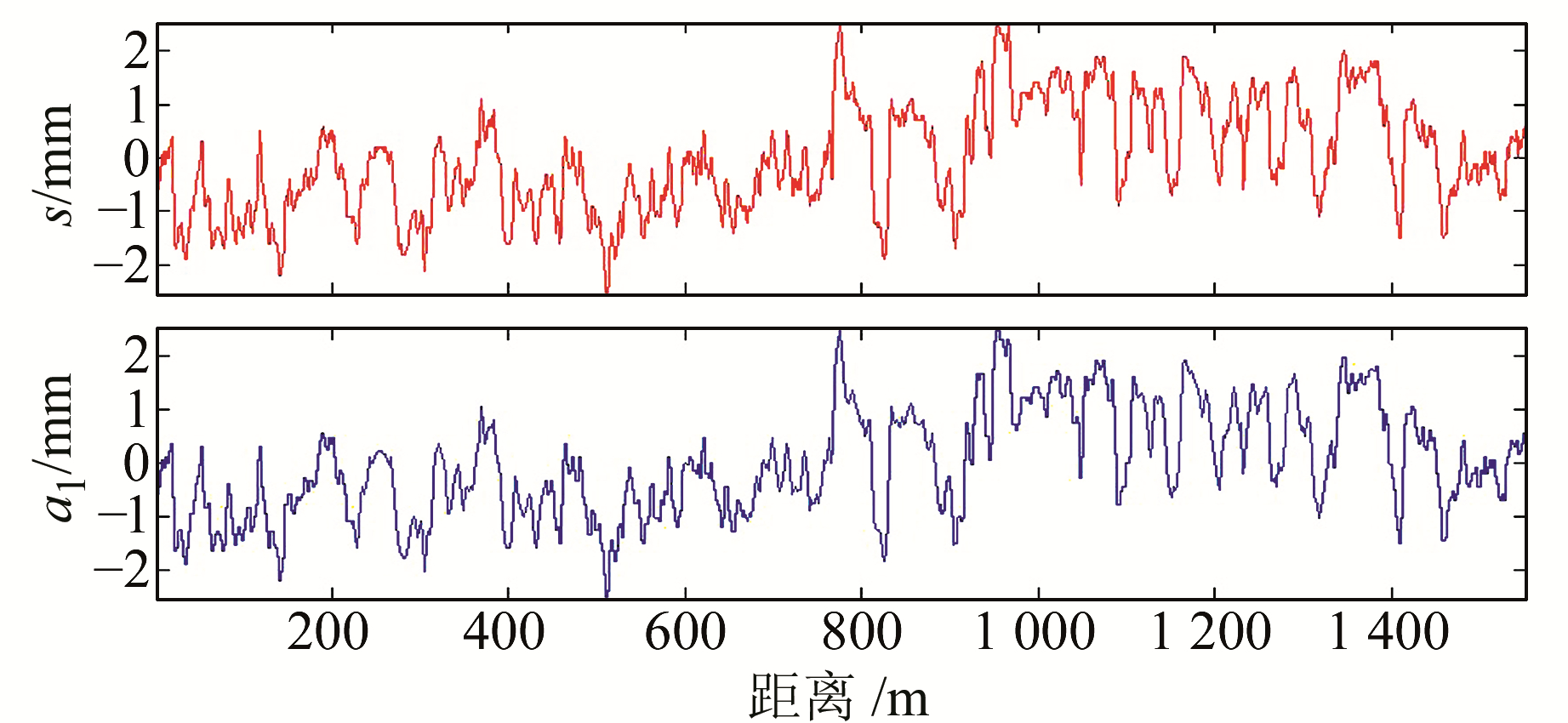
4) 轨距数据。图 15为轨道轨距检测原始数据。可以看出,轨道的轨距检测数据中不存在突变点。仍采用小波分析对检测数据进行粗差处理,发现数据处理对原始数据无影响、无数据丢失。
|
图 15 轨距预处理结果 Fig. 15 Pretreatment results of track gauge data |
从上面的分析可以看出,数据信号的噪声影响主要包含在轨道静态检测数据的高频部分。所以,对信号的高频部分采用3σ准则进行阈值去噪处理,可以有效剔除检测数据中存在的粗差。通过选择不同的小波基处理发现,db1小波基的单层分解最适合轨道检测数据的去噪处理。将剔除粗差后的数据导入平顺性评价系统GEDO LRA,见图 16。图中的图形和数据充分说明了数据处理方案的准确性和有效性。

|
图 16 小波去噪后数据导入平顺性评价系统成果 Fig. 16 The wavelet denoising results data import quality evaluation system |
利用3σ准则及小波分析对轨道静态检测的原始数据进行处理,可以有效去除数据中存在的粗差。对于不存在粗差的轨检数据,小波分析没有对原始数据进行任何改变,验证了小波分析在轨检数据粗差处理中的有效性。另外,将处理后的数据导入平顺性评价系统GEDO LRA的计算结果,也验证了数据处理方案的正确性。
| [1] |
刘世海, 郭建钢, 王波. CRTSⅠ型双块式无砟轨道静态调整和动态调整技术[J]. 铁道标准设计, 2010, 1(6): 80-84 (Liu Shihai, Guo Jiangang, Wang Bo. CRTS Ⅰ Double-Block-Free Fragments Track Static and Dynamic Adjustment Techniques to Adjust[J]. Railway Standard Design, 2010, 1(6): 80-84)
(  0) 0) |
| [2] |
郝亚东, 赵杰, 樊廷春. 基于GRP1000的无砟轨道精调测量研究[J]. 测绘通报, 2013(4): 52-55 (Hao Yadong, Zhao Jie, Fan Tingchun. Study of Non-Ballasted Track Fine-Tuning Measurement Based on GRP1000[J]. Bulletin of Surveying and Mapping, 2013(4): 52-55)
(  0) 0) |
| [3] |
李智强, 李天瑞. 小波阈值去噪在动车组数据处理中的应用[J]. 计算机工程, 2011(21): 235-237 (Li Zhiqiang, Li Tianrui. Application of Wavelet Threshold Denoising in CRH Train Data Processing[J]. Computer Engineering, 2011(21): 235-237)
(  0) 0) |
| [4] |
陈宪麦, 王澜, 陶夏新, 等. 基于小波分析理论的轨道不平顺分析[J]. 铁道工程学报, 2008, 25(1): 57-61 (Chen Xianmai, Wang Lan, Tao Xiaxin, et al. Analysis of Track Irregularity with Wavelets Analysis Theory[J]. Journal of Railway Science and Engineering, 2008, 25(1): 57-61 DOI:10.3969/j.issn.1006-2106.2008.01.012)
(  0) 0) |
| [5] |
杨成宽. GEDOCE轨道检测系统在无砟轨道施工测量中的应用[J]. 铁道工程学报, 2009, 26(3): 57-61 (Yang Chengkuan. Application of GEDOCE Track Detection System in Slab Track Construction[J]. Journal of Railway Science and Engineering, 2009, 26(3): 57-61 DOI:10.3969/j.issn.1006-2106.2009.03.013)
(  0) 0) |
| [6] |
胡庆丰, 安博格. GRP1000轨检小车进行无砟碴轨道检测的作业方法[J]. 铁道勘察, 2008(3): 17-20 (Hu Qingfeng, An Boge. Operational Method for Checking Ballastless Track with GRP1000 Track Checking Car Made by Amberg Technology AG[J]. Railway Investigation and Surveying, 2008(3): 17-20 DOI:10.3969/j.issn.1672-7479.2008.03.006)
(  0) 0) |
| [7] |
陈宪麦.轨道不平顺时频域分析及预测方法的研究[D].北京: 铁道部科学研究院, 2006 (Chen Xianmai.Time-Frequence Analysis and Prediction Study on Track Irregularities[D].Beijing: Academy of Railway Sciences, 2006)
(  0) 0) |
| [8] |
于朝旭.无砟轨道施工测量关键技术应用与探讨[D].阜新: 辽宁工程技术大学, 2013 (Yu Chaoxu.The Discussion and Application of Ballastless Track Construction Measurement Key Technology[D].Fuxin: Liaoning Technical University, 2013)
(  0) 0) |
| [9] |
黄旭东, 刘光斌, 王德佳. GEDOCE轨道精调系统在高铁测量中的应用[J]. 煤炭工程, 2012, 32: 161-163 (Huang Xudong, Liu Guangbin, Wang Dejia. Application of GEDOCE Track Fine Tuning System in High Speed Railway Survey[J]. Coal Engineering, 2012, 32(Supp2): 161-163)
(  0) 0) |
| [10] |
杜鹤亭. 长波长轨道不平顺检测中的数字滤波方法[J]. 中国铁道科学, 2000(4): 60-67 (Du Heting. Digital Filtering Method for Long Wavelength Track Irregularity Detection[J]. China Railway Science, 2000(4): 60-67)
(  0) 0) |
2. Inner Mongolia Chifeng Institute of Geology and Mineral Exploration and Development, Linhuang Street, Chifeng 024005, China
 2017, Vol. 37
2017, Vol. 37