2. 中国科学院行星科学重点实验室,上海市南丹路80号,200030;
3. 上海大学通信与信息工程学院, 上海市上大路99号, 200444;
4. 中国地震局地震预测研究所,北京市复兴路63号,100036
目前针对GNSS-R土壤水分监测和定量反演方面的研究主要是利用导航卫星直射信号和反射信号的干涉波形图进行分析。有学者[1]采用专门研制的地基接收机的直射和反射信号形成相干波形,利用波形中凹槽(notch,即波形中反射率最低点)个数、位置信息反演地物参数,取得了良好的反演精度:裸土区土壤水分反演精度为3%~4%,小麦和大麦覆盖区土壤水分反演精度为2%~5%,植被高度反演精度(RMSE)为3~5 cm。Larson和Small等[2-3]提出,可以用地球物理学/大地测量学上的接收机对土壤水分和植被参数进行研究,即利用GPS的多路径数据。研究表明,GPS多路径数据的有效反射计高度、幅度和多路径相位与土壤水分、植被生物物理参数有关,可以利用其对相应参数进行反演[4-5]。国内学者[6-7]利用SMEX观测数据进行了针对性研究,并利用GPS-IR遥感对植被含水量进行遥感分析。
现有研究多是依赖于地面观测数据,建立GNSS-R信号或者GPS多路径信号与土壤水分和植被参数的相关性或建立区域性的定量反演算法,但对其散射特性机理模型的研究相对较少。本文以海洋表面GPS散射信号模型为基础,采用粗糙度范围连续并且能在一个很宽的地表粗糙度范围内再现随机粗糙面散射特性的高级积分方程模型AIEM(advanced integral equation model)来计算裸土的双站雷达散射截面[8],模拟分析裸土参数(土壤水分和地表粗糙度)对接收机DDM的影响。
1 理论方法本文以海洋表面GPS散射信号模型Z-V(其本质上为双站雷达的积分形式[9])为基础,通过对其进行修改,对裸土GPS散射信号波形图进行模拟分析。
1.1 雷达散射截面GPS散射信号模型中,海洋表面针对双站雷达散射界面的计算方法为:

|
(1) |
式中,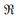
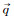

Masters[10]将Z-V模型应用到陆面土壤水分的研究上,其地表散射系数计算采用GO(geophysical optics model)模型,但该模型适用范围有限——粗糙度在水平方向上,相关长度必须大于电磁波波长,垂直方向均方根高度必须足够小。但实际地表的粗糙度情况是连续变化的,因此,针对实际应用需要,应采用粗糙度范围连续变化的地表面散射模型进行计算。
裸土的雷达散射截面计算分为相干和非相干两部分。其中相干部分的计算采用Fung等[11]的相干雷达散射截面的公式进行计算。由于实际地表为随机粗糙表面,入射的导航卫星信号经地表散射后,散射能量中非相干部分的能量不可忽视。常用的随机粗糙地表的面散射模型有KA模型(kirchhoff approach)、SPM模型(small perturbation method)、IEM模型(integrated equation model)以及后来进一步改进的AIEM模型(advanced integrated equation model)[8]。本文采用AIEM模型计算非相干部分的散射。AIEM模型的基本形式可以概括为3项之和:基尔霍夫项σrtk、基尔霍夫补偿项σrtc和二者的交叉项σrtkc,即
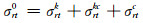
|
(2) |
式中,r、t分别为接收和发射时的极化状态。
对于传统的发射率和后向散射模型,模型计算的为线极化发射率或雷达后向散射截面。而针对GNSS-R遥感来说,本研究采用极化合成的方法计算各种极化雷达散射截面。
1.2 裸土GPS散射信号模型框架裸土GPS散射信号模型中,在观测几何模块、GPS轨道数据库中得到相应的观测角度和频段信息以及发射机、接收机位置/速度信息,用以计算地表镜像点、多普勒等值区和环形区(距离等值线区)。将裸土参数和观测几何信息输入到随机粗糙面散射模型中,计算各种极化的裸土双站雷达散射截面。将上述信息输入到基于Z-V模型的裸土GPS散射信号模型中,得到裸土的延迟多普勒图,进而可以利用该模型模拟分析裸土参数对DDM波形图的影响。该模型可以模拟分析任意观测几何下任意极化的裸土DDM波形。
2 模拟结果根据上述思想建立基于Z-V模型的裸土GPS散射信号模型,模拟分析不同极化和地表参数(地表粗糙度、土壤水分)对DDM波形的影响。模型的输入参数设置如下:GPS频率为fre=1.575 GHz (GPS L1),土壤块密度为bd=1.6,土壤质地中沙土含量为51.5%,粘土含量为13.5%,土壤温度为ts=25 ℃,入射角度为13°,各个地表散射单元的散射天顶角为-50°~50°,散射方位角为-90°~90°,散射角度间隔为5°。在模拟分析中,保持发射机、接收机位置/速度矢量不变,只模拟分析极化和裸土参数变化对DDM波形的影响。
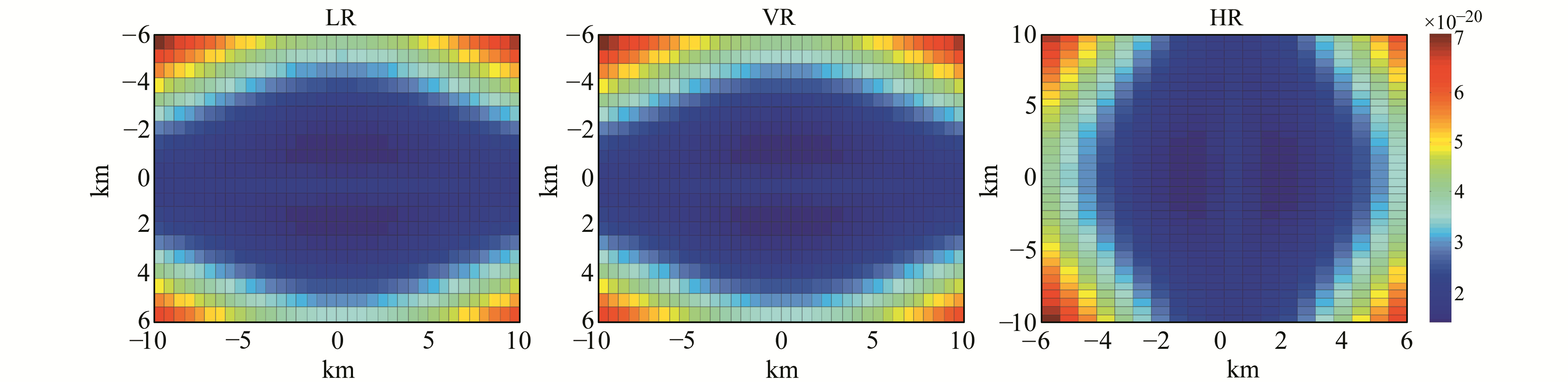
2.1 圆极化多极化双站雷达散射截面在环形区和多普勒等值区域保持不变的情况下,固定土壤含水量为0.1,地表均方根高度为0.1 cm,相关长度为10 cm。图 1模拟了RR、LR、VR和HR极化时,在本地坐标系下各种极化的双站雷达散射截面。从图 1可以看到,RR极化和其余3种极化双站雷达散射截面差别较大,RR极化时,NRCS的值最小。
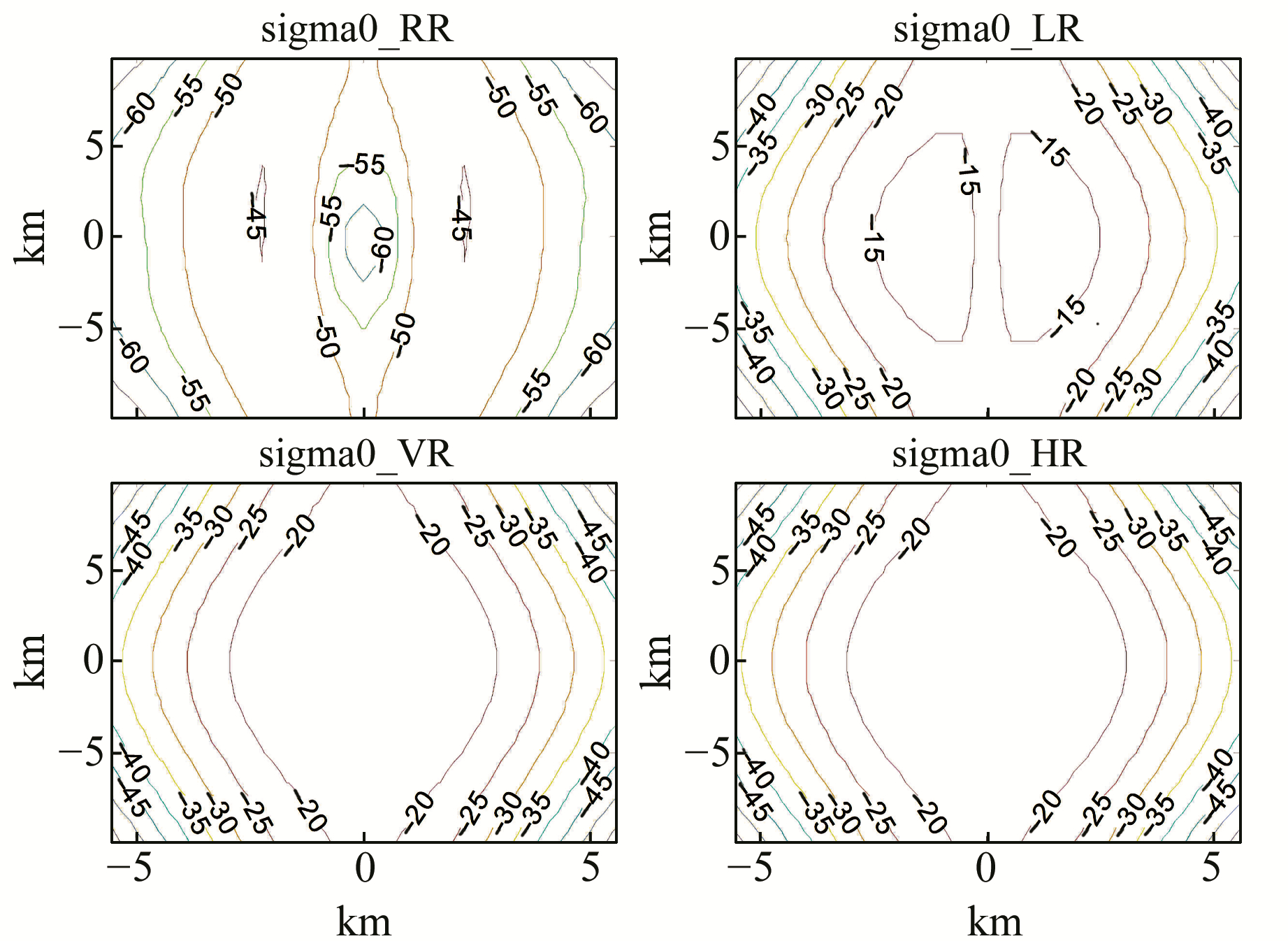
|
图 1 RR、LR、VR和HR极化时裸土的双站雷达散射截面 Fig. 1 Bistatic radar cross section for RR, LR, VR and HR pol |
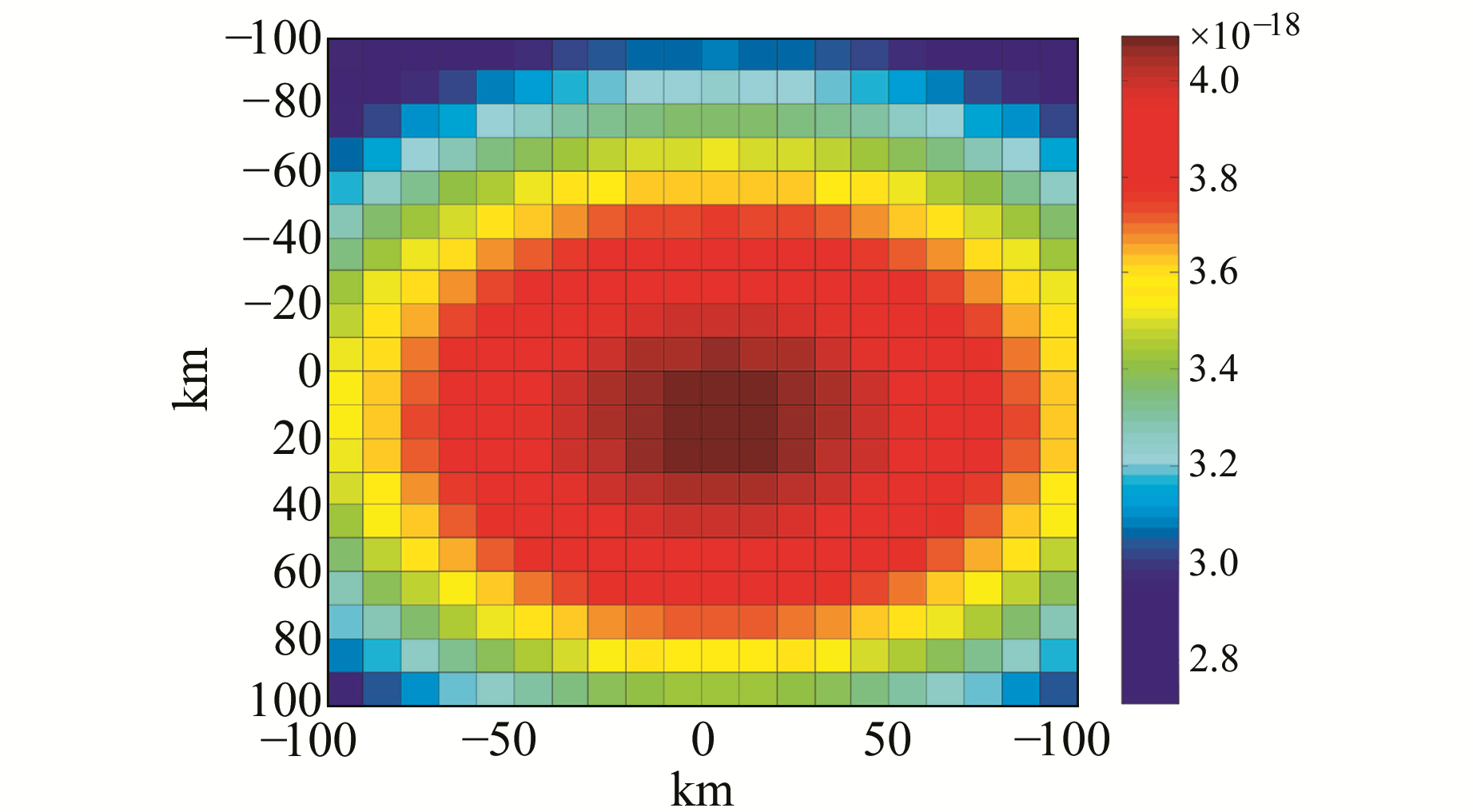
在导航卫星、GNSS-R接收机位置/速度矢量相同情况下,图 2为海洋表面的GPS散射信号能量图,图 3为裸土的RR极化DDM波形图。与图 2相比可以看出,陆面裸土的GPS散射信号能量幅值较海洋表面的小2个数量级。
|
图 2 海洋表面的GPS散射信号DDM波形图 Fig. 2 GPS scattering delay Doppler map in ocean surface |
|
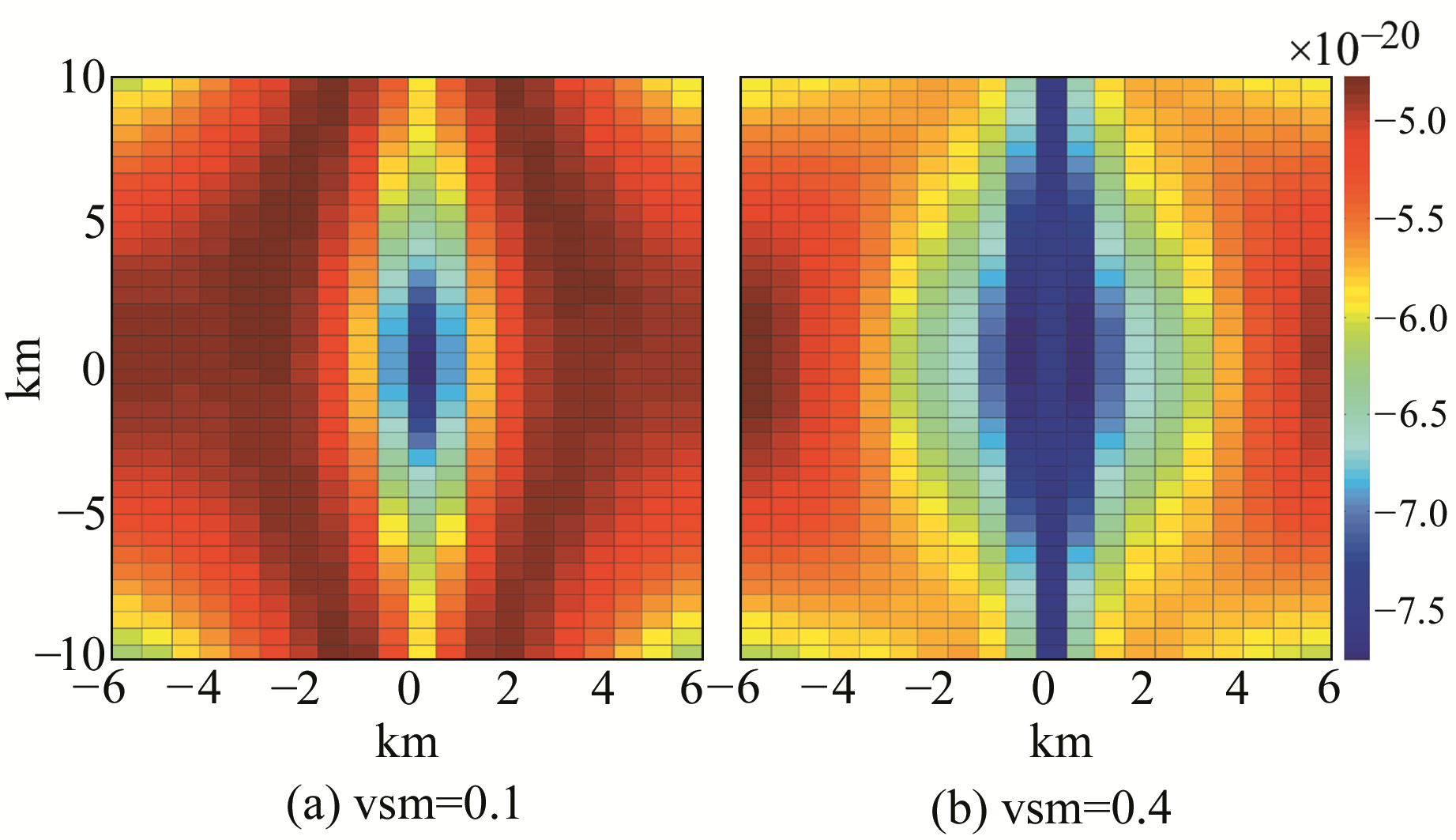
图 3 vsm=0.1和vsm=0.4时RR极化裸土GPS散射信号波形图 Fig. 3 GPS scattering map for RR pol(vsm=0.1, vsm=0.4) |
图 3模拟比较了RR极化时干燥土壤(vms=0.1)和潮湿土壤(vms=0.4)DDM波形图的差别。可以看出,土壤水分由干燥(vms=0.1)变化到较湿润(vms=0.4)时,DDM波形峰值范围变大,因此可以利用RR极化时DDM波形的变化对土壤水分的变化进行有效分析。
图 4给出了LR、VR和HR极化时,土壤水分由vsm=0.1变化到vsm=0.4时的GPS散射信号能量差。可以看出,在不同极化时,土壤水分变化对GPS散射信号的影响不同。

|
图 4 不同土壤水分含量(vsm=0.1和vsm=0.4)时LR、VR和HR极化的GPS散射信号能量差 Fig. 4 Power differences of different soil moisture for LR, VR and HR pol (vsm=0.1, vsm=0.4) |
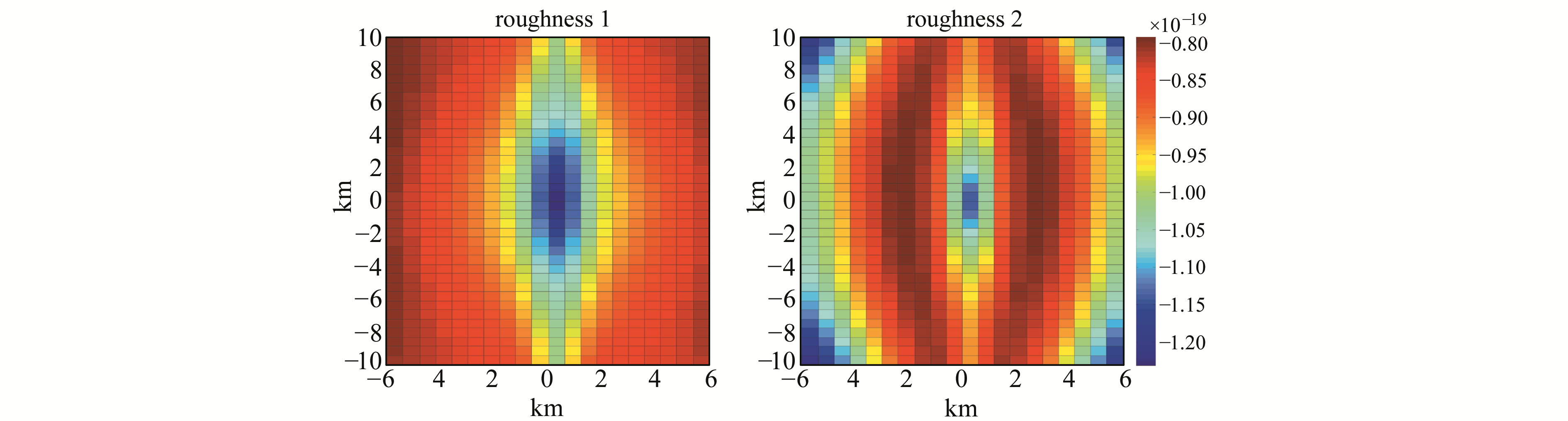
地表粗糙度是影响土壤水分反演的重要因素。在固定导航卫星频率、导航卫星/接收机位置和速度的情况下,保持土壤湿度(vsm=0.1)和土壤质地不变,考虑地表粗糙度变化(相关长度RMS和均方根高度cl)对GPS散射信号能量的影响。将2种不同的地表粗糙度分别记为roughness1(RMS=0.6 cm, cl=10 cm)、roughness2(RMS =0.1 cm, cl=20 cm),结果见图 5。
|
图 5 RR极化时不同粗糙度下的GPS散射信号波形图 Fig. 5 GPS scattering map for different surface roughness at RR pol |
从图 5可以看出,对于RR极化,地表粗糙度对GPS散射信号能量的影响较大。而在LR、VR和HR极化时,粗糙度变化导致的接收机能量差别较小(图 6)。
|
图 6 LR、VR和HR极化时地表粗糙度变化对GPS散射信号能量的影响 Fig. 6 Power differences for different surface roughness at LR, VR and HR pol |
本文建立了裸土的延迟多普勒图模型,该模型对载波频率的适用范围为1.0~89 GHz,可以模拟分析任意入射天顶角(0°~90°)、方位角(0°~360°)的延迟多普勒图波形信息,对地表参数中的粗糙度抽象为均方根高度和相关长度,具备模拟分析土壤水分对延迟多普勒图影响的功能。将本文针对陆面的模拟结果与文献[9]海洋延迟多普勒图结果进行比对,其模拟结果的数量级与文献[12]相同。针对具体参数的验证分析,将在后续研究中展开。
| [1] |
Rodriguez-Alvarez N, Camps A, Vall-Llossera M, et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique[J]. IEEE Transactions on Geoscience&Remote Sensing, 2011, 49(1): 71-84
(  0) 0) |
| [2] |
Larson K M, Small E E, Gutmann E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations:Initial Results[J]. GPS Solutions, 2008, 12(3): 173-177 DOI:10.1007/s10291-007-0076-6
(  0) 0) |
| [3] |
Small E E, Larson K M, Braun J J. Sensing Vegetation Growth with Reflected GPS Signals[J]. Geophysical Research Letters, 2010, 37(12): 245-269
(  0) 0) |
| [4] |
Chew C C, Small E E, Larson K M, et al. Effects of Near-Surface Soil Moisture on GPS SNR Data:Development of a Retrieval Algorithm for Soil Moisture[J]. IEEE Transactions on Geoscience&Remote Sensing, 2014, 52(1): 537-543
(  0) 0) |
| [5] |
Chew C C, Small E E, Larson K M, et al. Vegetation Sensing Using GPS-Interferometric Reflectometry:Theoretical Effects of Canopy Parameters on Signal-to-Noise Ratio Data[J]. IEEE Transactions on Geoscience&Remote Sensing, 2015, 53(5): 2755-2764
(  0) 0) |
| [6] |
王迎强, 严卫, 符养, 等. 机载GPS反射信号土壤湿度测量技术[J]. 遥感学报, 2009, 13(4): 670-685 (Wang Yingqiang, Yan Wei, Fu Yang, et al. Using Airborne GPS Reflected Signals for Soil Moisture Measurement[J]. Journal of Remote Sensing, 2009, 13(4): 670-685)
(  0) 0) |
| [7] |
Wan W, Larson K M, Small E E, et al. Using Geodetic GPS Receivers to Measure Vegetation Water Content[J]. GPS Solutions, 2014, 19(2): 237-248
(  0) 0) |
| [8] |
Chen K S, Wu T D, Tsang L, et al. Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three-Dimensional Moment Method Simulations[J]. IEEE Transactions on Geoscience&Remote Sensing, 2003, 41(1): 90-101
(  0) 0) |
| [9] |
Zavorotny V U, Voronovich A G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application[J]. IEEE Transactions on Geoscience&Remote Sensing, 2000, 38(2): 951-964
(  0) 0) |
| [10] |
Masters D S.Surface Remote Sensing Applications of GNSS Bistatic Radar: Soil Moisture and Aircraft Altimetry[D].Boulder: University of Colorado at Boulder, 2004
(  0) 0) |
| [11] |
Fung A, Eom H. Coherent Scattering of a Spherical Wave from an Irregular Surface[J]. IEEE Transactions on Antennas&Propagation, 1983, 31(1): 68-72
(  0) 0) |
| [12] |
Ulaby F T, Moore R K, Fung A K. Microwave Remote Sensing Active and Passive-Volume Ⅱ:Radar Remote Sensing and Surface Scattering and Enission Theory[M]. Boston: Addison-Wesley Publishing Company, 1982
(  0) 0) |
2. Key Laboratory of Planetary Sciences, CAS, 80 Nandan Road, Shanghai 200030, China;
3. School of Communication and Information Engineering, Shanghai University, 99 Shangda Road, Shanghai 200444, China;
4. Institute of Earthquake Science, CEA, 63 Fuxing Road, Beijing 100036, China
 2017, Vol. 37
2017, Vol. 37

