传感器在测量过程中会受到各种信号的干扰,导致其输出中随机噪声非常复杂。Allan方差法可以分离出随机干扰的组成部分,但是此方法只能分析静态条件下的随机误差。对于动态条件下的随机误差,有学者运用动态Allan方差进行分析[1-2],取得了很好的效果。但是由于动态Allan方差引入了窗函数的思想,使得参与计算的数据减少,导致功率泄露、方差估计值降低。使用Allan方差法时方差估计的置信度和信号动态变化跟踪效果相互矛盾,不可兼顾。
提高Allan方差估计置信度的方法有很多,包括总方差法[3]、重叠Allan方差法[4]等。其中,总方差法是通过倒镜像延拓将原始数据进行映射延拓,再用延拓后得到的数据计算Allan方差,从而提高估计值的置信度。基于这一思想,为了解决估计值置信度和信号动态跟踪效果的矛盾,本文构造了动态总方差法,首先将原始数据利用窗函数截取,然后将窗函数内数据用倒镜像映射的方法进行延拓来增加数据量,以提高估计的置信度,同时改善算法的动态跟踪效果。
1 总方差法原理及估计精度分析对Allan方差进行估计时,估计值的置信度取决于原始数据分组的独立组数。如果原始数据较少,则分成的组数和相互独立的组数必然较少,导致估计值的置信度低、估计误差大[5]。而总方差法利用倒镜像映射将原始数据进行延拓来增加数据量,进而增加独立组数,很好地解决了Allan方差法的不足。
记原序列为{xi},数据长度为N,映射后的序列为{xi*},数据延拓的映射规则为:
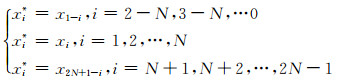
|
(1) |
通过映射将原始数据延长3倍,增加了独立组数,提高了估计置信度。序列{xi*}的标准差计算公式为:
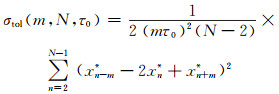
|
(2) |
式中,m为平均因子,且1≤m≤N-1,τ0为采样时间。记
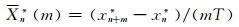
|
(3) |
式中,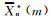
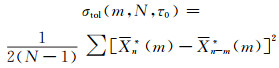
|
(4) |
通过以上推导可以看出,Allan方差估计的相关时间为Nτ0/2,是总方差法的1/2,因此总方差法的估计范围是Allan方差的2倍。
Allan方差估计值是一个随机变量,其估计误差为:
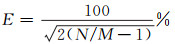
|
(5) |
式中,N为原始数据的数据长度,M为分组后各组的数据长度。
为了给出总方差法的估计误差,首先要给出等效自由度的概念。所谓等效自由度,就是当数据自由度不是整数时,由等效自由度来代替,它可以决定估计置信度的大小。等效自由度的计算公式为:
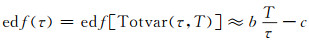
|
(6) |
式中,b、c的值取决于幂律谱噪声的类型,其具体值见表 1。
|
|
表 1 不同类型幂律谱噪声的b、c值 Tab. 1 b and c values of different types of power |
总方差法的估计误差为:
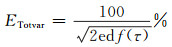
|
(7) |
通过式(3)~(5)可以看出,在N/M与T/τ相同的情况下,总方差法的估计误差要小于Allan方差法。
2 动态总方差法的构造总的来说,动态总方差法就是用窗函数截取原始数据,然后将截取得到的数据使用倒镜像映射的方法进行延拓,再计算延拓后数据的Allan方差和标准差,最后按时间顺序将Allan方差和标准差展现出来。动态总方差法的具体构造过程为:
1) 给定原始信号x(t)的时间起点t1。
2) 使用窗函数PW(t′)截取原始信号x(t),得到截取信号yT(t1),记窗函数的中心点为t1、宽度为L。截取信号yT(t1)为:
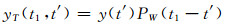
|
(8) |
3) 将信号yT(t1)进行倒镜像映射来进行拓展以增加数据量,映射规则在式(1)中已经给出。延拓后的序列记为y*T(t1, t′)。
4) 增量过程Δ(t1, t′, τ)为:
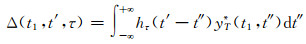
|
(9) |
其中,t′的变化范围为:
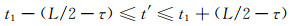
|
(10) |
式中,0≤τ≤τmax,τmax=L/3,则动态总方差的估计值为:
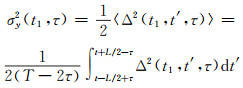
|
(11) |
式(11)也可以表达为:
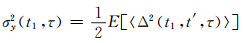
|
(12) |
5) 将窗口按确定的步长移动到下一个窗口t2,重复上述步骤,得到下一个方差估计值σy2(t2, τ)。依此类推,得到方差估计值序列{σy2(ti, τ)}, i=0, 1…N。为了观测噪声系数的随机变化规律,将方差估计值序列按时间顺序绘在σy-τ-t图中。
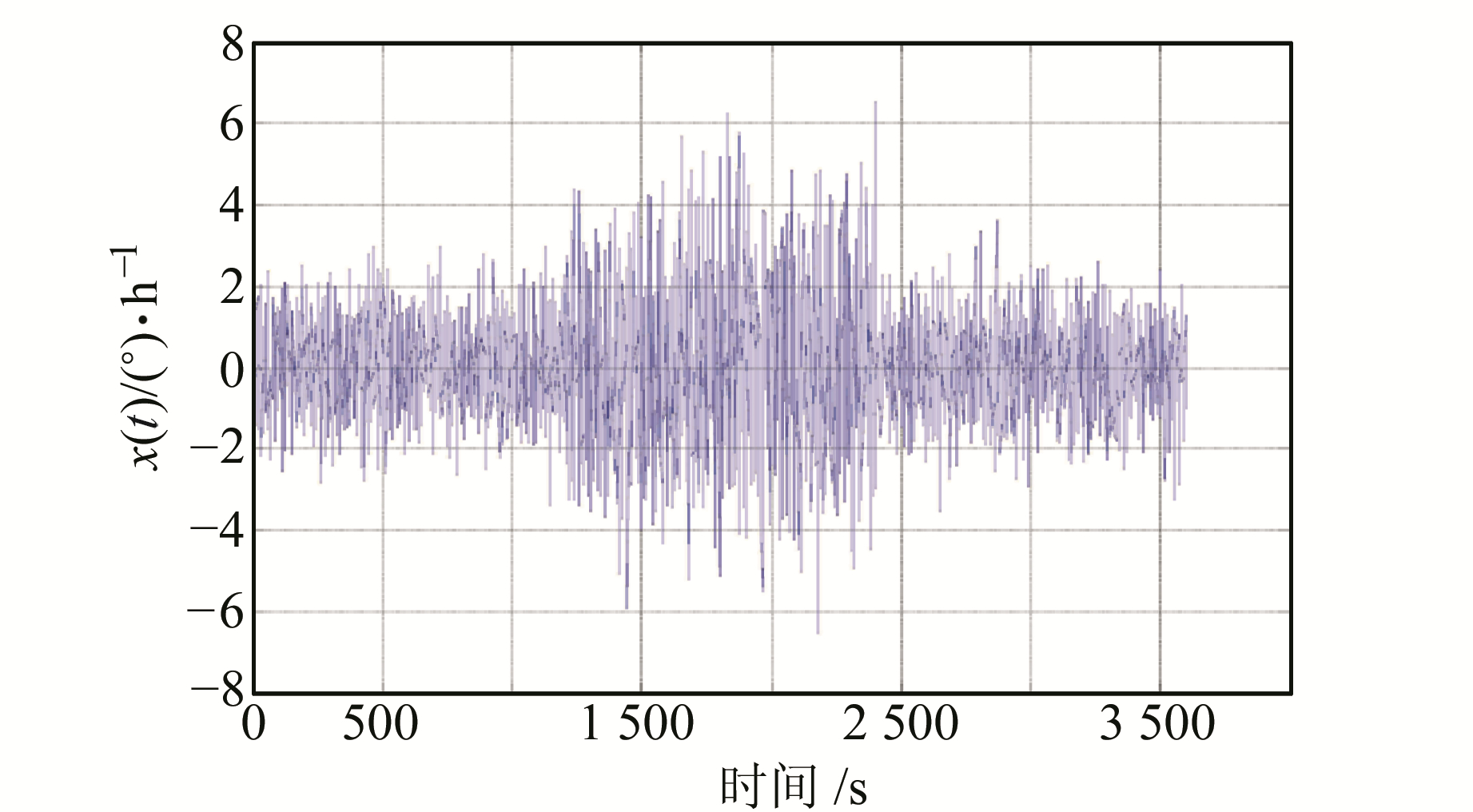
3 仿真实验当传感器在测量过程中受到干扰时,测得的信号在方差和幅值上就会有很大变化。假设传感器的输出信号如图 1所示,信号的平均值为0,初始段和末段的方差为1,中间的方差为2,每段均有1 200个数据。
|
图 1 非平稳随机噪声的仿真信号 Fig. 1 Simulation signal of non-stationary random noise |
分别用Allan方差法和总方差法对图 1仿真出的信号进行分析,结果见图 2。从图 2可以看出,当相关时间大于85 s以后,Allan方差法的分析结果开始出现较大偏差,而且越来越大,直至完全偏离;但是总方差法通过数据延拓增加了数据量和自由度,保持了很好的稳定性。

|
图 2 Allan方差法和总方差法分析结果 Fig. 2 Analysis results of Allan variance method and total variance method |
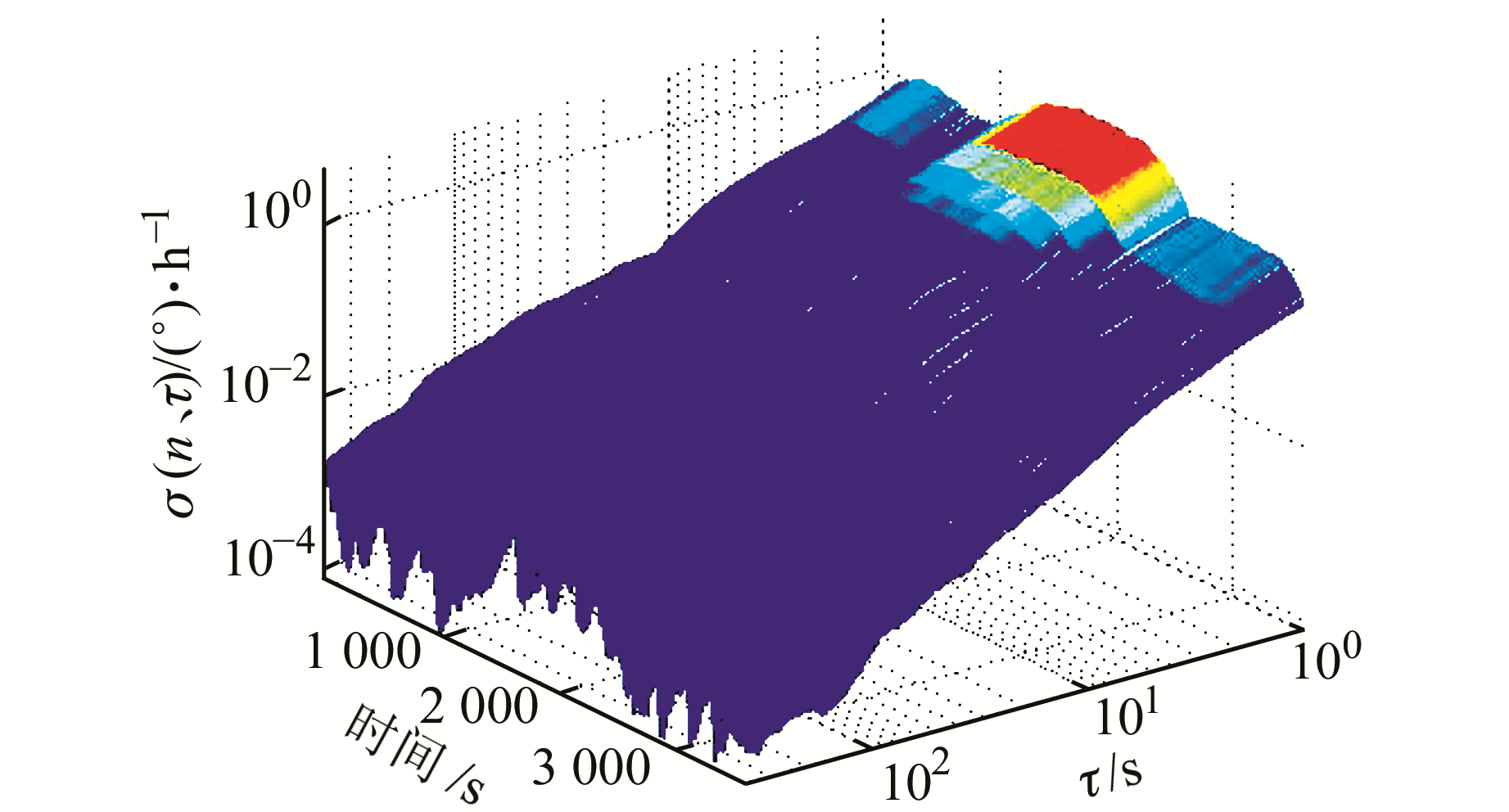
图 3为使用动态总方差法对仿真信号的分析结果。比较图 2和图 3可以看出,图 2仅可以表示出方差随采样时间的变化规律,而图 3同时表示出了方差随时间的变化规律。总之,动态总方差法的进步意义在于其可以及时跟踪原始信号在时间域的方差变化,并通过颜色的变化来显示方差的变化。
|
图 3 动态总方差法分析结果 Fig. 3 Analysis results of dynamic total variance method |
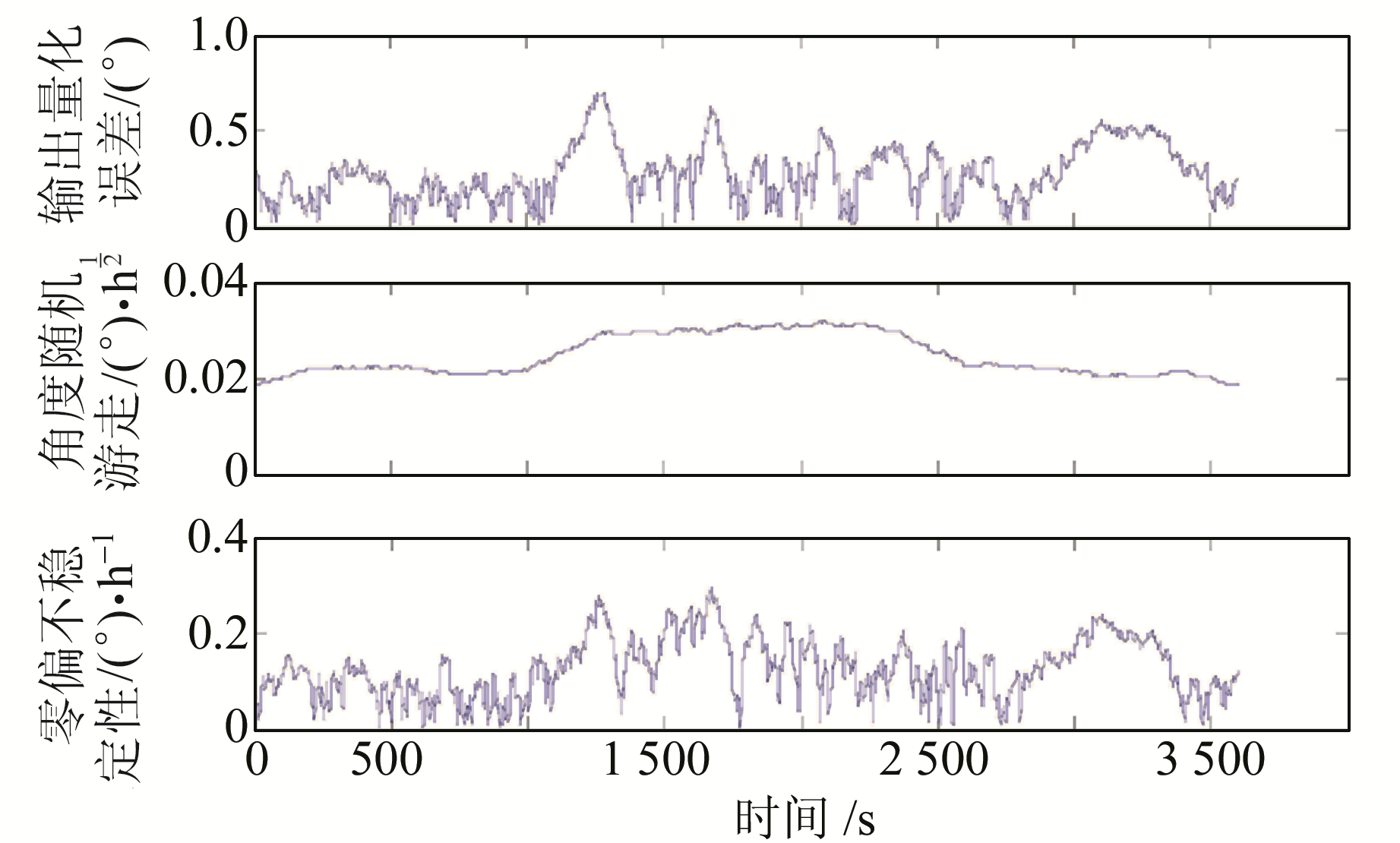
以陀螺的输出信号为例,将图 1所示的信号作为陀螺输出的随机噪声。陀螺的随机噪声分为角度随机游走、零偏不稳定性、速率随机游走、速率斜坡误差、马尔科夫噪声、输出量化误差等[6]。其中,角度随机游走是由激励信号不稳定或外界振动干扰引起的,零偏不稳定性是由速率的低频零偏波动引起的,输出量化误差是由模拟信号变为数字信号时的数字量化引起的[7]。这3个误差项的来源比较明确,所以选择其作为拟合对象。选取窗函数长度为401,分别使用动态Allan方差法和动态总方差法进行拟合,结果见图 4和图 5。

|
图 4 动态总方差法的分析结果 Fig. 4 Analysis results of dynamic total variance method |
|
图 5 动态Allan方差法的分析结果 Fig. 5 Analysis results of dynamic Allan variance method |
对比图 4和图 5可以看出,动态Allan方差对动态信号的分析效果明显不如动态总方差法,主要表现在:1)原始信号的方差突变发生在1 200 s和2 400 s,但是动态Allan方差法在跟踪时间上有明显的差异;2)在2 400 s后方差回归为1,随机误差减小,但是动态Allan方差的分析结果中量化噪声、零偏不稳定性依然保持了较大的值,与事实不相符。
4 结语Allan方差法在数据量少时,会出现估计值置信度低、估计误差大的情况。总方差法使用倒镜像映射的方法对数据进行延拓,增加了数据量和数据自由度,克服了置信度低、估计误差大的问题,但是总方差法无法及时跟踪数据的动态变化。为此,本文设计了动态总方差法,首先用窗函数截取原始数据,再对窗函数内的数据用倒镜像映射进行延拓,最后用仿真实验对比了动态总方差法与Allan方差法、总方差法、动态Allan方差法的分析结果。结果表明,动态总方差法不仅可以及时跟踪信号的动态变化,而且克服了长相关时间条件下估计置信度低、估计误差大的问题。
| [1] |
Dobrogowski A, Kasznia M.Real-time Assessment of Dynamic Allan Deviation and Dynamic Time Deviation[C].European Frequency and Time Forum, France, 2012
(  0) 0) |
| [2] |
高伟伟, 王广龙, 高凤岐, 等. 一种基于DAVAR的FOG随机信号处理新方法[J]. 解放军理工大学学报:自然科学版, 2014, 15(4): 330-334 (Gao Weiwei, Wang Guanglong, Gao Fengqi, et al. A New Method of Random Signal Processing Based on DAVAR[J]. Journal of PLA University of Science and Technology:Natural Science, 2014, 15(4): 330-334)
(  0) 0) |
| [3] |
Howe D A. The Total Deviation Approach to Long-Term Characterization of Frequency Stability[J]. IEEE Transactions on Ultrasonic, Ferroeletrics, and Frequency Control, 2000, 47(5): 1102-1110 DOI:10.1109/58.869040
(  0) 0) |
| [4] |
Riley W J.Techniques for Frequency Stability Analysis[C].IEEE International Frequency Control Symposium, Tampa, 2003
(  0) 0) |
| [5] |
程旭维, 汤霞清, 黄湘远. 基于#1理论方差的光学陀螺长期随机误差分析[J]. 中国激光, 2014(10): 146-153 (Cheng Xuwei, Tang Xiaqing, Huang Xiangyuan. Long Term Random Error Analysis of Optical Gyro Based on Variance of#1 Theory[J]. China Laser, 2014(10): 146-153)
(  0) 0) |
| [6] |
Institute of Electrical and Electronics Engineers.IEEE Standard Specification Format Guide and Test Procedure for Coriolis Vibratory Gyros[S].IEEE, 2001
(  0) 0) |
| [7] |
祁家毅, 任顺清, 冯士伟, 等. 半球谐振陀螺仪随机误差分析[J]. 中国惯性技术学报, 2009, 17(1): 98-101 (Qi Jiayi, Ren Shunqing, Feng Shiwei, et al. Analysis of Random Errors of Hemispherical Resonator Gyro[J]. Journal of Chinese Inertial Technology, 2009, 17(1): 98-101)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37


