2. 北斗导航应用技术河南省协同创新中心,郑州市科学大道62号,450001;
3. 中国建筑第七工程局交通建筑有限责任公司,郑州市城东路116号,450004
三维坐标转换中最重要是坐标转换参数的求解。坐标转换参数分为旋转、平移和尺度参数,其中旋转参数的确定是坐标转换的核心。传统的三维坐标转换模型用3个欧拉角构建旋转矩阵,所建立的模型是非线性的,需要用泰勒级数展开的方法将模型线性化,涉及到大量的三角函数计算,比较繁杂[1-5]。小角度旋转变换时,对旋转矩阵可用泰勒级数展开近似处理得到线性模型,如常用的布尔莎模型[6]。针对大旋角的旋转坐标转换,游为等[7]直接从三维直角坐标转换的非线性方程出发,采用基于同伦连续思想的Li-Yorke算法最优求解7个转换参数,该方法虽然适用于大旋角转换,但计算过程比较复杂。陈义等[8]提出一种旋转矩阵,利用9个方向余弦参数进行解算,该模型虽然适用于大旋角转换,但参与计算的模型参数达到13个。相对于传统的欧拉角和矩阵旋转表示方法,四元数拥有计算速度快、提供平滑插值以及存储空间较小等优势[9-12]。本文引入单位四元数来构造旋转矩阵,利用单位四元数理论推导一种直接求解空间坐标转换的算法,并通过仿真实验验证了该方法的有效性。
1 四元数及其性质 1.1 四元数的定义四元数是指由1个实数单位和3个虚数单位e1、e2、e3组成并具有下列形式实元的数[9-10]:

|
(1) |
式中,e1、e2、e3是直角坐标系中的3个基元。四元数的表示类似于字母
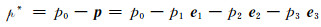
|
(2) |
四元数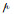


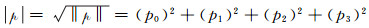
|
(3) |
当
四元数的加减法满足交换律和结合律:
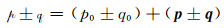
|
(4) |
2个四元数相乘又称为四元数的格拉斯曼积[2],四元数
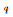
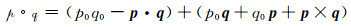
|
(5) |
式中,运算符号“°”表示四元数的格拉斯曼积。
四元数的格拉斯曼积满足分配律和结合律,但具有不可交换性,导致四元数的除法也具有不可交换性,除非除数是1个标量。四元数的除法定义为:
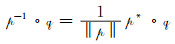
|
(6) |
式中,

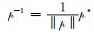
四元数还可以定义为[9]:

|
(7) |
对四元数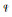

|
(8) |
式(8)可以认为是将四元数
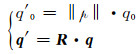
|
(9) |
式中,q′0是四元数

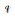
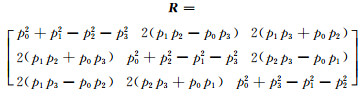
|
(10) |
式中,
设A点在空间直角坐标系o-uvw和o-xyz中的坐标分别为(u, v, w)和(x, y, z),a1、a2、a3为u轴与坐标系o-xyz中各轴间的方向余弦,b1、b2、b3为v轴与坐标系o-xyz中各轴间的方向余弦,c1、c2、c3为w轴与坐标系o-xyz中各轴间的方向余弦,缩放参数为λ,(Δx, Δy, Δz)为2个坐标系之间的平移参数,则有如下关系:
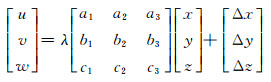
|
(11) |
式中,坐标系o-xyz分别绕z、y、x轴依次逆时针旋转γ、β、α角度,这时需要求取7个坐标转换参数λ、α、β、γ、Δx、Δy、Δz。
2.2 单位四元数与欧拉角的关系现有2个原点重合的坐标系Sa和Sb,若Sa分别绕z、y、x轴顺次逆时针旋转γ、β、α角度,则从Sa到Sb的旋转变换可得到由欧拉角计算单位四元数的公式:

|
(12) |
通过单位四元数计算欧拉角的公式为:
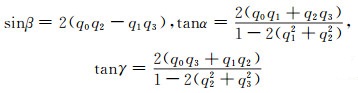
|
(13) |
设控制点坐标为[XTi, YTi, ZTi](i=1, 2,…, n),相应的模型坐标为[Xi, Yi, Zi] (i=1, 2,…, n)。根据n个控制点的两套坐标系坐标求解1个比例参数、3个平移参数和1个表示旋转的四元数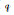
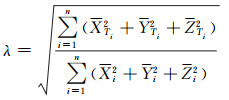
|
(14) |
单位四元数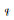

|
(15) |
将p展开,使

|
(16) |
结合式(5),式(16)可以写为:
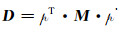
|
(17) |
式中,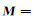
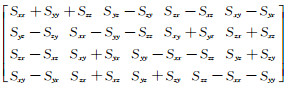


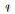
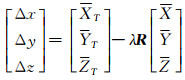
|
(18) |
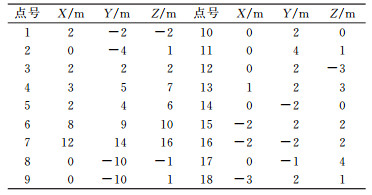
空间坐标转换的核心是确定坐标转换的旋转矩阵,尺度参数λ和3个平移参数[Δx Δy Δz]T的求取很容易。为了简明验证本文算法,令尺度参数λ=1,3个平移参数为0,源坐标系按Z轴、Y轴、X轴的顺序依次逆时针旋转,旋转角度依次为γ、β和α。模拟的源坐标系中控制点坐标见表 1。
|
|
表 1 源坐标系控制点坐标 Tab. 1 The control-points coordinate of source coordinates |
以Matlab软件为模拟平台,编程进行模拟实验。为不失一般性,随机生成旋转参数(欧拉角),即α=360°·(R-0.5), β=360°·(R-0.5), γ=360°·(R-0.5),R∈[0, 1]。设仿真步长为1 s,仿真周期为500 s。为了获取目标坐标系中控制点坐标数据,按照上述随机取样的旋转参数和空间坐标转换公式(11),对表 1源坐标系中控制点坐标进行空间坐标转换,可计算出500组转换后的坐标。为了验证该算法的坐标转换精度,在上述500组坐标结果中加入高斯白噪声(μ=0, σ=1),得到最终的500组目标坐标系下的控制点坐标。
3.1 单位四元数解算结果及分析利用3个欧拉角,通过式(12)计算相应的单位四元数值;利用源坐标系和目标坐标系的两套控制点坐标,通过式(17)求取矩阵M的最大特征值对应的特征向量,反算文中所提算法的单位四元数值。直接计算和文中所提算法反算的单位四元数残差分析结果(单位四元数无量纲,文中暂不考虑其单位)见图 1和表 2。

|
图 1 相对应的单位四元数残差 Fig. 1 The corresponding unit quaternion residuals |
|
|
表 2 单位四元数残差分析结果 Tab. 2 Unit quaternion residual analysis results |
从表 2看出,通过两套坐标系随机取样500组坐标反算的单位四元数结果与直接计算的单位四元数结果的残差很小,均值几乎为0,而且适用于任意角度的旋转变换。从图 1看出,反算的单位四元数与直接计算的单位四元数的残差在(-0.04, 0.04)之间跳变,而且所得残差的均值相当于实验设计时所加入的高斯白噪声的水平。
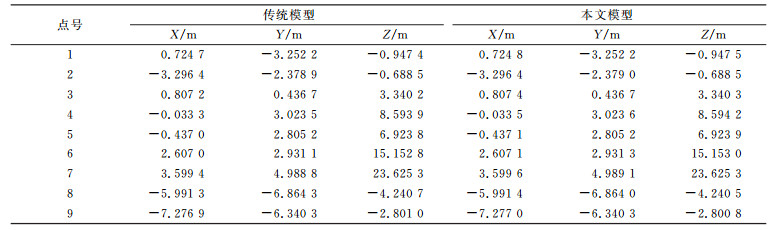
3.2 坐标解算结果及分析利用传统的欧拉角坐标转换方法,参照式(10)构造旋转矩阵,选取表 1中源坐标系下前9个控制点的坐标,按照α=20°、β=40°、γ=60°进行坐标转换,得到目标坐标系下的控制点坐标,转换结果见表 3。同理,将表 1中后9个源坐标系控制点坐标,按照α=30°、β=50°、γ=70°进行坐标转换,结果见表 4。
|
|
表 3 前9个控制点坐标转换结果 Tab. 3 First nine control points coordinate transformation results |
|
|
表 4 后9个控制点坐标转换结果 Tab. 4 Last nine control points coordinate transformation results |
从表 3和表 4看出,利用单位四元数构造旋转矩阵进行坐标转换的转换结果和传统的欧拉角构造旋转矩阵的坐标转换结果相差很小,证明了利用单位四元数进行坐标转换的有效性。从图 1可以得出,大量的实验验证了通过源坐标系坐标和目标坐标系坐标反算的单位四元数和直接计算的单位四元数相差很小,证明了本文算法的正确性。仿真实验验证了本文算法可用于任意角度旋转的坐标转换。
4 结语本文从四元数的性质以及运算入手,针对三维空间坐标转换模型的参数求解问题,引入四元数来构造旋转矩阵,在理论上证明了坐标转换旋转矩阵等价于四元数的正交变换。利用单位四元数旋转变换表示方向余弦矩阵,推导了基于单位四元数的三维坐标转换模型。与常规的坐标转换模型相比。该模型用代数运算替代了繁琐的三角运算,无需对旋转参数进行线性化,模型简单,计算简便,可用于任意旋转角度的坐标转换,且能够保证转换精度。
| [1] |
田桂娥, 宋利杰, 尹利文. 地方坐标系与CGCS2000坐标系转换方法的研究[J]. 测绘工程, 2014, 23(8): 66-69 (Tian Guie, Song Lijie, Yin Liwen. The Method of Coordinate Transformation between Local Coordinate and CGCS2000[J]. Engineering of Surveying and Mapping, 2014, 23(8): 66-69 DOI:10.3969/j.issn.1006-7949.2014.08.016)
(  0) 0) |
| [2] |
段鹏硕, 刘根友, 龚有亮, 等. 空间坐标系变换的函数梯度描述方法[J]. 测绘学报, 2014, 43(10): 1005-1012 (Duan Pengshuo, Liu Genyou, Gong Youliang, et al. The Functional Gradient Description Method of Space Coordinate Transformation[J]. Acta Geodactica et Cartographica Sinica, 2014, 43(10): 1005-1012)
(  0) 0) |
| [3] |
刘毅, 岳建平, 卢银宏, 等. 补偿最小二乘法在大地坐标转换中的应用[J]. 测绘工程, 2012, 21(5): 80-82 (Liu Yi, Yue Jianping, Lu Yinhong, et al. Application of Penalized Least Squares Method in Geodetic Coordinate System Transformation[J]. Engineering of Surveying and Mapping, 2012, 21(5): 80-82 DOI:10.3969/j.issn.1006-7949.2012.05.021)
(  0) 0) |
| [4] |
潘国荣, 周跃寅. 两种坐标系转换计算方法的比较[J]. 大地测量与地球动力学, 2011, 31(3): 58-62 (Pan Guorong, Zhou Yueyin. Comparison between Two Ways of Calculation of Coordinate Transfer[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 58-62)
(  0) 0) |
| [5] |
田茂, 花向红, 丁鸽, 等. 基于罗德里格矩阵的混合最小二乘方法在三维激光中的应用[J]. 测绘地理信息, 2014, 39(2): 18-21 (Tian Mao, Hua Xianghong, Ding Ge, et al. Three-Dimensional Laser Scanning Technology Research Application Based on Mixed Least Squares in Rodrigue Matrix[J]. Journal of Geomatics, 2014, 39(2): 18-21)
(  0) 0) |
| [6] |
倪飞, 房世龙, 赵苏政. 拟准检定法在坐标系统转换中的应用研究[J]. 测绘地理信息, 2015, 40(6): 15-18 (Ni Fei, Fang Shilong, Zhao Suzheng. Application of QUAD Method in Coordinate Transformation[J]. Journal of Geomatics, 2015, 40(6): 15-18)
(  0) 0) |
| [7] |
游为, 范东明, 黄瑞金. 适用于任意旋转角的三维直角坐标转换方法[J]. 测绘科学, 2009, 34(5): 154-155 (You Wei, Fan Dongming, Huang Ruijin. A Method of 3D Rectangular Coordinate Transformation Adapted to Any Rotation Angle[J]. Science of Surveying and Mapping, 2009, 34(5): 154-155)
(  0) 0) |
| [8] |
陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1101-1105 (Chen Yi, Shen Yunzhong, Liu Dajie. A Simplified Model of Three Dimensional-Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1101-1105)
(  0) 0) |
| [9] |
Pujol J. On Hamilton's Nearly-Forgotten Early Work on the Relation between Rotations and Quaternions and on the Composition of Rotation[J]. American Mathematical Monthly, 2014, 121(6): 515-522 DOI:10.4169/amer.math.monthly.121.06.515
(  0) 0) |
| [10] |
Tsougenis E D, Papakostas G A, Koulouriotis D E, et al. Adaptive Color Image Watermarking by the Use of Quaternion Image Moments[J]. Expert Systems with Applications, 2014, 41(14): 6408-6418 DOI:10.1016/j.eswa.2014.04.021
(  0) 0) |
| [11] |
杜兰, 张捍卫, 周庆勇, 等. 坐标转换参数之间的相关性解析[J]. 大地测量与地球动力学, 2011, 31(1): 59-62 (Du Lan, Zhang Hanwei, Zhou Qingyong, et al. Analysis of Correlation of Coordinate Transformation Parameters[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 59-62)
(  0) 0) |
| [12] |
徐芳, 梅文胜. 旋转矩阵表达方法对相机检校的影响[J]. 测绘地理信息, 2014, 39(2): 13-17 (Xu Fang, Mei Wensheng. Camera Calibration Effects of Rotation Matrix Expression[J]. Journal of Geomatics, 2014, 39(2): 13-17)
(  0) 0) |
2. Beidou Navigation Technology Collaborative Innovation Center of Henan, 62 Kexue Road, Zhengzhou 450001, China;
3. China Construction Seventh Bureau Traffic Construction Co Ltd, 116 Chengdong Road, Zhengzhou 450004, China
 2017, Vol. 37
2017, Vol. 37