2. 北斗导航应用技术河南省协同创新中心,郑州市科学大道62号,450001;
3. 成都信息工程大学大气探测重点实验室,成都市学府路一段24号,610225
全球弧段的卫星精密定轨需选用全球网跟踪站进行参数估计,其解算效率与跟踪站数量及观测量组合方式相关。但其解算精度并不与跟踪站数量正相关,当跟踪站达到一定数量时,定轨精度的提升将趋于缓和,可定义达到一定精度下的跟踪站数为该定轨精度下的测站饱和点。一般选用分布较为均匀的跟踪站进行卫星精密定轨,而选用多少数量的跟踪站却并无详细的规定[1]。假设每个跟踪站平均能观测到10~14颗卫星,根据Walker-δ星座的对称特点[2],完成全部卫星(32颗GPS卫星)的全弧段观测仅需不到10个跟踪站。但仅有10个跟踪站的观测数据无法满足cm级高精度定轨的需求。卫星精密定轨是多观测信息下的参数估计过程,随着待估参数的增加,往往需要更多的跟踪站参与全弧段估计。由参数估计的特点可知,多余观测量对参数的数值解是有利的,但并不能有效提升待估参数的精度,因此,选择跟踪站的数量对卫星精密定轨有重要意义。最简单的方法是依据排列组合进行定轨比较,但对全球500多个跟踪站进行组合并精密定轨,耗时太长且计算量庞大,不适用于近实时的超快速轨道解算。
全球均匀选站比较简单的方法是对全球跟踪站进行格网划分,对不同格网选一定数量的跟踪站。格网法实现简单但需要频繁变换格网划分的尺度,容易损失核心站。本文提出一种基于不规则三角网(TIN)的选站方法,能快速稳定地完成给定基数的跟踪站选择。
1 全球跟踪站均匀选择原理全球IGS站主要分布在南北纬80°内,可以完成各大导航系统轨道的全弧段观测。但如果所有IGS站参与精密定轨数据处理,系数矩阵会过于庞大,处理效率缓慢。目前已有学者通过50个均匀分布的IGS站完成了优于3 cm的精密定轨[3],相比100个IGS站,解算效率提升3倍。可见,全球均匀选站使卫星精密定轨的实效性得到极大提升。随机对500个站进行组合比较困难,本文通过格网和不规则三角网的方式对跟踪站进行均匀选择。
1.1 跟踪站格网分布模型格网划分的目的是将众多离散点进行分区。要实现全球均匀选站,只需要从每块分区中选一定数量站,其关键在于格网步长的划分,显然变步长划分方式可以较灵活地实现随机站数的选择。为方便格网设计,只需要采用跟踪站的经纬度进行二维平面格网划分。定义经度范围0°~360°,纬度范围-80°~80°。IGS站呈现全球分布、分块相对集中的特点,选站采用平均划分、相对集中的方法。格网以10n×10n(n=1, 2, 3, 4…)进行划分,格网数为:

|
(1) |
[]表示向上取整,对应的格网数见表 1。
|
|
表 1 格网分区数目表 Tab. 1 Number of grid |
由表 1可知,n=2, 3, 4均可以满足150个以内格网选站。以20°×20°为例,全球格网分布如图 1所示。
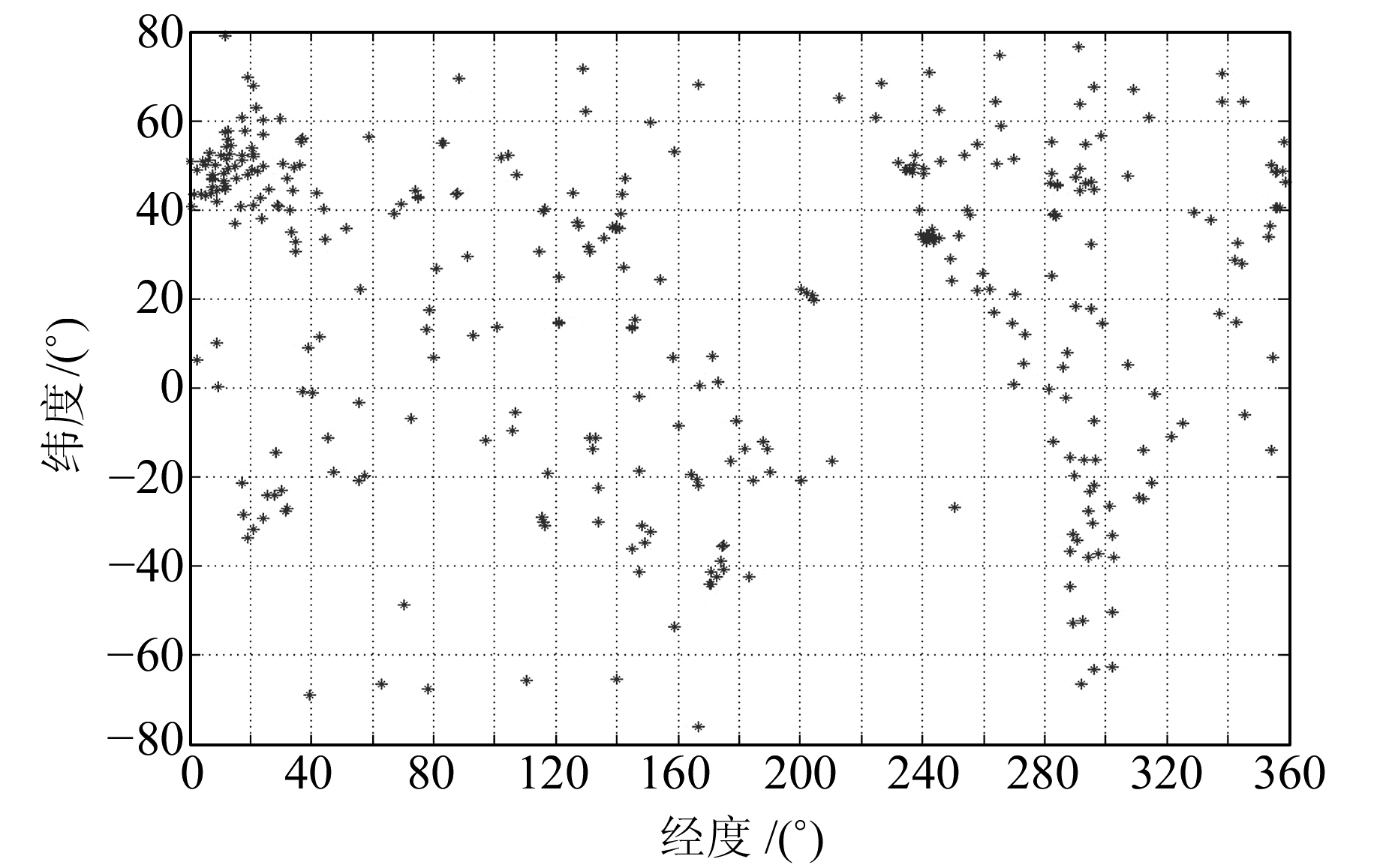
|
图 1 20°×20°格网跟踪站分布示意图 Fig. 1 Distribution of 20°×20°grid stations |
由于海洋面积占地表总面积71%左右,而跟踪站在美洲大陆及欧亚大陆相对集中,因此格网选站无法满足每个格网均能覆盖跟踪站。考虑此因素,本文不采用格网的方式进行全球选站研究。
1.2 跟踪站不规则三角网分布模型格网模型分块均匀,原理简单,但不能细化相对集中分布的跟踪站,因此需要在格网内再次进行优选,降低选站判决复杂度并减小选站计算量。
在数字DEM模型中,基于不规则三角网的数学模型有优良的重构特性,既减少了规则格网带来的数据冗余,同时在计算(如坡度)效率方面又优于单一的基于等高线的方法[4]。基于三角形的表面建模适合于所有的数据结构,且三角形在形状和大小方面有很大的灵活性。
本文以TIN网构造方法,将所有IGS站按Delaunay法则三角化,并以拓扑关系的公共点重复率为几何选站依据,快速完成任意站数的选择。以Delaunay法则建立全球站的三角网拓扑关系,每个跟踪站均是三角网的拓扑基元,无需重构跟踪站分布模型,完成选站的同时能够保证跟踪站的全球相对均匀分布。全球IGS站TIN网型图如图 2所示。

|
图 2 全球IGS站TIN网型图 Fig. 2 TIN network of global IGS stations |
跟踪站TIN网分布模型是重构全球网的过程,而依据何种法则是构造TIN的关键。本文主要研究以Delaunay法则建立TIN网,自主设计一套跟踪站全球TIN网构建软件,配合PANDA定轨软件[5]完成数据测试。
1.3.1 基于Delaunay法则不规则三角网的生成Delaunay三角网法则是构造不规则三角网的重要方法之一[6-8]。由Delaunay构成的三角网满足以下条件:每个三角形由3个相邻的点连接而成;三角形的外接圆内不包含其他点;三角形相互邻接互不重叠。
基于Delaunay法则,采用三角网生长算法进一步得到不规则三角网。其步骤如下[9-10]:
1) 选取任一跟踪站,查找距该跟踪站最近的跟踪站并连接之,作为初始基线;
2) 在初始基线右侧运用Delaunay法则搜寻第3点,即距初始基线最近的点;
3) 生成Delaunay三角形,以三角形2条新边作为新基线;
4) 重复步骤2、3,直至所有基线处理完毕。
三角网生长算法快速简单,所生成的三角网规则性较好,易得到全球跟踪站的拓扑关系。图 3给出了三角网生长示意图。

|
图 3 三角网生长示意图 Fig. 3 Sketch of triangulation growth |
点、线和连接关系是TIN三角网拓扑观测三大要素。显然,研究公用点是本文选站的重要手段。TIN网中各点在各三角形中使用的次数称为重复率。重复率高的跟踪站被优先选择,如出现重复率相同的跟踪站,按跟踪站观测数据质量择优选取(进行简单的数据预处理,如计算周跳比、信噪比、粗差及多路径影响等)。基于TIN网的选站模型,避免了全球分区模糊和各区跟踪站不均匀问题。通过拓扑关系选择核心点,容易得到全球网型。图 4给出TIN网选站后30~150个跟踪站的分布(考虑篇幅,本文仅给出30、50、70、120个跟踪站分布)。

|
图 4 不同跟踪站数分布 Fig. 4 Distribution map of different numbers of stations |
所选跟踪站相当于全网的特征点,对这些跟踪站采用TIN法重构三角网,恢复跟踪站全网布局,比较所选跟踪站与全网的相似度。图 5为选定跟踪站的TIN网拓扑图。

|
图 5 不同跟踪站TIN网重构图 Fig. 5 TIN reconstruction of different numbers of stations |
由图 5可得,基于拓扑关系的TIN网选站模型并未破坏跟踪站的全球分布特性,且随站数增加,网型逐步逼近全网模型。同时,基于TIN网的选站方法优先全网逼近,然后局部细化,即在优先满足全球分布的条件下,可进一步将剩余站细化到跟踪站较多的地区。
1.3.3 选站实时应用本文基于TIN网跟踪站选站模型,开发了一套符合PANDA定轨要求的软件,可进行任意跟踪站数的精密定轨,对进一步研究精密定轨测站饱和点有重要的数据佐证意义。
首先对下载的跟踪站(非基准站,即始终需要固定的跟踪站)进行位置确定,可通过IGS公布的SNX文件查找先验值或伪距单点定位确定,然后对所有跟踪站进行TIN网拓扑关系构造,统计各跟踪站在三角网中的重复率。按重复率优先原则选站,重复率相等的跟踪站按数据质量(数据预处理结果)选取,并将选择的跟踪站参与精密定轨处理,其流程如图 6所示。

|
图 6 基于TIN网选站定轨流程图 Fig. 6 TIN-based station-selecting flowchart for orbit determination |
本文选择2015年年积日313~320进行8 d精密定轨测试,每天均按20~150个跟踪站(以10递增)参与解算,并统计定轨处理时间及轨道精度。测试平台为OpenSUSE_x64系统,CPU主频2.0 GHz共32线程,内存32 GB。由于参与全球选站的部分跟踪站接收机类型不在IGS08.ATX文件中,精密定轨数据预处理前会将该类跟踪站剔除,故实际参与解算的全球跟踪站可能会少于标定的选定站数。经处理发现,因跟踪站接收机类型不被识别而剔除的少于5个,且在20~50站数时被剔除少于2个,在60~100站数时被剔除少于3个,在110以上站数时被剔除4~5个。故在结果统计中不考虑剔除站数对结果的影响,统一按初始标定站数统计。
表 2给出8 d不同跟踪站下精密定轨(单天解)的处理时间及精度(与IGS最终轨道互差径向RMS)结果均值。
|
|
表 2 定轨精度、耗时8 d均值 Tab. 2 Mean value of 8 days orbit precision-processing time |
由表 2可以看出,随着站数的增加,精密定轨处理时间明显增加,而定轨精度在90站后无明显提升。8 d定轨结果如图 7所示。

|
图 7 轨道精度-时间趋势 Fig. 7 Orbit precision-time trend |
由图 7可知,30个跟踪站即可完成GPS优于50 mm精度的精密定轨;当跟踪站个数达到70时,GPS定轨精度增长缓和;达到90后,定轨精度已无明显提高。综合各天统计结果,初步得到GPS定轨精度的测站饱和点在90左右。显然,定轨处理时间与跟踪站数量增加不成正比。原因在于,待估参数的增加扩大了系数阵的维数,矩阵运算占用大量资源,计算效率明显下降。同时,这为分网估计提供了很好的选站参考,多重全网估计更能提升解算效率和精度。
3 结语在精密定轨数据处理中,数据质量与观测网构型都直接影响轨道精度。全网估计可以得到更高的轨道精度,但牺牲了内存资源和处理时间。因而,选择适当的跟踪站数量对快速高精度定轨及分网定轨有重要意义。本文通过TIN网拓扑结构快速完成跟踪站全球网选择,结果表明,70个跟踪站就可完成精度优于30 mm的精密定轨,处理时间相比140个跟踪站缩短三分之二。而达到90个跟踪站后,精度提升幅度限制在1 mm内。该选站方法可推广运用于实时精密定轨及实时钟差的跟踪站选择,同时可为多重全网估计提供一种可行的子网跟踪站选择方案。通过长期定轨测试,可进一步研究全球跟踪站利用率,对我国北斗卫星导航系统全球监测网建设有一定指导意义。
致谢: 感谢信息工程大学iGMAS分析中心提供的数据!
| [1] |
杨晓龙, 刘忠汉. 基于覆盖性能的Walker-δ星座构型保持[J]. 空间控制技术与应用, 2012, 38(2): 53-57 (Yang Xiaolong, Liu Zhonghan. Walker-δ Constellation Configuration Maintenance Based on Coverage Performance[J]. Aerospace Control and Application, 2012, 38(2): 53-57 DOI:10.3969/j.issn.1674-1579.2012.02.011)
(  0) 0) |
| [2] |
施闯, 赵齐乐, 楼益栋, 等. 卫星导航系统综合分析处理软件PANDA及研究进展[J]. 航天器工程, 2009, 18(4): 64-70 (Shi Chuang, Zhao Qile, Lou Yidong, et al. PANDA:Comprehensive Processing Software for Satellite Navigation Systems and Its Research Progress[J]. Spacecraft Engineering, 2009, 18(4): 64-70 DOI:10.3969/j.issn.1673-8748.2009.04.012)
(  0) 0) |
| [3] |
朱杰, 夏青. 一种基于TIN三角网数据的规则格网生成算法[J]. 海洋测绘, 2009, 29(3): 38-40 (Zhu Jie, Xia Qing. Algorithm for Building Grid DEM Based on TIN DEM Data[J]. Hydrographic Surveying and Charting, 2009, 29(3): 38-40 DOI:10.3969/j.issn.1671-3044.2009.03.012)
(  0) 0) |
| [4] |
廖国忠, 张伟, 梁生贤. 基于规则三角网的等值线追踪与填充算法的实现和应用[J]. 物探化探计算技术, 2014, 36(1): 120-123 (Liao Guozhong, Zhang Wei, Liang Shengxian, et al. Realization and Application of Algorithm Based on Rule Triangulated Network of the Contour Tracing and Filling[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014, 36(1): 120-123 DOI:10.3969/j.issn.1001-1749.2014.01.19)
(  0) 0) |
| [5] |
赵齐乐, 刘经南, 葛茂荣, 等. 用PANDA对GPS和CHAMP卫星精密定轨[J]. 大地测量与地球动力学, 2005, 25(2): 113-117 (Zhao Qile, Liu Jingnan, Ge Maorong, et al. Precise Orbit Determination of GPS and CHAMP Satellites with PANDA Software[J]. Journal of Geodesy and Geodynamics, 2005, 25(2): 113-117)
(  0) 0) |
| [6] |
江剑霞, 刘少华, 严汉英. VB环境下不规则三角网的算法设计与实现[J]. 四川测绘, 2006, 29(2): 64-67 (Jiang Jianxia, Liu Shaohua, Yan Hanying. Algorithm Designing and Realizing of TIN in VB[J]. Surveying and Mapping of Sichuan, 2006, 29(2): 64-67 DOI:10.3969/j.issn.1674-5019.2006.02.004)
(  0) 0) |
| [7] |
余代俊, 蒲朝旭, 朱逍贤. 一种Delaunay三角剖分的改进算法[J]. 测绘通报, 2014(6): 51-54 (Yu Daijun, Pu Zhaoxu, Zhu Xiaoxian. An Improvement Algorithm for Delaunay Triangulation[J]. Bulletin of Surveying and Mapping, 2014(6): 51-54)
(  0) 0) |
| [8] |
刘伟平, 郝金明, 于合理, 等. 导航卫星精密轨道与钟差确定方法研究及精度分析[J]. 测绘通报, 2014(5): 5-7 (Liu Weiping, Hao Jinming, Yu Heli, et al. Study on the Method of Precise Navigation Satellite Orbit and Clock Determination and Accuracy Analysis[J]. Bulletin of Surveying and Mapping, 2014(5): 5-7)
(  0) 0) |
| [9] |
韩元利. 网格总分并行式Delaunay三角网建模方法[J]. 测绘学报, 2015, 44(6): 702-708 (Han Yuanli. A General-Division Grid Pattern Delaunay-TIN Parallel Algorithm[J]. Acta Geodaetica et Cartographics Sinica, 2015, 44(6): 702-708)
(  0) 0) |
| [10] |
崔雪森, 杨胜龙, 樊伟. 基于栅格局部细分的带约束的不规则三角网生成算法[J]. 测绘学报, 2008, 37(2): 196-199 (Cui Xuesen, Yang Shenglong, Fan Wei. Grid Based Local Subdivision Algorithms for Constructing Triangulated Irregular Network under Restriction Conditions[J]. Acta Geodaetica et Cartographics Sinica, 2008, 37(2): 196-199 DOI:10.3321/j.issn:1001-1595.2008.02.012)
(  0) 0) |
2. Beidou Navigation Technology Collaborative Innovation Center of Henan, 62 Kexue Road, Zhengzhou 450001, China;
3. Key Laboratory of Atmospheric Detection, Chengdu University of Information Technology, 24 First-Xuefu Road, Chengdu 610225, China
 2017, Vol. 37
2017, Vol. 37



