2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006;
3. 钦州学院资源与环境学院,钦州市滨海大道12号,535000
国内外学者通常采用两种方式对TEC值进行预报:一种是利用现有电离层经典模型,如Klobuchar模型[1]、IRI模型[2]等,一些学者对经典模型进行改进从而建立了区域性实用模型,并取得较好的成果[3-5];另一种是利用区域TEC观测数据,采用不同模型进行短期预报,如时间序列模型[6-8]、神经网络模型[9-10]、频谱分析[11]、最小二乘配置[12]等。尽管以上方法对TEC值预报取得了良好效果,但仍存在模型参数选取困难、网络优化难、研究范围单一等不足。
Holt-Winters模型是对具有季节变动、线性趋势和随机波动的时间序列进行分解,并与指数平滑法结合,对所得分解量作出估计,建立预测模型并外推预测值,在不同领域取得了较好的应用效果[13-15],为电离层TEC预报提供了新方法。针对电离层TEC的季节性变化特性,本文采用Holt-Winters加法模型和乘法模型对IGS中心提供的电离层TEC数据进行预报,并将预报值与IGS中心的电离层TEC值进行对比,评估其预报精度。
1 Holt-Winters模型简介Holt-Winters模型[16-17]是一种基于统计学的时序数据的预报模型,能对任何没有明显函数规律、但确实存在某种关联并带有趋势项和季节变化项的时间序列进行短期预报,对重复性和季节性趋势数据具有较好的预报能力。其包括无季节模型、加法模型和乘法模型3种。
1) 无季节模型。适用于无季节性变化的序列,其基本公式为:
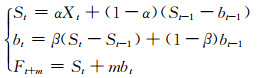
|
(1) |
2) 加法模型。适用于具有加法季节变化的序列,其基本公式为:
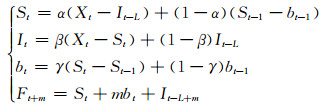
|
(2) |
3) 乘法模型。适用于具有乘法季节变化的序列,基本公式为:
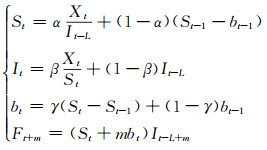
|
(3) |
式(1)~(3)中,Xt为时刻t的观测值;St为时刻t的稳定成分;It为时刻t的季节成分;bt为时刻t的趋势成分;m为预测期数,m>0;Ft+m为m期的预测值;L为季节长度;α、β、γ为平滑参数,α、β、γ∈ [0, 1]。
2 实验分析 2.1 数据选取根据太阳黑子数的11 a周期变化情况,选取IGS中心提供的2010年年积日101~114、2011年年积日232~245、2012年年积日18~31和2014年年积日143~156高纬度(72.5°N, 130°E)、中纬度(37.5°N, 130°E)和低纬度(5°N, 130°E)数据作为电离层平静期样本序列;选取2013年年积日152~165和231~244高纬度(72.5°N, 130°E)、中纬度(37.5°N, 130°E)和低纬度(5°N, 130°E)数据作为电离层活跃期样本序列。利用所选数据前8 d的TEC值作为样本序列,采用加法模型和乘法模型预测后6 d的TEC值。将IGS中心提供的观测数据作为真值,将预报结果与其比较,采用日平均相对精度P和均方根误差RMSE评定预报精度。其相应的定义如下:
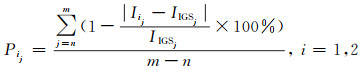
|
(4) |
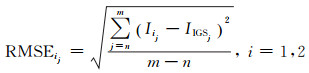
|
(5) |
式中,i=1为加法模型,i=2为乘法模型;Iij为第j个历元的预报值;IIGSj为第j个历元IGS中心的观测值;|Iij-IIGSj |为第j个历元预报值与真值之差的绝对值;n为时段的起始历元;m为时段的结束历元。
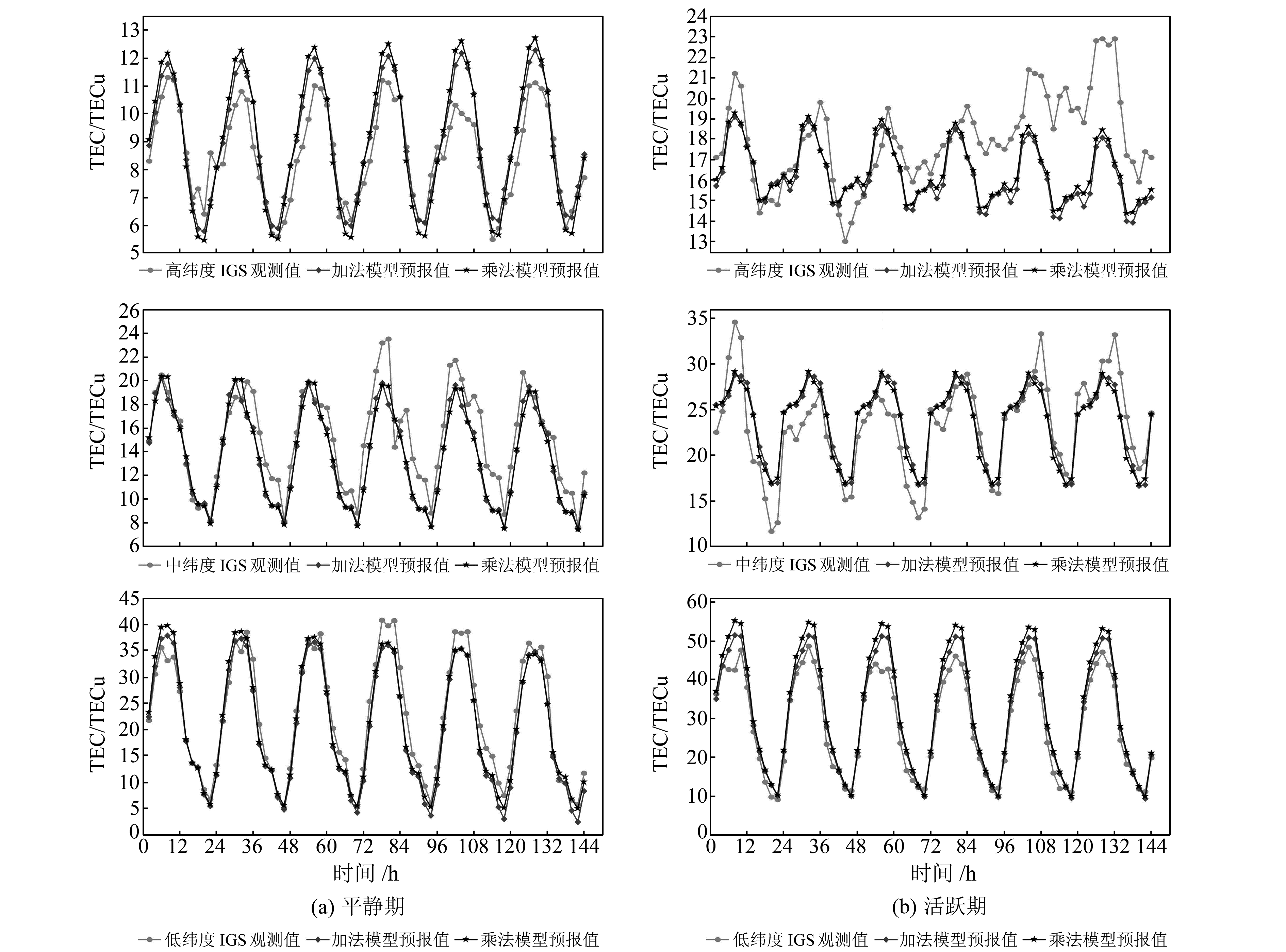
2.2 结果比较与分析利用2种模型对不同经纬度平静期、活跃期数据进行预报,图 1为预报结果与实际观测数据对比。可以看出,无论是在平静期还是在活跃期,2种模型的预报值在3个纬度地区均能较好地反映TEC变化特性。但与活跃期相比,平静期预报结果相对更好一些。
|
图 1 不同格网点平静期与活跃期TEC预报结果 Fig. 1 Prediction results of ionospheric TEC in different grid at quiet and active period |
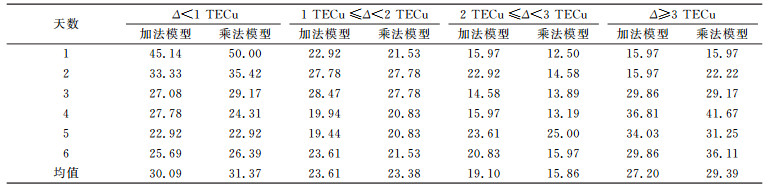
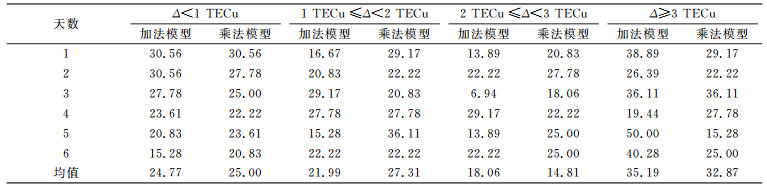
统计平静期、活跃期2种模型预测结果与实测数据之差的百分比得到表 1、表 2(单位%)。可以看出,在平静期,约30%的预报残差在1 TECu以内,约28%的预报数据残差大于3 TECu;在活跃期,约25%的数据预报残差在1 TECu以内,约36%的预报数据残差大于3 TECu。2种模型在平静期的预报残差相对优于活跃期。在平静期,加法模型预报残差在每个残差区间内所占百分比与乘法模型大致相同,约30%的预报残差在1 TECu以内,约30%的预报数据残差大于3 TECu。在活跃期,乘法模型预报残差在每个残差区间内所占百分比略优于加法模型,加法模型预报残差在1 TECu以内所占百分比与乘法模型大致相同,约为25%;加法模型预报残差介于1~2 TECu所占百分比约为22%,略低于乘法模型的27%;加法模型预报数据残差大于3 TECu所占百分比约为36%,比乘法模型低约3%。
|
|
表 1 电离层平静期预测残差分类统计 Tab. 1 Classification statistics of prediction residuals in ionospheric quiet period |
|
|
表 2 电离层活跃期残差分类统计 Tab. 2 Classification statistics of prediction residuals in ionospheric active period |
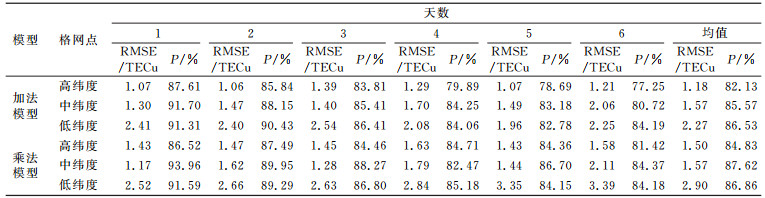
表 3为电离层平静期预报值的均方根误差和相对精度。由表 3可知,2种模型在不同纬度预报值的均方根误差和相对精度存在比较明显的差异。对于加法型模,预报值的相对精度随纬度的增加而降低,纬度越低,相对精度越高;均方根误差则随纬度的降低而增大,纬度越高,均方根误差越小。对于乘法模型,预报值的相对精度在中纬度地区最好,低纬度次之,高纬度最差;均方根误差亦随纬度的降低而增大,高纬度地区最小,中、低纬度依次增大。在相同纬度区域内,乘法模型预报值的相对精度略优于加法模型,加法模型预报值的均方根误差略优于乘法模型。
|
|
表 3 平静期预报值的均方根误差和相对精度 Tab. 3 RMSE and relative accuracy in ionospheric quiet period |
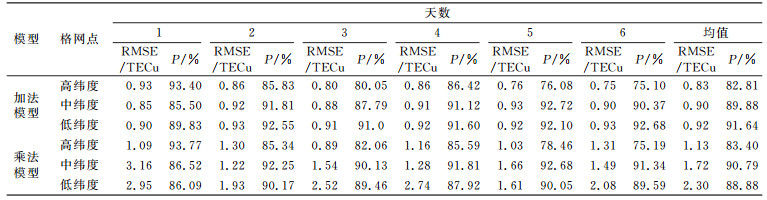
表 4给出了电离层活跃期预报值的均方根误差和相对精度。可以看出,2种模型在不同纬度预报值的均方根误差和相对精度有较大差异。对于加法型模,预报值的相对精度在低纬度最高,中纬度略差,高纬度最差;均方根误差在低纬度地区最大,中纬度略小,高纬度最小,但3者间的差异很小。对于乘法模型,预报值的相对精度在中纬度地区最好,低纬度略差,高纬度最差;均方根误差在低纬度地区最大,中纬度稍小,高纬度最小。在高纬度和中纬度地区,乘法模型预报值的相对精度略优于加法模型,在低纬度地区加法模型的相对精度略优于乘法模型;加法模型预报值的均方根误差在高、中、低纬度地区均优于乘法模型。
|
|
表 4 活跃期预报值的均方根误差和相对精度 Tab. 4 RMSE and relative accuracy in ionospheric active period |
结合表 3、表 4可以看出,无论活跃期还是平静期,在各纬度地区采用加法模型进行预报所得预报值的均方根误差均显著小于乘法模型,这主要是因为采用加法模型和乘法模型对TEC进行预报时,分解所得稳定成分、趋势成分和季节成分存在不同,对其进行预报重构,所得预报效果也存在差异。同时也说明,采用加法模型对TEC值进行预报,所得预报残差比较集中,不会出现大范围变化,预报结果比乘法模型能更好地吻合实际观测数据,反映电离层TEC的变化特性。
结合图 1、表 1~4可以看出,在平静期、活跃期虽有约30%预报残差大于3 TECu,却能得到较好的预报相对精度,主要是因为预报残差大于3 TECu主要集中在低纬度地区,低纬度地区受太阳辐射影响导致TEC值较大,且预报残差大于3 TECu的部分主要集中在4~5 TECu且在峰值附近,因此即使预报残差较大,也能得到较好的相对精度。
3 结语本文采用Holt-Winters加法模型和乘法模型对IGS中心提供的不同经纬度活跃期、平静期电离层TEC格网点数据进行短期预测,将预报值与IGS中心提供的观测值进行对比,得出结论:
1) 利用加法模型和乘法模型对电离层TEC值进行短期预报,所得预报结果与实际观测数据均吻合较好,但加法模型的预报结果能更好地反映电离层TEC的变化特性。
2) 在平静期,2种模型预报效果大致相同,加法模型预报值的均方根误差略优于乘法模型,乘法模型预报值的相对精度略优于加法模型;在活跃期,加法模型预报效果显著高于乘法模型,仅高纬度地区加法模型预报值的相对精度略低于乘法模型。
由于本文采用的数据有限,所得结论对其他区域是否适用还需进一步验证。
致谢: 感谢IGS中心提供实验数据!
| [1] |
Klobuchar J A. Ionospheric Time Delay Algorithm for Single Frequency GPS Users[J]. IEEE Trans Aerospace Elec Syst, 1987, 23(3): 325-331
(  0) 0) |
| [2] |
方涵先, 翁利斌, 杨升高. IRI、NeQuick和Klobuchar模式比较研究[J]. 地球物理学进展, 2012, 27(1): 1-7 (Fang Hanxian, Weng Libin, Yang Shenggao. The Research of IRI, NeQuick and Klobuchar Models[J]. Progress in Geophysics, 2012, 27(1): 1-7)
(  0) 0) |
| [3] |
蔡成辉, 刘立龙, 黎峻宇, 等. 基于改进的Klobuchar模型建立南宁市区域电离层延迟模型[J]. 大地测量与地球动力学, 2015, 35(5): 797-800 (Cai Chenghui, Liu Lilong, Li Junyu, et al. Establishment of Region Ionospheric Delay Model in Nanning Based on Improved Klobuchar Model[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 797-800)
(  0) 0) |
| [4] |
蔡成辉, 刘立龙, 黎峻宇, 等. 基于附有限制条件的多项式模型建立中国区域电离层模型[J]. 大地测量与地球动力学, 2015, 35(6): 1007-1011 (Cai Chenghui, Liu Lilong, Li Junyu, et al. Establishment of Region Ionospheric Delay Model in China Based on a Polynomial Model with Restrictive Conditions[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1007-1011)
(  0) 0) |
| [5] |
章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26 (Zhang Hongping, Ping Jinsong, Zhu Wenyao, et al. Brief Review of the Ionospheric Delay Models[J]. Progress in Astronomy, 2006, 24(1): 16-26 DOI:10.3969/j.issn.1000-8349.2006.01.002)
(  0) 0) |
| [6] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报:信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [7] |
汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报:信息科学版, 2013, 38(4): 404-411 (Tang Jun, Yao Yibin, Chen Peng, et al. Prediction Models of Ionospheric TEC Improved by EMD Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 404-411)
(  0) 0) |
| [8] |
席广永, 岳建平, 周保兴. 基于Holt-Winter的电离层延迟预报模型[J]. 测绘通报, 2012(9): 7-10 (Xi Guangyong, Yue Jianping, Zhou Baoxing. The Forecasting Model of Ionospheric Delay Based on Holt-Winter[J]. Bulletin of Surveying and Mapping, 2012(9): 7-10)
(  0) 0) |
| [9] |
陈艳红, 薛炳森, 李利斌. 利用神经网络预报电离层[J]. 空间科学学报, 2005, 25(2): 99-103 (Chen Yanhong, Xue Bingsen, Li Libin. Forecasting of Ionospheric Critical Frequency Using Neural Networks[J]. Chinese Journal of Space Science, 2005, 25(2): 99-103 DOI:10.3969/j.issn.0254-6124.2005.02.004)
(  0) 0) |
| [10] |
翁利斌, 方涵先, 缪子青, 等. 利用人工神经网络提前1 h预报电离层TEC[J]. 空间科学学报, 2012, 32(2): 204-208 (Weng Libin, Fang Hanxian, Miao Ziqing, et al. Forecasting of Ionospheric TEC One Hour in Advance by Artificial Neural Network[J]. Chinese Journal of Space Science, 2012, 32(2): 204-208)
(  0) 0) |
| [11] |
卢辰龙, 匡翠林, 张晋升, 等. 组合SSA与ARMA模型预报电离层TEC[J]. 大地测量与地球动力学, 2014, 34(6): 44-49 (Lu Chenlong, Kuang Cuilin, Zhang Jinsheng, et al. Predicting Ionosphere TEC with the Combination of Singular Spectrum Analysis and ARMA Model[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 44-49)
(  0) 0) |
| [12] |
张强, 章红平, 赵齐乐, 等. 利用最小二乘配置预报全球电离层总电子含量[J]. 大地测量与地球动力学, 2014, 34(6): 86-91 (Zhang Qiang, Zhang Hongping, Zhao Qile, et al. Global Ionospheric TEC Prediction Based on Least-Squares Collocation Method[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 86-91)
(  0) 0) |
| [13] |
吴涛, 颜辉武, 唐桂刚. 三峡库区水质数据时间序列分析预测研究[J]. 武汉大学学报:信息科学版, 2006, 31(6): 500-502 (Wu Tao, Yan Huiwu, Tang Guigang. Prediction on Time Series Analysis of Water Quality in Yangtze Reservoir Area[J]. Geomatics and Information Science of Wuhan University, 2006, 31(6): 500-502)
(  0) 0) |
| [14] |
吴越强, 吴文传, 李飞, 等. 基于鲁棒Holt-Winter模型的超短期配变负荷预测方法[J]. 电网技术, 2014, 38(10): 2810-2815 (Wu Yueqiang, Wu Wenchuan, Li Fei, et al. Ultra-Short Term Load Forecasting Using Robust Holt-Winters in Distribution Network[J]. Power System Technology, 2014, 38(10): 2810-2815)
(  0) 0) |
| [15] |
范成方, 史建民. 基于Holt-Winters及趋势ARMA组合模型的粮食种植成本预测分析--以山东玉米、小麦为例[J]. 中国农业资源与区划, 2014, 35(3): 45-51 (Fan Chengfang, Shi Jianmin. Analysis of Gran Production Cost Forecast Based on Holt-Winters and Trend ARMA Combined Model--Taking Corn and Wheat of Shandong Province for Example[J]. Chinese Journal of Agricultural Resources and Regional Planning, 2014, 35(3): 45-51)
(  0) 0) |
| [16] |
钱吉夫.SVR季节性时间序列预测模型的构建与应用[D].广州: 华南理工大学, 2010 (Qian Jifu.Modeling and Forecasting Seasonal Time Series Using Seasonal Support Vector Regression[D].Guangzhou: South China University of Technology, 2010)
(  0) 0) |
| [17] |
Holt C C. Forecasting Seasonal and Trends by Exponentially Weighted Moving Averages[J]. International Journal of Forecasting, 2004, 20(1): 5-10 DOI:10.1016/j.ijforecast.2003.09.015
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China;
3. College of Resources and Environment, Qinzhou University, 12 Binhai Road, Qinzhou 535000, China
 2017, Vol. 37
2017, Vol. 37