卫星导航系统定位方式按照接收机运动状态可分为静态定位和动态定位。动态定位比静态定位具有更广泛的应用前景,研究和优化单历元基线解算算法对于提高动态定位精度至关重要[1]。在模糊度已正确求解的条件下,若没有周跳,1个历元的观测数据就可以使短基线定位精度达到cm级。因此,正确探测周跳,快速准确地固定模糊度是单历元基线解算的核心[2-4]。
随着我国北斗卫星导航系统的建立与完善,BDS已具备为亚太地区提供较好定位服务的能力[5-6],但针对其高精度单历元解算算法的研究依然较少,尚无可利用的高精度动态解算软件。本文研究了北斗单历元动态定位后处理算法,并编制出北斗高精度动态后处理软件。利用该软件对国内中纬度某城市的变形监测数据进行处理,分析其精度与可靠性,并与Track解算的GPS数据结果进行对比。
1 基线解算原理 1.1 数学模型在单历元短基线相对定位中,通过差分能较好地削弱对流层延迟和电离层延迟的影响[7-10]。线性化后伪距及载波相位的双差观测方程为:
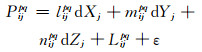
|
(1) |
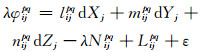
|
(2) |
式中,P为伪距观测值;φ为相位观测值;l、m、n分别为线性化后3个坐标分量的系数;dX、dY、dZ分别为基线向量3个方向的改正数;N为模糊度;L为常数项;下标i、j为测站;上标p、q为观测卫星。
根据卫星高度角定权,D▽△为双差观测量的协方差阵,P▽△为权阵:
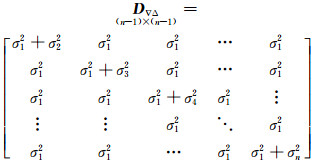
|
(3) |
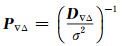
|
(4) |
式中,σp2为卫星p的单差观测量方差σp2=σi, p2+σj, p2;σi, p2为测站i观测卫星p的观测值方差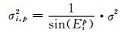
周跳会严重影响整周模糊度的解算,降低定位精度,因此首先要对其进行探测。本文同时利用MW组合与电离层残差组合(IRC)探测周跳:
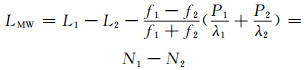
|
(5) |
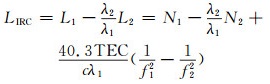
|
(6) |
式(5)为MW组合,LMW为观测值。若无周跳,历元间组合观测值即为2个频率上的模糊度之差。但是当L1、L2载波上同时出现1 :1的周跳时,无法探测出周跳。式(6)为电离层残差组合,LIRC为组合观测值。短基线电离层变化较小,若无周跳产生,则电离层残差组合值历元间连续;反之,历元间不连续时,即有周跳产生,但在电离层变化较大的时段会引入电离层的虚假误差。
因此,本文结合2种方法的优缺点,同时使用2种组合观测值探测周跳,若组合观测值在历元间不连续,则探测出周跳,增加1个模糊度变量。
1.3 模糊度解算本文使用模糊度空间搜索算法,共分为3步。
1) 确定初始搜索中心。
对式(5)、式(6)取双差联立得:
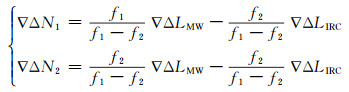
|
(7) |
遍历待求模糊度参数涉及的所有历元,取每个历元▽△LMW、▽△LIRC的平均值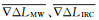
2) 确定搜索范围。
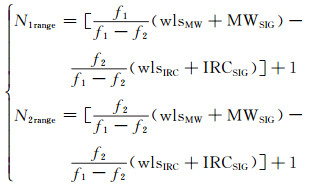
|
(8) |
式中,wlsMW、wlsIRC为LMW、LIRC模糊度的近似整数值与浮点值之差;MWSIG、IRCSIG为LMW、LIRC对应的RMS;[]表示取整,搜索范围为[-N1range, N1range]、[-N2range, N2range]。
3) 获得最佳候选值。
对模糊度搜索候选值进行组合作为模糊度搜索空间,将每个模糊度代入观测方程,取RMS最小的模糊度组合作为模糊度固定解。
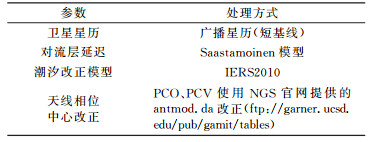
1.4 解算策略及流程GNSS定位精度不仅与卫星星历相关,也与数据处理过程中涉及误差消除和削弱的各种地球物理模型的精化相关。本文涉及的误差模型和策略详见表 1,流程见图 1。
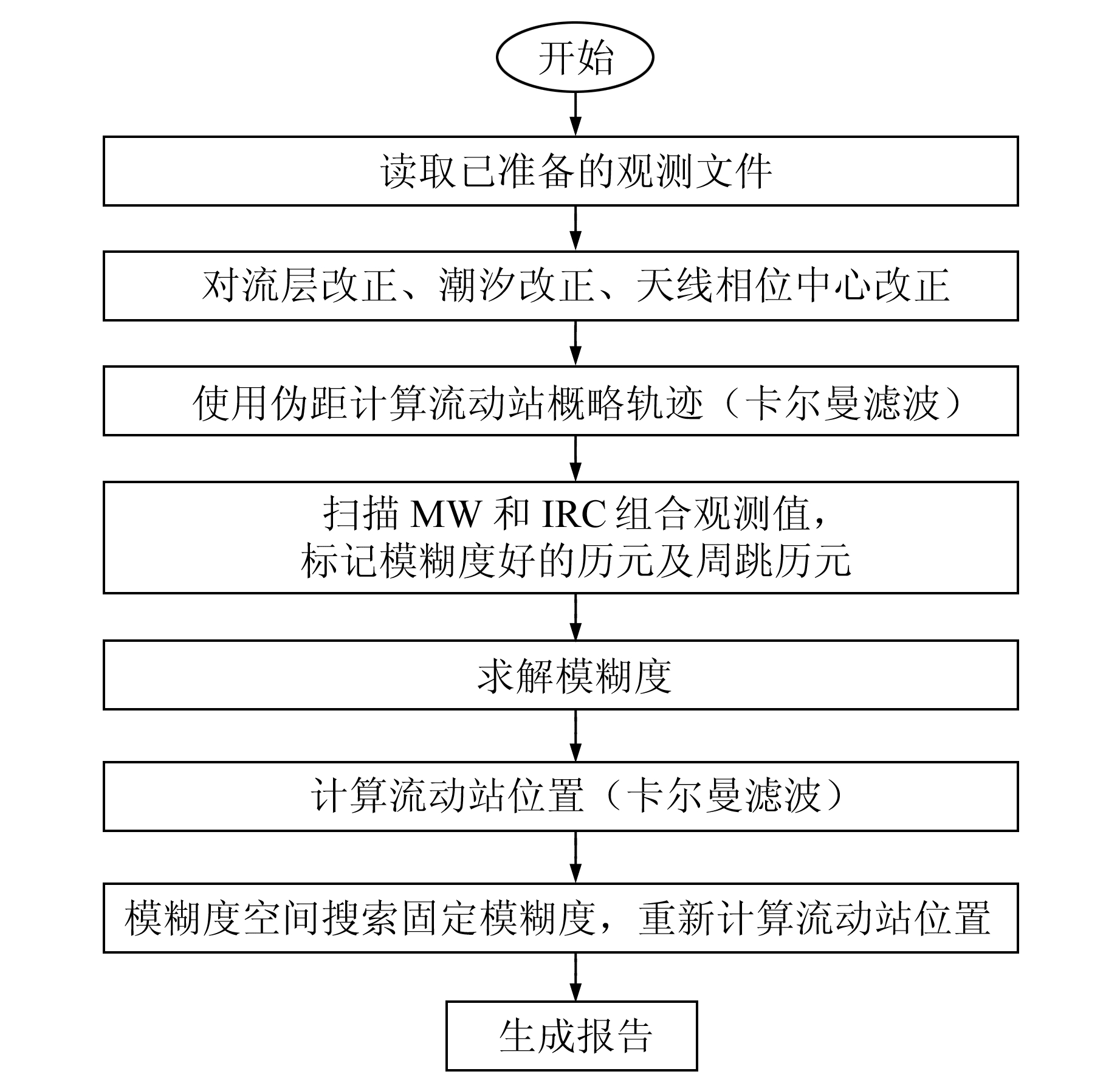
|
图 1 数据处理流程 Fig. 1 The flow diagram of data processing |
|
|
表 1 数据处理策略 Tab. 1 Data processing strategy |
为测试该软件解算北斗动态单历元数据的精度及可靠性,在国内中纬度某城市搭建变形监测平台并采集数据。图 2为实验观测网,基准站为JZ01,监测站为JC01、JC02、JC03、JZ02,基线长度均小于300 m。采集时间为2014-08~10,全天24 h不间断观测,采样间隔为15 s。采集过程中,接收机均采用TRIMBLE NETR9,天线均采用CHOKE RING(TRM59900.00),所有测站基本位于同一水平面上,仰角10°以上,没有遮挡。同时记录BDS和GPS观测数据,以便对2个系统观测数据分别进行解算。
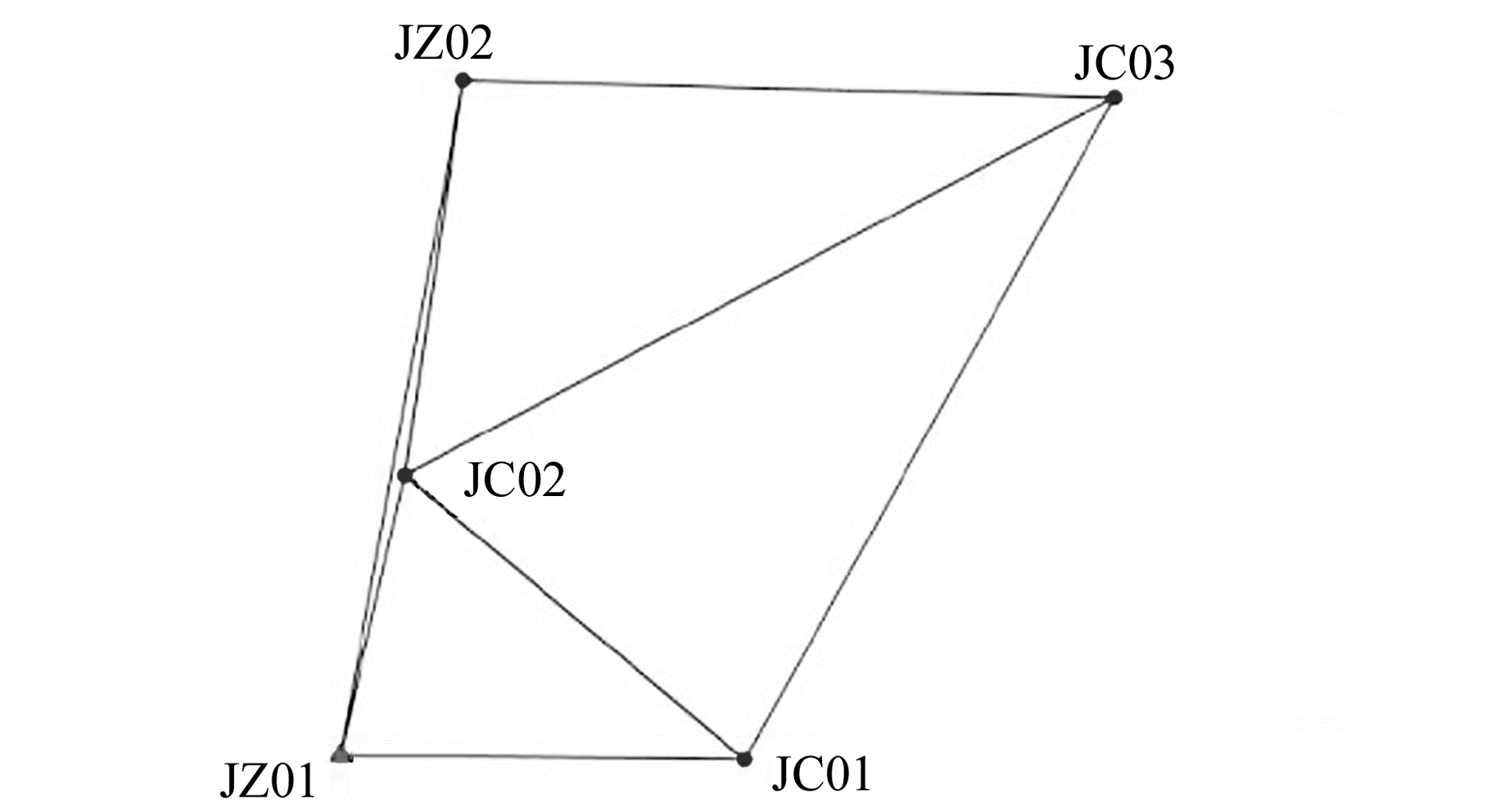
|
图 2 实验观测网网形 Fig. 2 Observation network |
统计JZ01站2014年第260天的可见卫星数及PDOP,截止高度角设为10°。图 3中实线表示可见卫星数逐历元的变化,虚线表示PDOP值逐历元的变化。图 4为对应的测站卫星天空图。由图 3、图 4可知,实验测站同时可见卫星达到7~13颗,共可观测到14颗卫星,包括5颗GEO卫星、5颗IGSO卫星以及4颗MEO卫星。卫星的PDOP值为1~4,大多数历元均小于2,说明测站的可视卫星数目足够,卫星的几何分布较好。

|
图 3 卫星数及PDOP值 |
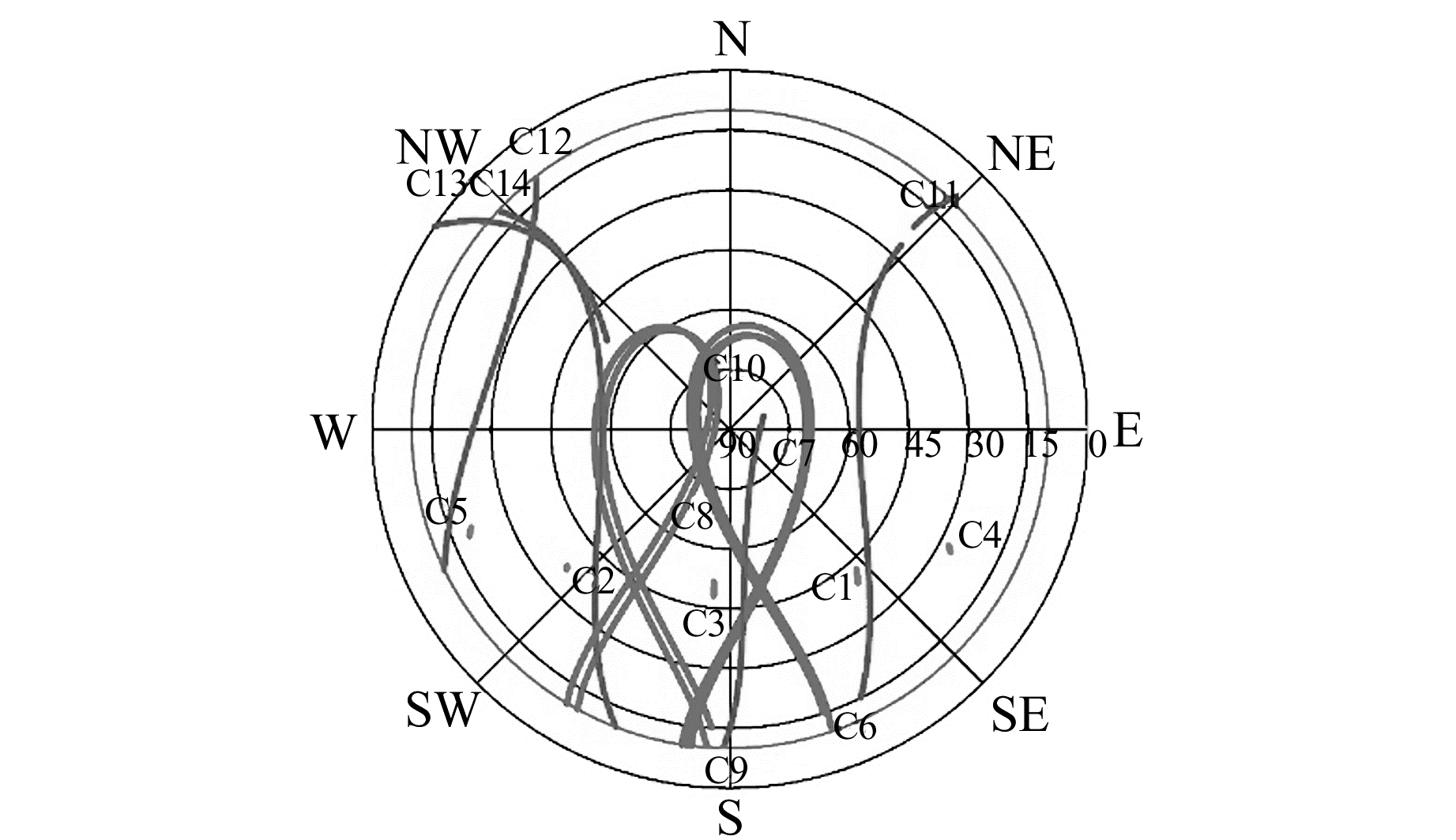
|
图 4 JZ01测站卫星天空图 Fig. 4 Satellite sky map of station JZ01 |
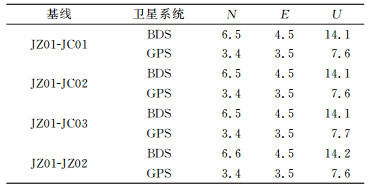
利用自编北斗单历元动态后处理软件对BDS数据进行处理,利用Track解算同时观测的GPS数据进行对比,数据处理结果均减去各分量的均值求得各测站各历元坐标残差序列。限于篇幅,仅给出2014-09-17(DOY=260)UTC 00:00~04:00 JC03站的结果,坐标分量的残差序列见图 5,各坐标分量的残差概率密度统计见图 6,坐标分量残差RMS统计见表 2(单位mm)。
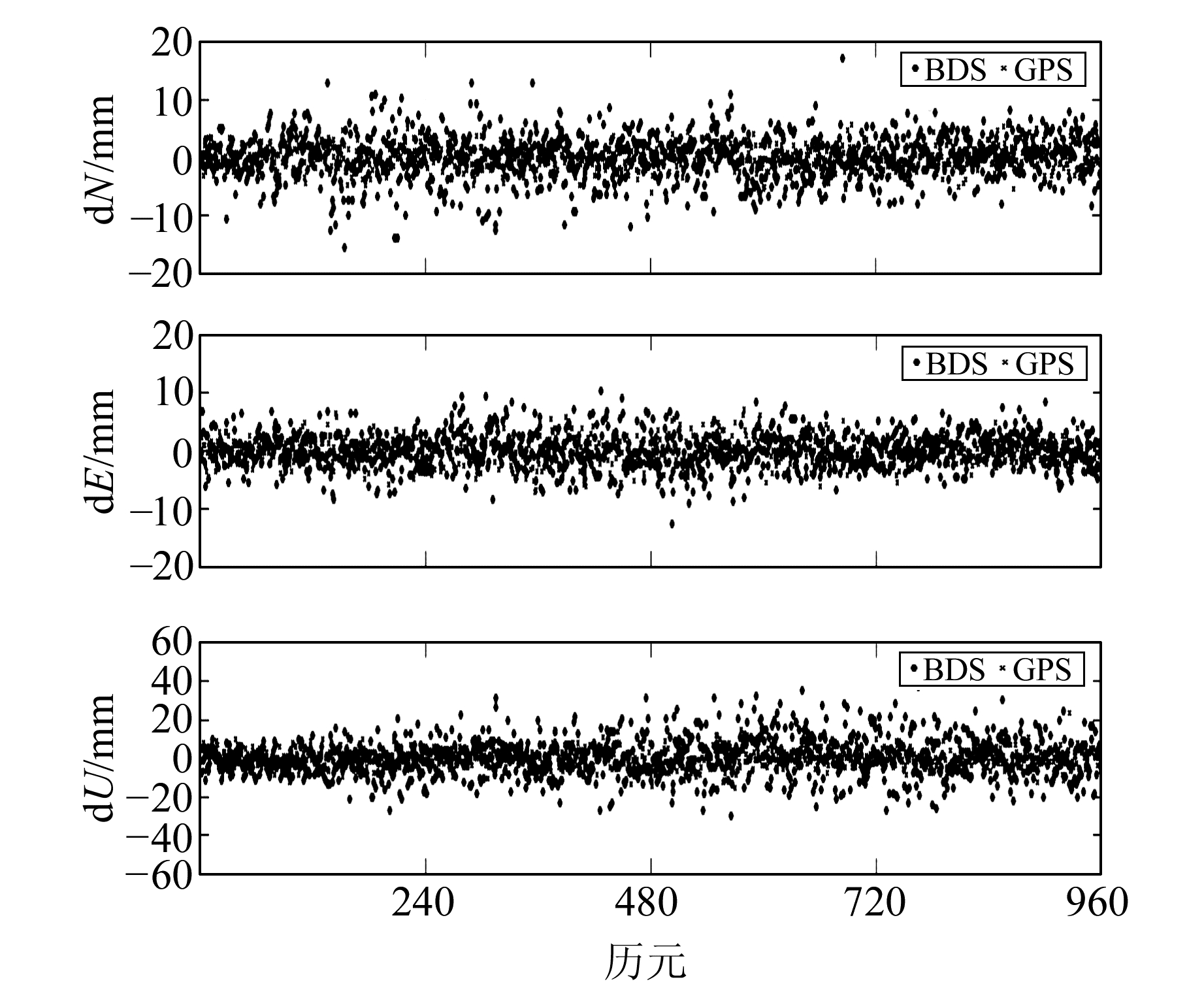
|
图 5 JC03-JZ01基线残差序列 Fig. 5 JC03-JZ01 baseline residual sequence |
|
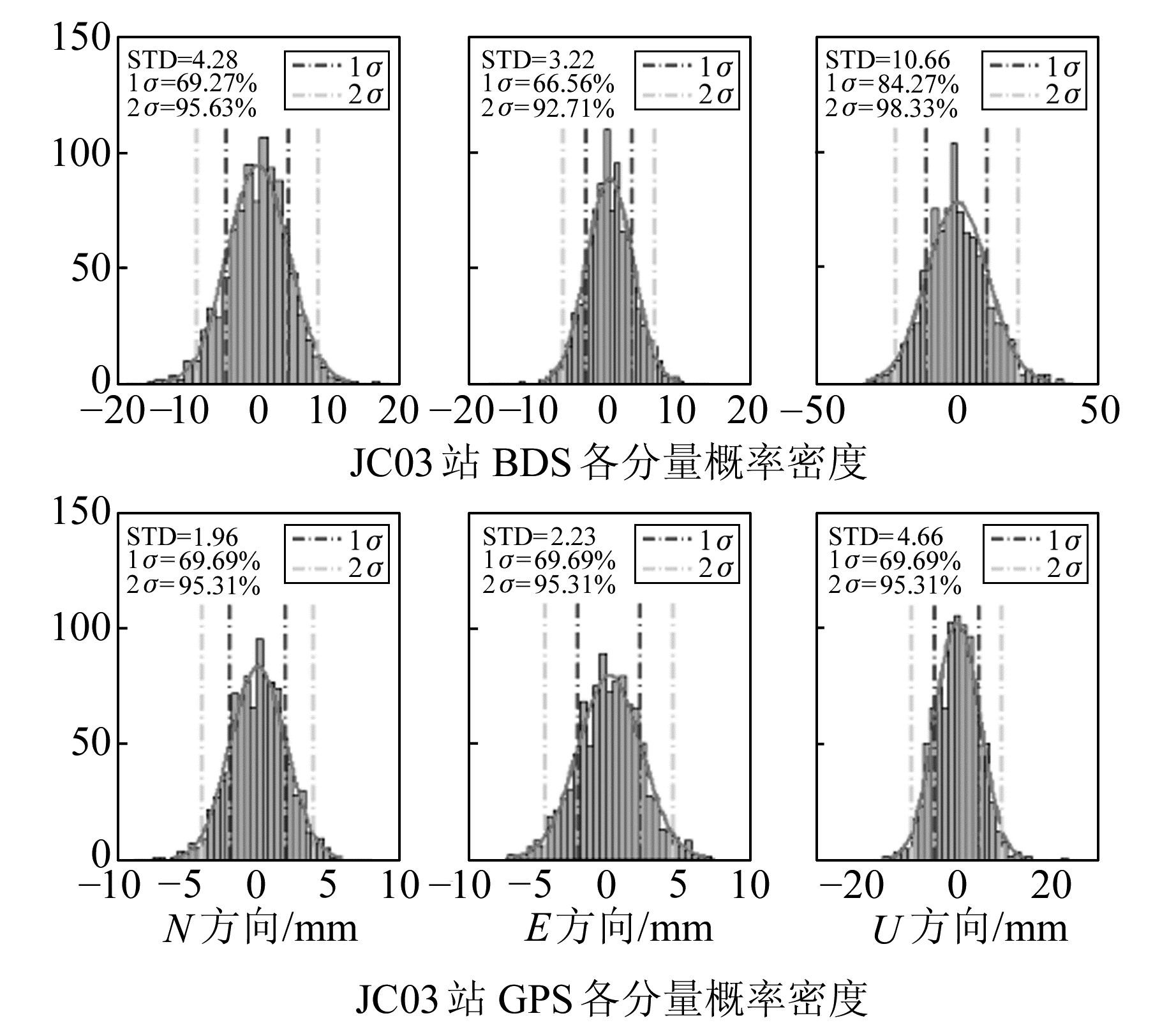
图 6 JC03-JZ01基线各分量概率密度统计 Fig. 6 Probability density of JC03-JZ01 baseline component |
|
|
表 2 坐标分量残差RMS统计表 Tab. 2 Residual RMS statistics of coordinate component |
从图 5可以看出,BDS和GPS的残差序列整体上都较为平稳。BDS观测值N、E方向的波动绝大部分都在10 mm以内,U分量波动大部分都在20 mm以内;GPS观测值N、E方向的波动绝大多数都在5 mm以内,U分量波动大部分都在10 mm以内。
从图 6可以看出,BDS和GPS各分量的坐标残差序列都近似满足正态分布。BDS的N方向和GPS的N、E、U3个方向的1σ和2σ符合度很高,BDS的E、U方向符合度不高;GPS各分量的STD均小于BDS。
从表 2可以看出,BDS所有测站的基线RMS值N和E方向不一致,E方向的4.5 mm优于N方向的6.5 mm,U方向优于15 mm; GPS的基线RMS值在N和E方向较一致,均优于3.5 mm,U方向优于7.6 mm。分析认为,BDS系统的RMS整体大于GPS,这种差距主要是因为BDS星座组网尚未完成,且系统误差尚未标定,随着BDS卫星星座的不断完善,其数据精度必定有大幅提高。单BDS数据处理结果各基线序列均表现为E分量结果最好,N分量次之,U分量最差,主要是由于BDS系统的卫星在东西方向上分布较均匀,南北方向分布不均匀,造成南北方向的卫星几何强度比东西方向差,因此对南北方向和垂直方向的精度造成一定的影响。
2.3 外符合精度分析为分析该算法的外符合精度,在测站JC03的底座上安装变形模具,可实现在水平和垂直方向上的移动来模拟变形。实验时间为2014-08-05(doy=217)和2014-08-10(doy=222),在第217天某时刻进行小尺度移动,N、E、U方向分别移动4 mm、2 mm、5 mm,在第222天某时刻仅U方向移动45 mm。
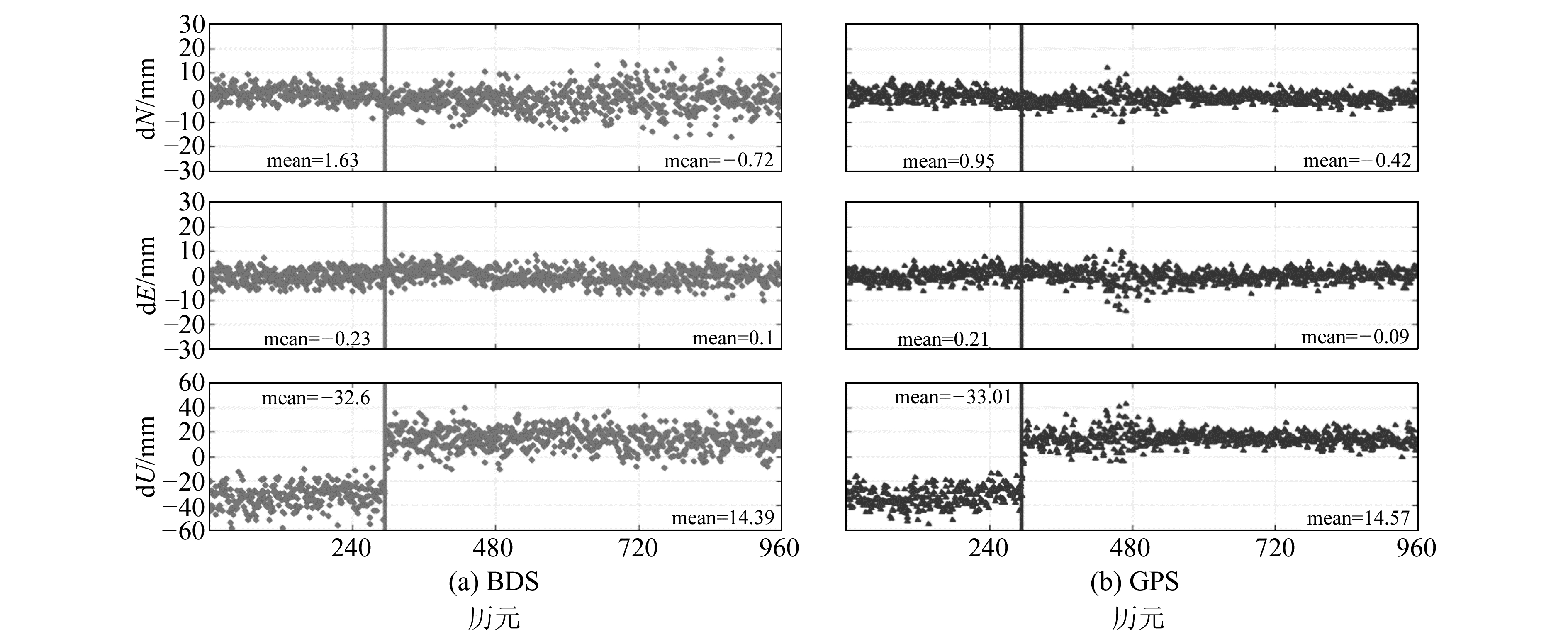
对变形实验数据进行单历元动态处理,观测时段依然为4 h,采样率为15 s,求得JC03的N、E、U 3个分量的残差序列,结果见图 7、图 8。图中竖线表示模具移动时刻,因第217天模具移动尺度较小,移动前后的变化在时间序列图中不易分辨,故计算出移动前后序列的平均值,在图中用mean标记。从图 7可以看出,在第217天,JC03测站水平方向上有微小移动,从移动前后的平均值可以看出,BDS解算得到的序列与移动的真值在N、E、U方向上分别相差0 mm、1 mm、0 mm;GPS解算得到的序列与移动的真值在N、E、U方向上分别相差0 mm、1 mm、0 mm。从图 8中可以看出,在第222天,JC03测站垂直方向上有较大移动,从移动前后的平均值可以看出,BDS、GPS解算得到的序列与移动的真值在U方向上均相差2 mm、3 mm。由此可见,该软件的外符合精度优于5 mm。

|
图 7 JC03第217天坐标分量变形序列 Fig. 7 JC03 coordinate component deformation sequence day of 217 |
|
图 8 JC03第222天坐标分量变形序列 Fig. 8 JC03 coordinate component deformation sequence day of 222 |
本文研究了北斗高精度单历元基线解算算法,开发了适用于北斗卫星导航定位系统的动态后处理软件。采集BDS和GPS同站观测数据,分析卫星可见性及PDOP值得出,目前我国中纬度地区的卫星数量及PDOP均满足基本定位需求。利用开发的BDS动态后处理软件和GAMIT的Track模块分别处理观测数据,对BDS和GPS在动态定位后处理的内符合精度和外符合精度进行分析得出,北斗N方向精度优于7 mm,E方向精度优于5 mm,U方向精度优于15 mm,北斗外符合精度优于5 mm。BDS动态数据解算内符合精度相比于GPS解算结果还有一定的差距,外符合精度与GPS相当。
| [1] |
He H B, Li J L, Yang Y X, et al. Performance Assessment of Single and Dual-Frequency Beidou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403 DOI:10.1007/s10291-013-0339-3
(  0) 0) |
| [2] |
喻国荣. 单历元模糊度解算问题[J]. 测绘通报, 2003(11): 6-7 (Yu Guorong. The Congenital Defect of GPS Single Epoch Ambiguity Resolution[J]. Bulletin of Surveying and Mapping, 2003(11): 6-7 DOI:10.3969/j.issn.0494-0911.2003.11.003)
(  0) 0) |
| [3] |
Deng C L, Tang W M, Liu J N, et al. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/Beidou System[J]. GPS Solutions, 2014, 18(3): 375-386 DOI:10.1007/s10291-013-0337-5
(  0) 0) |
| [4] |
苏小宁, 孟国杰, 胡丛玮, 等. 基于TRACK进行GPS单历元定位[J]. 大地测量与地球动力学, 2009, 29(3): 100-103 (Su Xiaoning, Meng Guojie, Hu Congwei, et al. Single Epoch GPS Positioning Based on Track Module[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 100-103)
(  0) 0) |
| [5] |
杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72-81 (Yang Yuanxi, Li Jinlong, Wang Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China:Earth Science, 2014, 44(1): 72-81)
(  0) 0) |
| [6] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [7] |
唐卫明, 邓辰龙, 高丽峰. 北斗单历元基线解算算法研究及初步结果[J]. 武汉大学学报:信息科学版, 2013, 38(8): 897-901 (Tang Weiming, Deng Chenlong, Gao Lifeng. Preliminary Results of Single Epoch Baseline Solution Based on Beidou Navigation Satellite System[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 897-901)
(  0) 0) |
| [8] |
禹信.GPS动态定位后处理软件研究[D].成都: 西南交通大学, 2013 (Yu Xin.Research on the Post-Processing Software of GPS Kinematic Positioning[D].Chengdu: Southwest Jiaotong University, 2013)
(  0) 0) |
| [9] |
席瑞杰, 肖玉钢, 刘邢巍. GPS变形监测中提取大变形量的单历元解算方法研究[J]. 大地测量与地球动力学, 2015, 35(1): 26-29 (Xi Ruijie, Xiao Yugang, Liu Xingwei. A Method of Single Epoch GPS Deformation Surveying to Obtain Large Deformation[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 26-29)
(  0) 0) |
| [10] |
Xi R J, Xiao Y G, Liu X W, et al.Feasibility Analysis of High-Precision Deformation Monitoring Using Beidou Navigation Satellite System[C].China Satellite Navigation Conference, Xi'an, 2015
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37