2. 西安测绘总站, 西安市西影路36号, 710054;
3. 解放军理工大学, 南京市海福巷1号, 210007
随着GNSS多频的发展, 许多接收机已具备接收双频数据的功能。采用单频模型削弱电离层延迟效果并不理想(如Klobuchar模型改正效果一般在60%左右[1]), 而双频观测量可以消除超过99%的电离层误差[2]。消电离层组合时, 对于卫星信号处理器到发射天线、接收机天线到信号输出这2个部分, 不同频点甚至同一频点不同码或相位存在硬件延迟。码延迟称为差分码偏差(differential code bias, DCB), 相位延迟称为未校正相位延迟(uncalibrated phase delays, UPD)。卫星端的DCB称为TGD(timing group delay), 接收机端的DCB称为IFB(inter-frequency bias)[3]。
采用双频观测量消电离层组合解算时, 对于接收机端的DCB, 由于单模单点定位各历元所有观测卫星信号在接收机端的硬件延迟一致, 因此该项将并入接收机钟差解算, 可忽略其对定位精度的影响; 对于卫星端的DCB, 同一历元下各卫星值不同, 由于卫星钟差已在平差前解算, 无法消除DCB的影响, 须予以改正。本文推导了BDS在SPP、PPP下码观测量为单频或双频时卫星端的DCB改正公式, 针对目前MGEX(multi-GNSS experiment)已经发播的BDS卫星端全年各天的DCB值, 利用实测数据分析该值对北斗伪距定位、静态精密定位、仿动态精密定位精度的影响。
1 研究现状及DCB值的分析硬件延迟可能给电离层观测值带来高达数m的系统误差, 甚至可能导致TEC出现负值, 是高精度TEC求解中最大的误差源。文献[4]详细推导了BDS中TGD和DCB在SPP和PPP下的改正公式, 并用实验分析了DCB对定位精度、接收机钟差、对流层延迟、模糊度值等的影响, 结果表明其在SPP、PPP下都会降低定位性能。
GPS广播星历和精密星历都采用L1频点的P1码和L2频点的P2码的双频无电离层组合的卫星钟差处理体系[4], 发布的DCB产品包括频内偏差P1C1、频间偏差P1P2、P1C2等。BDS钟差处理时广播星历基于B3频点的通道延迟偏差, 精密星历以B1、B2频点的消电离层组合作为基准[4]。消电离层组合时观测码要改正到钟差处理策略中的码进行解算。
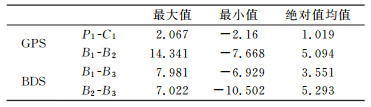
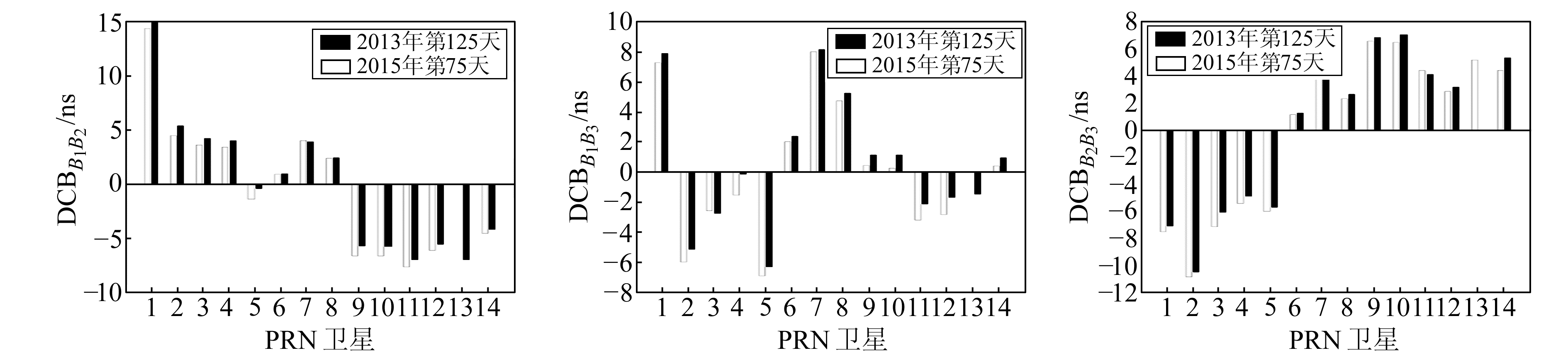
图 1为2013-05-05和2015-03-16 BDS中3个频点不同组合卫星端的DCB值。表 1(单位ns)统计了GPS、BDS的DCB值。从图 1和表 1看出, 相较于GPS, BDS卫星端DCB值大了4~6倍。GPS的P1C1绝对值在2 ns以内, BDS各个组合绝对值平均在4~6 ns, 个别甚至超过10 ns。BDS卫星端DCB值偏差较大, 对定位精度的影响也较大, 更应该考虑DCB所带来的定位误差。
|
图 1 BDS卫星端各频点间的DCB值 Fig. 1 The values of inter-frequency DCB of BDS satellite |
|
|
表 1 2015-03-16 DCB值数据统计 Tab. 1 Data statistics of DCB on March 16, 2015 |
导航系统的广播星历发播的TGD参数一般基于DCB值更新[4]。卫星钟差改正到时空参考点的原理是DCB对定位影响研究的理论基础, 本节首先分析GPS中TGD参数钟差的改正原理。
2.1 GPS系统TGD参数钟差改正原理以P1P2无电离层组合形成的PC为虚拟天线电子相位中心, 并记为导航卫星时空参考点。设P1、P2相对该参考点的时延为τ1、τ2, 对应频率为f1、f2, δts为卫星钟差, 则经PC组合处理后的卫星钟差dtSV为[5]:
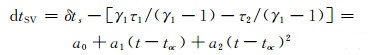
|
(1) |
式中, γ1=f12/f22, a0、a1、a2为由广播星历播发的卫星钟改正数。该式即为GPS发布的卫星钟差处理公式。GPS广播星历中定义的dTGD参数为:

|
(2) |
因此, 可以得到单频P1、P2码钟差改正公式为:
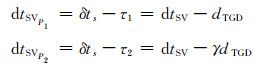
|
(3) |
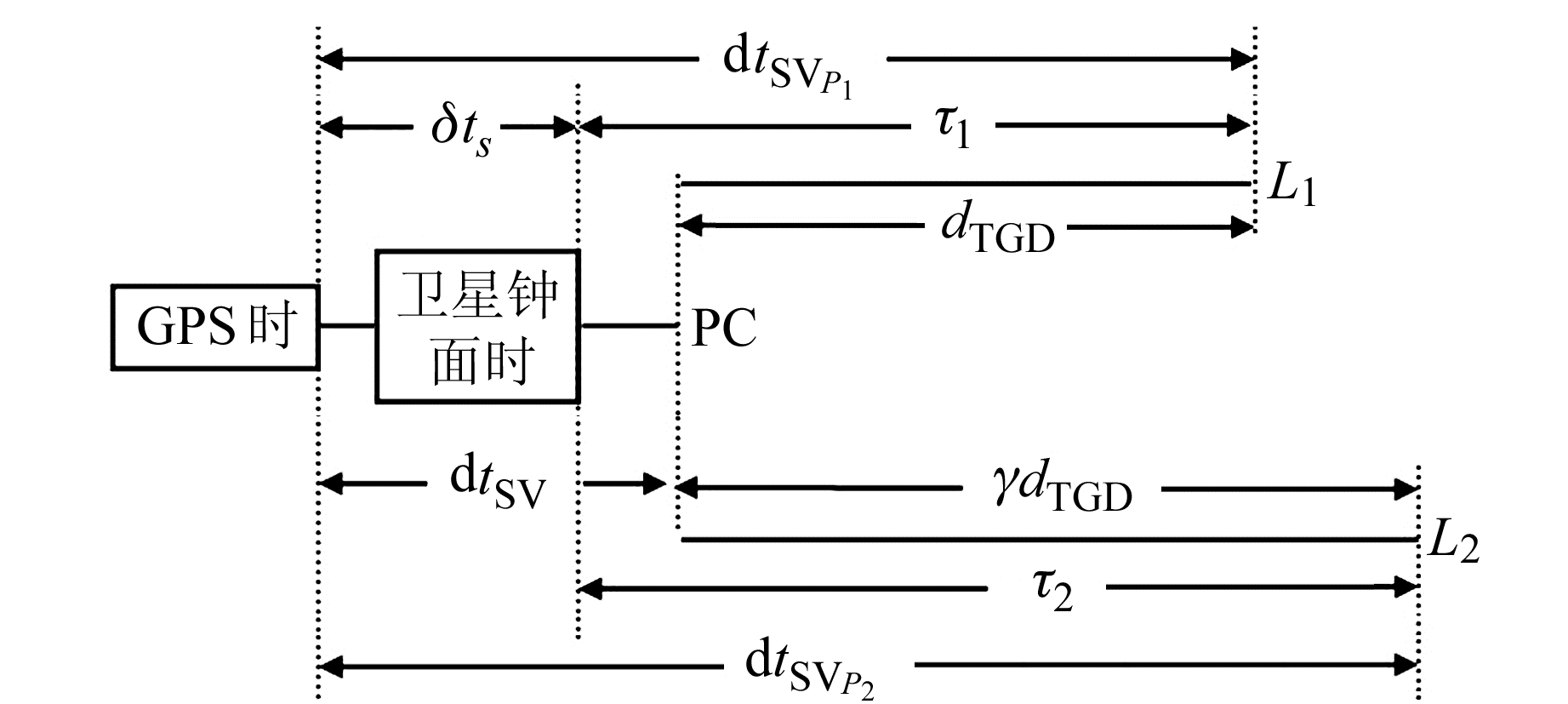
卫星钟差δts、PC组合后卫星钟差dtSV及dtSVP1、dtSVP2的关系见图 2。
|
图 2 GPS钟差参数改正原理 Fig. 2 The principle of GPS satellite clock bias parameter |
伪距定位观测方程为:
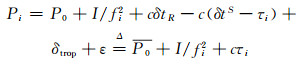
|
(4) |
式中, Pi为第i频点实测伪距, P0为对应星地几何距离, I为观测历元电离层改正延迟, fi为频率, δtR、δtS为测站及卫星钟差, δtrop为对流层误差, ε为伪距观测误差, 包含多路径效应, c为光速, τi为第i频点卫星端硬件延迟误差。
由P1P2码消电离层组合可得PC=(P2-γ1P1)/(1-γ1)。把P1归算到PC, 2者相减, 有P1-PC=(P1-P2)/(1-γ1)[6], 即

|
(5) |
令TGD=cdTGD, 则P1码改正到PC组合下的公式为:

|
(6) |
GPS系统TGD参数钟差改正原理见图 2。
2.2 BDS系统DCB改正原理BDS广播星历中以B3频点的B3码作为基准硬件延迟偏差, 设τi为Bi频点下Bi码的星上链路发射延迟, ICD文件中定义的2个TGD参数为[7]:
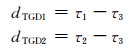
|
(7) |
同样假设Bi代表码伪距, 由§2.1推导可得B1、B2单频用户归算到B3时空参考点的码改正公式为:
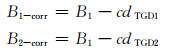
|
(8) |
分析B1、B3双频用户的延迟改正, 令α=f12/f22, β=f12/f32, γ=f22/f32, 则:
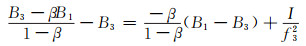
|
(9) |
式中, I/f32并不含在码组合项中, 这是B3频点下单频定位的电离层延迟项, 改正时不应加上这项改正。因此改正公式为:
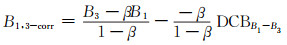
|
(10) |
式中, DCBBi-Bj表示Bi和Bj之间的码延迟, 该值可由MGEX提供的bsx文件获取。
分析B2B3、B1B2的双频组合可以得到类似结论。总结SPP下码的DCB改正公式为:

|
(11) |
式中, Bi均为码伪距观测量, 将其代入式(4)便可得DCB改正后的观测方程。
BDS精密星历中, 钟差解算基于B1B2消电离层组合定义的时空参考点[4]。选取B1、B3码作为观测量, 组合码相减, 有:
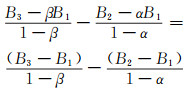
|
(12) |
可得改正公式为:
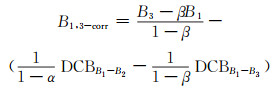
|
(13) |
同样方法可得其他频点码改正公式。总结PPP下码的DCB改正公式为:

|
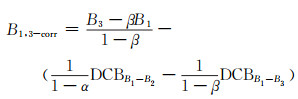
|
(14) |

|
选取2013-05-05 iGMAS测站BJF1和SHA1、2015-03-16 MGEX测站CUT0和JFNG的24 h静态观测数据, 数据采样间隔30 s。GPS定位中码观测量为C1、P2, BDS中码观测量为B1、B2、B3。DCB文件均为MGEX播发的天DCB值, 截止高度角取15°。测站真实坐标由CSRS-PPP解算得到[8]。
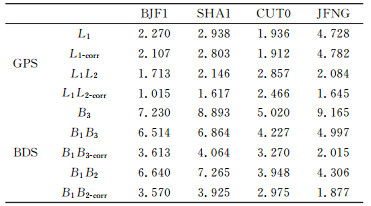
GPS、BDS定位结果RMS的统计见表 2(单位为m), 其中L1-corr为C1码改正到P1码的结果, BDS系统给出了B1B2码和B1B3码消电离层组合定位结果。B2B3组合无法输出解算结果, 在此并未列出, 主要原因是该组合噪声放大因子达到14.3, 而另外2个频点仅为2~3。图 3(a)为JFNG SPP 3个方向的结果。
|
|
表 2 伪距定位解算结果RMS Tab. 2 Root mean squares of SPP solutions |

|
图 3 BDS DCB改正定位结果 Fig. 3 BDS epoch-wise results of DCB experiments |
1) GPS卫星端DCB改正后定位精度改善在dm级, DCB改正与否双频模式相比单频模式精度都有提高。
2) B1B2组合、B1B3组合DCB改正后精度改善1~3 m, 精度提高50%左右; 观测质量差时, DCB改正后仍保持精度稳定, 尤其B1B2组合JFNG测站U方向, 改正前精度达20 m, 改正后定位精度保持5 m以内。总体上E方向精度改善在dm级, N、U方向精度改善在m级。
3) GPS中PC组合较单频定位精度更高, 而BDS中, E、N方向改正前的PC组合精度低于单频精度。文献[9]通过多个测站实验指出, 北斗广播星历的TGD参数存在问题, PC组合比单频精度差。考虑到BDS各卫星DCB值的大小, 初步分析是DCB值过大造成的。
3.2 PPP模式仅取§3.1中MGEX测站的观测文件, 截止高度角取15°, 对流程干延迟采用模型估计, 湿延迟作为待估计量, 海潮改正blq文件采用FES2004模型, GPS卫星端atx文件为对应精密星历的周文件, BDS尚未发布接收机端PCO产品, 在此并未考虑, 卫星端PCO改正取MGEX提供的值(0.6 m, 0 m, 1.1 m), 对GPS、BDS进行静态及仿动态PPP解算。由§3.1可知, B2B3频点组合噪声因子过大, 无法定位, 只对B1B3组合解算。由于JFNG测站BDS观测数据质量较差, 其仿动态后半段历元已剔除。表 3为静态最终收敛值与真实值的差值, 表 4为仿动态所有历元的RMS。图 3(b)、图 3(c)分别为CUT0静态和JFNG仿动态结果。
|
|
表 3 静态PPP最终收敛与真实坐标差值 Tab. 3 The difference between PPP-static results and real value |
|
|
表 4 仿动态PPP解算结果RMS Tab. 4 Root mean squares of epoch-wise PPP results |
1) GPS静态DCB改正后加快了收敛, 最终改正为mm级; 动态中精度改善在cm~dm级, 精度提高在10%~80%, 尤其JFNG测站E方向, 精度提高了80%。可见DCB在PPP的处理中是一个很重要的误差项。
2) BDS中静态、动态下改正后, 与钟差处理时空参考点B1B2组合定位结果基本一致, 证明了改正公式的正确性。CUT0仿动态下改正后精度反而更差, 几项mm~cm级精度的误差项并未改正, 其原因是动态下误差无法收敛, 造成定位结果受同等量级其他误差项的影响。
3) 相较于BDS, GPS精度改善更明显, 其原因是GPS各项误差改正较好, 卫星端PCV、接收机端PCO都已改正, 另外C1P1码为频内改正, 不涉及频率处理。
4 结语由于DCB的存在, 在卫星端必须假定1个时空参考点进行卫星钟差参数改正。文中基于卫星钟差参数改正原理推导了BDS两种定位模式下DCB单频及双频组合观测量改正公式。
2种定位模式下精度改善明显, 尤其BDS伪距定位由于DCB值较大, 改正前E、N方向定位精度比单频差, 而且放大了噪声, 严重影响定位精度。PPP中静态下GPS、BDS收敛精度改善在mm~cm量级, 动态下GPS精度改善在cm~dm量级。
致谢: 感谢全球连续监测评估系统(iGMAS)信息工程大学分析中心的帮助和支持。
| [1] |
章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26 (Zhang Hongping, Ping Jinsong, Zhu Wenyao, et al. Brief Review of the Ionospheric Delay Methods[J]. Progress in Astronomy, 2006, 24(1): 16-26 DOI:10.3969/j.issn.1000-8349.2006.01.002)
(  0) 0) |
| [2] |
Wilson B D, Yinger C H, Feess W A, et al. New and Improved——the Broadcast Inter-Frequency Biases[J]. GPS World, 1999, 10(9): 56-66
(  0) 0) |
| [3] |
樊家琛, 吴晓莉, 李宇翔, 等. 基于三频数据的北斗卫星导航系统DCB参数精度评估方法[J]. 中国空间科学技术, 2013, 33(4): 62-70 (Fan Jiachen, Wu Xiaoli, Li Yuxiang, et al. COMPASS Satellites DCB Parameter Accuracy Assessment Based on Tri-Frequency Data[J]. Chinese Space Science and Technology, 2013, 33(4): 62-70)
(  0) 0) |
| [4] |
Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5): 427-445 DOI:10.1007/s00190-015-0788-2
(  0) 0) |
| [5] |
戴伟, 焦文海, 贾小林. Compass导航卫星频间偏差参数使用方法[J]. 测绘科学技术学报, 2009, 26(5): 367-369 (Dai Wei, Jiao Wenhai, Jia Xiaolin. Application Research for Compass Navigation Satellite Interfrequency Bias Correction Terms[J]. Journal of Geomatics Science and Technology, 2009, 26(5): 367-369 DOI:10.3969/j.issn.1673-6338.2009.05.015)
(  0) 0) |
| [6] |
魏传军.基于地基GNSS观测数据的电离层延迟改正研究[D].西安: 长安大学, 2014 (Wei Chuanjun. Study of Ionospheric Delay Correction Based on GNSS Observations[D]. Xi'an: Chang'an University, 2014) http://www.bigengculture.com/kejilunwen/dizhicehuilunwen/2182391.html
(  0) 0) |
| [7] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号(2.0版)[Z].北京, 2013 (China Satellite Navigation Office.Beidou Navigation Satellite System Signal in Space Interface Control Document-Open Service Signal, Version 2.0[Z].Beijing, 2013)
(  0) 0) |
| [8] |
李黎, 王潜心, 李旋, 等. CSRS-PPP在线定位服务系统精度分析[J]. 城市勘测, 2008(5): 70-72 (Li Li, Wang Qianxin, Li Xuan, et al. Precision Analysis of CSRS - PPP On-Line Service System[J]. Urban Geotechnical Investigation & Surveying, 2008(5): 70-72 DOI:10.3969/j.issn.1672-8262.2008.05.017)
(  0) 0) |
| [9] |
吴静, 段志强. GPS与北斗广播星历TGD参数对单点定位影响比较分析[J]. 湖北民族学院学报:自然科学版, 2015, 33(1): 109-113 (Wu Jing, Duan Zhiqiang. The Impact of GPS and BDS Broadcast TGD on Single Point Positioning[J]. Journal of Hubei University for Nationalities:Natural Sciences, 2015, 33(1): 109-113)
(  0) 0) |
2. Xi'an Division of Surveying and Mapping, 36 Xiying Road, Xi'an 710054, China;
3. PLA University of Science and Technology, 1 Haifu Lane, Nanjing 210007, China
 2017, Vol. 37
2017, Vol. 37