GNSS接收机为每个导航卫星信号设计了1个通道[1], 因此当采用不同制造商生产的接收机进行RTK解算时, 就会造成接收机内部通道频间偏差(inter-frequency biases), 这些时间变量会对伪距观测量和载波观测量产生一定的影响。研究表明, 接收机内部频间偏差包含1个常数项和1个与频点相关的变量2个部分, 通过组双差的形式, 可以消除常数项, 而频点相关部分会与接收机钟差项混合在一起[2]。对于BDS而言, 由于其信号采用的是CDMA体制, 即使采用不同制造商生产的接收机对, 频点相关部分通过组双差也可消除; 而对于GLONASS, 只有采用相同的接收机对, 这部分偏差在组双差之后才能忽略, 否则将会严重影响模糊度解算的成功率[3]。
1 GLONASS/BDS联合RTK定位 1.1 时空基准统一BDS时间基准采用北斗时(BDT), 与GPS时间系统(GPST)间存在14 s的整数差。BDT与中国维持的协调世界时UTC(NTSC)之间的关系式为[4-5]:
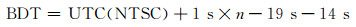
|
(1) |
GLONASST属于UTC时间系统, 与俄罗斯维持的协调世界时UTC(SU)存在3 h的整数差。GLONASST与UTC(SU)的关系式为:
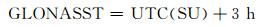
|
(2) |
将UTC作为中间变量, 可实现BDS、GLONASS时间系统的统一。
PZ90.02与ITRF2000只存在原点的平移, 3个轴的定向与ITRF一致。PZ90.02与ITRF2000的转换关系为:
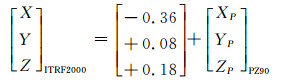
|
(3) |
CGCS2000定义为ITRF97, 采用2000.0历元下的坐标和速度场。CGCS2000与PZ90都与ITRF存在一定的关系, 它们之间的转换本质上是在不同的ITRF框架间实现统一。
1.2 定位模型在短基线(小于10 km)条件下, 忽略双差对流层残差、双差电离层残差以及轨道误差的影响, 载波和伪距单频差分定位的数学模型为[2]:
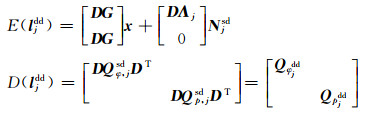
|
(4) |
式中, sd表示单差; dd表示双差; Λj= 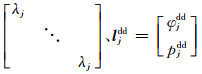
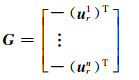
|
(5) |
单差模糊度参数到双差模糊度参数的转换矩阵为:

|
(6) |
短基线情形下的单频差分定位数学模型相应的未知参数向量为Y′ =[(Δrqr)T (Njsd) T]T, 即为位置参数和单差模糊度参数。
本文组双差是在各个系统内部实现的, BDS与GLONASS之间不组双差。之所以采取这样的解算策略, 是因为对于不同的导航系统, 即使具有相同波长的载波信号也会存在不同的群延迟, 无法通过组双差进行消除。如果这部分系统间系统误差处理不好, 反而会降低定位结果的精度。双差模糊度浮点解到固定解的计算采用LAMBDA算法, ratio的阈值设为2.0。解算过程中采用单历元模糊度固定模式。
2 GLONASS频间偏差修正方法频间偏差的影响可以通过事先标定的方法进行修正, 以提高双系统联合RTK定位模糊度固定的成功率和可靠性。通常, 可通过零基线解算得到载波相位以及伪距观测量的频间偏差修正值。当采用不同制造商生产的GNSS接收机进行相对定位时, 顾及GLONASS频间偏差造成的影响, 短基线条件下的观测方程为[2]:
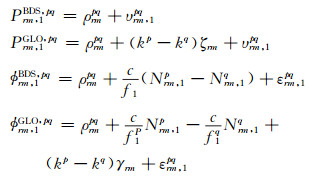
|
(7) |
式中, 假定同一颗卫星上2个载波频率的偏差值是相同的, 并且该偏差对于不同卫星是频率相关的[3]; m、r分别为基准站和用户流动站上的接收机; p、q为观测卫星; ϕrm, 1BDS, pq和ϕrm, 1GLO, pq分别为BDS、GLONASS两个系统L1载波观测量的双差形式(单位m); Prm, 1BDS, pq和Prm, 1GLO, pq分别为2个系统L1伪距观测量的双差形式(单位m); ζrm和γrm分别为伪距观测量和载波相位观测量的频间偏差值; kp和kq为GLONASS卫星的频率通道号, 取值为[-7, 6]; υrm, 1pq和εrm, 1pq分别为伪距观测量和载波观测量的观测噪声。
零基线条件下, 几何相关项ρrmpq等于0。对于伪距观测量而言, 双差之后的余项含有频间偏差ζrm和噪声υrm, 1pq; 而对于载波观测量, 双差余项中除频间偏差和噪声外, 还含有模糊度参数Nrm, 1p和Nrm, 1q。下面将分别就2种观测量频间偏差的求解进行研究。
2.1 伪距观测量频间偏差修正方法ζrm和υrm, 1pq同为dm量级, 因此不能忽略υrm, 1pq直接求解ζrm。这里提出一种求解策略:(kp-kq)ζrm+υrm, 1pq中, 选择kp-kq的绝对值较大的情况, 如±10, 将ζrm项进行放大, 一定程度上可降低噪声υrm, 1pq在双差余项中的影响权重, 进而忽略噪声υrm, 1pq, 直接求解ζrm。
2.2 载波相位观测量频间偏差修正方法载波相位观测量的噪声水平为mm量级, 而γrm为cm量级。因此, 忽略噪声项的影响, 只要求解出模糊度参数Nrm, 1p和Nrm, 1q, 就可得到γrm的值。而与之矛盾的是, 想要得到模糊度参数, 又必先求得γrm。采用如下策略进行解算:由于原始载波波长约为20 cm, 因此, 这里选择γrm的系数(kp-kq)绝对值较小的情况(理论上最小为±1, 文中设为±1), 使得(kp-kq)γrm对模糊度参数的影响小于载波观测量的半个波长(10 cm), 并设定Nrm, 1q等于0[3], 通过直接取整得到Nrm, 1p的整数解, 然后将其回代入双差方程中, 得到γrm的初值; 将该初值代入到其他(|kp-kq|≠1)双差观测方程中, 通过取整得到单差模糊度的固定解。至此, 所有的模糊度参数都固定完毕。最后, 解算得到n个γrm值(n为双差方程个数), 将这n个γrm值取平均数, 得到该历元γrm的最终解算值。
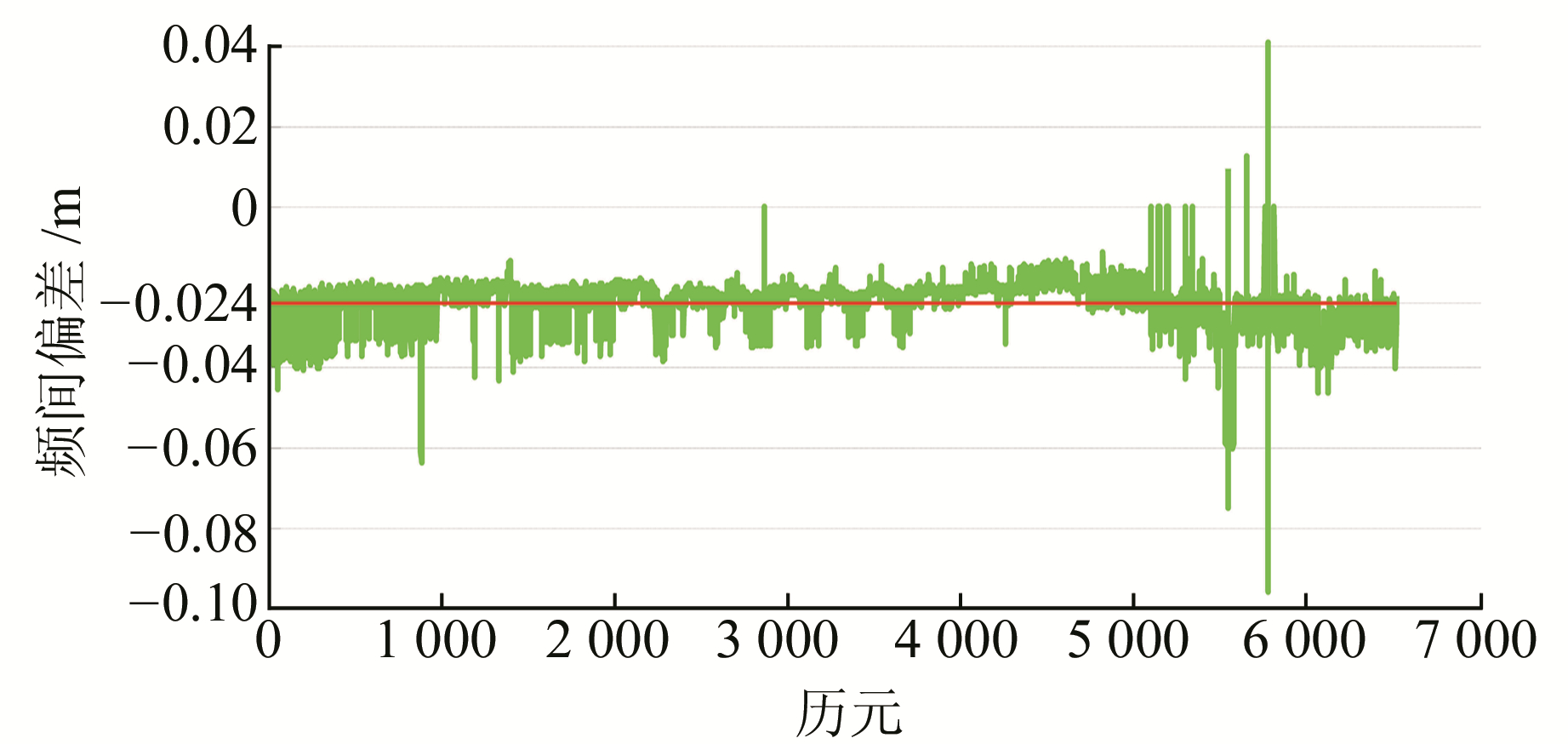
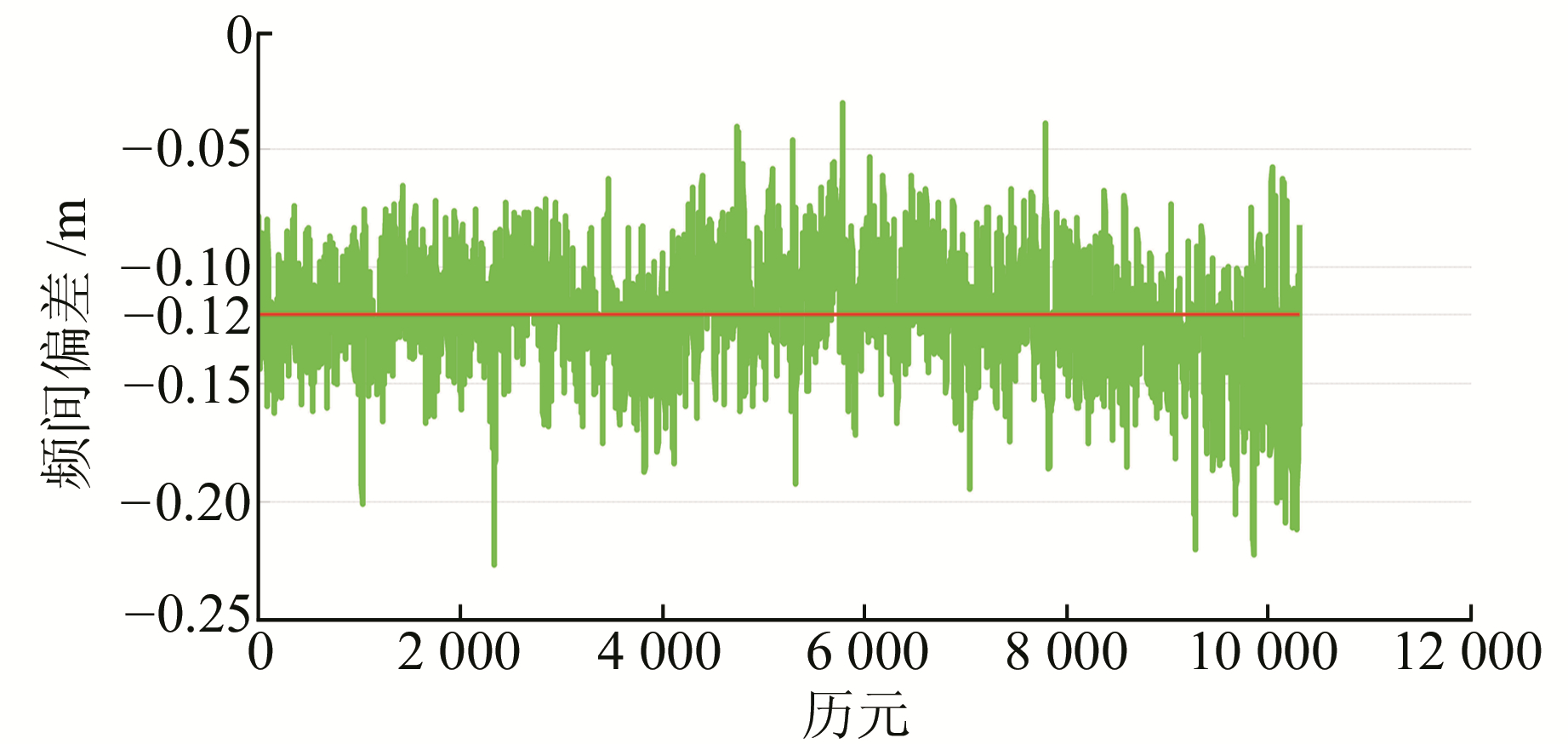
3 实验分析采用一条11 m的超短基线和一条8 km的短基线进行实验。分别采用思南、和芯星通2种多模接收机, 观测时长均为2 h, 采样间隔为1 s。验证之前, 先进行零基线数据的采集, 数据时长为3.5 h, 采样间隔为1 s。通过零基线解算得到频间偏差校正值, 如图 1、图 2所示。
|
图 1 载波相位频间偏差 Fig. 1 Carrier phase inter-channel bias |
|
图 2 伪距频间偏差 Fig. 2 Pseudorange inter-channel bias |
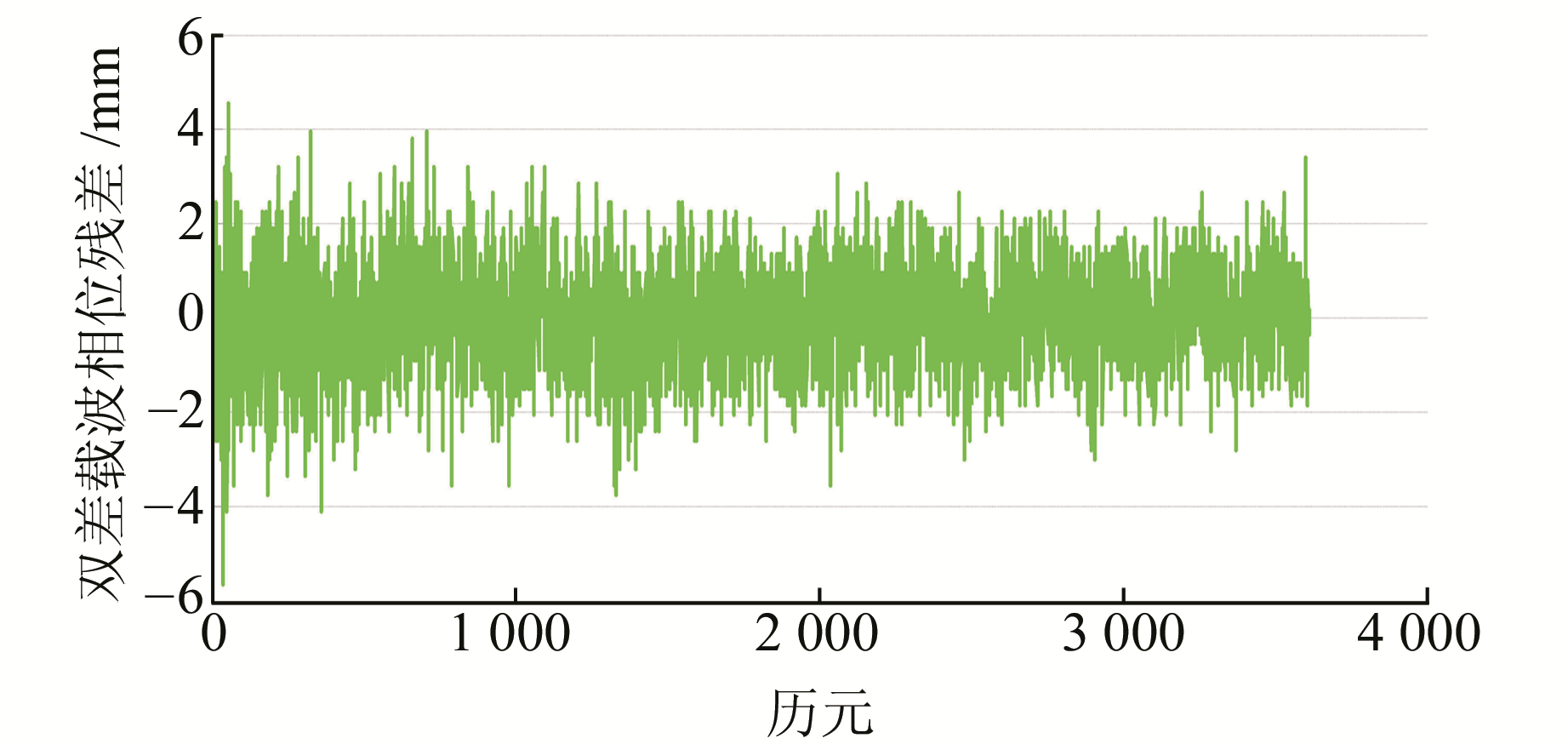
对所有历元取平均值, 得到ζrm和γrm的修正值分别为-0.024 m和-0.120 m(红线所示)。选取其中1组卫星对, 其修正之后载波相位和伪距的双差残差如图 3、图 4所示。
|
图 3 双差载波相位残差 Fig. 3 Double-differenced bias of carrier phase |
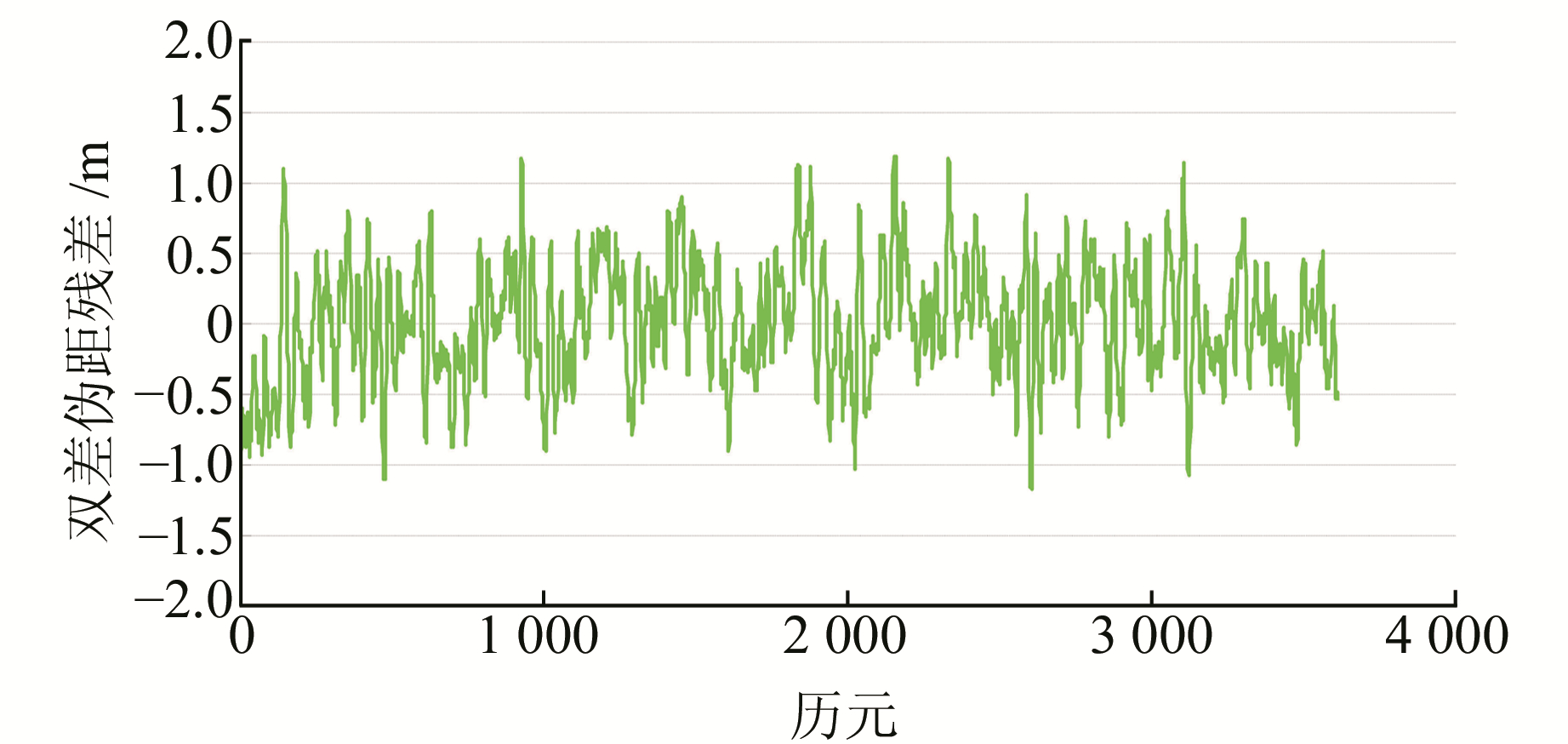
|
图 4 双差伪距残差 Fig. 4 Double-differenced bias of pseudorange |
由图 3和图 4可以看出, 修正之后的双差观测量残差均为白噪声, 由此, 频间偏差造成的系统偏差得以消除。
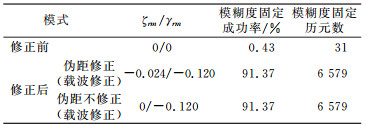
将得到的修正值应用于短基线模糊度解算。为进一步研究伪距频间偏差对模糊度解算的影响, 分别就修正前(载波、伪距均不修正)、伪距修正(载波)和伪距不修正(载波修正)3种模式进行实验分析比对, 对模糊度解算结果进行统计, 得到表 1和表 2。
|
|
表 1 模糊度固定结果 Tab. 1 AR performance |
|
|
表 2 模糊度固定结果 Tab. 2 AR performance |
可以看到, 2组数据修正前仅有35和31个历元得到固定解, 成功率极低, 分别为0.49%和0.43%;对载波相位观测量的频间偏差进行修正之后, 模糊度固定成功率得到极大提升, 分别达到99.93%和91.37%, 证明了对这部分偏差进行修正的必要性以及本文提出的校正方法的正确性。此外, 对比伪距修正与不修正2种解算策略, 模糊度固定效果是一样的, 这是由于非差伪距观测量的噪声为dm级, 而ζrm=-0.120 m, 二者属同一个量级, 因此该部分偏差修正值被观测噪声湮没, 这也表明了伪距观测量在RTK定位中的作用要远低于载波相位观测量。
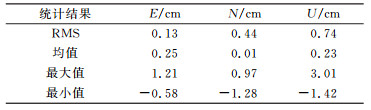
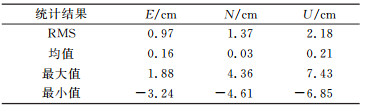
采用事后相对定位结果作为比对的真值, 对所有得到固定解的历元进行定位精度统计, 得到图 5、图 6、表 3、表 4。

|
图 5 定位偏差时序变化(11 m) Fig. 5 Time sequence of positioning error(11 m) |
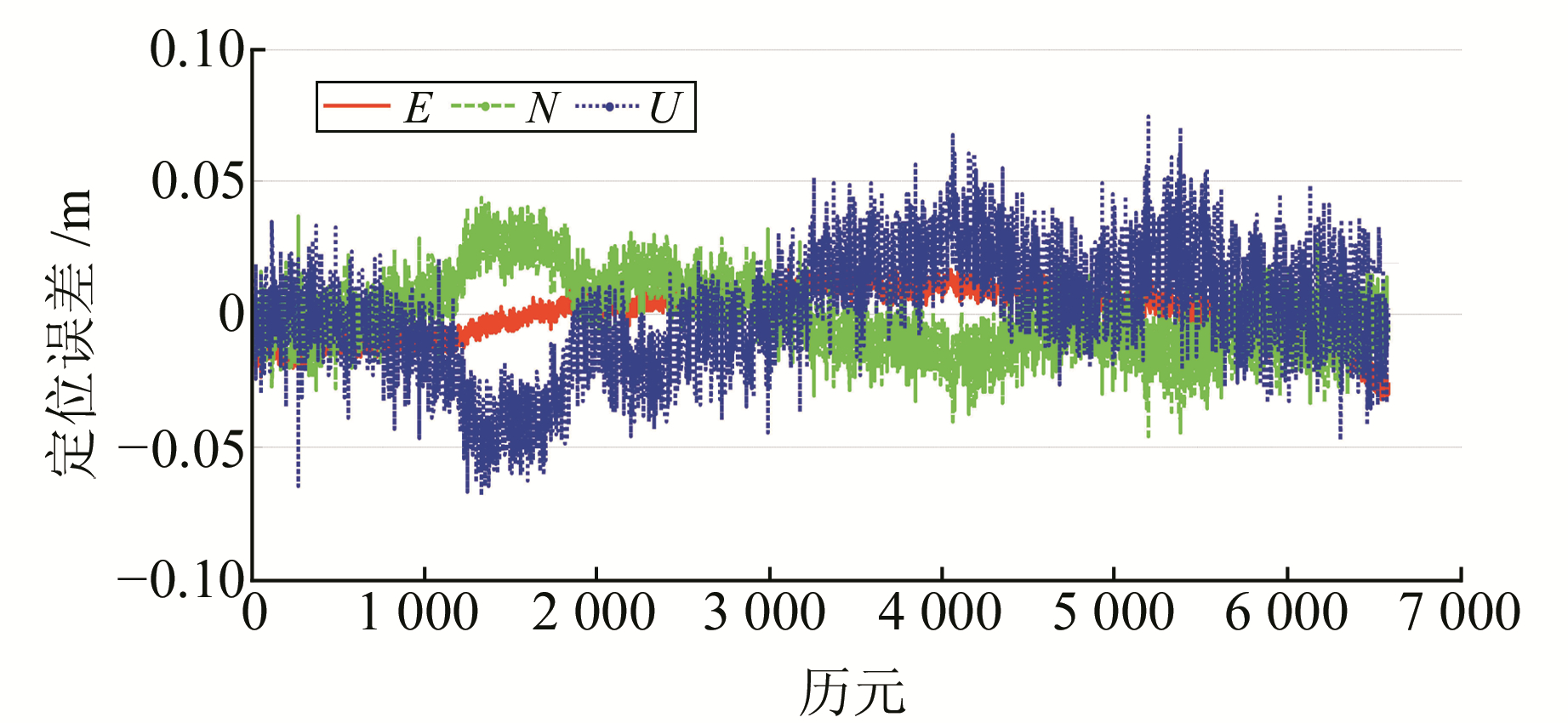
|
图 6 定位偏差时序变化(8 km) Fig. 6 Time sequence of positioning error(8 km) |
|
|
表 3 定位精度统计(11 m) Tab. 3 Statistical results of RTK positioning error(11 m) |
|
|
表 4 定位精度统计(8 km) Tab. 4 Statistical results of RTK positioning error(8 km) |
图 5中, E、N、U三个方向上的定位偏差都保持在2 cm以内。由表 3看出, 3个方向上的定位精度RMS分别为0.13 cm、0.44 cm和0.74 cm。图 6中, 基线长度增加到8 km, 3个方向上的定位偏差增大。由表 4看出, E、N、U方向上的定位RMS依次为0.97 cm、1.37 cm、2.18 cm。因此, 本文提出的修正方法是可行的。
4 结语采用不同的接收机对进行GLONASS/BDS联合RTK定位时, 需要对GLONASS观测量的频间偏差进行修正。本文分别就载波相位观测量和伪距观测量频间偏差的修正方法进行研究, 并采用短基线数据对所提修正方法的可行性进行验证。结果表明, 该方法可明显提高模糊度固定的成功率, 有效保证RTK解算结果的可靠性。文中采用零基线校正的方式对GLONASS接收机频间偏差进行修正, 然而在某些大规模CORS网中, 接收机类型繁多, 采用零基线方法显得较为繁琐, 并且一旦修正参数设置错误, 会造成严重后果, 今后将对这一问题进行研究。
| [1] |
Bernbard H W, Herbert L, Elmar W. GNSS-Global Navigation Satellite Systems:GPS, GIONASS, Galileo and More[M]. Berlin: Springer, 2008
(  0) 0) |
| [2] |
Al-Shaery A, Zhang S, Rizos C. An Enhanced Calibration Method of GLONASS Inter-Channel Bias for GNSS RTK[J]. GPS Solut, 2013, 17(2): 165-173 DOI:10.1007/s10291-012-0269-5
(  0) 0) |
| [3] |
Wanninger L. Carrier-Phase Inter-Frequency Biases of GLONASS Receivers[J]. J Geod, 2012, 86(2): 139-148 DOI:10.1007/s00190-011-0502-y
(  0) 0) |
| [4] |
李鹤峰, 党亚民, 秘金钟, 等. BDS与GPS、GLONASS多模融合导航定位时空统一[J]. 大地测量与地球动力学, 2013, 33(4): 73-78 (Li Hefeng, Dang Yamin, Bei Jinzhong, et al. Research on Spatio Tempora Unification of BDS/GPS/GLONASS Multi-Mode Fusion Navigation and Positioning[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 73-78)
(  0) 0) |
| [5] |
高星伟, 过静珺. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743-748 (Gao Xingwei, Guo Jingjun. Fushion Positioning of Compass/GPS Based on Spatio Temproal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743-748)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37