2. 解放军63798部队, 西昌市, 615000
GNSS整周模糊度解算是利用载波相位观测值进行cm级至mm级高精度定位的核心内容, 包括模糊度估计与模糊度确认2个部分[1]。其中, 模糊度估计分为2步:1)解算出模糊度的浮点解及其精度信息; 2)采用一定的搜索算法, 将浮点模糊度固定为整数[2]。
近几年, 国内外学者对GPS PPP模糊度固定进行了大量研究[3-9], 固定解PPP相较于浮点解PPP在定位性能上的提升作用得到广泛认可。然而, 模糊度固定的成功与否在一定程度上依赖于浮点模糊度的精度, 而PPP不可避免地存在收敛问题, 在动态模式下, 更是需要数十min才可以收敛[10]。若能在较短的时间内获得足够精度的浮点模糊度, 将有助于加速模糊度的固定, 提高模糊度固定的成功率。文献[11-15]对多GNSS组合PPP的研究表明, 在动态PPP中, 进行多系统组合可以有效缩短收敛时间并改善定位精度。这也反映了多GNSS组合PPP在较短时间内获得高精度浮点模糊度的特性, 但目前大部分多GNSS组合PPP仍采用浮点解, 未能充分利用这一特性。文献[16-17]进行GLONASS辅助GPS PPP模糊度固定的研究表明, 静态PPP中, 加入GLONASS后并没有明显缩短GPS模糊度首次固定时间; 但是在动态PPP中, 有效缩短了首次固定时间, 但未进行精度评估。也有研究表明, BDS/GPS/GLONASS三者组合PPP的收敛时间较BDS/GPS和GPS/GLONASS进一步减少且定位精度更高[14]。因此, 研究基于BDS/GPS/GLONASS融合的GPS PPP的模糊度固定方法以及该方法的定位性能很有必要。
本文首先阐述了整数相位钟法解算PPP模糊度的理论模型, 实现了GPS PPP模糊度的固定。在此基础上, 推导了基于整数相位钟法的BDS/GPS/GLONASS组合PPP模型, 利用多GNSS融合的方法, 加速浮点解的收敛, 从而在更短的时间内获得高精度的浮点解模糊度, 进而实现GPS PPP模糊度固定。最后, 通过6个MGEX测站的数据进行PPP动态实验, 在定位精度、首次固定时间、模糊度固定率等方面进行统计分析, 对本文所提出的方法进行验证。
1 BDS/GPS/GLONASS组合PPP模型与模糊度固定方法 1.1 整数相位钟法的模糊度固定策略整数相位钟法固定模糊度的重要思想是将伪距钟差和载波相位钟差进行区分[3, 6, 9]。基于该思想, GPS消电离层组合观测方程可表示为:
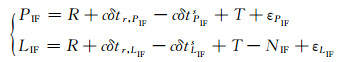
|
(1) |
式中, PIF、LIF分别为消电离层组合伪距和载波相位观测值, R为卫星至测站的几何距离, c为光速, δtr, PIF、δtsPIF为伪距接收机钟差和伪距卫星钟差, δtr, LIF、δtsLIF为载波相位接收机钟差和载波相位卫星钟差, NIF为消电离层组合模糊度, T为对流层湿延迟, εPIF、εLIF分别为伪距和载波相位的测量噪声及误差残余。其中,
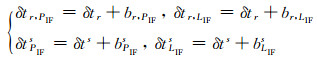
|
(2) |
式中, br, PIF、bsPIF分别为伪距观测值接收机端和卫星端对应的时间偏差项, br, LIF、bsLIF分别为载波相位观测值接收机端和卫星端偏差对应的时间偏差项。在传统的浮点解PPP中, IGS精密钟差产品中包含了伪距观测值卫星端对应的时间偏差项bsPIF, 即δtsPIF。而在参数解算时, 实际估计的接收机钟差则包含了伪距观测值接收机端对应的时间偏差项, 即δtr, PIF。
由此可以看到, 在传统浮点解PPP中, 本文实际求解的模糊度为:
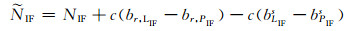
|
(3) |
其受到了c(br, LIF-br, PIF)-c(bsLIF-bsPIF)的污染, 因此不能准确固定为整数。而从式(1)中可以看出, 采用区分伪距钟差和载波相位钟差的方法, 可以使c(br, LIF-br, PIF)-c(bsLIF-bsPIF)从消电离层模糊度中剥离出来。
目前, CNES公布了基于载波相位卫星钟差δtsLIF的精密钟差产品, 引入CNES精密卫星钟差后, 即可消除偏差项cδtsLIF, 并能削弱cδtsPIF对伪距观测量的影响。在此基础上进行星间单差处理, 消除偏差项cδtr, LIF和δtr, PIF的影响:
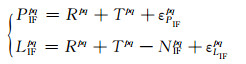
|
(4) |
式中, p代表基准星, q代表流动星。NIFpq可分解为:
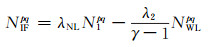
|
(5) |
式中, λNL为窄巷波长, 约为10.7 cm, N1pq为单差窄巷模糊度, λ2为载波L2的波长, γ=f12/f22, f1、f2分别为载波L1、L2的频率, NWLpq为单差宽巷模糊度。
在获得单差消电离层模糊度浮点解后, 利用MW组合观测值和CNES提供的宽巷偏差产品求得单差宽巷模糊度固定解; 再利用单差消电离层模糊度浮点解和单差宽巷模糊度固定解求得单差窄巷模糊度浮点解, 利用单差消电离层模糊度协方差阵求得单差窄巷模糊度协方差阵; 然后通过部分模糊度固定方法求得单差窄巷模糊度固定解[18-19]; 最后根据式(3), 利用固定的单差窄巷模糊度和单差宽巷模糊度求得单差消电离层模糊度固定解[9]。
1.2 BDS/GPS/GLONASS组合PPP模型在进行BDS/GPS/GLONASS组合PPP时, 对各系统分别引入参考星, 则相应的单差观测方程为:
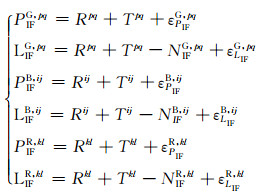
|
(6) |
式中, 上标G代表GPS卫星, p代表GPS基准星, q代表GPS流动星, B代表BDS卫星, i代表BDS基准星, j代表BDS流动星, R代表GLONASS卫星, k代表GLONASS基准星, l代表GLONASS流动星。
利用式(6)进行组合PPP解算, 从而获得单差消电离层模糊度浮点解, 然后通过前文所述的模糊度固定方法进行固定。需要指出的是, 目前仅CNES公布了用于GPS PPP模糊度固定的相应产品(整数相位钟产品和宽巷模糊度偏差产品), 因此只能进行GPS模糊度固定, 对于BDS和GLONASS, 始终保持浮点模糊度。
2 算例与结果分析 2.1 实验数据与方案为验证本文所提出的模糊度估计方法, 选取DJIG、DYNG、GMSD、NNOR、ONS1、REUN共6个MGEX跟踪站2015年年积日第203天02:00~22:00的观测数据进行动态定位实验。其中, DJIG位于吉布提, DYNG位于希腊, GMSD位于日本, NNOR位于澳大利亚, ONS1位于挪威, REUN位于南非。每个测站均可接收BDS、GPS、GLONASS3种卫星信号, 采样间隔为30 s。对于精密产品, BDS、GLONASS采用GFZ分析中心发布的30 s精密钟差和5 min的精密星历; GPS采用CNES分析中心提供的30 s精密钟差和15 min的精密星历。
将每份观测数据以4 h划分为1个观测时段, 每个测站5个观测时段, 6个测站共计30个观测时段。对于每个观测时段的数据, 分别采用4种模式的解算方案(GPS PPP浮点解、GPS PPP固定解、BDS/GPS/GLONASS PPP浮点解、BDS/GPS/GLONASS PPP固定解)进行计算。
卫星截止高度角设置为10°, 利用消电离层组合消除电离层一阶项的影响; 采用Sasstamonion模型改正对流层干分量, 将对流层湿分量作为未知参数进行估计; 对于接收机钟差, 采用星间单差法予以消除; 对于相对论相应、固体潮汐、PCO、PCV以及相位缠绕效应, 进行相应的模型改正(BDS只进行粗略的PCO改正), 参数估计方法采用扩展卡尔曼滤波。
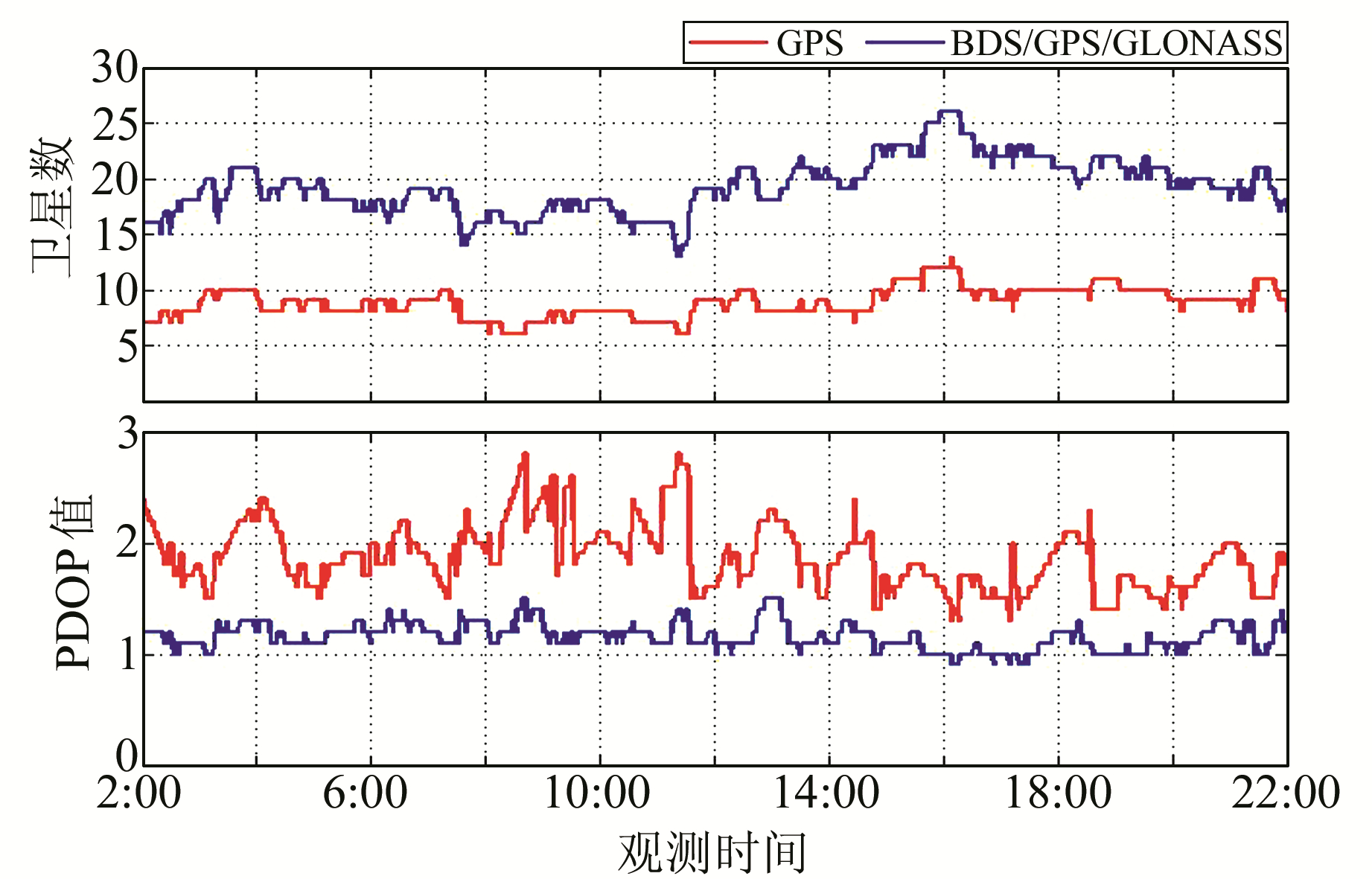
2.2 实验结果分析 2.2.1 可见卫星数与PDOP值以ONS1站为例, 给出该站在观测时段内GPS系统、BDS/GPS/GLONASS组合系统的可视卫星数(NAST)和PDOP, 如图 1所示。可以看出, 在观测时段内, GPS单系统的可见卫星数为6~13颗, 而BDS/GPS/GLONASS组合系统的可见卫星数为13~26颗, 几乎是GPS单系统的2倍; 大部分观测时间内, GPS的PDOP值在1.5~3.0, 而组合系统的PDOP值在1.0~1.5, 几乎是单系统的1/2。这也反映了多系统组合相较于GPS单系统, 具有更好的空间几何构型。需要指出的是, ONS1站位于挪威, 可观测到的BDS卫星数相对较少, 若是在亚太地区的测站(GMSD和NNOR), 则可观测到的BDS卫星更多, BDS/GPS/GLONASS组合系统相对于GPS单系统在可见卫星数方面的优势将更为明显。
|
图 1 ONS1站可见卫星数与PDOP值 Fig. 1 Visible satellite numbers and PDOP values at station ONS1 |
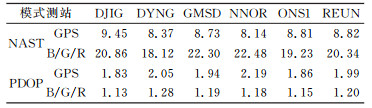
如表 1所示, 位于亚太地区的测站GMSD和NNOR平均可见卫星数均在22颗以上, 而其他测站的平均可见卫星数则在18~21颗。总体上看, GPS单系统的平均可见卫星数在8~10颗, 而3个系统组合的平均可见卫星数大幅增加, 约为单系统的2~3倍; GPS单系统的PDOP平均值在1.8~2.2, 而3个系统组合的PDOP平均值则在1.1~1.3, 明显减小, 充分证明了多系统组合在空间几何构型上的优越性。
|
|
表 1 各站平均可见卫星数与PDOP平均值 Tab. 1 The average of visible satellite numbers and PDOP values per station |
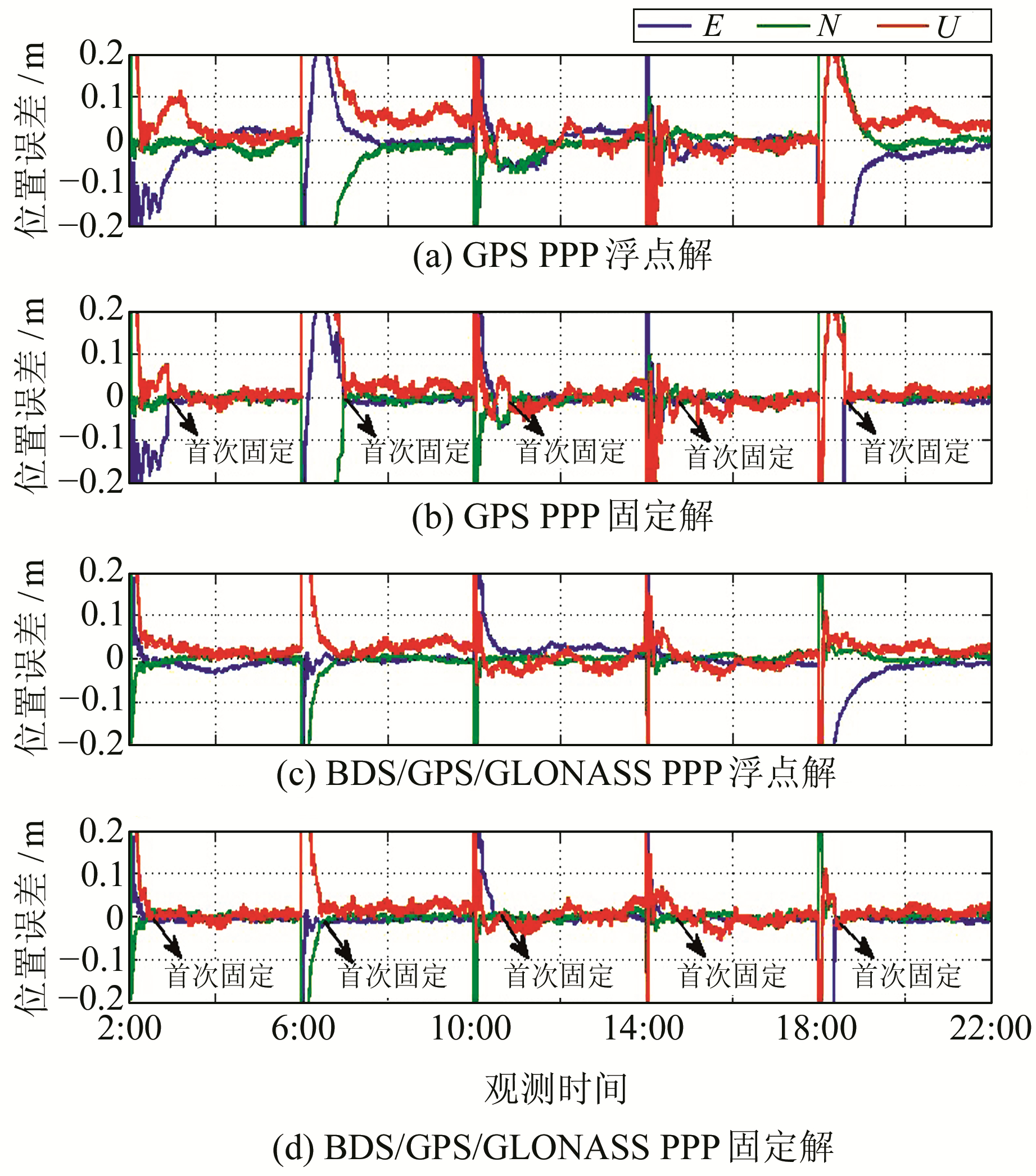
以CNES发布的单天解作为参考真值, 将解算结果与参考真值作差, 获得E、N、U 3个方向的坐标偏差。同样以ONS1站为例, 给出4种PPP解算方案的位置偏差图(图 2)。从图中不难看出, BDS/GPS/GLONASS组合加速了浮点解的收敛, 并且使收敛后的浮点解位置误差更小。而一旦实现模糊度固定, 无论是GPS单系统, 还是BDS/GPS/GLONASS组合系统, 其位置误差会迅速减小, 并且模糊度固定后的定位结果更为稳定。
|
图 2 ONS1站4种动态PPP位置偏差 Fig. 2 Four kinds of kinematic PPP position bias at station ONS1 |
选取每个观测时段最后2 h的定位结果进行统计分析。图 3给出各测站5个观测时段位置偏差的平均RMS, 从左至右依次为DJIG、DYNG、GMSD、NNOR、ONS1和REUN。综合来看, BDS/GPS/GLONASS组合PPP的位置精度要优于单GPS的位置精度, 固定解的位置精度要优于浮点解。
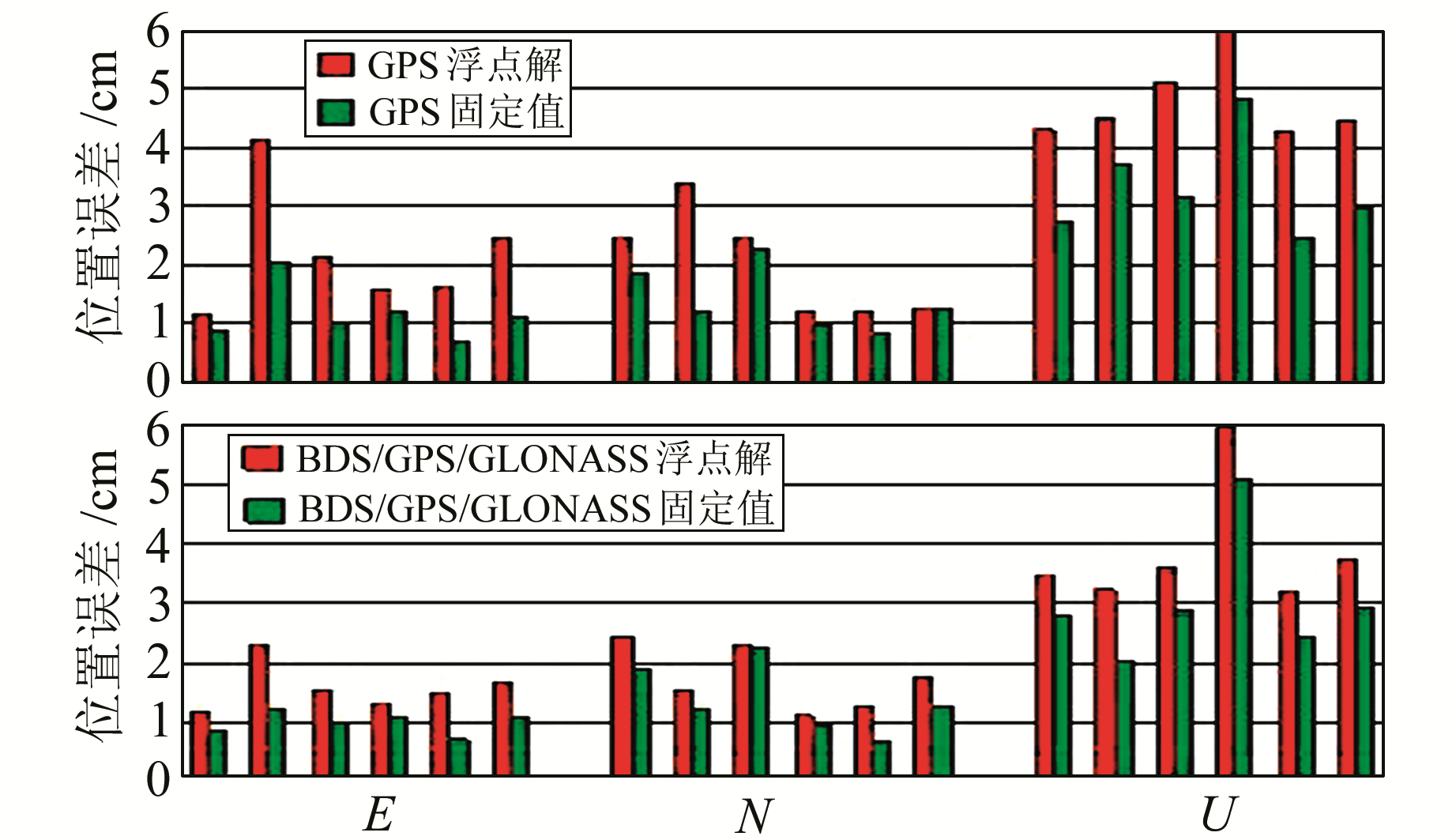
|
图 3 各测站4种动态PPP位置偏差统计 Fig. 3 Statistics of positioning bias of 4 kinds of kinematic PPP per station |
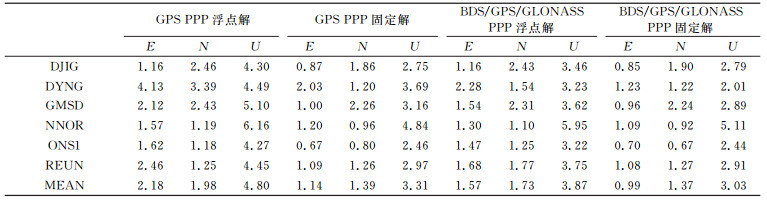
表 2(单位cm)给出了位置误差的RMS具体统计信息。其平均统计结果显示, GPS PPP浮点解E、N、U方向上的RMS分别为2.18 cm、1.98 cm、4.80 cm, GPS PPP固定解则为1.14 cm、1.39 cm、3.31 cm, 分别减少了47.7%、29.8%、31.0%;对于BDS/GPS/GLONASS PPP固定解, 其E、N、U方向上的RMS分别为0.99 cm、1.37 cm、3.03 cm, 相较于GPS PPP浮点解分别减少了54.6%、30.8%、36.9%, 相较于GPS PPP固定解也有所提升。4种解算方案中, 基于BDS/GPS/GLONASS融合的GPS固定解PPP定位精度最高。
|
|
表 2 各站动态PPP定位偏差RMS统计 Tab. 2 Statistics of RMS position bias of kinematic PPP per station |
从图 2还可以发现, 当进行3个系统组合时, 模糊度的首次固定时间有所减少, 可获得固定解的历元有所增加。为进一步分析多系统组合对模糊度固定的影响, 进行以下统计。
首先是模糊度首次固定时间。图 4给出6个测站30个观测时段的首次固定时间(TTFF)。可以看出, 当进行BDS/GPS/GLONASS组合时, GPS模糊度的首次固定时间均有不同程度的减少。此外, 各测段之间GPS单系统的首次固定时间变化较大, 由20~100 min不等; 而BDS/GPS/GLONASS组合下的GPS模糊度首次固定时间较为稳定, 变化范围在20~40 min。
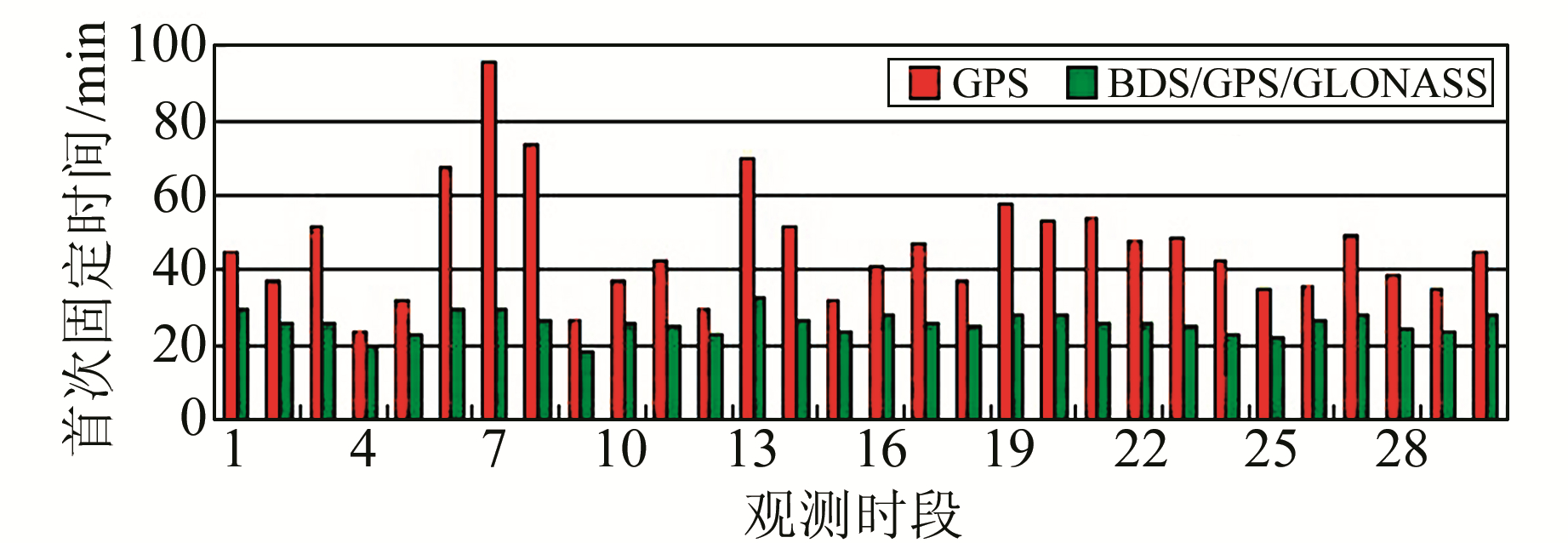
|
图 4 30个观测时段的首次固定时间 Fig. 4 TTFF of 30 sessions |
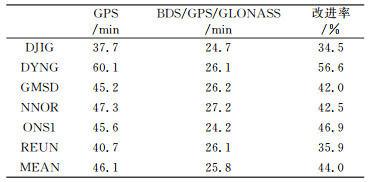
表 3给出了各测站模糊度首次固定时间的具体统计信息。结果显示, GPS PPP模糊度首次固定时间平均为46.1 min, 而BDS/GPS/GLONASS组合下的GPS PPP模糊度首次固定时间平均仅为25.8 min, 相比于GPS单系统减少了44.0%。
|
|
表 3 各站平均首次固定时间 Tab. 3 The average of TTFF per station |
本文还对PPP模糊度固定率进行了统计。模糊度固定率定义为:
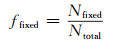
|
(6) |
式中, Nfixed为可进行固定解的历元数, Ntotal为观测时段内总的历元数, ffixed为Nfixed和Ntotal的比值。各测站模糊度固定率的具体统计信息见表 4。
|
|
表 4 各站平均模糊度固定率 Tab. 4 The average ambiguity fixing rate per station |
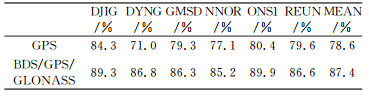
从表 4可以看出, 在观测时长为4 h的情况下, GPS单系统的平均模糊度固定率为78.6%, 而BDS/GPS/GLONASS组合PPP模糊度固定率为87.4%, 提升了近9个百分点。这主要是由于:1) BDS/GPS/GLONASS组合PPP减少了模糊度首次固定时间, 致使GPS单系统模糊度首次固定之前的部分历元的模糊度得以固定; 2)单GPS模式下, 模糊度首次固定之后的部分历元模糊度固定失败, 而组合PPP相对于GPS单系统PPP, 可以获得更高精度的浮点模糊度, 提高了模糊度正确固定的可能性, 致使这部分历元实现了模糊度固定。
3 结语本文探讨了PPP模糊度估计方法, 实现了GPS PPP模糊度固定, 并在此基础上, 研究了基于多GNSS融合的PPP模糊度固定方法。利用MGEX站的实测数据进行动态PPP解算的实验结果表明:
1) GPS PPP浮点解E、N、U方向上的RMS分别为2.18 cm、1.98 cm、4.80 cm, GPS PPP固定解则为1.14 cm、1.39 cm、3.31 cm, 分别减少了47.7%、29.8%、31.0%;而BDS/GPS/GLONASS组合下的GPS PPP固定解定位精度更高, E、N、U方向上的RMS分别为0.99 cm、1.37 cm、3.03 cm, 相较于GPS PPP浮点解分别减少了54.6%、30.8%、36.9%。
2) GPS固定解PPP平均模糊度首次固定时间为46.1 min, 而基于BDS/GPS/GLONASS融合的固定解PPP首次固定时间仅为25.8 min, 减少了44.0%。
3) 在观测时长为4 h的情况下, GPS PPP的模糊度固定率为78.6%, 而BDS/GPS/GLONASS组合PPP的模糊度固定率为87.4%, 提升了近9个百分点。
综上所述, 相较于单GPS固定解PPP, 基于BDS/GPS/GLONASS融合的GPS固定解PPP减少了模糊度首次固定时间, 提高了固定率, 并改善了定位精度, 具有更为优越的定位性能。
| [1] |
Kleusberg A, Teunissen P J G. GPS for Geodesy[M]. Berlin: Springer, 1996
(  0) 0) |
| [2] |
刘经南, 邓辰龙, 唐卫明, 等. GNSS整周模糊度确认理论方法研究进展[J]. 武汉大学学报:信息科学版, 2014, 39(9): 1009-1016 (Liu Jingnan, Deng Chenlong, Tang Weiming, et al. Review of GNSS Ambiguity Validation Theory[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1009-1016)
(  0) 0) |
| [3] |
Laurichesse D, Mercier F, Berthias J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Journal of the Institute of Navigation, 2009, 56(2): 135-149 DOI:10.1002/navi.2009.56.issue-2
(  0) 0) |
| [4] |
Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning with Daily Observation[J]. Journal of Geodesy, 2008, 82(7): 389-339 DOI:10.1007/s00190-007-0187-4
(  0) 0) |
| [5] |
Collins P, Bisnath S, Lahaye F, et al. Undifferenced GPS Ambiguity Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123-135 DOI:10.1002/navi.2010.57.issue-2
(  0) 0) |
| [6] |
Loyer S, Perosanz F, Mercier F, et al. Zero-Difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012, 86(11): 991-1003 DOI:10.1007/s00190-012-0559-2
(  0) 0) |
| [7] |
Shi J B.Precise Point Positioning Inter Ambiguity Resolution with Decoupled Clocks[D]. Calgary: University of Calgary, 2012
(  0) 0) |
| [8] |
Zhang X H, Li P, Guo F. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Adv Space Res, 2013, 51(8): 153-161
(  0) 0) |
| [9] |
刘帅, 孙付平, 郝万亮, 等. 整数相位钟法精密单点定位模糊度固定模型及效果分析[J]. 测绘学报, 2014, 43(12): 1230-1237 (Liu Shuai, Sun Fuping, Hao Wanliang. Modeling and Effects Analysis of PPP Ambiguity Fixing Based on Inter Phase Clock Method[J]. Acta Geod Cartogr Sin, 2014, 43(12): 1230-1237)
(  0) 0) |
| [10] |
Geng J, Teferle F N, Meng X, et al. Towards PPP-RTK: Ambiguity Resolution in Real-Time Precise Point Positioning[J]. Adv Space Res, 2011, 47(10): 1664-1673 DOI:10.1016/j.asr.2010.03.030
(  0) 0) |
| [11] |
Cai C S, Gao Y. Performance Analysis of Precise Point Positioning Based on Combined GPS and GLONASS[C]. The ION GNSS 20th International Technical Meeting of the Satellite Division, Shanghai, 2007
(  0) 0) |
| [12] |
Anquela A B, Martin A, Berne J L, et al. GPS and GLONASS Static and Kinematic PPP Results[J]. Journal of Surveying Engineering, 2013, 139(1): 47-58 DOI:10.1061/(ASCE)SU.1943-5428.0000091
(  0) 0) |
| [13] |
Li M, Qu L Z. Precise Point Positioning with the Beidou Navigation Satellite System[J]. Sensor, 2014, 14(1): 927-943 DOI:10.3390/s140100927
(  0) 0) |
| [14] |
Li P, Zhang X H.Modeling and Performance Analysis of GPS/GLONASS/BDS Precise Point Positioning[C].China Satellite Navigation Conference, Nanjing, 2014
(  0) 0) |
| [15] |
Odijk D, Zhang B C, Teunissen P J G.Multi-GNSS PPP and PPP-RTK: Some GPS+BDS Results in Australia[C].China Satellite Navigation Conference, Xi'an, 2015
(  0) 0) |
| [16] |
Jokinen A, Feng S J, Schuster W, et al. GLONASS Aided GPS Ambiguity Fixed Precise Point Positioning[J]. The Journal of Navigation, 2013, 66(3): 399-416 DOI:10.1017/S0373463313000052
(  0) 0) |
| [17] |
Li P, Zhang X H. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471 DOI:10.1007/s10291-013-0345-5
(  0) 0) |
| [18] |
Shi J, Gao Y. A Fast Integer Ambiguity Resolution Method for PPP[C]. ION GNSS, Nashville, 2012
(  0) 0) |
| [19] |
Li P, Zhang X H. Precise Point Positioning with Partial Ambiguity Fixing[J]. Sensor, 2015, 15(6): 13627-13643 DOI:10.3390/s150613627
(  0) 0) |
2. PLA 63798 Troops, Xichang 615000, China
 2017, Vol. 37
2017, Vol. 37