2. 北斗导航应用技术河南省协同创新中心, 郑州市科学大道62号, 450001;
3. 西安卫星测控中心, 西安市咸宁东路28号, 710043;
4. 信息工程大学地理空间信息学院, 郑州市科学大道62号, 450001
PPP时频传递技术由于采用的载波相位观测值具有精度高、噪声小的特点, 授时结果的不确定度可达0.2 ns, 1 d的频率稳定度可以达到10-15甚至更好[1]。但文献[2-3]在采用PPP技术进行单站授时解算时, 得到的结果与IGS结果存在明显的系统性偏差, 且不同测站呈现出的系统性偏差并不相同。为提高PPP授时的绝对精度, 有必要对引起单站授时结果系统性偏差的因素进行分析。本文从授时基本观测方程入手, 对引起系统性偏差产生的原因进行研究, 并以GPS系统为例, 通过具体实验进行分析。
1 PPP授时模型对于双频接收机, PPP授时算法一般采用载波相位和伪距消电离层组合观测量, 观测方程为:

|
(1) |
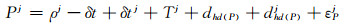
|
(2) |
式中, j为卫星号, Φ和P分别为载波相位和伪距消电离层组合观测量, ρ为接收机到卫星的几何距离, δt、δtj为接收机和卫星钟差, N为消电离层组合模糊度, T为对流层延迟, dhd(Φ)、dhd(P)为接收机载波相位硬件延迟和码硬件延迟, dhd(Φ)j、dhd(P)j为卫星载波相位硬件延迟和码硬件延迟, εΦj、εPj为未模型化的误差影响。
2 系统性偏差因素分析 2.1 卫星钟差对授时结果的影响分析通常IGS发布的事后卫星精密钟差是相对于基准钟的相对钟差, 基准钟一般都会与标准时间存在时间偏差, 这就使得各颗卫星钟差中都增加了同样大小的时间偏差, 由基准钟引起的系统性偏差对同一历元所有卫星均相同[4-5]。设某一历元由基准钟引起的卫星钟系统性偏差为t0, 第j颗卫星绝对钟差为δtj, 则相对钟差为δtj-t0。当卫星钟差系统性偏差小于2.5×10-7 s时, 对卫星位置计算造成的影响可以忽略, 其主要是引起几何距离计算误差[5]。利用含有系统性偏差的卫星钟差进行解算, 观测方程和变为:

|
(3) |

|
(4) |
由于系统偏差对所有卫星相同, 可以将系统性偏差和接收机钟差合并:

|
(5) |

|
(6) |
对比原始观测方程和可以看出, 方程和除了待估接收机钟差参数含义有所变化外, 其他未知参数及系数矩阵完全相同。也就是说, 解算过程中卫星钟差系统性偏差会完全被接收机钟差吸收, 对授时结果造成系统性影响。这一影响与测站无关, 且对所有测站均相同。
为了验证上述分析结果, 采用2015-01-14 NRC1和BRUX两个配有外接高稳定度频率基准的IGS站观测数据进行实验分析, 数据采样间隔30 s。由于IGS和CODE分析中心在解算卫星钟差时选择的基准钟不同(IGS时间基准为IGST, CODE时间基准为ONSA), 导致2个分析中心卫星钟差间存在系统性偏差。将2个分析中心同一卫星钟差作差, 得到由基准钟引起的系统性偏差结果, 理论上各颗卫星的系统性偏差均相同。分别采用IGS和CODE发布的事后卫星精密钟差进行PPP授时实验, 将2种方案计算得到的接收机钟差结果作差, 得到由卫星钟差产品引起的授时结果的系统性偏差。图 1给出了NRC1和BRUX测站由卫星钟差产品引起的单站授时系统性偏差结果, 以及01、10、20和25四颗卫星由2个分析中心产品互差计算的系统性偏差结果。

|
图 1 卫星和测站钟差系统性偏差 Fig. 1 Results of satellite and station clock systematic bias |
实验结果表明, 利用不同卫星钟差产品解算得到的接收机钟差间存在系统性偏差, 这一系统性偏差与各卫星的系统性偏差变化趋势十分一致, 且这一系统性偏差是随时间变化的, 其包含了各自基准钟随时间的变化。理论上各测站授时结果的系统性偏差和各颗卫星的系统性偏差应该是完全一致的, 但图上呈现出的系统偏差稍有不同, 这主要是由于解算过程中数据处理策略的差异, 以及各颗卫星观测数据质量的差异造成的, 但相互之间差别不大, 互差精度平均在0.2 ns以内。不同分析中心提供的卫星精密钟差产品时间基准不同, 这会对授时结果造成系统性偏差, 且对所有测站影响相同, 在进行单站授时时必须要考虑卫星钟差产品的影响。考虑到站间时间传递是将2个测站的授时结果相减得到, 只要2个测站使用同一分析中心的卫星精密钟差产品, 保证站间授时结果的一致性, 在进行站间时间传递时就可以有效消除卫星钟差产品引起的系统性偏差。
2.2 硬件延迟对授时结果的影响分析PPP授时使用精密星历和精密钟差产品后, 卫星轨道误差和钟差误差的影响可以忽略, 此时影响授时精度的主要误差是信号传播路径误差和设备时延误差。信号传播路径误差可以通过观测量组合和模型改正的方式进行消除, 而设备时延误差主要通过专用设备进行标定或采用相对校准的方式测量标校。设备时延主要包括卫星端硬件延迟和接收机端硬件延迟[6-8], 目前针对接收机DCB参数对授时结果影响的研究较少。
在利用方程和进行解算时, 钟差和硬件延迟不可分离。卫星硬件延迟对授时结果的影响主要体现在对卫星钟差的改正上, 不同的卫星硬件延迟不同, 应当对其进行改正。接收机硬件延迟只与接收机有关, 对所有卫星观测量的影响相同, 解算过程中被吸收到接收机钟差参数中, 对授时结果造成系统性偏差影响。伪距观测方程变为:

|
(7) |
观察方程可知, 接收机钟差参数和模糊度参数是一一相关、无法分离的, 钟差误差可以完全被模糊度误差所补偿, 同时载波相位的硬件延迟也会被模糊度参数吸收, 这时相应的新模糊度参数NNj将包含硬件延迟:

|
(8) |
此时载波相位方程变为:
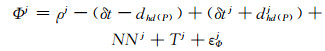
|
(9) |
在定位过程中接收机码硬件延迟完全被接收机钟差参数吸收, 不会影响定位结果, 通常不需要进行改正。但在授时过程中, 接收机码硬件延迟会对授时结果造成系统性偏差。为有效分离接收机钟差和码硬件延迟, 提高授时的绝对精度, 必须对接收机码硬件延迟进行改正。
目前IGS各分析中心提供的精密钟差是以双频P码消电离层解算得到的, 已经包含了P1和P2码观测量的硬件延迟[8-9]。为保证观测量与P1和P2观测量的一致性, 在利用P1和C1观测量进行解算时必须对P1和C1观测量的码硬件延迟偏差DCB进行改正。采用消电离层进行授时解算时, 只需要在组合观测量上加1个与C1和P1码硬件延迟偏差BP1-C1相关的改正。不同类型的接收机加的改正量不同, C1/P2型接收机为2.546BP1-C1, C1/X2型接收机为BP1-C1。对于P1/P2型接收机, 若采用P1和P2观测量进行解算则不需要对硬件延迟进行改正[9-10]。接收机DCB短期内十分稳定, 可当作不变的常量, IGS每月发布1次各测站的接收机硬件延迟偏差[8]。
为了验证接收机码硬件延迟对授时结果的影响, 选取2015-01-04 NRC1和BRUX站观测数据和CODE发布的事后卫星精密星历和钟差产品进行静态实验分析, 数据采样间隔为30 s, 码观测量采用C1和P2观测量, 接收机DCB从IGS提供的P1C11501_RINEX.DCB文件中提取。分别用加接收机DCB改正和不加接收机DCB改正2种方法进行实验, 2种方法除对接收机DCB处理方式不同外, 其他处理策略完全一致。图 2和图 3分别给出了NRC1和BRUX站采用2种方法得到的单站授时结果与CODE事后精密钟差序列的对比。

|
图 2 2种方法结果与CODE真值序列对比(NRC1) Fig. 2 Difference of the results based on two methods from CODE real values(NRC1) |

|
图 3 2种方法结果与CODE真值序列对比(BRUX) Fig. 3 Difference of the results based on two methods from CODE real values(BRUX) |
由图 2和图 3可以看出, 2种方法计算得到的NRC1和BRUX站的授时结果与CODE事后结果变化趋势十分一致, 但加入DCB改正后的结果与CODE结果符合度更高, 未加接收机DCB改正的结果与CODE结果明显存在系统性偏差。
为更好地分析DCB对授时结果的影响, 直接将2种方法的授时结果作差, 可以完全消除对流层延迟、多路径、电离层高阶项改正等误差的影响, 所得授时结果误差中只含有接收机DCB的影响。图 4给出了NRC1和BRUX站2种方法互差时间序列。

|
图 4 测站钟差互差序列 Fig. 4 Difference of the results between two methods |
表 1(单位ns)给出了2个测站接收机C1和P1码硬件延迟偏差BP1-C1、解算时在伪距消电离层组合上加改正量2.546BP1-C1以及最终对授时结果造成的系统性偏差。
|
|
表 1 DCB及系统性偏差 Tab. 1 DCB and systematic bias |
由图 2、图 4及表 1可知, 2种方法解算得到的接收机钟差序列变化趋势十分一致, 即噪声水平基本相同, 但未加DCB改正的计算结果与加DCB改正的计算结果存在系统性偏差。这一系统性偏差较为稳定, 且不同测站的系统性偏差大小不同, BRUX站为-3.017 ns, NRC1站为-4.440 ns。
由表 1可知, 接收机DCB引起的授时结果系统性偏差的大小取决于接收机C1和P1码观测量的硬件延迟偏差。在授时过程中, BP1-C1乘以一定的放大倍数加在伪距消电离层组合观测量上, 对伪距组合观测量的改正量完全被接收机钟差参数吸收, 对接收机钟差造成同样大小的系统性偏差, 这也从侧面证明伪距决定授时结果的绝对精度。不同测站的接收机DCB不同, 对授时结果造成的影响也不相同, 因此在单站授时及站间时间传递时必须要对接收机硬件延迟偏差进行改正。
为了从频率稳定度角度进一步分析接收机DCB对授时结果造成的影响, 采用重叠Allan方差来计算接收机钟差的频率稳定度[11], 其公式为:
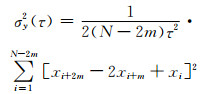
|
(10) |
式中, xi为历元i对应的钟差数据, τ=mτ0为取样时间, N为采样个数, m为钟差平滑因子, 一般取
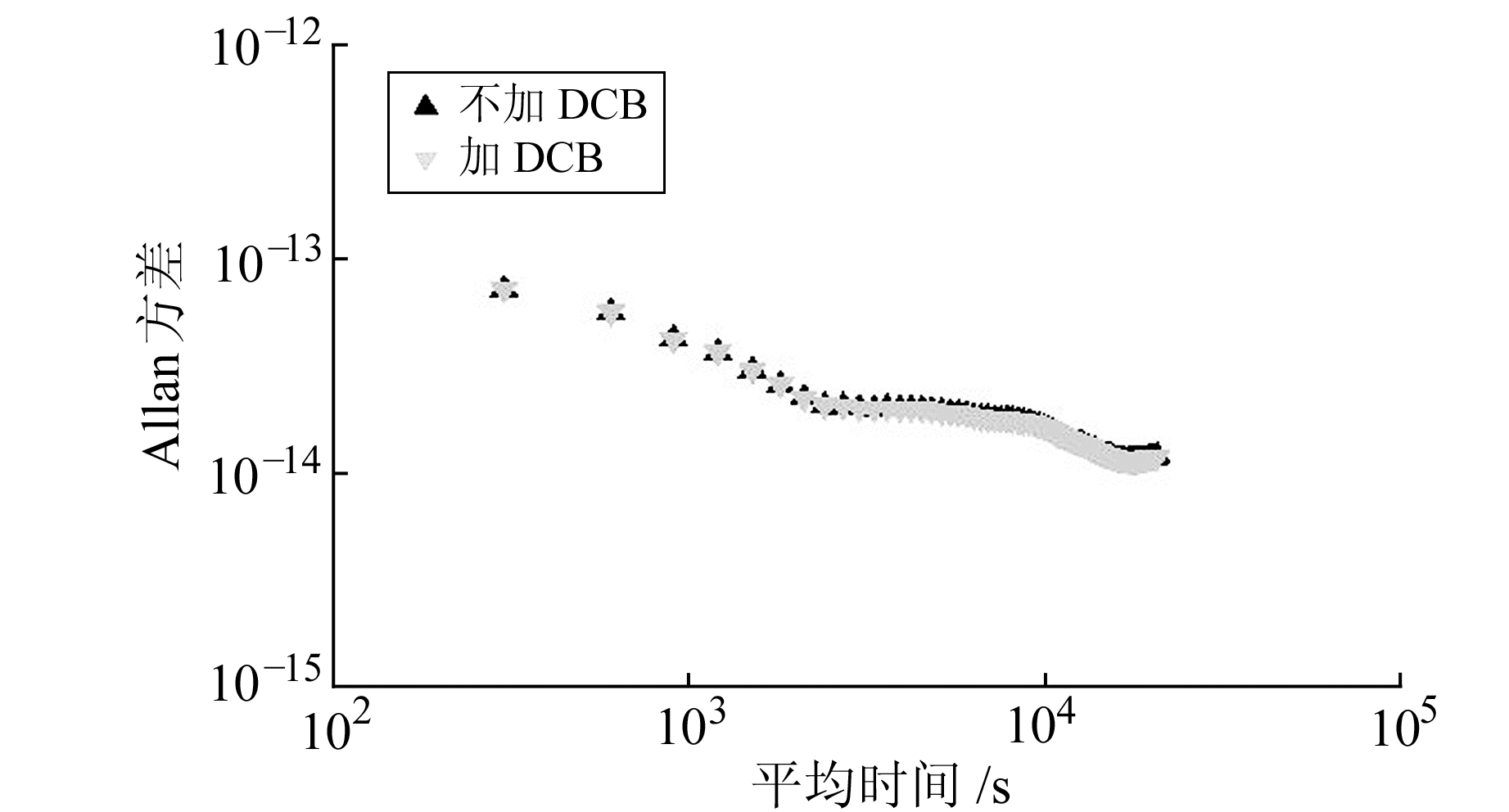
利用重叠Allan方差公式对2种方法得到的测站NRC1和BRUX钟差结果进行频率稳定度分析, 结果如图 5和图 6所示。
|
图 5 2种方法授时结果频率稳定性分析(NRC1) Fig. 5 Frequency stability of the two methods(NRC1) |

|
图 6 2种方法授时结果频率稳定性分析(BRUX) Fig. 6 Frequency stability of the two methods(BRUX) |
从图 5和图 6可以看出, 接收机DCB改正前后, 测站NRC1和BRUX的授时结果的频率稳定曲线几乎完全重叠, 即接收机DCB对授时结果的频率稳定度影响极小, 可以忽略不计, 因此在进行频率传递时无需考虑接收机DCB的影响。
3 结语卫星钟差产品会对授时结果造成系统性偏差影响, 这一系统性偏差是随时间变化的, 在进行单站授时必须要考虑卫星钟差产品的影响。卫星钟差产品对所有测站造成的影响相同, 只要各测站使用同一分析中心的卫星钟差产品, 保证各站授时结果的一致性, 在进行站间时间传递时就可以有效消除卫星钟差产品的影响。
接收机DCB对授时结果造成的影响表现为系统性的偏差, 这一系统性偏差较为稳定, 其大小取决于测站接收机硬件延迟偏差的大小。不同测站的接收机硬件延迟偏差不同, 对授时结果造成的系统性偏差影响也不相同。因此在单站授时及站间时间传递时, 必须顾及接收机硬件延迟的影响。接收机DCB不会影响授时结果的频率稳定度, 在进行频率传递时无需考虑接收机DCB的影响。
| [1] |
Yao J. Continuous GPS Carrier-Phase Time Transfer[D]. Boulder: University of Colorado at Boulder, 2014
(  0) 0) |
| [2] |
黄观文.GNSS星载原子钟质量评价及精密钟差算法研究[D].西安: 长安大学, 2012 (Huang Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang' an University, 2012) https://baike.baidu.com/item/GNSS%E6%98%9F%E8%BD%BD%E5%8E%9F%E5%AD%90%E9%92%9F%E8%B4%A8%E9%87%8F%E8%AF%84%E4%BC%B0%E5%8F%8A%E7%B2%BE%E5%AF%86%E9%92%9F%E5%B7%AE%E7%AE%97%E6%B3%95/22248081
(  0) 0) |
| [3] |
李红涛.基于GPS和GLONASS的单站授时及时差监测研究[D].西安: 长安大学, 2012 (Li Hongtao. Research on the Single Station Time Service and Time Offset Based on the GPS and GLONASS Data[D]. Xi'an: Chang' an University, 2012)
(  0) 0) |
| [4] |
楼益栋.导航卫星实时精密定轨与钟差确定[D].武汉: 武汉大学, 2008 (Lou Yidong. Research on Real-Time Precise GPS Orbit and Clock Offset Determination[D]. Wuhan: Wuhan University, 2008)
(  0) 0) |
| [5] |
于合理, 郝金明, 宋超, 等. 卫星钟系统偏差对精密单点定位精度的影响[J]. 测绘科学技术学报, 2013, 30(2): 136-139 (Yu Heli, Hao Jinming, Song Chao, et al. Impact of Satellite Clock Systematic Bias on Precise Point Positioning Accuracy[J]. Journal of Geomatics Science and Technology, 2013, 30(2): 136-139 DOI:10.3969/j.issn.1673-6338.2013.02.007)
(  0) 0) |
| [6] |
广伟, 李玮, 袁海波. TGD改正对北斗授时性能的影响[C].中国卫星导航学术年会, 南京, 2014 (Guang Wei, Li Wei, Yuan Haibo. The Benefit of TGD Correction in Beidou Timing Performance[C]. China Satellite Navigation Conference, Nanjing, 2014)
(  0) 0) |
| [7] |
Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5): 1-19
(  0) 0) |
| [8] |
于合理, 郝金明, 谢建涛, 等. 硬件延迟偏差对卫星钟差解算的影响[J]. 导航定位学报, 2015, 3(1): 71-73 (Yu Heli, Hao Jinming, Xie Jiantao, et al. Impact of DCB on the Estimate of Satellite Clock Bias[J]. Journal of Navigation and Positioning, 2015, 3(1): 71-73 DOI:10.3969/j.issn.2095-4999.2015.01.015)
(  0) 0) |
| [9] |
阮仁桂. GPS非差相位精密单点定位研究[D].郑州: 信息工程大学, 2009 (Ruan Rengui. Study on GPS Precise Point Positioning Using Un-Differenced Carrier Phase[D]. Zhengzhou: Information Engineering University, 2009)
(  0) 0) |
| [10] |
Dach R, Hugentobler U, Fridez P, et al. Bernese GPS Software Version 5.0[M]. Bern: Astronomical Institute, University of Bern, 2007
(  0) 0) |
| [11] |
郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006 (Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006) http://cdmd.cnki.com.cn/Article/CDMD-90008-2007051629.htm
(  0) 0) |
2. Beidou Navigation Technology Collaborative Innovation Center of Henan, 62 Kexue Road, Zhengzhou 450001, China;
3. Xi'an Satellite Control Center, 28 East-Xianning Road, Xi'an 710043, China;
4. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2017, Vol. 37
2017, Vol. 37


