2. 中国地震局地壳应力研究所武汉科技创新基地, 武汉市洪山侧路40号, 430071
尽管网络工程和陆态网络项目的数据产出及分析结果已被广泛应用于地壳运动和构造变形监测之中[1-2], 但针对其观测时段优化、质量评估与可靠性分析等方面的研究相对较少[3-5]。本文借助陆态网络的连续GNSS资料来分析不同观测时长、观测周期以及时间跨度等对流动测站速率的影响, 评估流动GNSS观测站的速率精度及其可靠性, 为陆态网络项目后续建设和运行提供可靠的技术依据。
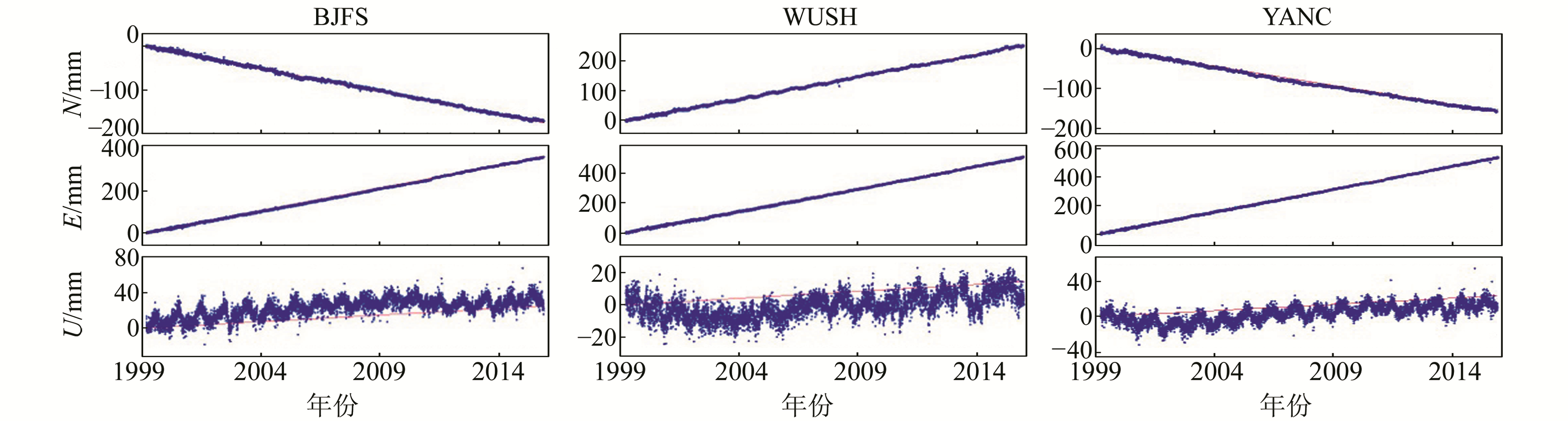
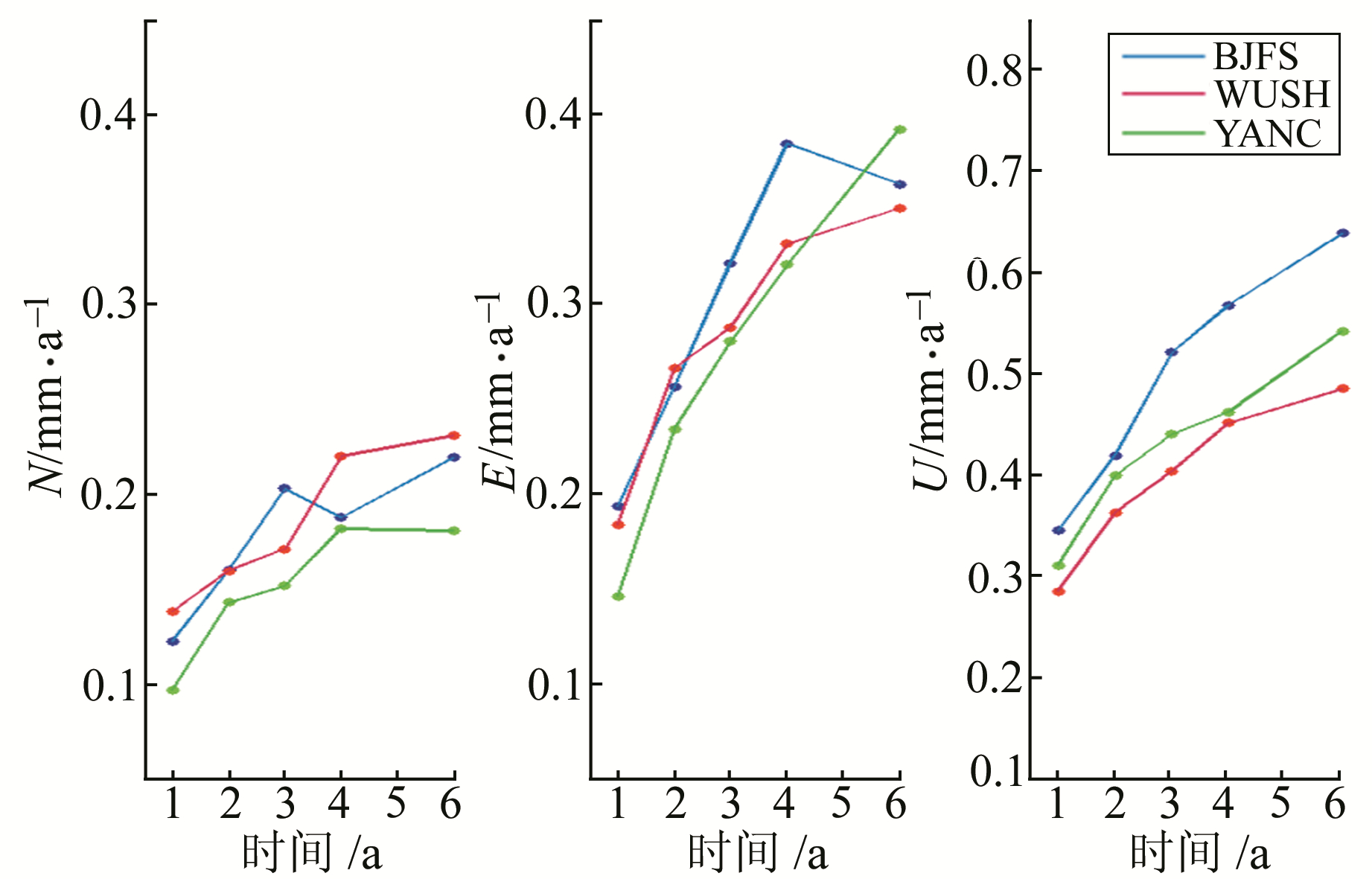
1 GNSS流动站速率的模拟方法使用Bernese软件的双差处理模式解算网络工程基准站1999~2015年的观测数据, 获得了测站相对于IGS08框架下的测站位置时间序列结果, 并改正了由于地震、仪器变更等原因引起的测站时间序列的阶跃等影响。GNSS的数据处理同以往基本一致[1], 采用Bernese软件的双差处理模式, 在处理时采用绝对天线相位中心改正、FES2004海潮模型、IGS精密星历和地球自转参数等模型。作为参考框架的站点主要是集中在欧亚板块的西伯利亚、中亚、印度板块以及中国大陆内部的IGS测站, 从中选取数据质量较好、观测时间跨度最长的BJFS、WUSH、YANC等3个站点的时间序列用于GNSS流动观测的数据模拟、速率精度与可靠性分析, 如图 1所示。由于GNSS观测会受到大气、降水等各类非构造负荷变形的影响, 其测站位置时间序列通常表现出一定的季节性变化, 因此GNSS流动观测需要同一测站的各期观测时间尽量保持一致[4-5]。
|
图 1 BJFS、WUSH、YANC站时间序列 Fig. 1 GNSS coordinate time series of BJFS, WUSH, YANC |
在数据模拟时, 第n期流动观测时间序列Tn表示为:
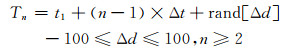
|
这里采用最小二乘方法估计各流动站时间序列的运动速率。式中, t1为第1期流动观测的时间序列; Δt为相邻2期流动观测的时间间隔; Δd表示第n期观测与第1期观测相差的天数, 用以反映每期观测时间非严格一致的时间差[4-5]。
2 观测模式对流动站速率的影响与可靠性分析 2.1 流动站时间跨度的影响为了对GNSS流动站观测的运动速率进行模拟与可靠性分析, 使用BJFS、WUSH和YANC等3个基准站进行流动站时间序列的模拟。首先分析不同观测期数(或时间跨度)对结果的影响。采用2种方案进行数据的模拟计算分析。
方案1 假定1999年开始第1期流动观测, 每1 a观测1期, 观测的期数分别为2~17期, 即对应的时间跨度为1~16 a。
方案2 假定1999年开始第1期流动观测, 每2 a观测1期, 观测的期数分别为2~9期, 即对应的时间跨度为2~16 a。
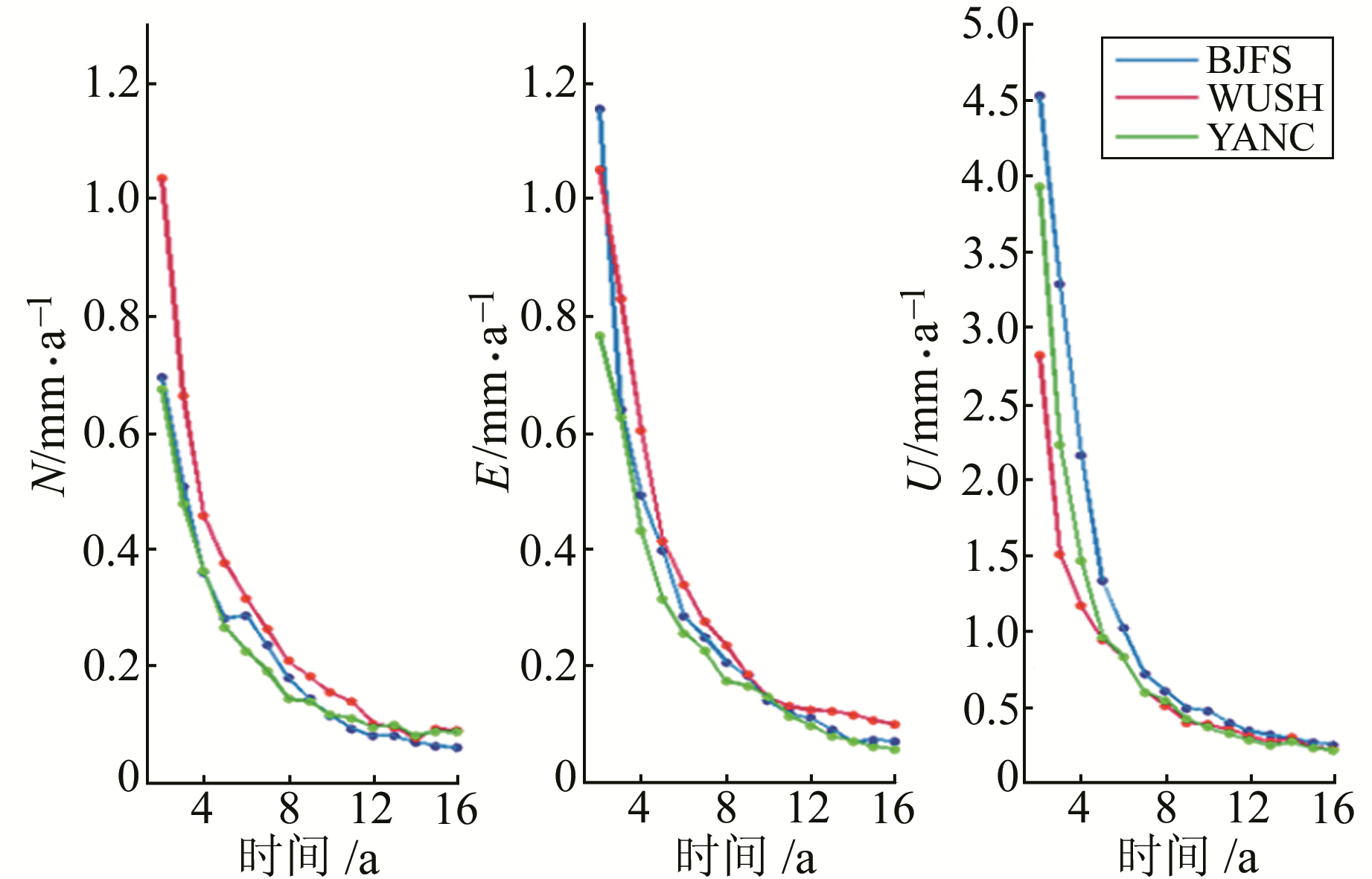
采用以上2种方案模拟500组GNSS流动站观测的时间序列, 用最小二乘方法计算其线性运动速率, 并与原始的GNSS连续站速率相比较, 计算其差异, 得到不同时间跨度下的标准差, 结果如图 2、图 3所示。
|
图 2 观测周期为1 a时时间跨度对速率差异的影响 Fig. 2 Effect of time span on difference of site rate when observation period is 1 year |

|
图 3 观测周期为2 a时时间跨度对速率差异的影响 Fig. 3 Effect of time span on difference of site rate when observation period is 2 years |
由图 2、图 3可以看出, 时间跨度对流动站速率精度的影响非常显著, 观测时间越长、期数越多, 流动站速率越接近于连续站速率。如果每1 a观测1期, 当时间跨度达到16 a时, 流动站与连续站速率差异的标准差在水平方向约为0.1 mm/a, 垂直方向约为0.2 mm/a; 如果每2 a观测1期, 当流动观测的时间跨度达到16 a时, 流动站与连续站速率差异的标准差在水平方向约为0.1 mm/a, 垂直方向约为0.3 mm/a。此外, 不论观测周期为1 a或2 a, 当流动观测的时间跨度达到10 a时, 水平方向速率差异的标准差小于0.2 mm/a, 垂直方向的速率差异小于0.5 mm/a。因此, 相对于观测周期或频次而言, 时间跨度对GNSS流动站速率精度与可靠性的影响更大。
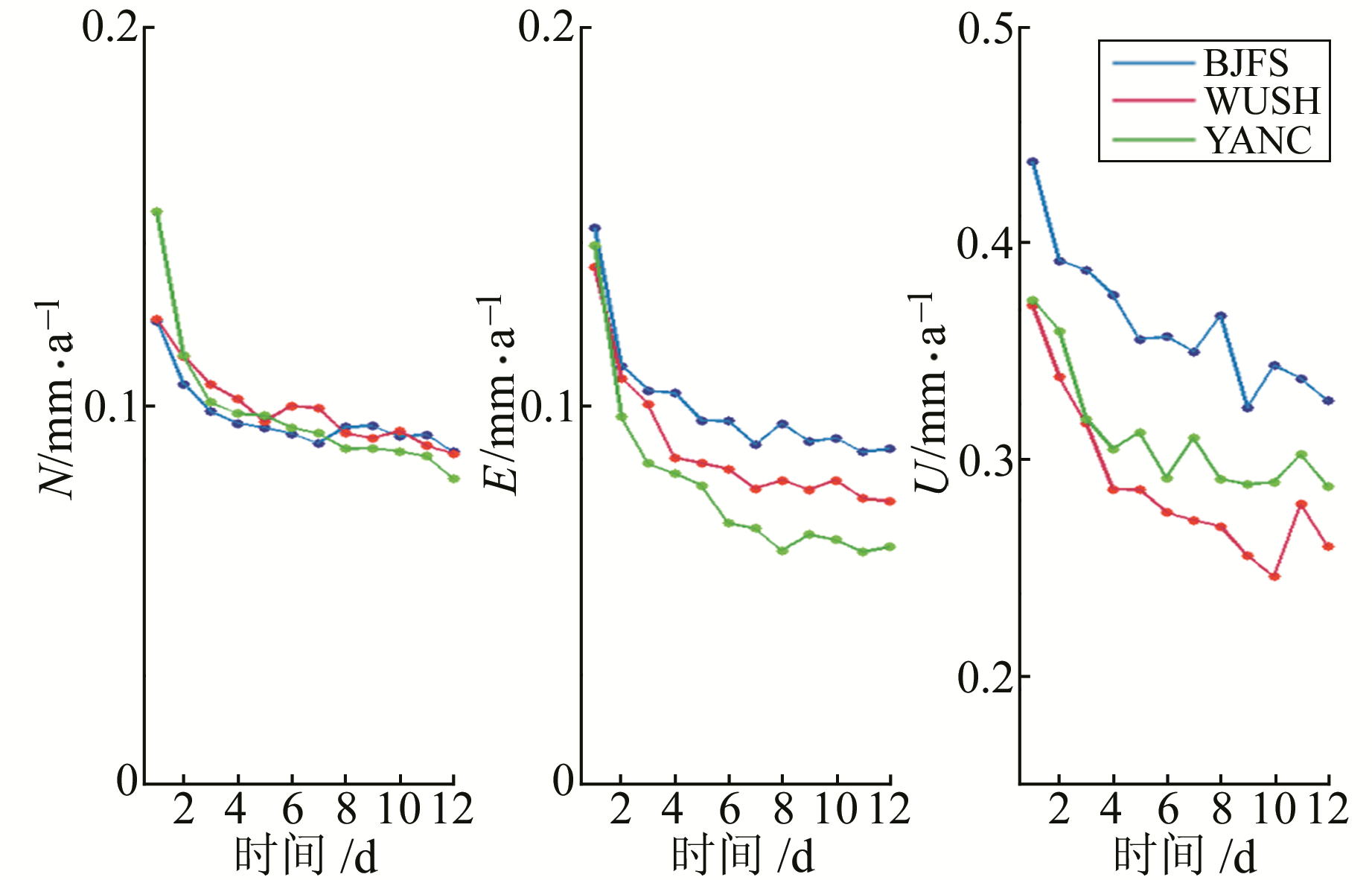
2.2 不同观测时长的影响目前网络工程和陆态网络项目GNSS流动观测站每期的观测时长为4 d。为了解每期流动观测站不同观测时长对速率精度的影响, 同样按照上文的方法, 计算观测时长分别为1~12 d时流动观测站与连续观测站的速率差及其标准差。计算分2种:第1种模拟时间跨度较长时, 观测时长对流动站速率差异的影响。这里模拟BJFS、WUSH、YANC站1999~2015年16 a的流动观测, 观测周期为2 a。第2种模拟时间跨度较短时, 观测时长对流动站速率结果的影响。模拟2009~2015年的流动观测, 观测周期同样为2 a。同样模拟了500组GNSS流动站观测的时间序列, 结果如图 4、图 5所示。

|
图 4 时间跨度为6 a时观测时长对测站速率差异的影响 Fig. 4 Effect of observation days on the difference of site rate when time span is 6 years |
|
图 5 时间跨度为16 a时观测时长对测站速率差异的影响 Fig. 5 Effect of observation days on the difference of site rate when time span is 16 years |
由图 4、图 5可以看出, 当时间跨度为6 a时, 不同观测时长对流动站水平运动的速率差异基本小于0.5 mm/a, 垂直方向小于1.5 mm/a。当观测时长大于或等于3 d时, 水平方向的速率差异小于0.4 mm/a, 垂直方向的速率差异小于1.1 mm/a。而当时间跨度为16 a时, 不同观测时长对流动站水平运动的速率差异基本小于0.15 mm/a, 垂直方向小于0.45 mm/a。当观测时长大于或等于3 d时, 水平方向的速率差异小于0.1 mm/a, 垂直方向的速率差异小于0.4 mm/a。
学者们一般利用连续站时间序列资料, 采用各类有色噪声模型分析测站运动速率及其误差[6-8]。Santamaría-Gómez等[7]分析了全球GNSS连续站的垂向位移时间序列, 利用最优噪声模型得到的全球IGS站垂直速率平均精度约为0.3 mm/a。而Wang等[8]分析了网络工程26个基准站10 a多的GNSS时间序列资料, 利用最优噪声模型得到的测站速率误差在水平方向约为0.2 mm/a, 垂直方向约为0.6 mm/a, 这一误差水平基本与时间跨度为16 a观测时长对流动站速率精度的影响相当。因此, 对于时间跨度较长的流动GNSS站点的时间序列(例如本文16 a的时间跨度), 每期流动观测的观测时长大于或等于3 d时对流动站速率的影响相对较小; 而相对于观测时长而言, 时间跨度对流动站速率精度与可靠性的影响更大。
2.3 不同观测周期的影响陆态网络项目目前的观测周期为2 a, 早期曾为3 a。为研究流动站在具有相同的时间跨度时, 不同观测周期对测站速率精度的影响, 选择BJFS、WUSH、YANC站的时间序列, 模拟2000~2012年期间的流动观测, 观测时长设为4 d, 观测周期分别设为1 a、2 a、3 a、4 a、6 a。例如观测周期为4 a, 则有2000、2004、2008、2012年4期共16 d观测数据; 而当观测周期为6 a时, 则有2000、2006、2012年3期共12 d数据。采用最小二乘方法求解其线性运动速度, 并与连续站资料得到的结果进行比较, 计算其差异的标准差。图 6为观测周期对流动观测测站速率差异的影响。由图 6可知, 在时间跨度、观测时长一定时, 观测周期越短、频次越高, 流动观测站与连续观测站的结果差异越小, 流动观测站的结果越接近于连续观测站的结果。因此, 加密观测也能有效提高流动观测的精度与可靠性[4]。
|
图 6 观测周期对测站速率差异的影响 Fig. 6 Effect of observation period on the difference of site rate |
1) 时间跨度对流动站速率精度的影响显著, 观测时间越长、期数越多, 流动站越接近于连续站的速率。按照陆态网络目前每2 a观测1期的观测模式, 当时间跨度达到16 a时, 流动站与连续站速率差异的标准差在水平方向约为0.1 mm/a, 垂直方向约为0.3 mm/a。此外, 不论观测周期为1 a或2 a, 当流动观测的时间跨度达到10 a时, 水平方向的速率差异小于0.2 mm/a, 垂直方向小于0.5 mm/a。因此, 相对于观测周期或频次而言, 时间跨度对GNSS流动站速率精度与可靠性的影响更大。
2) 当流动观测的时间跨度达到16 a时, 不同观测时长对流动站水平速率差异的影响基本小于0.15 mm/a, 垂直方向小于0.45 mm/a; 而当观测时长大于或等于3 d时, 流动观测站与连续观测站在水平方向的速率差异基本小于0.1 mm/a。
3) 在时间跨度、观测时长一定时, 观测周期越短, 流动观测与连续观测的结果差异越小, 流动观测的结果越接近于连续观测的结果。
| [1] |
王伟, 杨少敏, 赵斌, 等. 中国大陆现今地壳运动速度场[J]. 大地测量与地球动力学, 2012, 32(6): 29-32 (Wang Wei, Yang Shaomin, Zhao Bin, et al. Present-Day Crustal Movement Velocity Field in Chinese Mainland[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 29-32)
(  0) 0) |
| [2] |
王敏, 沈正康, 牛之俊, 等. 中国大陆地壳运动与活动块体模型[J]. 中国科学:地球科学, 2003, 33(增1): 21-33 (Wang Min, Shen Zhengkang, Niu Zhijun, et al. Present-Day Crustal Movement of Chinese Mainland and Active Block Model[J]. Science China:Earth Science, 2003, 33(Supp1): 21-33)
(  0) 0) |
| [3] |
王琪, 牛之俊, 石俊成. 中国地壳运动观测网络基本网观测精度研究[J]. 大地测量与地球动力学, 2003, 23(3): 9-13 (Wang Qi, Niu Zhijun, Shi Juncheng. Obsevation Precision of Basic Network of CMONOC[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 9-13)
(  0) 0) |
| [4] |
占伟, 刘志广, 苏建锋, 等. GNSS流动观测水平速度精度评估[J]. 大地测量与地球动力学, 2011, 31(5): 84-87 (Zhan Wei, Liu Zhiguang, Su Jianfeng, et al. Accuracy Evaluation of Horizontal Velocity Measured by GNSS Mobile Observation[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 84-87)
(  0) 0) |
| [5] |
丁晓光, 甘卫军, 肖根如, 等. 基于时间序列的GPS速率可靠性分析[J]. 大地测量与地球动力学, 2014, 34(1): 108-112 (Ding Xiaoguang, Gan Weijun, Xiao Genru, et al. Analysis on Reliability of GPS Rate with Time Series[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 108-112)
(  0) 0) |
| [6] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [7] |
Santamaría-Gómez A, Bouin M N, Collilieux X, et al. Correlated Errors in GPS Position Time Series: Implications for Velocity Estimates[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B1)
(  0) 0) |
| [8] |
Wang W, Zhao B, Wang Q, et al. Noise Analysis of Continuous GPS Coordinate Time Series for CMONOC[J]. Advances in Space Research, 2012, 49(5): 943-956 DOI:10.1016/j.asr.2011.11.032
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2017, Vol. 37
2017, Vol. 37

