以点质量模型为代表的“等效虚拟”方法在确定地球外部重力场时具有核函数简单、可对扰动重力场进行分频逼近、能简单地顾及地形起伏等优点[1-2], 但该方法往往局限于局部地区重力场的研究[3]。随着研究范围的扩大, 很难完成线性方程组的快速解算, 因此, 超高阶系数矩阵的存储和大型线性方程组的快速解算是目前限制点质量模型广泛使用的主要因素。文献[2, 4-5]对此进行了研究, 但未能给出高效的解算方式。本文结合文献[4]提出的方法对点质量模型的构建进行改进, 给出构建不同分辨率点质量的最佳窗口半径, 并以空中扰动引力的大范围计算为例进行实验。结果表明, 该方法在普通硬件设备上也能明显提高大规模解算效率。
1 大范围点质量模型构建 1.1 基本方程由地面重力异常观测数据解算点质量的边值条件方程[6-7]简写如下:
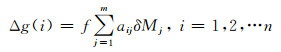
|
(1) |
其中,
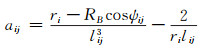
|
(2) |
式中, f为引力常数, δMj为第j个扰动质点的质量, ri为第i个观测点到球心的距离, lij为第i个观测点到第j个扰动质点之间的距离, RB=R-D为贝亚哈马球半径, D为扰动质点埋藏深度。将式(1)写成矩阵方程:
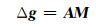
|
(3) |
解向量M为:
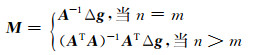
|
(4) |
求出点质量后, 可根据重力位的泛函关系进一步得到空中扰动引力三分量的计算公式:
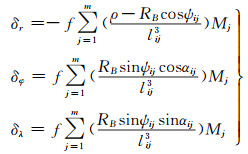
|
(5) |
式中, αij为以计算点i的北方向起算的点质量Mj的方位角, ψij和αij按下式计算得到:
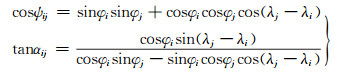
|
(6) |
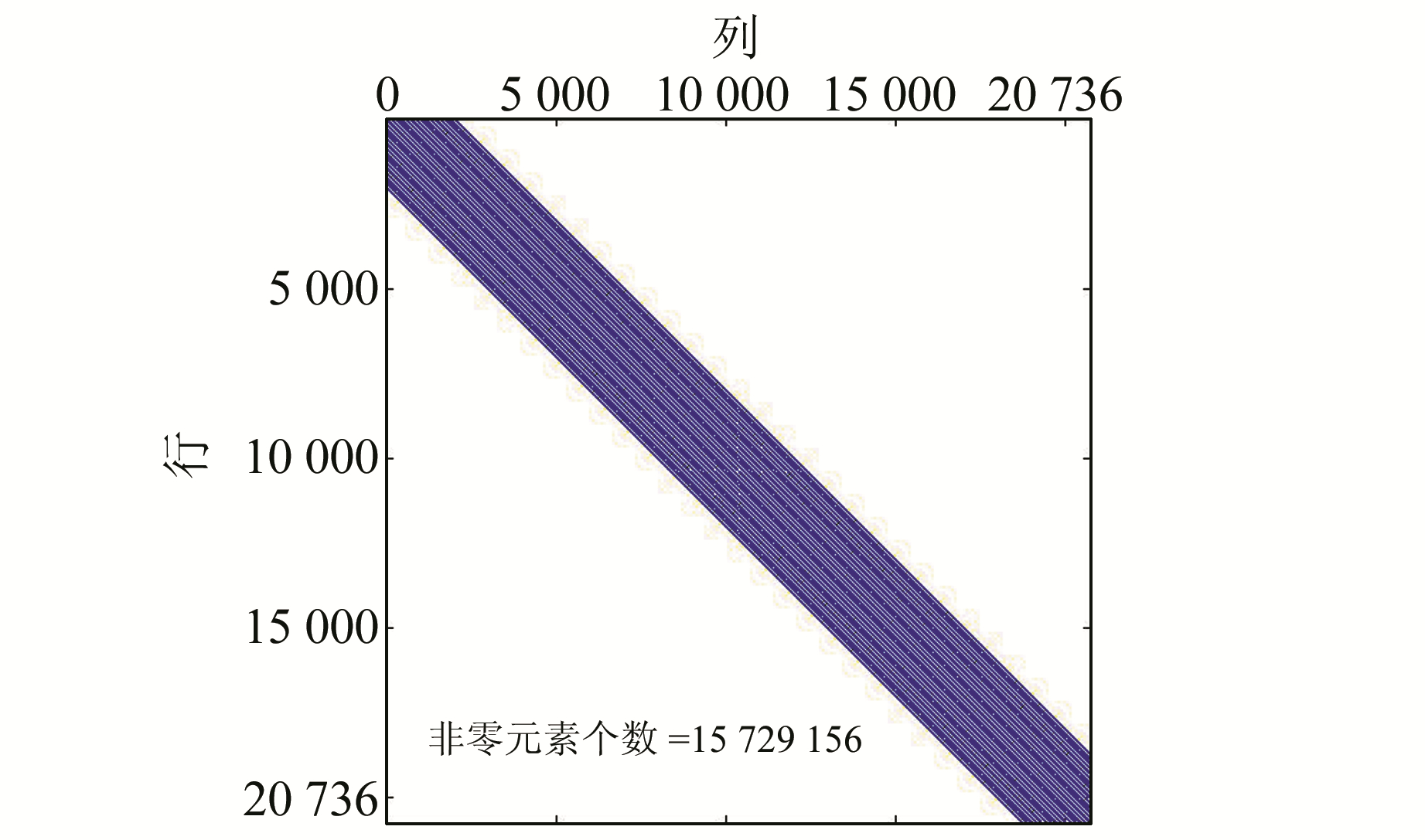
图 1(a)~(d)分别给出了点质量间隔为1°、20′、5′、1′时, 系数aij随两点间球心角距变化的关系。可以看出, 对一个位置固定的点质量, 随着点质量与观测点间距离的增大, 点质量对观测点的影响逐渐减小; 增大到一定程度后, 其影响逐渐接近于0, 甚至可忽略不计。从谱分析的角度看, 如果把重力异常中的长波部分去掉, 得到的残差重力异常可认为只受局部地区的影响, 从而将点质量对重力异常的影响控制在一定范围内。因此, 构建点质量模型时可选取合适的窗口来约束点质量的分配, 窗口之外的影响为0(称为“窗口控制法”)。采用窗口控制法进行点质量模型的解算, 其目的有2个:一是矩阵A由原来的满矩阵变成带状稀疏矩阵(图 2), 稀疏矩阵的压缩存储节省了大量内存, 有助于在特定的硬件环境下扩大点质量的整体解算范围; 二是大型稀疏线性方程的解算能够在很短时间内完成, 即使观测点个数远大于点质量个数, 也可以快速求出点质量的最小二乘解。

|
图 1 系数aij与球心角距ψ的关系 Fig. 1 Variation of coefficient aij with angle ψ |
|
图 2 带状稀疏矩阵 Fig. 2 Band sparse matrix |
基于窗口控制法的点质量模型可表示为[4]:
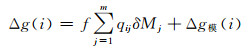
|
(7) |
其中,

|
式中, (φi, λi)为地面重力异常点Δg(i)的坐标, (φj, λj)为扰动质点δMj的坐标, ρ为窗口半径(可结合图 1中系数变化趋势通过实验得到), Δg模(i)为重力异常的长波部分, 可由高精度的低阶重力场模型求得。
事实上, 基于窗口控制的点质量模型与用Stokes积分法计算扰动场元的原理是一致的, 即在内区采用球冠积分(积分半径为ψ0), 在外区采用位系数模型[8]。因为远区的重力异常只影响待求元素的长波部分, 而这完全可用高精度的低阶位系数模型来代替。
不同分辨率的点质量模型可以表征不同波长的扰动重力场, 在实际应用中一般先选取一个低阶(N=36)重力场模型作为参考场, 以其与实际观测量的残差生成残差点质量, 然后以逐级残差的形式生成不同分辨率的残差点质量[6]。根据式(7)求解残差点质量时, 可以更好地体现出重力异常的中高频部分对待求元素的局部影响。
1.3 稀疏矩阵的行压缩存储行压缩存储法(compressed sparse row, CSR)是一种常用的压缩存储方式, 对于一个维数为m、非零元素个数为nnz的稀疏矩阵, 应用CSR格式存储时, 需要用3个一维数组:与矩阵A相同数据类型的数组val, 用来保存稀疏矩阵中的所有非零元素值, 其长度为nnz; 用来存储每个非零元素在原稀疏矩阵中的列索引的整型数组col, 其长度为nnz; 用来表示原矩阵中每行的第1个非零元素在val数组中的索引号的整型数组rowptr, 其长度为m+1(第m+1个值用来标识结束位置)。稀疏矩阵A的CSR存储方式(索引从0开始)如下所示:

|
窗口半径的大小直接影响点质量的解算范围和实际应用效果。为了给出不同分辨率的点质量计算所需的最佳窗口半径, 分别用1°×1°、20′×20′、5′×5′、1′×1′的重力异常数据计算3组点的质量结果:1)取窗口半径ρ=12(为方便对不同分辨率窗口半径的统一表述, 此处的窗口半径用待求点质量为中心的周围格网点数来代替, 下同); 2)取窗口半径ρ=15;3)取窗口半径ρ=20。
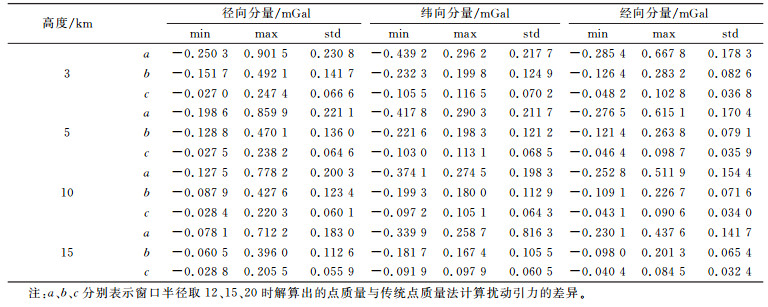
分别用上述3组结果计算不同高度处的扰动引力, 并与传统点质量法的计算结果进行比较。为了保证窗口半径在不同地区的通用性, 选取重力异常变化比较剧烈的地区进行实验(在30°~36°N、101°~107°E区域内采用2 160阶EGM2008模型生成5′×5′的重力异常数据, 并生成同等分辨率的点质量模型; 在实验中心区2°40′×2°40′范围内, 以8′×8′的网格密度计算4个不同高度上的扰动引力)。限于篇幅, 这里仅列出基于窗口控制的5′×5′点质量与传统方法生成的点质量计算扰动引力的差异, 见表 1。
|
|
表 1 窗口控制法与传统点质量法计算结果的差异 Tab. 1 The difference of window control method and traditional method |
从表 1可以看出, 选取合适的窗口半径解算的点质量与传统方法解算的点质量在计算扰动引力时的差异非常小, 而且随着计算高度的增加, 因窗口半径变化而引起的扰动引力三分量的差异逐渐减小。这主要是因为扰动引力随高度的增加不断衰减, 因此由窗口半径产生的误差对扰动引力的影响也逐渐减弱。结合图 1中系数aij与球心角距ψ的关系, 分析不同分辨率数据的实验结果发现, 对不同分辨率的数据取表 2给定的窗口半径求解点质量, 既能满足计算精度又能扩大解算范围。
|
|
表 2 不同分辨率数据对应的最佳窗口半径 Tab. 2 The best window radius of different data resolution |
本文在进行上述实验时发现, 用点质量计算扰动引力或重力异常时, 整体范围内的点质量对计算点的影响和以计算点为中心一定范围内的点质量对其影响的差异是非常小的。因此, 可根据实际应用中对计算效率的要求适当选取点质量的应用范围, 以尽可能满足实时计算的要求。这一结论与文献[4]是一致的。
2.2 窗口控制法的实际应用效果为验证基于窗口控制的分层残差点质量模型的实际应用效果, 在表 3所列区域计算了三层残差点质量(窗口半径参见表 2)。
|
|
表 3 三层残差点质量模型构建范围 Tab. 3 Research area of three-tier point mass model |
该实验区重力场信息比较丰富, 用2 160阶EGM2008模型计算出的5′×5′重力异常变化范围为-195.03~265.01 mGal, 具有一定的代表性。实验中心区5′×5′和20′×20′重力异常变化见图 3(a)和图 3(b)。

|
图 3 实验区重力异常数值分布 Fig. 3 The gravity anomaly data of the research area |
根据解算出的残差点质量在中心区域24°×24°范围内以8′×8′格网密度, 计算8个不同高度上(每个高度上共计算32 400个格网点)的扰动引力三分量。以2 160阶EGM2008模型计算出的扰动引力值作为参考值进行比较, 具体计算结果见图 4和表 4。
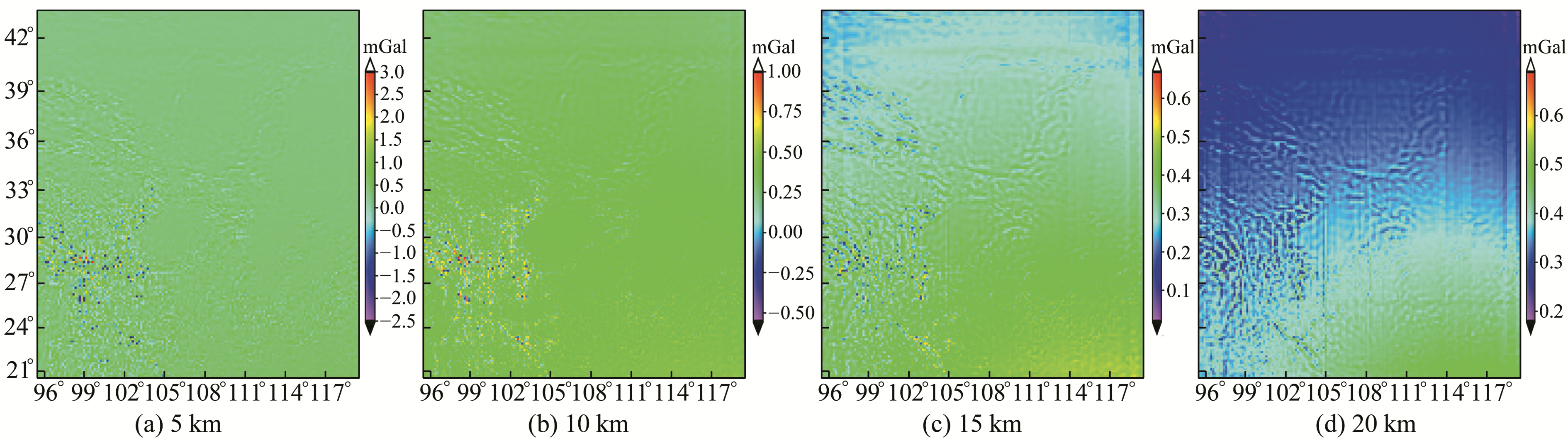
|
图 4 窗口控制法与位模型法在径向分量的差值分布 Fig. 4 The radial error distribution of window control method and model method |
|
|
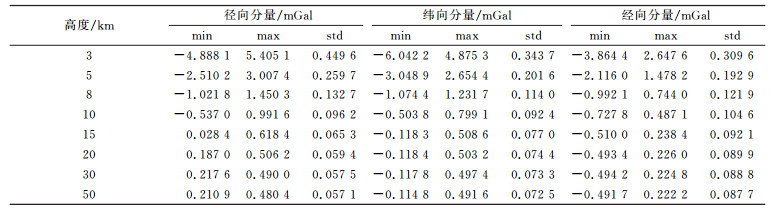
表 4 窗口控制法与位模型法的差异 Tab. 4 The difference of window control method and model method |
图 4(a)~(d)反映了以径向分量为例, 基于窗口控制的残差点质量和位系数模型在5 km、10 km、15 km、20 km高度计算结果的差异。从图 4可以看出, 随着计算高度的增加, 这种差异逐渐减小, 甚至可以忽略不计。
表 4给出了窗口控制法与位模型法计算不同高度上扰动引力三分量的差异。可以看出, 窗口控制法与位系数模型法的计算结果几乎是一致的, 高度越高, 一致性越好。只在低空(小于等于5 km)2种方法的差异较明显, 这可能是受球近似误差、位模型的截断误差以及点质量以离散化形式描述重力场的误差的影响较大。在实际应用中可通过加密高频重力数据, 叠加1′×1′的点质量层来提高低空扰动引力计算的精度。图 4和表 4的统计结果再次表明, 基于窗口控制的残差点质量模型的计算结果是可靠的。
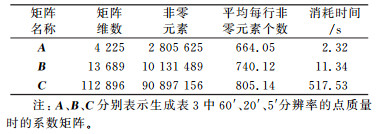
2.3 稀疏线性方程的解算构建点质量模型时涉及到大型线性方程组的解算, 采用窗口控制法可将稠密线性方程转化为稀疏线性方程。对系数矩阵进行压缩存储, 调用现有的稀疏线性运算库即可完成解算。本文对大型稀疏线性方程的解算是调用Intel MKL(math kernel library)科学计算库中的稀疏线性方程求解函数Pardiso完成的。实验所用计算机处理器为Intel CORETM i5, 主频2.3 GHz, 内存8 GB。方程的规模及解算所需时间见表 5。
|
|
表 5 稀疏线性方程解算信息统计 Tab. 5 Information of sparse linear solve with various matrix size |
如果采用传统方法构建点质量模型, 生成的系数矩阵是满矩阵, 普通计算机很难完成6 000阶以上线性方程的求解。而基于窗口控制的点质量模型将系数矩阵转化为稀疏矩阵并压缩存储, 不仅极大地降低了对计算机内存的消耗, 而且提高了计算效率, 在普通计算机上也可完成112 896阶大型方程的解算。
3 结语本文提出一种大范围点质量模型整体构建的方法——基于窗口控制的残差点质量模型。该方法以逐级残差的形式将重力异常的相关性控制在一定的范围内, 将点质量模型的求解由原来的稠密线性方程转化为稀疏线性方程, 有利于扩大点质量的整体解算范围, 提高解算效率。通过实验得到了生成不同分辨率的点质量模型所需的最佳窗口半径, 该半径在重力异常变化剧烈的地方仍具有较好的适用性。
| [1] |
管泽霖, 管铮, 黄谟涛, 等. 局部重力场逼近理论和方法[M]. 北京: 测绘出版社, 1997 (Guan Zelin, Guan Zheng, Huang Motao, et al. Theory and Method of Local Gravity Filed Approximation[M]. Beijing: Surveying and Mapping Press, 1997)
(  0) 0) |
| [2] |
吴星, 张传定, 赵东明. 基于球面边值问题的点质量调和分析方法[J]. 地球物理学报, 2009, 52(12): 2993-3000 (Wu Xing, Zhang Chuanding, Zhao Dongming. Point Mass Harmonic Analysis Method Based on Spherical Boundary Value Problem[J]. Chinese Journal of Geophysics, 2009, 52(12): 2993-3000 DOI:10.3969/j.issn.0001-5733.2009.12.008)
(  0) 0) |
| [3] |
李建成, 陈俊勇, 宁津生. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003 (Li Jiancheng, Chen Junyong, Ning Jinsheng. The Earth Gravity Field Approximation Theory and China's 2000 Quasi-Geoid Determination[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [4] |
黄谟涛, 管铮, 欧阳永忠. 中国地区1°×1°点质量解算与精度分析[J]. 武汉测绘科技大学学报, 1995, 20(3): 257-262 (Huang Motao, Guan Zheng, Ouyang Yongzhong. Accuracy Analysis and Calculation of 1°×1° Point Mass in the Area of China[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 20(3): 257-262)
(  0) 0) |
| [5] |
黄谟涛. 扰动质点赋值模式结构优化及序贯解法[J]. 测绘学报, 1994, 23(2): 81-89 (Huang Motao. Configuration Optimization of the Disturbing Point Mass Model and Its Sequential Solution[J]. Acta Geodaetica et Cartographica Sinica, 1994, 23(2): 81-89 DOI:10.3321/j.issn:1001-1595.1994.02.001)
(  0) 0) |
| [6] |
陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996 (Lu Zhonglian. Theory and Method of the Earth's Gravity Field[M]. Beijing: PLA Press, 1996)
(  0) 0) |
| [7] |
吴晓平. 局部重力场的点质量模型[J]. 测绘学报, 1984, 13(4): 249-258 (Wu Xiaoping. Point-Mass Model of Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(4): 249-258 DOI:10.3321/j.issn:1001-1595.1984.04.002)
(  0) 0) |
| [8] |
夏哲仁, 盛宗琪, 李迎春. 外空扰动引力场的传播特性[J]. 地球物理学报, 1998, 41(4): 484-493 (Xia Zheren, Sheng Zongqi, Li Yingchun. Propagation Properties of Disturbing Gravity Field Outside the Earth[J]. Chinese Journal of Geophysics, 1998, 41(4): 484-493 DOI:10.3321/j.issn:0001-5733.1998.04.007)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37