2. 中国测绘科学研究院, 北京市莲花池西路28号, 100830;
3. 中国科学院测量与地球物理研究所, 武汉市徐东大街340号, 430077;
4. 中国科学院大学, 北京市玉泉路甲19号, 100049
本文根据地球重力场的物理特性, 提出一种基于Gauss-Listing大地水准面经典定义的地球重力场模型评价方法, 并给出了重力位标准差作为评价指标。首先介绍了地球重力场模型常用的评价方法及其存在的问题, 随后给出了基于经典大地水准面定义的地球重力场模型评价方法的基本思想和实现关键, 最后利用实验验证了该方法的有效性。
1 常用评价方法常用的地球重力场模型评价方法包括模型位系数阶方差, 以及利用模型解算得到的重力场元与实测值比较, 如重力异常、高程异常、垂线偏差等[1-3]。模型位系数阶方差en表示为:
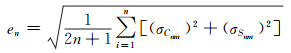
|
(1) |
式中, σCnm和σSnm分别为相应阶次模型位系数的中误差。
该方法需要准确可靠的位系数中误差, 在模型解算时要构建观测量与模型位系数之间准确的协方差函数, 并利用最小二乘法进行模型解算。由于融合多源重力场观测数据恢复高阶地球重力场模型时存在协方差构建和超高阶法方程解算的困难, 致使解算得到的模型位系数中误差的准确性和可靠性无法保证。在实际应用中, σCnm和σSnm也常用解算模型与参考模型的位系数之差代替, 用于表示解算模型与参考模型之间的差异。
重力异常误差和高程异常误差评价方法为:
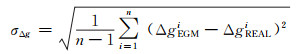
|
(2) |
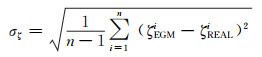
|
(3) |
式中, ΔgEGMi、ζEGMi分别为检验区域计算点模型重力异常和模型高程异常, ΔgREALi、ζREALi为相应点的实测重力场元, n为检验区域的总点数。
由于地球重力场模型构建时, 其位系数是对大地水准面平均格网重力异常的全球积分, 因此利用模型解算得到的计算点重力异常理论上为该点所在区域相应格网的平均重力异常, 与该点的实测重力异常存在代表性误差。此外, 鉴于引力位的球谐函数表达与Stokes积分公式的等价性, 模型地面点高程异常的确切物理意义是过该点处等位面的“当地”水准面差距, 即Molodensky意义下的高程异常零阶项, 而非实测的具有全频谱特性的高程异常。因此, 重力异常误差、高程异常误差的评价方法都存在理论上的不严密性[1]。
2 大地水准面经典定义及其应用Gauss-Listing于19世纪给出大地水准面的经典定义即是与平均海水面最佳拟合的重力等位面。实践证明, 该经典定义在应用中存在2个方面的缺陷:一是由于海流和海洋潮汐的存在, 难以得到排除所有动力学影响的平均海平面; 二是严格意义上平均海水面并不是重力等位面[4-5]。随后提出了“理想的海洋面”、“无干扰的平均海面”以及“海面地形平均值为零”等大地水准面定义, 旨在从根本上克服经典大地水准面定义的理论缺陷[6]。基于广义相对论原理, Bejerhammar、申文斌等[7-8]提出等时率和等频相对论大地水准面, 更加符合大地水准面的等位面特性, 但在实现上需要高稳定度频标。晁定波、魏子卿等[9-10]基于大地水准面的理论特性, 提出一个理论严密且可实现的全球大地水准面定义:大地水准面是一个与纳入到统一潮汐系统的某一历元全球平均海面最佳拟合的重力等位面。所谓最佳拟合是指大地水准面上的位常数W0等于一个格网化全球平均海面模型所有格网中心点重力位值的均值, 并在全球保持位常数不变, 全球平均海平面的重力位值由一个具有相应分辨率的全球重力位模型确定。该定义不仅符合大地水准面的理论特性, 明确了大地水准面与地球重力场模型的关系, 且具有可唯一实现性。
Gauss-Listing大地水准面经典定义虽然实现困难, 但是不失其理论价值, 即大地水准面的重力等位面特性, 之后的各种改进的大地水准面定义都紧扣了大地水准面作为重力等位面的物理特性。根据晁定波等[9]提出的全球大地水准面定义的最佳拟合原则可知, 大地水准面上的位常数W0等于全球平均海面模型上重力位值的均值, 该全球平均海面的重力位值源于某一全球重力位模型。由Gauss-Listing大地水准面经典定义可知, 作为重力位等位面的大地水准面上的重力位应为恒定值, 其标准差理论上为0, 实际上的非零反映了地球重力场模型的理论表达能力。由于地球重力场模型误差的存在, 格网化全球平均海面模型所有格网中心点重力位值Wi与其均值W0必然存在一定的偏差, 其离散情况反映了大地水准面与平均海面模型之间的拟合程度, 即标准差越小说明地球重力场模型理论符合度越优。
因此, 本文基于Gauss-Listing大地水准面经典定义和晁定波等提出的全球大地水准面定义, 提出了利用大地水准面上重力位标准差作为地球重力场模型精度优劣的评价方法。具体表述为:选取某局部或全球大地水准面作为重力等位面的参考面, 以格网点形式表达, 利用地球重力场模型计算该参考面上对应格网点的重力位Wij, 其平均重力位值为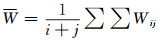
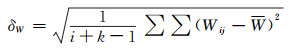
|
(4) |
该方法不仅可用于不同地球重力场模型间的比较, 也可评价同一地球重力场在全球不同区域的表达能力。
3 算例分析本文涉及到的地球重力场模型包括OSU91A、EGM96、ITG-GRACE03、EGM2008、EIGEN-6C4、GOCO05S等, 各模型的基本情况及参考椭球信息详见表 1[4, 11-12]。
|
|
表 1 本文研究所用的地球重力场模型 Tab. 1 Earth gravitational models and their parameters used in present study |
其中, OSU91A模型和EGM96模型是综合利用当时卫星测高数据和地面重力测量数据以及地形信息组合构建的完全阶次到360的地球重力场模型, 后者增加了DORIS跟踪数据和更长时序的卫星测高数据, 其精度全面优于前者。EGM2008模型和EIGEN-6C4模型是综合利用地面重力、卫星测高和卫星跟踪以及卫星重力观测数据构建的完全阶次到2 160的地球重力场模型, 其中前者的最高阶数扩展到2 190, 全波段大地水准面精度约为十几cm, 后者增加了2009-11-01~2013-10-20的GOCE卫星观测数据, 理论阶方差显示其精度要优于前者, 利用GPS水准检核表明其大地水准面精度与前者相当[13]。各模型的大地水准面阶次误差如图 1所示, 其中高阶模型仅显示到360阶。
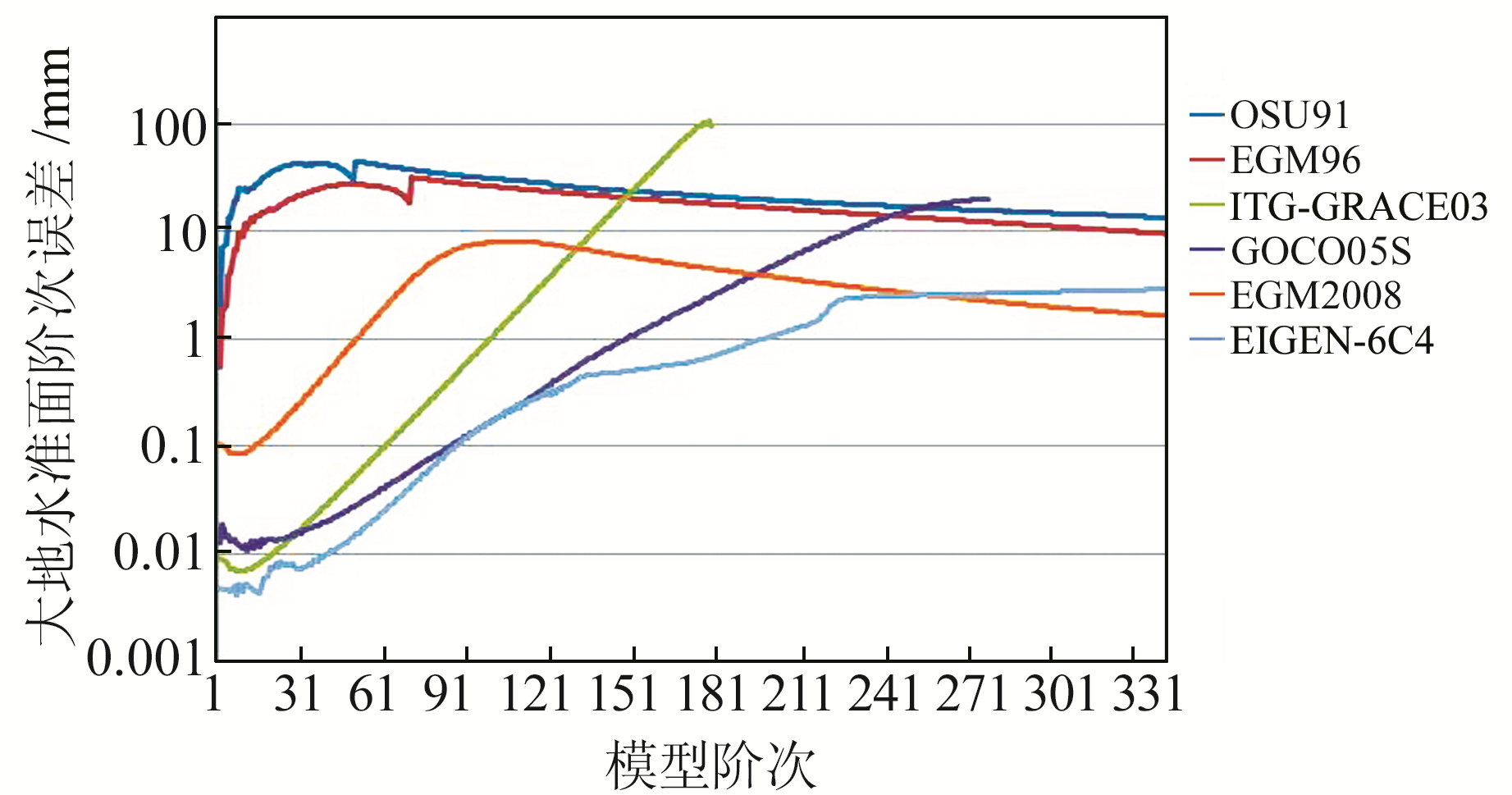
|
图 1 不同地球重力场模型大地水准面阶次误差 Fig. 1 Geoid degree RMS of different EGMs |
本文选取太平洋某区域卫星测高获得的平均海平面作为全球重力等位面的代表区域, 用于地球重力场模型优劣评价。选取的平均海平面区域范围为15°~20°N、150°~155°E, 分辨率为1′×1′, 共计90 000个点。该区域的平均海面大地高最小为28.855 0 m, 最大为46.631 0 m, 平均为38.035 6 m, 对应的地球参考椭球长半轴为6 378 136.3 m, 扁率为1/298.275。该模型为实测海面大地高扣除海潮等影响后得到的平均静止海平面, 进行海面地形影响改正后可视为海洋大地水准面(图 2)。

|
图 2 区域平均海平面模型 Fig. 2 Local average sea surface model |
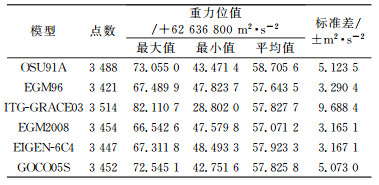
因不同地球重力场模型采用的参考椭球不同, 地球重力场模型采用的参考椭球参数与所选取的平均海平面模型采用的参考椭球参数也不同, 在实际计算中, 必须进行参考椭球基准的统一。具体转换方法为:1)将平均海平面模型计算点(B, L, H)由其对应的参考椭球转换到地球重力场模型对应的参考椭球下, 得到新的计算点(B′, L′, H′); 2)利用地球重力场模型计算新的计算点在地球重力场对应地球参考椭球下的重力位值及平均重力位值; 3)利用式(4)计算该地球重力场模型在平均海平面上的重力位标准差。利用上述步骤即可得到不同地球重力场模型在该区域平均海平面上的重力位标准差, 计算结果见表 2。
|
|
表 2 区域平均海平面重力位值及其标准差 Tab. 2 MSL potentials and dispersions of different EGMs |
由表 2可见, 在该平均海平面区域, OSU91A模型、EGM96模型的重力位标准差分别为±5.123 5 m2 ·s-2和±3.290 4 m2 ·s-2, 说明EGM96模型要优于OSU91模型; EGM08模型、EIGEN-6C4模型的重力位标准差分别为±3.165 1 m2 ·s-2和±3.197 1 m2 ·s-2, 说明这2个模型的精度相当且优于其他模型; ITG-GRACE03模型、GOCO05S模型的重力位标准差分别为±9.688 4 m2 ·s-2和±5.073 0 m2 ·s-2, 说明这2个模型的精度相对较差, 这与其阶次较低、对实际地球重力场的精细结构表达能力有限有关。此外, 比较EGM2008模型和GOCO05S模型的重力位标准差可知, 虽然阶方差显示在低阶部分GOCO05S模型要优于EGM2008模型, 但是对于实际地球重力场的表达能力而言EGM2008模型要优于GOCO05S模型, 显示了地球重力场模型精度与分辨率的辩证关系。
3.2 基于区域陆地大地水准面的模型分析选取陆地上某区域高精度重力大地水准面作为参考面。该区域为综合利用EGM2008地球重力场模型、地面重力观测数据、航空重力观测数据以及地形信息确定的区域重力大地水准面, 无GPS水准数据参与模型构建, 位于27°~31°N、81°~84°W, 分辨率为30″×30″, 共计43 200个点, 大地高最小为-28.622 0 m, 最大为-22.985 0 m, 平均为-27.048 1 m, 参考椭球为GRS80。利用GPS水准进行外部检核, 该模型的大地水准面精度达到±0.8 cm, 远优于现有的高阶地球重力场模型的大地水准面累计误差, 以此作为参考面对地球重力场模型进行评价具有较高的可靠性(图 3)。
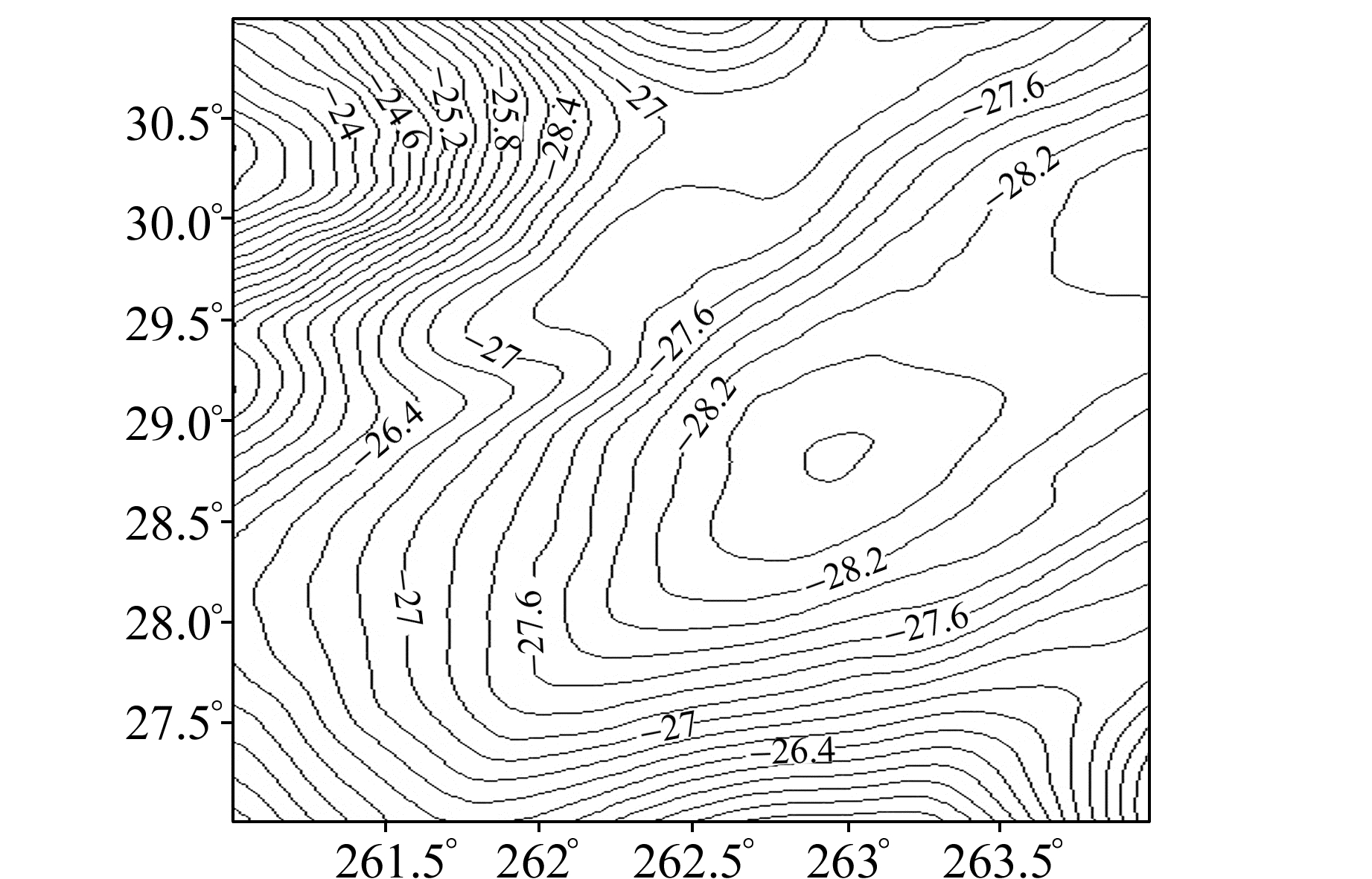
|
图 3 区域陆地大地水准面模型 Fig. 3 Local land geoid model |
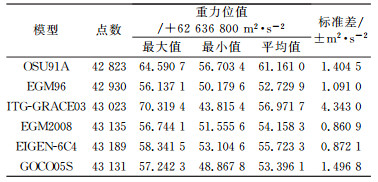
利用§3.1有关参考椭球基准的统一和重力位的计算, 即可得到不同地球重力场模型在该区域陆地大地水准面上的重力位标准差, 计算结果见表 3。
|
|
表 3 区域陆地大地水准面上重力位值及标准差 Tab. 3 Local land geoid potentials and dispersions of different EGMs |
通过各模型的重力位标准差计算结果可见, EGM2008模型、EIGEN-6C4模型精度相当且相对较优, ITG-GRACE03模型精度相对最差。
比较表 2和表 3的模型重力位标准差(如图 4所示, 其中蓝色代表区域海洋大地水准面, 红色代表区域陆地大地水准面)看出, 本文研究的6个地球重力场模型在区域陆地大地水准面的重力位标准差均小于相应的区域海洋大地水准面计算值, 说明本文选取的区域陆地大地水准面的精度要高于区域海洋大地水准面。同时6个地球重力场模型在2个参考面上的重力位标准差的大小顺序, 验证了用本文方法评价不同地球场模型精度相对优劣的可行性。
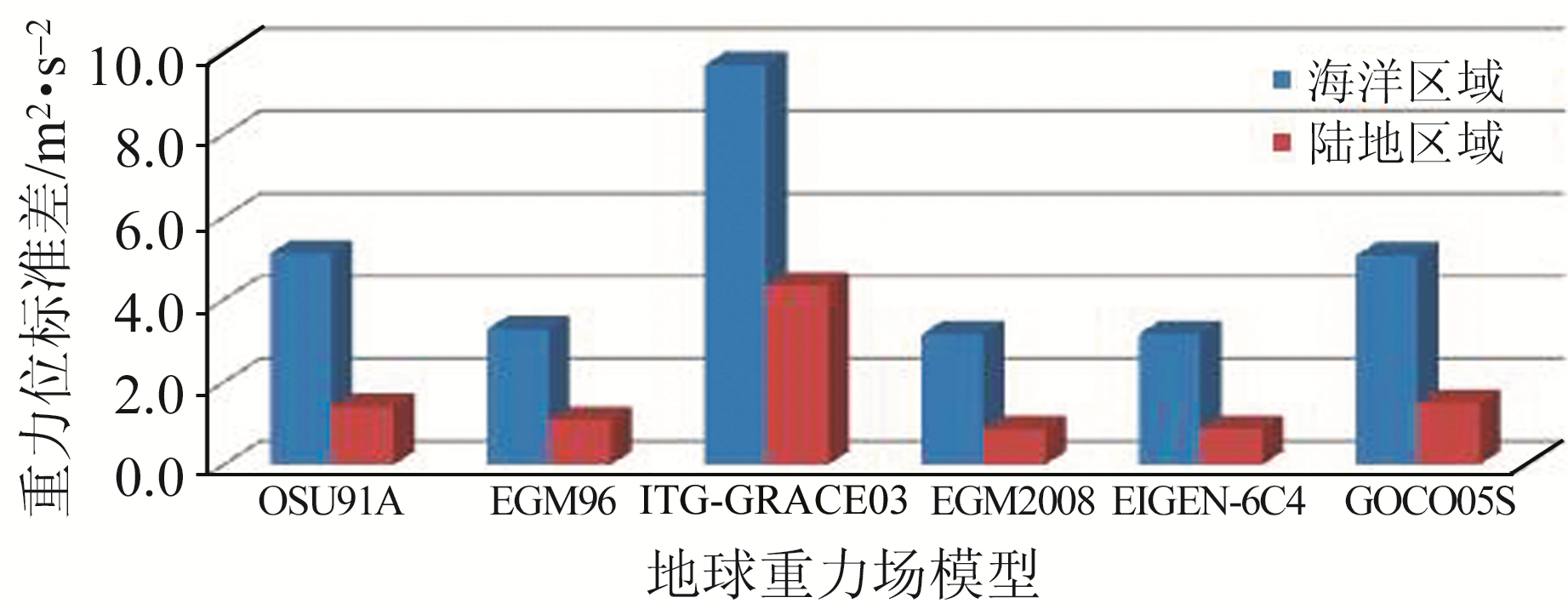
|
图 4 不同模型在不同参考面上的重力位标准差 Fig. 4 Geoid potential discrete in different geoids of different EGMs |
为进一步验证本文方法的适用性以及EGM2008模型和EIGEN6C4模型的精度优劣及在全球不同区域的精度情况, 选取国家地理空间情报局(NGA)利用地球重力场模型EGM2008直接解算得到的30″×30″分辨率的全球大地水准面作为参考面进行实验, 该大地水准面参考椭球为WGS84。
由于地球重力场模型构建的数据源在种类、精度、分辨率等方面在全球的分布差异较大, 致使同一地球重力场模型在不同区域的表达能力不同。地球重力场模型的构建利用的是全球数据, 但其应用却常常是局部的, 因此地球重力场的全球分布优劣评价既是对地球重力场模型本身优劣评价的需求, 也是地球重力场模型应用取舍的重要依据。
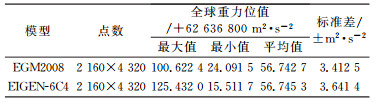
基于上述方法和流程, 分别对地球重力场模型EGM2008、EIGEN-6C4进行计算, 其全球重力位标准差见表 4。
|
|
表 4 EGM2008和EIGEN-6C4的全球重力位标准差 Tab. 4 Geopotential SD of EGM2008 and EIGEN-6C4 |
表 4中的全球重力位标准差是指地球重力场模型在全球5′×5′的格网分辨率上的标准差。根据Gauss-Listing大地水准面经典定义可知, 该格网平均重力位值应与全球大地水准面重力位值相等, 2者实际上的差异反映着模型的表达能力和大地水准面的准确度。
为进一步展示地球重力场模型在全球的表达能力, 将全球分为5°×5°的格网, 共计36×72个区域, 以模型的5′×5′格网上全球重力位值的均值为基准, 得到每个区域相对于全球重力位的标准差, 即该模型的区域重力位标准差。其全球重力位标准差分布见图 5和图 6。
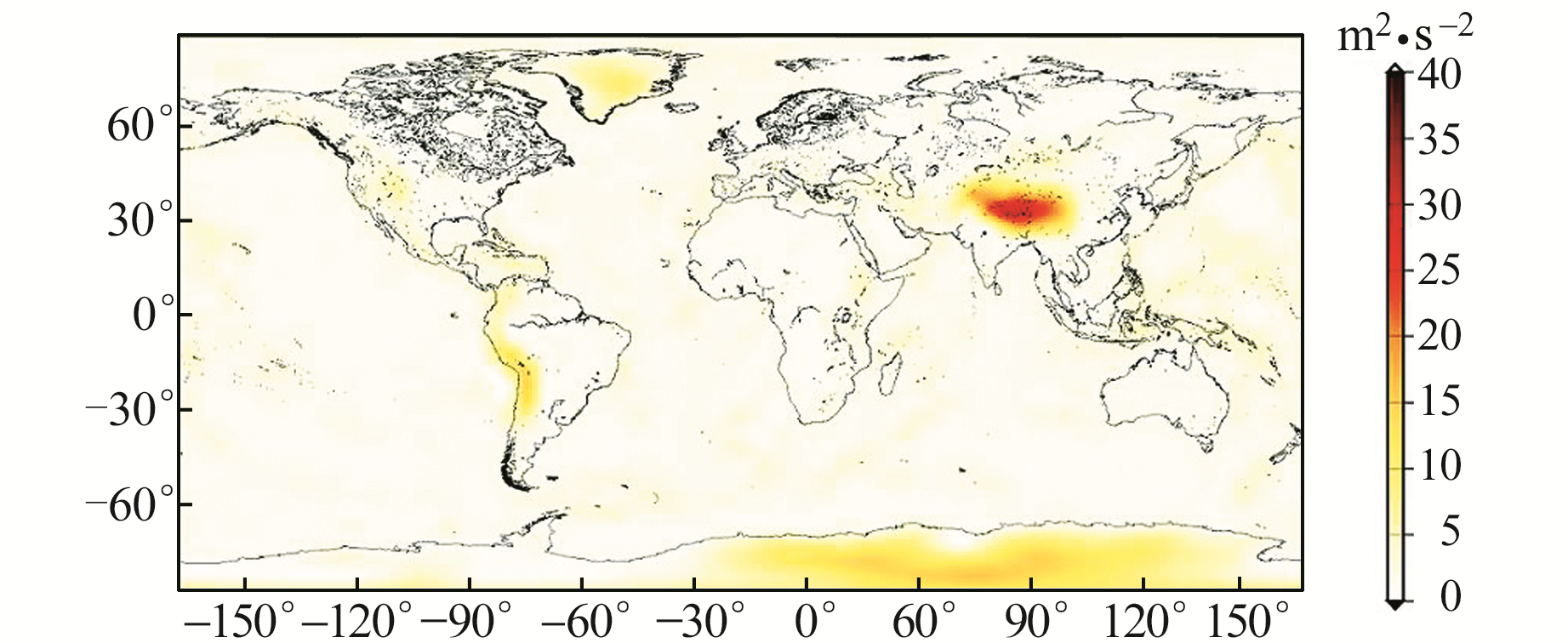
|
图 5 EGM2008全球重力位标准差 Fig. 5 Geopotential SD of EGM2008 |

|
图 6 EIGEN-6C4全球重力位标准差 Fig. 6 Geopotential SD of EIGEN-6C4 |
图 5和图 6显示, 2个模型在30°~35°N、80°~85°E(主要位于我国喜马拉雅山脉区域)重力位标准差均较大, 明显高于全球其他区域, 说明在该区域2个模型的精度均较低。
从表 4、图 5、图 6可见, EGM2008模型和EIGEN-6C4模型的大地水准面上的重力位平均值、全球重力位标准差及其全球分布情况均相当, 说明2个模型对于实际地球重力场表达的理论符合度相似。
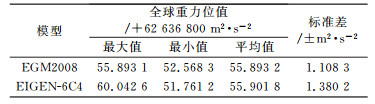
从统计学角度而言, 未剔除异常值的统计结果难以准确表达全局特性, 因此, 对2个模型5′×5′的格网重力位值按照正态分布规律剔除粗差, 处理后的全球重力位值统计结果见表 5。
|
|
表 5 剔除粗差EGM2008模型和EIGEN-6C4模型的全球重力位值及其标准差 Tab. 5 Geopotential and SD of EGM2008 and EIGEN-6C4 after eliminating gross error |
由表 5可见, 2个模型的全球重力位均值分别为62 636 855.893 2 m2 ·s-2和62 636 855.893 2 m2 ·s-2, 与IERS2010协议推荐的全球重力位值W0=62 636 856.0±0.5 m2 ·s-2的要求相符, 其重力位标准差分别为±1.108 3 m2 ·s-2和±1.380 2 m2 ·s-2。由扰动位和大地水准面高的关系可得δN=δT/γ, 其中γ取全球平均重力值9.8 m ·s-2, EGM2008模型、EIGEN-6C4模型对于大地水准面的全球平均理论表达精度分别为±0.113 1 m和±0.140 8 m, 表明在cm级精度上EGM2008模型要略优于EIGEN-6C4模型。
4 结语本文提出一种基于Gauss-Listing大地水准面经典定义的地球重力场模型优劣评价方法及重力位标准差的评价指标。鉴于参考大地水准面本身存在误差, 所以无法通过重力位标准差指标简单量化地球重力场模型的绝对精度, 但是可以通过不同地球重力场模型在同一参考大地水准面或者同一地球重力场模型在全球大地水准面不同区域的重力位标准差, 来判定不同地球重力场模型或同一地球重力场模型区域符合度的相对优劣。
本文给出了OSU91A、EGM96、ITG-GRACE03、COCO05S等具有代表性的全球重力场模型在某大地水准面区域的评价和EGM2008、EIGEN-6C4两个地球重力场模型在全球的重力位标准差分布及评价, 得出了EGM2008、EIGEN-6C4两个模型对实际地球重力场表达能力相当的结论, 2个模型表达的大地水准面的理论精度约为±11.3 cm和±14.1 cm。图 1给出的地球重力场模型位系数阶方差显示, EIGEN-6C4模型的精度略优于EGM2008模型, 但本文研究却得出了相反结论。这是因为§3.2选取的区域陆地大地水准面和§3.3选取的全球大地水准面模型在构建时均利用了地球重力场模型EGM2008, 与该模型的自洽性可能偏好, 而§3.1选取的区域海洋大地水准面作参考面完全独立于这2个模型, 依然得到同样结论, 验证了本文方法的准确性, 以及EGM2008模型精度略优于EIGEN-6C4模型的结论。
| [1] |
荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6): 123-125 (Rong Min, Zhou Wei, Chen Chunwang. Evaluation of Gravity Field Models EGM2008 and EGM96 Applied in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 123-125)
(  0) 0) |
| [2] |
邱斌, 朱建军, 乐科军. 高阶地球重力场模型的评价及其优选[J]. 测绘科学, 2008, 33(5): 25-27 (Qiu Bin, Zhu Jianjun, Le Kejun. Evaluation and Optimal Selection of High-Order Earth's Gravity Field Models[J]. Science of Surveying and Mapping, 2008, 33(5): 25-27 DOI:10.3771/j.issn.1009-2307.2008.05.008)
(  0) 0) |
| [3] |
张精明, 闫建强, 王福民. EGM2008地球重力场模型精度分析与评价[J]. 石油地球物理物探, 2010, 45(增1): 230-233 (Zhang Jingming, Yan Jianqiang, Wang Fumin. Accuracy Analysis and Evaluation of EGM2008 Earth Gravity Field Model[J]. Oil Geophysical Prospecting, 2010, 45(Supp1): 230-233)
(  0) 0) |
| [4] |
Rapp R H. The Geoid: Definition and Determation[J]. EOS Transactions American Geophysical Union, 1974, 55(3): 118-126 DOI:10.1029/EO055i003p00118
(  0) 0) |
| [5] |
Fischer I. Does Mean Sea Level Slope or Down toward North?[J]. Bulletin Geod, 1975, 115(1): 17-26 DOI:10.1007/BF02523939
(  0) 0) |
| [6] |
Shen W B, Chao D B, Jin B R. On Relativistic Geoid[J]. Bollettino di Geodesia e Scienze Affini, 1993, 52(3): 207-216
(  0) 0) |
| [7] |
Bjerhammar A. On a Relativistic Geodesy[J]. Bulletin Geod, 1985, 59(3): 207-220 DOI:10.1007/BF02520327
(  0) 0) |
| [8] |
申文斌, 宁津生, 李建成, 等. 论大地水准面[J]. 武汉大学学报:信息科学版, 2003, 26(6): 683-687 (Shen Wenbin, Ning Jinsheng, Li Jiancheng. On Geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 26(6): 683-687)
(  0) 0) |
| [9] |
晁定波, 申文斌, 王正涛. 确定全球厘米级精度大地水准面的可能性和方法探讨[J]. 测绘学报, 2007, 36(4): 370-376 (Chao Dingbo, Shen Wenbin, Wang Zhengtao. Investigations of the Possibility and Method of Determining Global Centimeter-Level Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 370-376 DOI:10.3321/j.issn:1001-1595.2007.04.003)
(  0) 0) |
| [10] |
魏子卿. 大地水准面短议[J]. 地理空间信息, 2009, 7(1): 1-3 (Wei Ziqing. Brief Introduction to the Geoid[J]. Geospatial Information, 2009, 7(1): 1-3 DOI:10.3969/j.issn.1672-4623.2009.01.001)
(  0) 0) |
| [11] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B4): 1-38
(  0) 0) |
| [12] |
Bomfim E P, Braitenberg C, Molina E C. Mutual Evaluation of Global Gravity Models(EGM2008 and GOCE) and Terrestrial Data in Amazon Basin, Brazil[J]. Geophysical Journal International, 2013, 195(2): 870-882 DOI:10.1093/gji/ggt283
(  0) 0) |
| [13] |
Tsoulis D, Patlakis K. A Spectral Assessment Review of Current Satellite-Only and Combined Earth Gravity Models[J]. Reviews of Geophysics, 2013, 51(2): 186-243 DOI:10.1002/rog.20012
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
4. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2017, Vol. 37
2017, Vol. 37