2. 地理信息工程国家重点实验室, 西安市雁塔路中段1号, 710054;
3. 信息工程大学地理空间信息学院, 郑州市科学大道62号, 450001
我国学者在重力卫星数据处理方面进行了大量研究, 采用加速度法[1-2]、能量法[3-4]、动力学法[5-6]、基线法[7]、短弧边值法[8]实现了地球重力场反演。Chen等[9-10]提出改进短弧边值法, 反演的地球重力场模型精度优于国际同类重力场模型精度水平。罗佳[11]提出交叠点法用于群低轨卫星数据处理, 有效消除了非保守力影响。宁津生等[12]将去相关滤波算法用于重力场模型解算, 较等权解算法提高了重力场模型确定的精度。万晓云等[13]采用球谐分析方法讨论了极区空白对重力场恢复的影响, 结果表明, 低阶位系数受到的影响比较显著, 采用移去-恢复方法可削弱空白带来的精度损失。在并行计算方面, 邹贤才等[14]将OpenMP并行方法应用于新一代重力卫星数据处理, 提高了数据处理效率。周浩等[15]基于MPI实现了最小二乘直接法恢复地球重力场, 计算效率提高95%。在卫星指标分析和轨道设计方面, 庞振兴等[16]采用谱分析方法分析了重力卫星在不同轨道高度的测量能力。姜卫平等[17]采用解析方法分析了重力场恢复对载荷精度的要求。钟波[18]基于时域最小二乘误差分析方法设计了卫星重力梯度测量中轨道高度、倾角、采样间隔、时间跨度、重力梯度测量精度等指标参数。郑伟等[19]基于解析模型论证了GRACE Follow-On不同载荷配置对重力场精度的影响, 并采用改进的能量法分析了GRACE星间测量系统、GPS接收机、加速度计等精度指标间的关系, 提出我国重力测量卫星测速精度为1~3 μm/s, 轨道精度为3~10 cm, 加速度精度为0.3~1 nm/s[20]。
综上分析, 新一代重力场测量卫星指标研究还较为欠缺, 特别是结合工程可行性和技术先进性的研究较弱。发展新一代重力测量卫星需要进行先期的核心指标设计。鉴于此, 本文将研究新一代重力场测量卫星的指标。本文基于边界条件分析的思想, 详细研究了新一代重力卫星的3大载荷的核心指标, 包括星间测速、非保守力测量、精密轨道测定的指标要求, 以建立新一代重力卫星核心技术指标体系, 为系统工程设计提供技术参考。
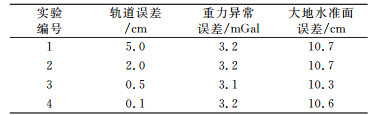
1 仿真条件设定本文采用基于边界条件的动力学分析方法, 成体系地开展重力测量卫星载荷指标实验设计。首先, 选定基准模型EIGEN6C2仿真1个月的轨道、星间距离变率、非保守力等数据; 再依据各项实验要求在观测数据上调制观测误差, 生成观测数据; 然后, 采用动力学方法处理观测数据, 反演得到重力场模型; 最后, 将反演重力场模型与基准重力场模型进行比较, 得到反演重力场模型误差, 采用大地水准面的阶误差及累积误差评估模型精度。
实验采用的主要仿真条件见表 1(将轨道高度、星间距离选择为300 km和100 km是依据先期开展的空间重力场空间分布特征研究和仿真实验的结果[16])。
|
|
表 1 仿真条件 Tab. 1 Simulation conditions |
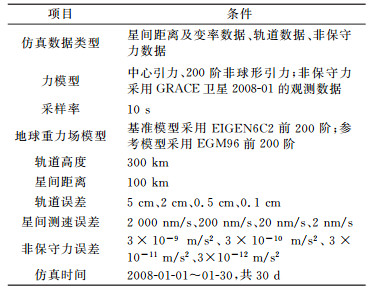
在非保守力误差和轨道误差分别为1×10-12 m/s2和1 mm的条件下, 分析星间距离变率测量误差2 μm/s、0.2 μm/s、20 nm/s和2 nm/s对重力场精度的影响。处理仿真数据, 得到地球重力场模型, 与基准模型比较获得了反演模型误差, 进一步将模型误差表示为大地水准面阶误差, 结果见图 1。相应的重力异常累积误差和大地水准面累积误差统计结果见表 2。

|
图 1 大地水准面阶误差 Fig. 1 The degree error of geoid |
|
|
表 2 星间变率误差对重力场精度的影响分析 Tab. 2 The effect on the accuracy of the gravity model from range-rate error |
分析上述结果可知, 随着星间变率测量误差的减小, 重力异常和大地水准面误差均减小。当星间距离变率误差减小到20 nm/s后, 进一步减小星间距离变率误差对重力场反演精度的提高不再明显。因此, 在目前设计的卫星配置条件下, 选择星间变率测量精度为10~30 nm/s较优。
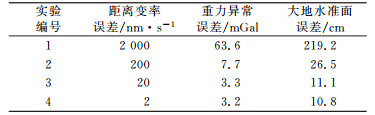
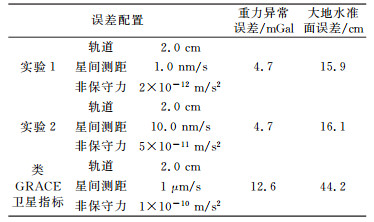
2.2 非保守力测量误差影响分析在星间距离变率测量误差和轨道误差分别为1 nm/s和1 mm的条件下, 分析当非保守力误差为3×10-9 m/s2、3×10-10 m/s2、3×10-11 m/s2和3×10-12 m/s2时对重力场反演精度的影响。获得4组地球重力场模型, 与标准模型比较后得到4组重力场模型误差, 将其表示为大地水准面阶误差, 见图 2。统计相应的大地水准面累积误差和重力异常累积误差, 结果见表 3。
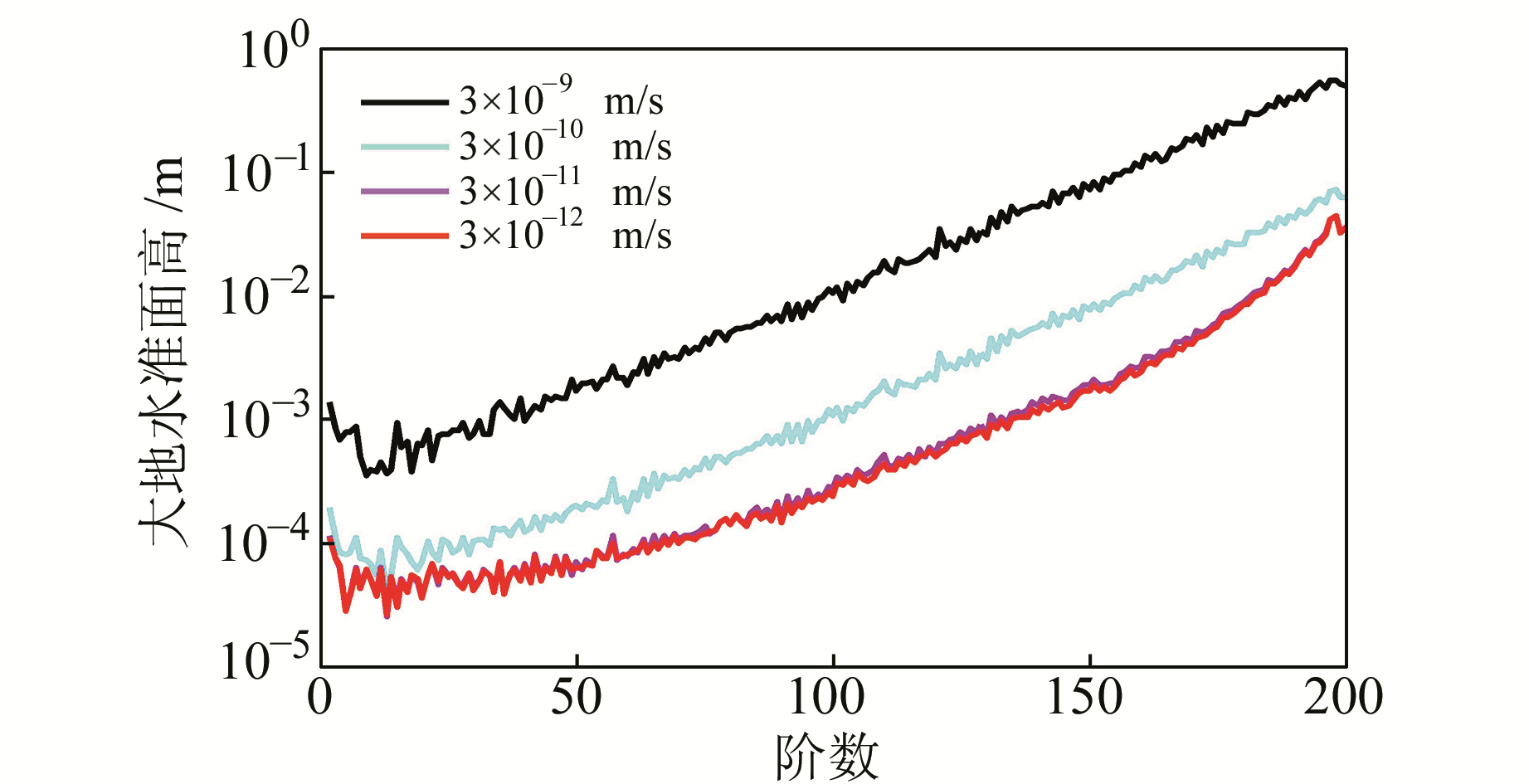
|
图 2 大地水准面阶误差 Fig. 2 The degree error of geoid |
|
|
表 3 非保守力误差对重力场精度的影响分析 Tab. 3 The effect on the accuracy of the gravity model from accelerometer error |
分析上述结果可知, 随着非保守力误差的减小, 重力异常和大地水准面误差均在减小。当非保守力误差达到3×10-11 m/s2水平时, 重力场反演的精度提高不再显著。因此, 非保守力测量精度控制在1~5×10-11m/s2量级即可满足高精度重力场测量的需求。
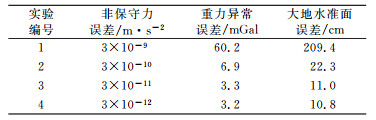
2.3 轨道测量误差影响分析在星间距离变率测量误差和非保守力误差分别为1 nm/s和1×10-12 m/s2的条件下, 分析轨道测量误差为5 cm、2 cm、5 mm和1 mm时对重力场恢复精度的影响。反演获得了4组地球重力场模型, 与基准重力场模型比较得到4组反演模型的误差, 表示为大地水准面阶误差, 见图 3。其重力异常累积误差和大地水准面累积误差统计见表 4。
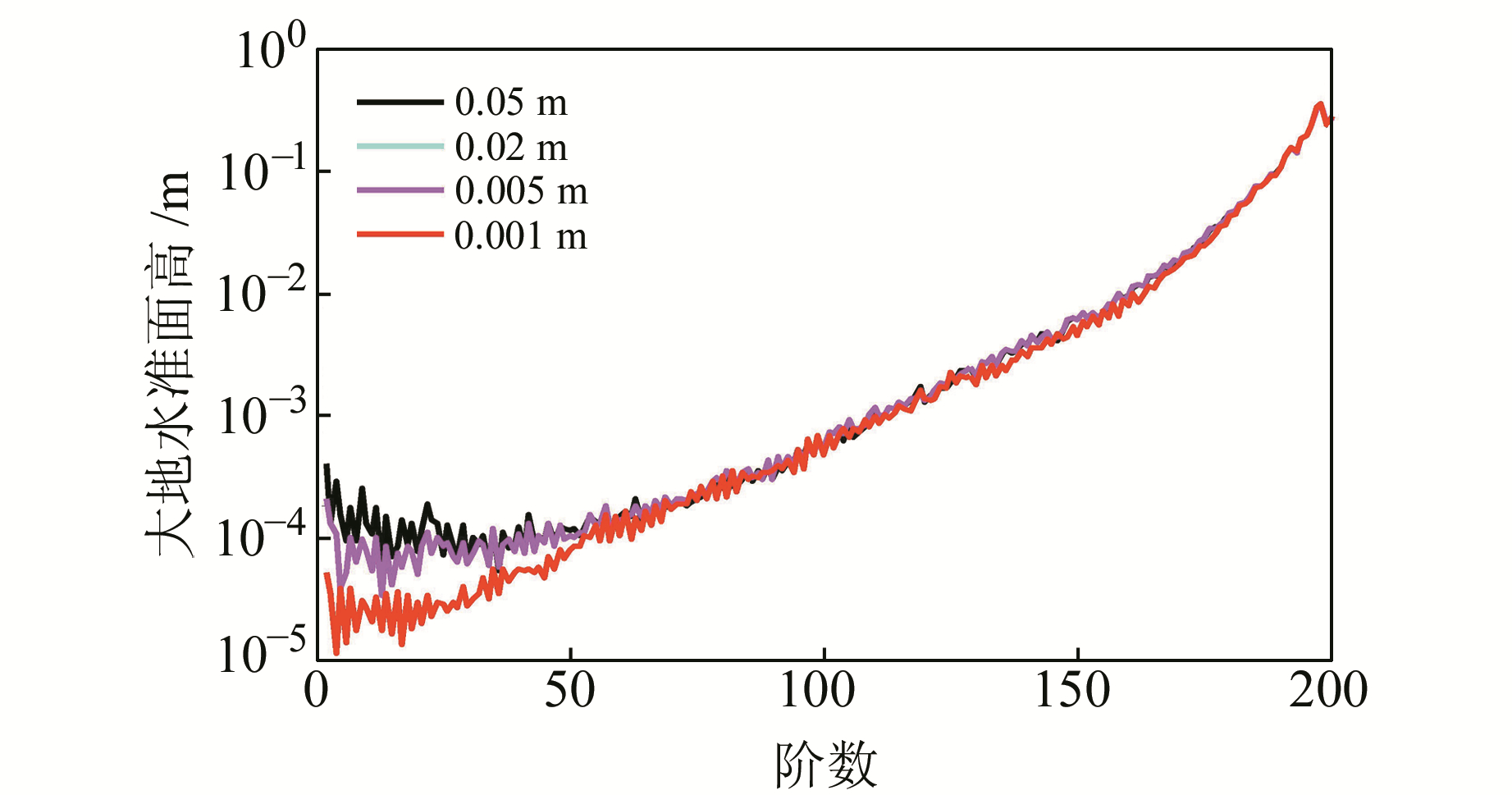
|
图 3 大地水准面阶误差 Fig. 3 The degree error of geoid |
|
|
表 4 轨道误差对重力场精度的影响分析 Tab. 4 The effect on the accuracy of the gravity model from orbit error |
由图 3可见, 轨道误差减小有利于低阶重力场恢复。由表 4可见, 轨道误差减小对重力场反演结果的整体影响并不显著, 2~5 cm轨道误差即可满足重力场反演的要求。综上可知, 重力卫星定轨精度提高有利于低阶重力场恢复, 可显著提高长波长(大于400 km)重力场求解精度。但是, 即使定轨精度提高到mm级, 对于中波(160~400 km)重力场信号恢复而言其误差量级仍然太大, 不足以显著改善此频段的重力场。中波重力场恢复主要依赖于星间距离变率测量值。
2.4 综合误差影响分析采用仿真方法分析各项载荷误差对重力场精度的综合影响。
实验1的载荷设计指标见表 5。
|
|
表 5 载荷设计指标 Tab. 5 The index design for all payloads |
按表 5条件仿真观测数据, 处理后获得1组地球重力场模型。将该模型与基准重力场模型比较, 获得反演模型的误差, 表示为大地水准面阶误差和累积误差, 结果见图 4(图中绿色曲线代表累积误差, 红色曲线代表阶误差)。

|
图 4 大地水准面阶误差与累积误差 Fig. 4 The degree error and accumulate error of geoid |
实验2的载荷设计指标见表 6。
|
|
表 6 载荷设计指标 Tab. 6 The index design for all payloads |
按实验2条件仿真观测数据, 处理后得到另1组地球重力场模型。将该模型与基准地球重力场模型比较, 得到反演模型的误差, 表示为大地水准面阶误差和累积误差, 结果见图 5(图中绿色曲线代表累积误差, 红色曲线代表阶误差)。

|
图 5 大地水准面阶误差与累积误差 Fig. 5 The degree error and accumulate error of geoid |
2项实验的累积误差统计结果见表 7(为阐述新一代重力卫星与类GRACE卫星指标关系, 将类GRACE卫星指标仿真结果也列入表 7最后一行)。
|
|
表 7 指标仿真结果 Tab. 7 The simulation results |
分析上述结果可知, 在实验1和实验2的误差配置条件下, 其精度均较类GRACE卫星指标提高了2~3倍。实验1和实验2的结果相当, 但进一步考虑到实用性和研制难度, 实验2的配置是较优选择。
3 结语综合分析各项实验结果, 并结合新一代重力卫星测量能力和载荷生产能力, 新一代低低卫星跟踪测量的核心技术指标体系设计为:在卫星轨道高度为300 km的条件下, 星间距离变率测量、非保守力测量、轨道确定的误差分别为10~30 nm/s、1~5×10-11 m/s2和2~5 cm。
新一代重力测量卫星将以100 km的分辨率、精度1~2 mGal的测量能力精确探测全球重力场, 成为获取全球重力场数据重要的技术手段, 较上一代重力测量卫星可获得更高频率的重力场信息, 弥补全球重力场测量技术的短板。
| [1] |
沈云中.应用CHAMP卫星星历精化地球重力场模型的研究[D].武汉: 中国科学院测量与地球物理研究所, 2000 (Shen Yunzhong. Study of Recovering Gravitational Potential Model from the Ephemerides of CHAMP[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2000)
(  0) 0) |
| [2] |
周旭华.卫星重力及其应用研究[D].武汉: 中国科学院测量与地球物理研究所, 2005 (Zhou Xuhua. Study on Satellite Gravity and Its Application[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2005) http://www.cnki.com.cn/Article/CJFDTotal-DXKJ200501000.htm
(  0) 0) |
| [3] |
徐天河.利用CHAMP卫星轨道和加速度计数据推求地球重力场模型[D].郑州: 信息工程大学, 2004 (Xu Tianhe. Gravity Field Recovery from Orbit and Accelerometer Data[D]. Zhengzhou: Information Engineering University, 2004)
(  0) 0) |
| [4] |
王正涛.卫星跟踪卫星确定地球重力场的理论与方法[D].武汉: 武汉大学, 2005 (Wang Zhengtao. Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Wuhan: Wuhan University, 2005) http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031869.htm
(  0) 0) |
| [5] |
肖云.基于卫星跟踪卫星数据恢复地球重力场的研究[D].郑州: 信息工程大学, 2006 (Xiao Yun. Research on the Earth Gravity Field Recovery from Satellite-to-Satellite Tracking Data[D]. Zhengzhou: Information Engineering University, 2006)
(  0) 0) |
| [6] |
张兴福.应用低轨卫星跟踪数据反演地球重力场模型[D].上海: 同济大学, 2007 (Zhang Xingfu. The Earth's Field Model Recovery on the Basis of Satellite-to-Satellite Tracking Missions[D]. Shanghai: Tongji University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10247-2007222863.htm
(  0) 0) |
| [7] |
肖云, 夏哲仁, 王兴涛. 用GRACE星间速度恢复地球重力场[J]. 测绘学报, 2007, 36(1): 19-25 (Xiao Yun, Xia Zheren, Wang Xingtao. Recovering the Earth Gravity Field from Inter-Satellite Range-Rate of GRACE[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 19-25 DOI:10.3321/j.issn:1001-1595.2007.01.004)
(  0) 0) |
| [8] |
陈秋杰, 沈云中, 张兴福. 基于重力卫星几何轨道线性化的地球重力场反演方法[J]. 地球物理学报, 2013, 56(7): 2238-2244 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu. Linearization Method of Recovering Earth's Gravity Field with Respect to Gravity Satellite's Kinematic Orbits[J]. Chinese Journal of Geophysics, 2013, 56(7): 2238-2244)
(  0) 0) |
| [9] |
Chen Q J, Shen Y Z, Zhang X F, et al. Global Earth's Gravity Field Solution with GRACE Orbit and Range Measurements Using Modified Short Arc Approach[J]. Acta Geodaetica et Geophysica, 2014, 50(2): 173-185
(  0) 0) |
| [10] |
Chen Q J, Shen Y Z, Zhang X F, et al. Monthly Gravity Field Models Derived from GRACE Level 1B Data Using a Modified Short Arc Approach[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(3): 1804-1819 DOI:10.1002/2014JB011470
(  0) 0) |
| [11] |
罗佳. 利用LEO星群反演地球重力场低阶带谐项变化的交叠点法[J]. 测绘学报, 2012, 41(5): 703-708 (Luo Jia. A Crossover Approach to Calculate the Time-Variable of the Earth Gravity Field Low Degree Zonal Harmonic Terms Based on LEO Cluster[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 703-708)
(  0) 0) |
| [12] |
宁津生, 钟波, 罗志才, 等. 基于卫星加速度恢复地球重力场的去相关滤波法[J]. 测绘学报, 2010, 39(4): 331-337 (Ning Jinsheng, Zhong Bo, Luo Zhicai, et al. Decorrelation Filtering Methods for Gravity Field Recovery Based on Satellite Acceleration Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 331-337)
(  0) 0) |
| [13] |
万晓云, 于锦海. 基地空白对GOCE引力场恢复的影响[J]. 测绘学报, 2013, 42(3): 317-322 (Wan Xiaoyun, Yu Jinhai. Influence of Polar Gaps on Gravity Field Recovery Using GOCE Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 317-322)
(  0) 0) |
| [14] |
邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641 (Zou Xiancai, Li Jiancheng, Wang Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641)
(  0) 0) |
| [15] |
周浩, 罗志才, 钟波, 等. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法[J]. 测绘学报, 2015, 44(8): 833-839 (Zhou Hao, Luo Zhicai, Zhong Bo, et al. MPI Parallel Algorithm in Satellite Gravity Field Inversion on the Basis of Least Square Method[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 833-839)
(  0) 0) |
| [16] |
庞振兴, 姬剑锋, 肖云, 等. 利用谱分析法估计GRACE Follow on地球重力场的空间分辨率[J]. 测绘学报, 2012, 41(3): 333-338 (Pang Zhenxing, Ji Jianfeng, Xiao Yun, et al. Estemation of the Resolution of Earth's Gravity Field for GRACE Follow on Using the Spectrum Method[J]. Acta Geodaeticaet Gartographica Sinica, 2012, 41(3): 333-338)
(  0) 0) |
| [17] |
姜卫平, 章传银, 李建成. 重力卫星主要有效载荷指标分析与确定[J]. 武汉大学学报:信息科学版, 2003, 28(增1): 104-109 (Jiang Weiping, Zhang Chuanyin, Li Jiancheng. Analysis and Determination of the Major Payload Indexes for Gravity Exploring Satellite[J]. Geomatics and Information Science of Wuhan University, 2003, 28(Supp1): 104-109)
(  0) 0) |
| [18] |
钟波.基于GOCE卫星重力测量技术确定地球重力场的研究[D].武汉: 武汉大学, 2010 (Zhong Bo. Study on Determination of the Earth's Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan: Wuhan University, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10486-2010167102.htm
(  0) 0) |
| [19] |
郑伟, 许厚泽, 钟敏, 等. 利用解析法有效快速估计将来GRACE Follow-On地球重力场的精度[J]. 地球物理学报, 2010, 53(4): 796-806 (Zheng Wei, Xu Houze, Zhong Min. Efficient and Rapid Estimation of the Accuracy of the Future GRACE Follow-On Earth's Gravitational Field Using the Analytic Method[J]. Chinese Journal of Geophysics, 2010, 53(4): 796-806 DOI:10.3969/j.issn.0001-5733.2010.04.004)
(  0) 0) |
| [20] |
郑伟, 许厚泽, 钟敏, 等. 卫星跟踪卫星测量模式中关键载荷精度指标不同匹配关系论证[J]. 宇航学报, 2011, 32(3): 697-705 (Zheng Wei, Xu Houze, Zhong Min, et al. Demonstration on Different Matching Relationship of Accuracy Indexes of Key Payload in the Satellite-to-Satellite Tracking Mode[J]. Journal of Astronautics, 2011, 32(3): 697-705 DOI:10.3873/j.issn.1000-1328.2011.03.037)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2017, Vol. 37
2017, Vol. 37