文章信息
- 熊伟腾, 王云英, 范金娟, 肖淑华
- XIONG Wei-teng, WANG Yun-ying, FAN Jin-juan, XIAO Shu-hua
- 非定向有机玻璃拉伸断口形貌与拉伸温度相关性分析
- Correlation analysis between tensile fracture morphology and tensile temperature of non-oriented acrylic sheet
- 材料工程, 2020, 48(10): 96-104
- Journal of Materials Engineering, 2020, 48(10): 96-104.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000482
-
文章历史
- 收稿日期: 2019-05-24
- 修订日期: 2019-12-19
2. 中国航发北京航空材料研究院 失效分析中心, 北京 100095
2. Failure Analysis Center, AECC Beijing Institute of Aeronautical Materials, Beijing 100095, China
航空有机玻璃因其合成成分和加工工艺不同于普通有机玻璃,冲击强度、弯曲强度、拉伸强度等均高于普通有机玻璃,常用作飞机的风挡、机舱、舷窗、舱盖等部位。随着飞机的飞行要求不断提升,航空有机玻璃在飞行过程中由应力损伤而产生的事故时有发生,例如:川航飞机风挡玻璃破裂脱落事故及各起鸟撞风挡玻璃事故[1]。为了分析航空有机玻璃在飞行过程中受到的应力种类,优先考虑分析有机玻璃断口,因为断口形貌能够客观真实地反映失效过程,肖淑华等[2]在分析飞机座舱盖玻璃开裂原因时,采用观察断口宏、微观形貌的方式,判断裂纹产生的性质,并通过力学实验综合分析开裂方式为疲劳开裂,即现阶段大部分的断口分析还停留在定性分析阶段,断口上大部分断裂信息容易被忽略[3],所以对航空有机玻璃断口深入探究,能够为航空有机玻璃的失效机理提供理论依据,对航空有机玻璃及非金属失效分析有着重要意义。
近年来很多学者对有机玻璃断口形貌的形成规律进行研究,并对有机玻璃的断裂机理及断口形成机理进行了探究。在断口形貌分析方面,对非定向有机玻璃进行静拉伸,利用扫描电镜观察其断口形貌特征,分析各特征区域形貌形成的原因; 王泓等[4]提出了有机玻璃裂尖微纤化断裂模型,并采用断裂力学方法对有机玻璃银纹微纤化的断裂机理进行了分析; 杨佳等[5]把不同牌号的有机玻璃断裂韧性和断口形貌进行联系,发现无论何种牌号的有机玻璃,断裂韧性和断面形貌都有一定的对应关系; Lach等[6]对有机玻璃单边缺口试样加载混合应力载荷,探究有机玻璃断口形貌与其加载应力之间的关系,并提出现阶段需要多采用断口形貌评估在混合加载条件下确切断裂行为的观点。另外,不少学者为了探究有机玻璃断裂机理,采用计算机模拟和摄影监控等方式对有机玻璃断裂过程进行分析,麻鸳鸳[7]通过高速摄影装置对有机玻璃的偏心裂纹动态传播的弯曲现象进行了记录并对现象进行了理论分析,定量分析了偏心距离和载荷幅值对裂纹动态传播行为的影响,得出了有机玻璃裂纹低速传播时,断面平滑,消耗的表面能量很低,而裂纹高速传播后,主裂纹断面粗糙,消耗的能量较多。Jiao等[8]通过设计不同宽度的开槽试样、未开槽试样等几种有机玻璃试样的拉伸实验,对有机玻璃的宏观分叉现象进行了系统的研究,实验结果表明传统的临界应力强度准则不适用于预测有机玻璃的宏观分叉现象,通过实验明确了有机玻璃的断裂特征,对有机玻璃的断裂机理提出了新的解释。
目前断口的定量分析方法包括:分形[9]、尺寸[10-11]、表面粗糙度的方法[12-14],例如:陶春虎等[15]介绍了临界裂纹长度和瞬断区面积来确定疲劳应力的工程运用及疲劳间距反推疲劳应力的基本原理,提出利用疲劳条带宽度反推疲劳应力,即通过断口的尺寸参数联系疲劳应力达到断口定量分析的目的,并利用该方法对直升机中减速轮、涡轮叶片、压气机叶片等金属材料断口进行分析; 于斌[16]通过对金属断口剖面轮廓线粗糙度和表面粗糙度进行测量,通过统计分析建立之间的关系,从而得到整体或局部断口的表面积,进而达到断口重建和定量测量的目的; 梁基照等[17]构建颗粒填充高分子复合材料拉伸断口的分形模型并提出了断口的分形维数与颗粒体积分数的理论关系式。而目前尚未发现有机玻璃断口形貌测算及标定方法方面的报道,故本研究尝试采用已有的断口定量分析方法,对不同拉伸温度下的非定向有机玻璃断口进行分析,进而对有机玻璃拉伸断口形貌变化规律和断裂机理进行探究。
本研究以牌号为YB-2的航空有机玻璃拉伸断口为研究对象,统计并分析其特征尺寸和表面粗糙度与拉伸温度之间的变化规律,并尝试基于分形理论采用分形维数对有机玻璃断口特征区域进行定量描述,通过分析三种变化规律,综合探究有机玻璃的断裂机理以及有机玻璃断口形貌定量研究的方法。
1 实验材料与方法 1.1 原料及拉伸实验实验原料为YB-2航空有机玻璃板材,厚度约5 mm,表面无明显划痕,依据GB/T 1040-2006,采用机械加工的方法制得有机玻璃拉伸试样。
利用INSTRON 5982电子万能试验机测量试样的拉伸应力,拉伸速率为1 mm·min-1,拉伸温度为实验变量,分别为-55,-20,0,23,60 ℃。
1.2 拉伸断口形貌观察及测量利用LEICA DMS 1000体视显微镜对有机玻璃拉伸断口进行观察,并测量有机玻璃拉伸断口特征区域的尺寸。非定向有机玻璃拉伸断口特征区域的宏观形貌差异较大:镜面区平整且高度反光; 雾状区平整但不反光,呈现出一定的粗糙度; 肋状区可见弧形的肋状条纹,并可见灰白色的撕裂层形貌。本研究通过断口各特征区域的形貌差异对其进行划分,并测量其区域长度,测量方法定义:起源位置到镜面区末端长度为镜面区长度l1,起源位置到雾状区末端长度为l2,镜面区末端到雾状区末端的绝对长度为雾状区长度l3(l3=l2-l1),断口各特征区域形貌和其测量方法见图 1。

|
图 1 有机玻璃断口宏观形貌 Fig. 1 Fracture macroscopic morphology of acrylic sheet |
利用LEXT OLS4100三维激光扫描仪观察有机玻璃三维断口形貌,并利用软件测量断口表面粗糙程度,采用轮廓算术平均偏差表示断口特征区域的粗糙程度,测量标准为GB/T 10610-2009。依据标准可知,被测物体的粗糙程度越高,对应的取样长度越长。而通过断口形貌观察可知,肋状区测量的表面粗糙程度较高,有较多起伏的肋边; 雾状区的微观形貌呈现有一定的粗糙度,与机械磨抛痕迹近似,并且由LEXT测量得出断口肋状区高差起伏较大,最大高差大于65 μm,而断口雾状区的高度起伏不大,最大高差约为10 μm。断口肋状区的高差起伏较大,结合标准中图解法估算断口肋状区需采用的取样长度为2.5 mm,评定长度为12.5 mm,而三维激光扫描仪的最小放大倍数为108倍,标准所需的取样长度超出了三维激光扫描仪能够拍摄范围; 断口雾状区高差起伏较小,选用三维激光扫描仪的放大倍数为432,粗糙度取样长度为0.8 mm,评定长度为4 mm,截止值(从横截面曲线中被除去的规定波长)为8 mm,在此条件下测量得出的表面粗糙度测量结果较为准确,所以本研究仅对断口雾状区进行测算及分析。
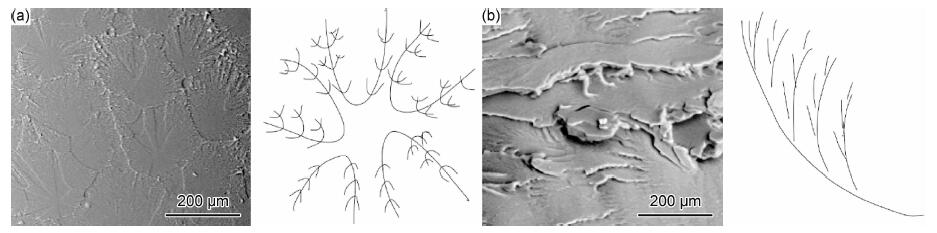
通过众多断口分形维数计算方法[18-20]可知,测量材料断口的分形维数首先需要确认材料断口属于随机分形图像,其次选择合适的断口分形特征提取方法,最后选择合适的断口分形维数计算方法[21]。本研究通过对有机玻璃断口进行分形刻画可知,有机玻璃断口雾状区和肋状区存在分形形貌,属于随机分形图形,见图 2; 其次利用扫描电镜-盒维数法测算有机玻璃断口上特征区域的分形维数D,测量步骤为:先用NanoSEM450扫描电镜对有机玻璃拉伸断口进行观察并拍摄照片,观察前对试样进行切割和断口表面喷金处理,然后采用Photoshop对扫描电镜拍摄后的照片裁剪,最后通过Matlab对裁剪后的照片进行灰度-二值化-盒维数计算处理得出断口特征区域的分形维数。
|
图 2 特征花样及其示意图 (a)“礼花状”特征花样及其示意图; (b)“羽毛状”特征花样及其示意图 Fig. 2 Feature patterns and its schematic diagrams (a)"fireworks"pattern and its schematic diagram; (b) "feather" pattern and its schematic diagram |
对拉伸实验结果进行统计,得到的不同温度下有机玻璃拉伸应力、拉伸强度平均值、标准差结果见表 1。
| T/℃ | σ/GPa | σ/GPa | SD | ||||
| -55 | 108.32 | 109.45 | 109.12 | 115.71 | 110.02 | 110.52 | 2.964 |
| -20 | 98.29 | 96.01 | 90.50 | 95.77 | 95.95 | 95.30 | 2.878 |
| 0 | 73.32 | 70.80 | 71.31 | 75.06 | 69.82 | 72.06 | 2.108 |
| 23 | 68.94 | 65.77 | 68.57 | 68.94 | 68.95 | 68.23 | 1.387 |
| 60 | 43.81 | 44.05 | 43.53 | 43.80 | 43.76 | 43.79 | 0.185 |
由表 1可见,拉伸温度为-55 ℃时,有机玻璃的拉伸强度平均值及其拉伸强度的标准差都相对较高,分别为110.52 GPa和2.964 GPa; 拉伸温度为60 ℃时,有机玻璃的拉伸强度平均值及其拉伸强度的标准差都相对较低,分别为43.76 GPa和0.185 GPa。
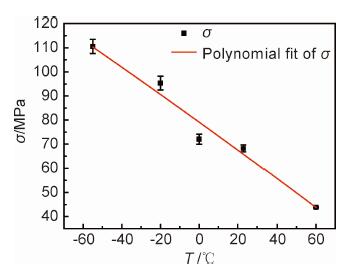
由表 1数据制得散点图,并曲线拟合,得出了T-σ拟合曲线,拟合度因子为0.942,温度-拉伸强度拟合曲线见图 3。
|
图 3 有机玻璃温度-拉伸强度拟合曲线及误差棒图 Fig. 3 Temperature-tensile strength fitting curve and error bar of acrylic sheet |
由图 3可知,随拉伸温度的提高,有机玻璃的拉伸强度降低,是因为随着拉伸温度的增加,分子链段上的各基团热运动变得活跃,尤其是有机玻璃的β松弛增加[22],分子链在外力和温度的共同作用下易于拉伸,并且裂尖银纹质变得柔软,裂纹顺着裂尖扩展容易,所以拉伸强度降低。由图 3还可以看出,随着拉伸温度的降低,拉伸强度偏差变大,即对应的拉伸强度标准差逐渐变大,说明拉伸温度越低,拉伸强度波动范围越大。
2.2 断口特征区域尺寸由于非定向有机玻璃在不同温度下拉伸后产生断口的特征区域大小不同[23],故本研究通过测量有机玻璃断口特征区域尺寸,探究断口形貌与拉伸温度之间的规律。有机玻璃不同起源位置的断口形貌如图 4所示,可见断裂一般为点源特征,并起源于试样边缘,镜面区形貌为平角扇形(图 4(a)),但是部分有机玻璃起源于有机玻璃棱边位置,镜面区形貌为直角扇环(图 4(b)),有机玻璃的镜面区和雾状区大小可能与起源位置有关,为了避免系统误差,取样时都选取了断裂起源于试样棱边位置的断口。

|
图 4 有机玻璃不同起源位置断口形貌 (a)平角扇形源区; (b)直角扇形源区 Fig. 4 Fracture morphologies of acrylic sheet at different origin position (a)flat angle fan source region; (b)right angle fan source region |
不同温度下的拉伸断口形貌如图 5所示,可见当拉伸速率相同,拉伸温度为-55 ℃时,有机玻璃断口表面的镜面区和雾状区较小,断口的绝大部分区域为肋状区,断口与试样工作段截面尺寸(约10.00 mm×4.85 mm)相近,断口尺寸大小为9.97 mm×4.72 mm,试样未产生明显的“细颈[24]”现象(图 5(a)); 当拉伸温度为60 ℃时,有机玻璃断口肋状区占整个断口的小部分,断口尺寸比试样工作段截面尺寸小,尺寸为9.86 mm×4.48 mm,横截面发生了明显变化,试样产生明显的“细颈”现象(图 5(b))。

|
图 5 不同温度下断裂的断口形貌对比 (a)-55 ℃; (b)60 ℃ Fig. 5 Comparison of fracture morphologies at different temperatures (a)-55 ℃; (b)60℃ |
对断口断裂特征区域的尺寸进行测量,将不同温度下的断口进行测量统计并计算其平均值,得出不同温度下的拉伸断口特征区域长度平均值l1,l2,l3分别见表 2。
| T/℃ | l1/mm | l2/mm | l3/mm |
| -55 | 0.193 | 1.450 | 1.257 |
| -20 | 0.383 | 1.953 | 1.570 |
| 0 | 0.544 | 2.851 | 2.307 |
| 23 | 0.663 | 3.538 | 2.875 |
| 60 | 0.814 | 5.792 | 4.978 |
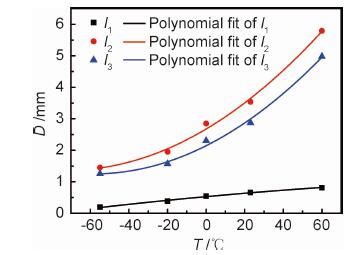
由表 2可见,拉伸温度由-55 ℃升高至60 ℃,l1,l2,l3均增大。由表 2数据制得散点图,并曲线拟合,得出了3条拉伸温度-长度拟合曲线,T-l1曲线拟合度因子为0.989,T-l2曲线拟合度因子为0.991,T-l3曲线拟合度因子为0.990,3条温度-长度拟合曲线见图 6。
|
图 6 特征区域尺寸拟合曲线 Fig. 6 Fitting curves of feature region size |
由图 6可知,随着拉伸温度的增加,l1,l2,l3均呈现为递增趋势,即镜面区和雾状区的尺寸随拉伸温度增加而增加,并且断口上镜面区和雾状区的形貌都近似为半圆形,所以镜面区和雾状区的面积随拉伸温度增加而增大。这是因为有机玻璃在相同拉伸速率的低温条件下,大分子链被高度冻结[24],裂尖银纹中的银纹质坚硬,不易被拉伸断裂,由于拉伸速率恒定,扩展时需要大部分能量维持裂纹的扩展,导致拉伸应力大幅增加,主裂纹的单个银纹则需通过多个银纹传递应力,使得主裂纹在扩展了较小区域后变为多个次级裂纹,则断口形貌上呈现为镜面区面积较小; 随着拉伸应力的持续增加,裂尖能量已超过裂纹扩展所需的能量,众多次级裂纹向多个平面扩展,形成了断口肋状形貌,由于拉伸应力增幅较大,导致断口雾状区面积较小。
2.3 断口表面粗糙度通过三维激光扫描仪测量得出有机玻璃断口雾状区轮廓算术平均偏差Ra,测量结果见表 3。
| T/℃ | Ra/μm | Ra/μm | ||||
| -55 | 0.458 | 0.454 | 0.563 | 0.570 | 0.541 | 0.517 |
| -20 | 0.422 | 0.449 | 0.478 | 0.483 | 0.382 | 0.443 |
| 0 | 0.419 | 0.422 | 0.397 | 0.426 | 0.390 | 0.411 |
| 23 | 0.354 | 0.345 | 0.337 | 0.345 | 0.331 | 0.342 |
| 60 | 0.344 | 0.331 | 0.323 | 0.326 | 0.325 | 0.330 |
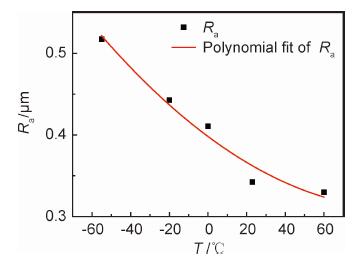
通过表 3可以得出,拉伸温度由-55 ℃升高至60 ℃,Ra下降幅度为36.17%;由表 3数据制得散点图,并曲线拟合,得出了T-Ra拟合曲线,拟合度因子为0.946,曲线见图 7。
|
图 7 雾状区 Ra 拟合曲线 Fig. 7 Fitting curve ofRa in foggy region |
由图 7可知,有机玻璃在相同的拉伸速率下,拉伸温度越高,断口雾状区的轮廓算术平均偏差值越小,即断口雾状区形貌越平滑。分析原因为:当有机玻璃在低温状态下拉伸,裂尖银纹质较坚硬,随着拉伸应力增大,裂尖微纤在较大的裂尖角度下发生断裂且轻微回弹,则在断口雾状区上形成了一定高度差的菊花状花样,即低温拉伸断口的雾状区形貌粗糙; 同理有机玻璃拉伸温度越高,裂尖银纹质较软,拉伸应力增幅较小,裂尖微纤在较小裂尖角度下便发生断裂,在断口雾状区形成高度差较小、较规律的礼花状花样,即高温下拉伸断口的雾状区形貌光滑。有机玻璃分别在-55,60 ℃下拉伸断裂后断口雾状区(喷金过后)三维形貌见图 8。

|
图 8 LEXT观察的断口雾状区三维形貌 (a)-55 ℃; (b)60 ℃ Fig. 8 Three-dimensional morphologies of fracture foggy region taken by LEXT (a)-55 ℃; (b)60 ℃ |
利用扫描电镜-盒维数测算断口分形维数,测算过程为电镜照片裁截-灰度处理-二值化处理-盒维数计算,灰度处理后示意图、二值化处理后示意图如图 9所示。

|
图 9 编程过程示意图 (a)扫描电镜裁截图; (b)二值化处理图 Fig. 9 Schematic diagrams of programming process (a)cropped SEM photo; (b)binarization processed photo |
由测量的特征区域(雾状区)尺寸可以得出,断口雾状区面积随拉伸温度的增大而增大,若测量断口分形维数时采用同一放大倍数测量不同拉伸温度下的断口形貌,则会导致同样大小的拍摄区域所得到的花样信息量不同,例如扫描电镜放大倍数为400时,能够观察到-55 ℃时拉伸断口雾状区的绝大部分区域以及众多花样,而在同样放大倍数下观察60 ℃时拉伸断口雾状区,仅能观察到雾状区小部分区域以及个别花样,导致观察的分形形貌不完整,对分行维数测量结果影响越大,所以本研究采用裁截相近花样个数的裁截标准,对电镜拍摄的断口照片进行裁截,并对裁截后的照片进行分形计算,得出不同拉伸温度下有机玻璃断口雾状区分形维数,不同拉伸温度下(温度由低到高)对应的分形维数分别为:1.357,1.404,1.453,1.483,1.579。
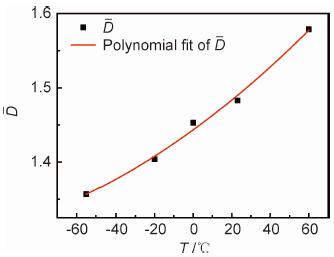
由对应的分形维数可得出:拉伸温度由-55 ℃升高到60 ℃,分形维数平均值持续增大,幅度为16.36%;由分形维数数据制得散点图,并曲线拟合,得出了T-D拟合曲线,拟合度因子为0.989,T-D拟合曲线见图 10。
|
图 10 温度-分形维数拟合曲线 Fig. 10 Temperature-fractal dimension fitting curve |
由图 10可知,当拉伸温度为-55 ℃时,有机玻璃断口雾状区的分形维数最小,当拉伸温度达到60 ℃时,有机玻璃断口雾状区的分形维数达到最大,并且T-D拟合曲线呈现出有机玻璃断口雾状区分形维数随拉伸温度升高而增大的变化规律。
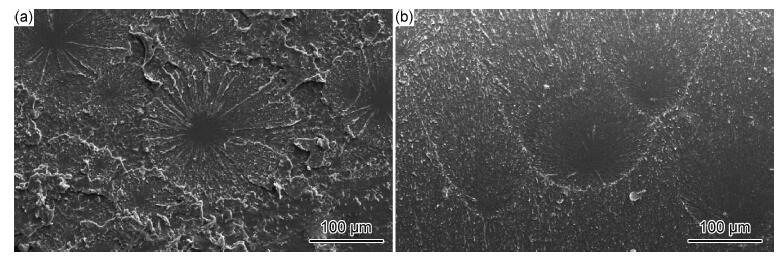
有机玻璃在低温状态下拉伸时,拉伸应力大幅增加,次级薄弱点激发形成银纹能够吸收能量,而大幅增加的拉伸应力产生的能量由大量激发的次薄弱点吸收,大量的次级薄弱点吸收能量后形成银纹并持续扩展,各银纹持续扩展形成次级裂纹,由于主裂纹和各次级裂纹还处于同一层面,各次级裂纹在扩展至交界位置停止并引发新的次级薄弱点,此断裂过程对应着断口雾状区,形貌呈现为菊花状花样数量较多、形貌尺寸较小、规则度高(图 11(a)),这便导致了低温拉断的断口雾状区分形维数值较低; 随着拉伸温度增加,拉伸应力增幅变小,材料内部的次薄弱点部分激发,断口雾状区形貌呈现为菊花状花样沿初始裂纹扩展方向偏向,花样数量较少、形貌尺寸较大,并且出现部分花样无规重叠的现象(图 11(b)),雾状区形貌规则度低,使得测算的分形维数值较高。
|
图 11 不同温度下雾状区形貌图 (a)-55 ℃; (b)60 ℃ Fig. 11 Morphologies of foggy region at different temperatures taken by SEM (a)-55 ℃; (b)60 ℃ |
通过动态模拟实验可知,当有机玻璃拉伸应力最大时,有机玻璃材料内部的微裂纹都处于拉伸状态,当应力再增加,超出了最大应力值时,有机玻璃最薄弱位置的微裂纹持续拉伸扩展为初级裂纹,即有机玻璃在拉伸强度开始下降时,微裂纹开始断裂并产生初始裂纹。
为了计算有机玻璃次级裂纹平面扩展(断裂形成雾状区)时所消耗的能量,本研究提出了两个假设。
假设1:有机玻璃在拉伸断裂时,拉伸强度短时间内未发生变化; 因为裂纹扩展的速率比较高,裂纹发生分叉时,裂纹的传播速率约为620 m·s-1[25],所以假设在断口断裂并形成镜面区的过程中,拉伸强度未发生改变。
假设2:有机玻璃次级裂纹平面扩展时(雾状区产生过程中),微裂纹的拉伸长度与其表面粗糙度Ra成正比关系α(α > 0);因为断口表面粗糙度Ra代表的是断口轮廓上各点高度在测量长度范围内的算术平均值,反映了物体表面峰谷的不平度,所以假定各银纹微纤的拉伸长度与其表面粗糙度成一定的正比关系。
通过假设1,可以推算断裂前雾状区对应区域中的单根银纹微纤的拉伸应力:
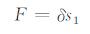
|
(1) |
式中:s1为单根银纹微纤初始拉伸时的截面积:δ为有机玻璃的拉伸强度。
通过假设2,可计算出单根银纹微纤拉伸断裂所消耗的能量:
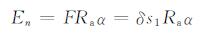
|
(2) |
式中:En为单根银纹微纤拉断时消耗的能量; Ra为断口表面粗糙度; α为关系系数。
若有机玻璃形成雾状区所拉断的微纤数量为n,那么机玻璃形成雾状区所消耗的能量为:
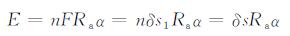
|
(3) |
式中:E为断口形成雾状区所消耗的能量; s为雾状区的面积。因为计算断口面积采用体式显微镜图片,断口都在相同倍数下观察,所以其雾状区面积s与图片的像素值γ成正比,并且β为一恒定正值,即s=βγ,即得出:
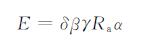
|
(4) |
所以,在两个假设的基础上,可通过推导公式对断口雾状区消耗能量进行比较,为了减少偶然误差,计算断口雾状区对应消耗能量公式中的δ,γ,Ra都以均值计算,得出各温度下的有机玻璃拉伸断口雾状区消耗能量结果,见表 4。
| T/℃ | Pixel mean value | E |
| -55 | 25425 | 1452755.01αβ |
| -20 | 39804 | 1680441.29αβ |
| 0 | 79169 | 2344721.36αβ |
| 23 | 140915 | 3288203.61αβ |
| 60 | 359135 | 5189752.14αβ |
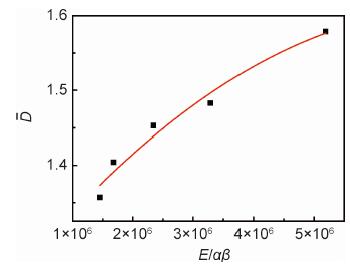
由表 4可得拉伸温度为-55 ℃时,断裂形成雾状区所消耗能量E为1452755.01αβ; 拉伸温度为60 ℃时,断裂形成雾状区所消耗能量E为5189752.14αβ。由表 4数据制得散点图,并曲线拟合,得出了ED拟合曲线,拟合度因子为0.942,ED拟合曲线见图 12。
|
图 12 能量-分形维数拟合曲线 Fig. 12 Energy-fractal dimension fitting curve |
由图 12可知,将不同温度下形成断口雾状区消耗的能量和其分形结果进行联系,随着拉伸温度的增加,形成断口雾状区的能量损耗越高,对应的形貌分形维数越大,即非定向有机玻璃断口雾状区的分形维数与其消耗能量成正相关关系。
3 结论(1) 在拉伸速率相同的情况下,有机玻璃断口特征区域尺寸、断口雾状区粗糙度、断口雾状区分形维数与拉伸温度的拟合曲线的拟合度因子都高于0.9,相关程度较高,即拉伸条件一致的情况下,能够采用形貌尺寸、粗糙度、分形维数对有机玻璃断口形貌定量分析,为有机玻璃断口定量分析研究奠定了一定的基础。
(2) 非定向有机玻璃断口雾状区的分形维数与其断裂时所消耗的能量成正相关关系。
| [1] |
邓小秋, 李志强, 赵隆茂, 等. 有机玻璃力学性能的研究现状[J]. 力学与实践, 2014, 36(5): 540-549. DENG X Q, LI Z Q, ZHAO L M, et al. A review on mechanical behaviour of PMMA[J]. Mechanics and Practice, 2014, 36(5): 540-549. |
| [2] |
肖淑华, 范金娟, 于爱珍. 飞机座舱盖玻璃开裂原因分析[J]. 材料开发与应用, 2018, 33(1): 72-76. XIAO S H, FAN J J, YU A Z. Analysis on the cause of cracks of an airplane canopy[J]. Material Development and Application, 2018, 33(1): 72-76. |
| [3] |
何玉怀, 姜涛, 刘新灵, 等. 失效分析[M]. 北京: 国防工业出版社, 2017: 5-6. HE Y H, JIANG T, LIU X L, et al. Failure analysis[M]. Beijing: National Defense Industry Press, 2017: 5-6. |
| [4] |
王泓, 鄢君辉, 郑修麟. 有机玻璃疲劳裂纹扩展定量分析[J]. 机械科学与技术, 2001, 20(1): 37-38. WANG H, YAN J H, ZHENG X L. The quantitative analysis on fatigue crack propagation of organic glass[J]. Mechanical Science and Technology, 2001, 20(1): 37-38. |
| [5] |
杨佳, 孙佳思, 郑飞, 等. 有机玻璃断裂韧性的断面形貌分析[J]. 玻璃, 2017(12): 36-38. YANG J, SUN J S, DENG F, et al. Analysis of section morphology for organic glass fracture toughness[J]. Glass, 2017(12): 36-38. |
| [6] |
LACH R, GRELLMANN W. Mixed mode fracture mechanics behaviour of PMMA[J]. Macromolecular Symposia, 2017, 373(1): 5-8. |
| [7] |
麻鸳鸳.脆性PMMA板动态断裂机理和裂纹传播形态研究[D].宁波: 宁波大学, 2014: 7-11. MA Y Y. Research on fracture mechanism and crack propagation form in brittle PMMA plates[D]. Ningbo: Ningbo University, 2014: 7-11. |
| [8] |
JIAO D, QU R T, ZHANG Z F. Macroscopic bifurcation and fracture mechanism of polymethyl methacrylate[J]. Advanced Engineering Materials, 2015, 17(10): 1454-1464. DOI:10.1002/adem.201500021 |
| [9] |
FU H, WANG W, CHEN X, et al. Fractal and multifractal analysis of fracture surfaces caused by hydrogen embrittlement in high-Mn twinning/transformation-induced plasticity steels[J]. Applied Surface Science, 2019, 470: 870-881. DOI:10.1016/j.apsusc.2018.11.179 |
| [10] |
于杰, 何敏, 刘一春, 等. 聚合物材料断面形貌特征定量分析[J]. 贵州科学, 2003, 21(1): 5-8. YU J, HE M, LIU Y C, et al. The quantitative analysis on fractured surface of polymer materials[J]. Guizhou Science, 2003, 21(1): 5-8. |
| [11] |
于斌, 靳庆臣. 金属断口宏观形貌几何特征定量测量及分析[J]. 有色金属工程, 2010, 62(3): 1-5. YU B, JIN Q C. Quantitative measurement and analysis of macroscopical morphology of fracture surface[J]. Nonferrous Metals Engineering, 2010, 62(3): 1-5. |
| [12] |
沈喆.应力集中与结构弛豫对Zr55Cu30Ni5Al10非晶合金弯曲断裂行为的影响[D].哈尔滨: 哈尔滨工业大学, 2016: 64-67. SHEN Z. Influence of stress concentration and structural relaxation on bending fracture behavior of a Zr55Cu30Ni5Al10 metallic glass[D]. Harbin: Harbin Institute of Technology, 2016: 64-67. |
| [13] |
冯新, 马英杰, 李建崇, 等. 铸造、锻造和粉末冶金TC4钛合金损伤容限行为对比研究[J]. 精密成形工程, 2018, 10(3): 46-54. FENG X, MA Y J, LI J C, et al. Comparative study on damage tolerance properties of TC4 titanium alloy manufactured by casting, forging and powder metallurgy[J]. Journal of Netshape Forming Engineering, 2018, 10(3): 46-54. |
| [14] |
李静, 朱知寿, 王新南, 等. 准β热处理工艺对TC4-DT钛合金裂纹扩展行为的影响[J]. 稀有金属, 2017, 41(7): 745-750. LI J, ZHU Z S, WANG X N, et al. Fatigue crack propagation behavior of TC4-DT alloy with quasi-β heat treatment[J]. Chinese Journal of Rare Metals, 2017, 41(7): 745-750. |
| [15] |
陶春虎, 习年生, 张卫方, 等. 断口反推疲劳应力的新进展[J]. 航空材料学报, 2000, 20(3): 158-163. TAO C H, XI N S, ZHANG W F, et al. Resent development of fractographic restrostimation on determining fatigue stress[J]. Journal of Aeronautical Materlals, 2000, 20(3): 158-163. |
| [16] |
于斌.金属断口的计算机三维重构及定量分析[D].兰州: 兰州理工大学, 2008: 60-65. YU B. Three-dimensional reconstruction and quantitative analysis of metallic fracture surface[D]. Lanzhou: Lanzhou University of Technology, 2008: 60-65. |
| [17] |
梁基照, 吴成宝. 颗粒填充高分子复合材料拉伸断口的分形模型[J]. 材料工程, 2008(1): 18-20. LIANG J Z, WU C B. Fractal model of tensile fracture for grain filled polymer composites[J]. Journal of Materials Engineering, 2008(1): 18-20. |
| [18] |
CARNEY L R, MECHOLSKY J J J. Relationship between fracture toughness and fracture surface fractal dimension in AISI 4340 steel[J]. Materials Sciences & Applications, 2013, 4(4): 258-267. |
| [19] |
齐菲.热冲击作用下多晶陶瓷微结构分形特征及损伤行为研究[D].哈尔滨: 哈尔滨工业大学, 2013: 10-11. QI F. Fractal characteristics of microstructure and damage behavior in polycrystalline ceramics under thermal shocks[D]. Harbin: Harbin Institute of Technology, 2013: 10-11. |
| [20] |
卢泽政, 李江腾. 岩状板岩断口分形与裂纹扩展速率研究[J]. 矿冶工程, 2017, 37(5): 15-18. LU Z Z, LI J T. Fracture fractal and crack propagation rate of layered slate[J]. Mining and Metallurgical Engineering, 2017, 37(5): 15-18. |
| [21] |
CHOI W, KIM J. Fractal dimensional analysis on glass fracture[J]. International Journal of Precision Engineering & Manufacturing, 2015, 16(7): 1655-1660. |
| [22] |
MARSHALL G P, COUTTS L H, WILLIAMS J G. Temperature effects in the fracture of PMMA[J]. Journal of Materials Science, 1974, 9(9): 1409-1419. DOI:10.1007/BF00552926 |
| [23] |
熊伟腾.基于分形理论的非定向有机玻璃拉伸断口形貌研究[D].南昌: 南昌航空大学, 2019: 24-26. XIONG W T. Study on tensile fracture morphology of non-oriented PMMA based on fractal theory[D]. Nanchang: Nanchang Hangkong University, 2019: 24-26. |
| [24] |
何平笙. 新编高聚物的结构与性能[M]. 北京: 科学出版社, 2009: 158-160. HE P S. Structure and properties of polymers[M]. Beijing: Science Press, 2009: 158-160. |
| [25] |
张振亚.脆性材料中动态裂纹传播问题的研究[D].宁波: 宁波大学, 2013: 40-48. ZHANG Z Y. Research on dynamic crack propagation in brittle materials[D]. Ningbo: Ningbo University, 2013: 40-48. |
 2020, Vol. 48
2020, Vol. 48


