文章信息
- 曹弘毅, 姜明顺, 马蒙源, 张法业, 张雷, 隋青美, 贾磊
- CAO Hong-yi, JIANG Ming-shun, MA Meng-yuan, ZHANG Fa-ye, ZHANG Lei, SUI Qing-mei, JIA Lei
- 复合材料层压板分层缺陷相控阵超声检测参数优化方法
- Parameter optimization method for delamination defects detection of composite laminate using phased array ultrasonic
- 材料工程, 2020, 48(9): 158-165
- Journal of Materials Engineering, 2020, 48(9): 158-165.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000777
-
文章历史
- 收稿日期: 2019-08-27
- 修订日期: 2019-09-18
相控阵超声技术是一种新型超声检测方法,由于其声束方向和聚焦深度灵活可控,可方便实现复杂结构件的全覆盖扫描。相比常规超声检测方法,具有高精度、高灵敏度、高检测效率等优势,因此在复合材料无损检测领域受到了越来越多的关注[1-3]。
相控阵超声声场是由各独立激发的单阵元声场叠加而成,其空间分布不仅受阵元尺寸、阵元间距等探头参数的影响,而且与聚焦法则和激活孔径紧密相关[4-5]。复合材料工艺结构特点对超声传播特性影响较大[6],此外相控阵超声叠加声场特性复杂,一定程度上影响了其在工程应用中的检测效果,需要建立声场模型对声场特性进行仿真分析,指导探头选型设计和检测参数优化,以保证检测结果的分辨力和准确性[7]。
相控阵超声声场建模方法有瑞利积分法[8-9]、多元高斯法[10-11]、有限元法[12-13]等,对于接触检测方式又存在界面条件下的声场建模问题。孙芳等[14]基于瑞利积分推导了双层介质条件下的相控阵声场模型,对安放在固体楔块上的相控阵阵列声场进行仿真分析,但其将固固界面简化为液固界面,影响了仿真结果的准确性。单宝华等[15]基于非近轴近似多元高斯模型推导出双层介质下的相控阵声场模型, 对横波检测相关模型进行了仿真分析,没有对纵波检测情况进行分析。Su等[16]利用有限元方法建立了相控阵超声在碳纤维增强树脂基复合材料(carbon fiber reinforced polymer, CFRP)中的传播模型,主要研究了其在复合材料中的声场聚焦特性;Lin等[17]利用有限元方法对阵元延时时间进行了校准,并对全聚焦成像算法进行修正,验证了其在复合材料缺陷检测方面的有效性。有限元法建模仿真结果准确,具有解决复杂问题的优势,但其全局离散的特性大大增加了其仿真时间。Wronkowicz等[18]对超声无损检测结果不确定度进行了研究,综合分析了影响检测效果的各种因素,但并未提出具体可行的优化方法。
本工作兼顾模型准确性与时效性,首先基于瑞利积分方法建立多点源三维声场模型,推导出固固界面下的相控阵超声声场模型;然后利用模型对相控阵零度聚焦扫查方法进行声场仿真,研究不同聚焦深度下激活孔径对声场特性的影响;最后根据仿真结果选择适当激活孔径对CFRP进行检测,实验结果表明,仿真优化后的激活孔径能够准确检测出预埋缺陷,检测精度较高。
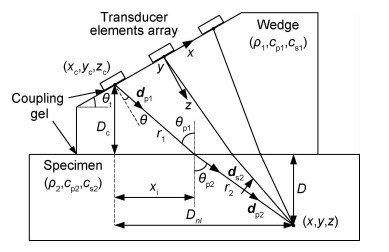
1 相控阵超声声场模拟相控阵超声用于接触式检测时,阵元声束经楔块进入被检试块,阵元与楔块、楔块与试块之间互相接触,其间涂抹一层很薄的液态耦合剂。相控阵超声通过电子方式控制各阵元激发和接收声波的延时时间来实现声束的偏转和聚焦,其检测声线如图 1所示,图中坐标原点为阵列中心位置。
|
图 1 相控阵超声检测声线辐射示意图 Fig. 1 Schematic diagram of acoustic radiation of phased array ultrasonic detection |
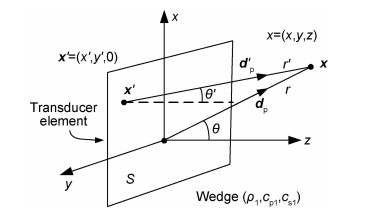
将单个阵元看作表面压强均匀的活塞式矩形阵元,设阵元面积为S、表面压强为p0(ω),其向楔块中辐射声波声线如图 2所示。
|
图 2 矩形阵元声线辐射示意图 Fig. 2 Schematic diagram of acoustic radiation of rectangular array |
用Rayleigh-Sommerfeld积分形式为高频弹性P波进行建模[19],其在楔块中产生的质点振动速度为:

|
(1) |
式中:kp1为波数; ω为角频率;ρ1, cp1分别为楔块密度和纵波波速;r为阵元形心到点x的距离; r′为点x′到点x的距离。Kp(θ′)为声场指向性函数,d′p为点x′到点x单位极化矢量。
为使用数值分析方法应用式(1),将长宽分别为lx, ly的矩形阵元在x方向R等分、在y方向Q等分,假设在分割面积很小的情况下r′≈r,基于高频近似和稳相法推导单个阵元在楔块中的多点源三维声场模型为:
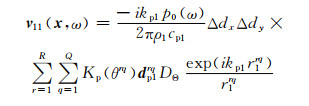
|
(2) |
式中:Δdx, Δdy分别为分割小阵元的长和宽;uxrq, uyrq分别为其在x, y方向的单位向量;DΘ为声束方向性系数,其表达式为:

|
为尽量避免因阵元分割大小产生的声场栅瓣,阵元分割数量必须满足以下条件[20]:
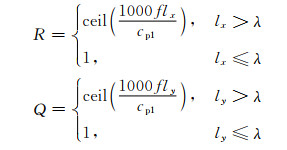
|
(3) |
式中:f为阵元中心频率;λ为波长。
楔块和被检试块之间存在液态耦合剂,界面处只传播纵波,声学边界条件满足光滑界面条件。根据声学边界条件理论及射线理论[20],推导出单阵元在试块中的多点源三维声场模型为:
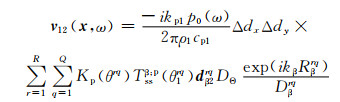
|
(4) |
式中: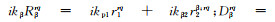
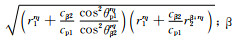
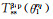
设相控阵阵列在x, y方向的阵元数量分别为N, L个,阵元长宽分别为lx, ly,阵元间隙宽度分别为gx, gy。相控阵超声聚焦法则的计算方法基于射线理论[21],根据声线几何关系与snell定律计算出阵元nl到聚焦点的传输时间为:
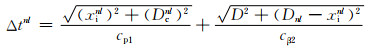
|
(5) |
式中:n, l分别表示阵元在x, y方向上的阵元序号(n=1, …, N; l=1, …L);xinl, Dnl分别为阵元nl形心到声线透射点和聚焦点的水平距离;Dcnl为阵元nl形心到界面处的垂直距离;D为聚焦深度。如图 1所示。
阵列中每个阵元的延时时间计算公式如下:
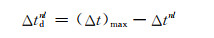
|
(6) |
式中:(Δt)max为阵列中阵元到聚焦点的最大传输时间。
根据惠更斯原理,对各阵元在楔块和试块中的声场进行叠加计算,并施加聚焦法则,得到相控阵阵列在楔块和试块中的总辐射声场模型分别为:
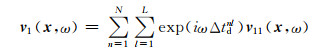
|
(7) |
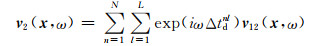
|
(8) |
式(5)中聚焦法则的计算与聚焦深度相关,而聚焦法则是相控阵超声聚焦和偏转的决定因素;由式(7), (8)可知,相控阵超声探头确定后,其激活孔径是唯一影响其叠加声场特性的参数,是影响检测成像分辨力的关键参数。
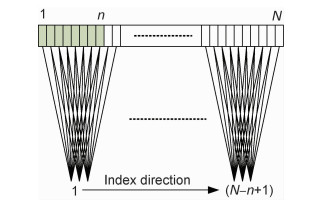
2 仿真分析使用相控阵超声对CFRP层压板进行检测时,声束垂直入射到平板内部时聚焦效果最好[22],应选择零度聚焦扫查方法对其检测。设一维线阵探头的阵元数为N 、阵元间距为d,当激活孔径为n、步进为1时,零度聚焦扫查示意图如图 3所示。其横向扫查有效范围为(N-n+1)d,当N,d确定后,扫查有效范围随着激活孔径 n的增大而减小。
|
图 3 零度聚焦扫查方法示意图 Fig. 3 Schematic diagram of zero-degree focus scanning method |
相控阵超声探头选择适用于复合材料检测的近壁探头,型号为5L64-NW1,其具有较小的阵元尺寸与阵元间距,探头参数如表 1所示。
| Frequency/MHz | Elementsnumber | x directionsize/mm | y directionsize/mm | Arraygap/mm |
| 5 | 64 | 0.9 | 7 | 0.1 |
楔块型号选择SNW1-0L,材质为有机玻璃,高度为20 mm。试块为CFRP层压板,使用东丽T300编织预浸料制备。楔块和试块的材料特性如表 2所示。
| Material | Density/(g·cm-3) | P-wave velocity/(m·s-1) | S-wave velocity/(m·s-1) |
| Plexiglass | 1.18 | 2730 | 1480 |
| CFRP | 1.54 | 3112 | 2088 |
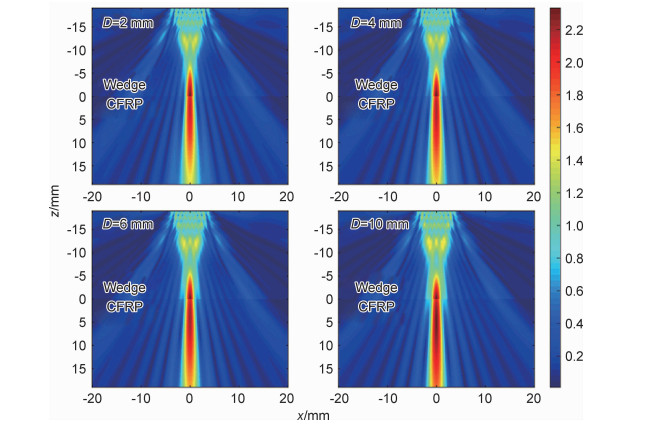
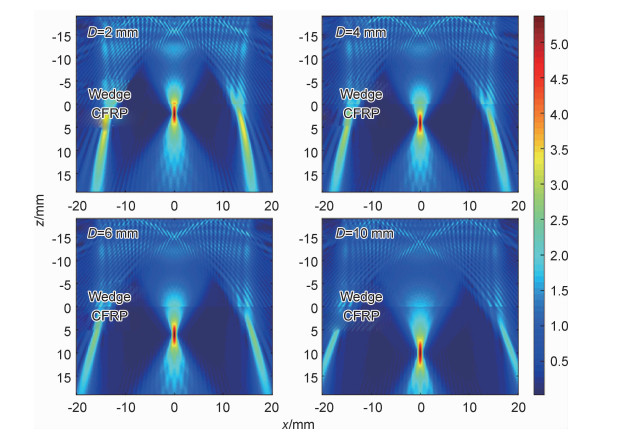
利用式(7),(8)建立的声场模型对y=0的xz平面内二维声场进行仿真,声场辐射空间范围设定为40 mm×40 mm,空间网格单元划分为0.1 mm×0.1 mm。不同激活孔径和聚焦深度组合下的声场仿真结果如图 4~6所示(声场质点速度幅值使用归一化幅值),图 4~6分别对应激活孔径n为8,16,32;每张图中4幅小图分别对应聚焦深度D为2,4,6,10 mm,图中z=0处为楔块与试块界面,界面以上部分为楔块中声场仿真图像,界面以下部分为试块中声场仿真图像。
|
图 4 n=8时声场仿真结果 Fig. 4 Simulation result of sound field when n=8 |

|
图 5 n=16时声场仿真结果 Fig. 5 Simulation result of sound field when n=16 |
|
图 6 n=32时声场仿真结果 Fig. 6 Simulation result of sound field when n=32 |
不同激活孔径下聚焦深度设定值与仿真值对比如图 7所示,可以看出,激活孔径越大聚焦深度仿真值与设定值误差越小,聚焦越准确。当激活孔径为8时,深度误差随着聚焦深度设定值的增大而增大,只在2 mm时能准确聚焦;当激活孔径为16和32时,聚焦深度设定值与仿真值基本一致。

|
图 7 不同激活孔径下聚焦深度仿真值 Fig. 7 Simulation focus depth at different activation apertures |
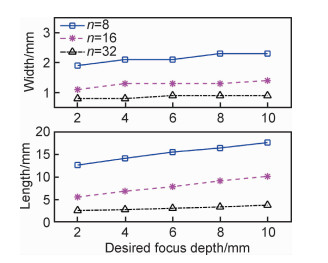
聚焦区域为声场中能量较高的区域,焦区长度为主声轴上焦点前后相对于焦点处声压下降20%的轴向长度,焦区宽度为焦点处声场横切面上相对于焦点处声压下降50%的横向长度[4]。不同激发孔径下各聚焦深度的聚焦声场焦区宽度和长度如图 8所示。
|
图 8 不同激活孔径下焦区范围 Fig. 8 Focal zone range at different activation apertures |
可以看出,同一聚焦深度下,焦区宽度和长度都会随着激活孔径的增大而不断减小,但变化幅度在降低;同一激活孔径下,焦区宽度基本保持不变,而焦区长度随着聚焦深度的增大而增大,并且激活孔径越大焦区长度变化幅度越小。激活孔径越大,其聚焦区域越小,声束指向性越好,横向分辨力越高。
2.3 主声轴幅值分析为定量分析焦区能量与激活孔径和聚焦深度的关系,提取主声轴(x=0)归一化幅值进行分析,幅值曲线如图 9所示。可以看出,主声轴幅值近距离处(< 10 mm)幅值持续振荡;在楔块与试块界面处(z=0)由于界面透射衰减而突降,然后在试块内部再逐渐聚焦增强,并在焦点处到达最大值后逐渐降低。

|
图 9 不同激活孔径下主声轴归一化幅值 (a)n=8;(b)n=16;(c)n=32 Fig. 9 Normalized amplitude of main axis at different activation apertures (a)n=8;(b)n=16;(c)n=32 |
当聚焦深度在0~10 mm范围内时,同一激活孔径下,不同聚焦深度时焦点处幅值基本一样;只有激活孔径为32时,焦点能量会随着聚焦深度增大而缓慢增大,因声场栅瓣能量泄漏减少,声场能量更为集中。
图 10为聚焦深度为2 mm时不同激活孔径下的主声轴幅值曲线,焦点幅值随着激活孔径的增加而增大,但增加幅度减小,激活孔径由16增加到32时幅值只增加了23.4%。激活孔径越大非聚焦区域声束衰减越严重,且固固界面处声场强度相比焦区小很多,不利于近表面处缺陷检测。

|
图 10 同一聚焦深度时不同激活孔径主声轴幅值图 Fig. 10 Main axis amplitude of different activation at the same focus depth |
综合上述分析,激活孔径越大声场聚焦效果越好,但非焦区声场严重发散,影响非焦区轴向检测结果准确性,降低系统检测效率;而且在聚焦深度较小情况下,激活孔径越大栅瓣能量越强,更容易产生伪像。因此,相控阵超声检测过程中,激活孔径并非越大越好。应针对试块厚度对激活孔径进行优化选择,提高检测分辨力,保证其检测结果的准确性与检测效率。
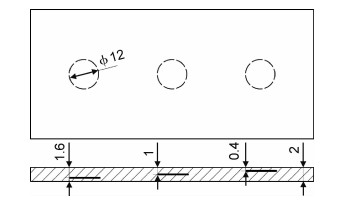
3 实验验证为进一步验证优化方法的可行性,设计制备含分层缺陷的CFRP层压板并对其进行相控阵超声检测。层压板采用热压工艺制备,制备压力0.6 MPa、最高温度130 ℃,材料为东丽T300编织预浸料,采用层叠铺层方式,层数为10层。其尺寸为150 mm×75 mm,内部不同深度埋入3个直径为12 mm的聚四氟乙烯薄膜制备分层缺陷,埋深约为1.6,1.0,0.4 mm,如图 11所示。
|
图 11 缺陷尺寸及分布示意图 Fig. 11 Schematic diagram of defect size and distribution |
相控阵主机为OmniScanMX2,探头和楔块与上述仿真时所选型号一致,使用编码器获取扫查过程中的行程位置。制备的CFRP层合板厚度约为2 mm,因此,对聚焦深度为2 mm时的声场仿真结果进行分析,综合聚焦区域范围及焦区能量,选择激活孔径为8对其进行检测。使用上述相控阵超声检测系统对CFRP层合板进行检测,并设置TCG(time controlled gain)增益增强反射信号强度,C扫描和B扫描图分别如图 12(a),(b)所示。
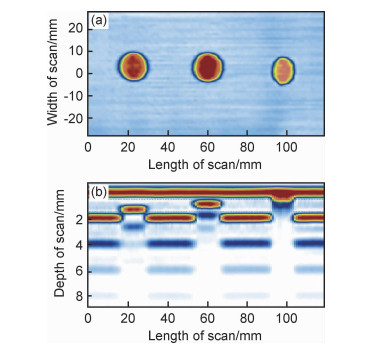
|
图 12 CFRP层压板相控阵检测图像 (a)C扫描;(b)B扫描 Fig. 12 Phased array detection image of CFRP laminate (a)C-scan; (b)B-scan |
图 12(a)中缺陷从左向右依次为近下表面、中间层、近上表面,由图可知,近下表面和中间层缺陷形状与实际缺陷形状相近,而近上表面缺陷由于近表面原因,检测效果不如前两处缺陷;图 12(b)能够很清晰地看到三处缺陷的不同埋深,近上表面处缺陷由于埋深太浅,其反射信号与CFRP上表面反射信号混叠。
分别采用-6 dB法和时差法计算检测图像中缺陷的尺寸与埋深,尺寸测量时使用矩形框圈定方法,缺陷埋深和尺寸误差计算结果如表 3所示。
| Location | Depth error/mm | Length error/mm | Width error/mm |
| Bottom | -0.35 | 0.20 | -0.15 |
| Middle | -0.17 | 0.30 | 0.25 |
| Top | 0.10 | -1.13 | -0.35 |
实验结果表明,除近上表面处缺陷由于近表面原因其长度测量误差较大,其他测量误差均 < 0.5 mm,检测误差较小,检测结果较准确,验证了模型仿真分析方法在激活孔径选择上的有效性。
4 结论(1) 针对相控阵超声接触式检测方法,基于瑞利积分推导的固固界面下的多点源三维声场模型能够准确、高效地对其声场进行仿真。
(2) 仿真结果表明,激活孔径是影响声场聚焦特性的关键因素,在不同聚焦深度下应该选择合适的激活孔径进行检测,以保证相控阵超声检测的准确性及高效性。
(3) 实验结果表明,针对不同厚度被检试块,利用仿真方法优化选取相控阵超声激活孔径,其分层缺陷检测结果比较准确,埋深与尺寸检测误差均较小,验证了声场仿真方法对激活孔径配置具有很好的指导作用,对无损检测定量评估具有重要意义。
| [1] |
周正干, 孙广开, 李洋. 先进无损检测技术在复合材料缺陷检测中的应用[J]. 航空制造技术, 2016, 59(4): 28-35. ZHOU Z G, SUN G K, LI Y. Application of advanced nondestructive testing technologies for the detection of defects in composites[J]. Aeronautical Manufacturing Technology, 2016, 59(4): 28-35. |
| [2] |
GHOLIZADEH S. A review of non-destructive testing methods of composite materials[J]. Procedia Structural Integrity, 2016, 1(1): 50-57. |
| [3] |
何方成, 王铮, 史丽军, 等. 复合材料制件拐角部位超声检测技术[J]. 材料工程, 2011(7): 80-84. HE F C, WANG Z, SHI L J, et al. Ultrasonic testing technique for the inspection of defects in the corner of composites[J]. Journal of Materials Engineering, 2011(7): 80-84. |
| [4] |
陈振华, 黄智刚, 王婵, 等. 超声相控阵检测声场的有限元仿真建模及其试验验证[J]. 电子测量与仪器学报, 2018, 32(2): 48-55. CHEN Z H, HUANG Z G, WANG C, et al. Finite element modulation and its experimental verification on sound field of ultrasonic phased array testing[J]. Journal of Electronic Measurement and Instrument, 2018, 32(2): 48-55. |
| [5] |
温姣玲, 卢超, 何方成, 等. 航空复合材料层压板钻孔分层缺陷相控阵检测参数优化[J]. 玻璃钢/复合材料, 2017, 1(2): 21-25. WEN J L, LU C, HE F C, et al. Research on optimal parameters of ultrasonic phased array detection of drilling-induced delamination in composite laminates[J]. Fiber Reinforced Plastics/Composites, 2017, 1(2): 21-25. |
| [6] |
王铮, 何方成, 梁菁, 等. 复合材料层板铺层方式对超声检测结果的影响[J]. 材料工程, 2013(2): 50-54. WANG Z, HE F C, LIANG J, et al. Influence of the orientation of laying-up in composite laminates on ultrasonic inspection[J]. Journal of Materials Engineering, 2013(2): 50-54. |
| [7] |
杨平华, 林莉, 刘春伟, 等. 相控阵超声检测横向分辨力实验测试及分析[J]. 仪器仪表学报, 2011, 32(6): 1384-1389. YANG P H, LIN L, LIU C W, et al. Experimental measurement and analysis of the lateral resolution of phased array ultrasonic detection[J]. Chinese Journal of Scientific Instrument, 2011, 32(6): 1384-1389. |
| [8] |
WANG T, ZHANG C, ALEKSOV A, et al. Two-dimensional analytic modeling of acoustic diffraction for ultrasonic beam steering by phased array transducers[J]. Ultrasonics, 2017, 76(Complete): 35-43. |
| [9] |
SONG S J, KIM C H. Simulation of 3-D radiation beam patterns propagated through a planar interface from ultrasonic phased array transducers[J]. Ultrasonics, 2002, 40: 519-524. DOI:10.1016/S0041-624X(02)00176-2 |
| [10] |
ZHAO X Y, GANG T. Nonparaxial multi-Gaussian beam models and measurement models for phased array transducers[J]. Ultrasonics, 2008, 49(1): 126-130. |
| [11] |
韩鹏, 王召巴, 陈友兴, 等. 多元高斯声束模型相控阵超声传感器声场仿真[J]. 传感器与微系统, 2010, 29(2): 22-25. HAN P, WANG Z B, CHEN Y X, et al. Simulation of sound fields of phased array ultrasonic sensor based on multi-Gaussian beam model[J]. Transducer and Microsystem Technologies, 2010, 29(2): 22-25. |
| [12] |
ITO J, BIWA S, HAYASHI T, et al. Ultrasonic wave propagation in the corner section of composite laminate structure:numerical simulations and experiments[J]. Composite Structures, 2015, 123(1): 78-87. |
| [13] |
XU N, ZHOU Z G. Numerical simulation and experiment for inspection of corner-shaped components using ultrasonic phased array[J]. NDT & E International, 2014, 63(1): 28-34. |
| [14] |
孙芳, 曾周末, 王晓媛, 等. 界面条件下线型超声相控阵声场特性研究[J]. 物理学报, 2011, 60(9): 1-6. SUN F, ZENG Z M, WANG X Y, et al. Acoustic field characteristics of ultrasonic linear phased array for an interface condition[J]. Acta Physica Sinica, 2011, 60(9): 1-6. |
| [15] |
单宝华, 李冬生, 郭佳, 等. 双层界面下非近轴近似多元高斯模型的相控阵声场模拟[J]. 声学学报, 2017, 42(4): 75-82. SHAN B H, LI D S, GUO J, et al. Radiation beam simulation of ultrasonic phased array based on a nonparaxial multi-Gaussian beam model with double interfaces[J]. Acta Acustica, 2017, 42(4): 75-82. |
| [16] |
SU H M, LUO Z B, CAO H Q, et al. Focal law design for phased array ultrasonic testing of CFRP based on finite element modeling[C]//2016 IEEE Far East NDT New Technology & Application Forum (FENDT). IEEE, 2016.
|
| [17] |
LIN L, CAO H Q, LUO Z B. Total focusing method imaging of multidirectional CFRP laminate with model-based time delay correction[J]. NDT & E International, 2018, 97(1): 51-58. |
| [18] |
WRONKOWICZ A, DRAGAN K, LIS K. Assessment of uncertainty in damage evaluation by ultrasonic testing of composite structures[J]. Composite Structures, 2018, 203(1): 71-84. |
| [19] |
SCHMERR JR L W. Fundamentals of ultrasonic nondestructive evaluation:a modeling approach[M]. New York: Plenum Press, 1998.
|
| [20] |
SCHMERR L W Jr. Fundamentals of ultrasonic phased arrays[M]. New York: Springer, 2014.
|
| [21] |
CERVENY V. Seismic ray theory[M]. Cambridge: Cambridge University Press, 2005.
|
| [22] |
徐娜, 沙正骁, 史亦韦. 超声相控阵延迟时间的声速校正及在复合材料中的检测[J]. 材料工程, 2015, 43(9): 74-79. XU N, SHA Z X, SHI Y W. Velocity correction of delay time and inspection for composite materials using ultrasonic phased array[J]. Journal of Materials Engineering, 2015, 43(9): 74-79. |
 2020, Vol. 48
2020, Vol. 48


