文章信息
- 陈子木, 胡正伟, 王倩妮, 史亦韦
- CHEN Zi-mu, HU Zheng-wei, WANG Qian-ni, SHI Yi-wei
- 薄壁结构工业CT尺寸测量误差与极限
- Error and limit determination for dimensional measurements of thin-walled structures with industrial computed tomography
- 材料工程, 2020, 48(8): 169-176
- Journal of Materials Engineering, 2020, 48(8): 169-176.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000286
-
文章历史
- 收稿日期: 2019-03-27
- 修订日期: 2020-05-12
2. 航空材料检测与评价北京市重点实验室, 北京 100095;
3. 中国航空发动机集团材料检测与评价重点实验室, 北京 100095
2. Beijing Key Laboratory of Aeronautical Materials Testing and Evaluation, Beijing 100095, China;
3. Key Laboratory of Aeronautical Materials Testing and Evaluation, Aero Engine Corporation of China, Beijing 100095, China
为了实现飞机结构减重、功能整合、性能提升的目标,以满足先进飞机的经济性、可靠性需求,复杂薄壁结构越来越多地应用于飞机零部件设计中,并且对制造工艺的要求也越来越高。增材制造技术,能够采用拓扑优化实现高性能复杂结构金属零件的无模具、快速、全致密近净成形,显著减轻结构质量,减少零件数量并提高可靠性,成为应对先进飞机制造技术挑战的有效途径,也为实现结构紧凑性和多功能设计创造了重要条件。然而,由于传统的接触式或光学式尺寸测量方法,其测点难以抵达内部结构表面,因此,难以满足增材制造复杂结构在尺寸方面成形质量的评价要求,在一定程度上限制了增材制造技术的推广应用[1-3]。
工业CT尺寸测量技术作为工业CT检测技术在无损检测领域中的具体应用之一,是一种非接触式坐标测量技术[4-6]。相对于传统的三坐标测量机,该技术的优势在于:可实现几何量的无损表征,同时具有内外表面的可达性;点云数据获取更加密集,可实现复杂结构快速成像[7-9]。因此,目前国内外正积极开展工业CT三维精密测量技术研究[10-12]。在工业CT尺寸测量应用研究方面,Kiekens等对影响工业CT系统测量值误差进行了研究[13],Van Bael等将工业CT应用于多孔结构几何形状控制,计算孔结构尺寸、壁厚、结构体积等几何信息,完成产品几何形状的控制[14]。在尺寸测量精度方面,GE公司通过红宝石球进行验证实验,并采用散射线补偿的方法提高测量精度,最高可达(4+L/100) μm。在测量标准方面,德国《VDI/VDE 2630工业CT尺寸测量》系列标准,包含了原理与术语、测量影响因素与建议、尺寸测量应用指南、测量过程及比较、测量不确定度等方面。国内工业CT技术主要应用于无损检测领域,在几何量测量和计量化应用方面起步较晚。工业CT测量技术的需求主要来源于产品尺寸检验,王义旭等针对工业CT探测尺寸误差进行了校准和分析[15]。在国内公开的标准方面,涉及工业CT结构尺寸测量的相关标准仅有GB/T 29067-2012 《无损检测工业计算机层析成像(CT)图像测量方法》。目前可参考的国内外文献及标准,鲜有针对小尺寸薄壁结构的测量误差进行特别说明。
作为增材制造典型结构之一的薄壁结构,其厚度可小至不足1 mm。工业CT系统由于其系统性能约束,对于薄壁结构边界已不可明显分辨,因此限制了薄壁结构壁厚测量的准确性。本工作首先讨论了薄壁结构CT成像规律,在此基础上推导了薄壁结构边界在像空间的位置,比较半高宽法和最大灰度梯度法两种边界确定方法的适用范围,并利用CT系统性能确定基于CT成像的可测壁厚尺寸极限,最后通过经计量校准的薄壁标准件CT检测实验结合理论计算模拟灰度分布曲线,验证不同厚度薄壁结构的测量误差。
1 薄壁结构CT成像的灰度分布薄壁结构可视为线状物体沿其法线方向的连续有限分布,设法线方向平行于x轴的薄壁壁厚为x0,当薄壁结构为均质材料时,其在一维物空间中可通过式(1)表示。
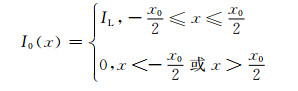
|
(1) |
式中:IL为材料在物空间中的强度;I0(x)为结构在物空间中的强度分布函数。工业CT成像系统是一类典型的线性平移不变系统,如果将该成像系统的线扩散函数(line spread function, LSF)写成一维形式,记作L(x),则L(x)表征了CT成像系统对线状物体成像的基本特性,任意位置x1处的线状物体IL(x1),经过工业CT成像后得到的像函数I(x)可用式(2)表示。
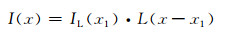
|
(2) |
对于厚度为x0且在物空间坐标系中关于x=0对称的连续均匀薄壁结构,经过工业CT系统成像后,可视为多个线状物体成像的线性叠加,因此其分布可写成如式(3)的积分的形式。
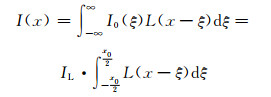
|
(3) |
由于线扩散函数L(x)关于x=0具有轴对称性的特征,容易得到L(x)=L(-x),将式(3)改写为式(4)的形式:
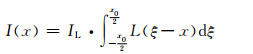
|
(4) |
令ξ-x=η,且再次利用L(x)的轴对称性转换积分区间可得到薄壁结构在像空间中的分布函数,见式(5)。

|
(5) |
可以看出,在像空间中任意一点x处的像强度I(x),等于线扩散函数在该位置两侧各
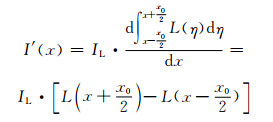
|
(6) |
因此,一旦CT成像系统的线扩散函数L(x)确定,就可以通过计算模拟的方法得到不同厚度薄壁结构经过成像系统后的灰度分布及灰度梯度分布。
2 薄壁结构边界在像空间中的位置薄壁结构尺寸测量是基于结构经成像系统成像后的图像坐标进行测量,因此在得到薄壁结构成像规律后,还需要确定其边界在像空间中对应的特征位置,以表征其在物空间中的尺寸。为了简化后续讨论,不妨假设CT成像系统的线扩展函数L(x)为有限展宽,即:
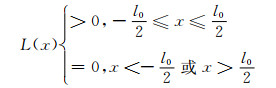
|
(7) |
其中l0为线扩散函数的扩展宽度。对于大多数工业CT成像系统,其线扩散函数都能在有限范围内衰减为0,因此该假设具有普适性。根据式(5),薄壁结构边界处灰度可用式(8)表示为:
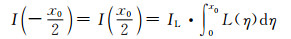
|
(8) |
此时边界处灰度梯度的绝对值为:
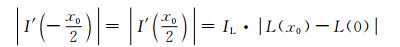
|
(9) |
对于某一固定的成像系统,线扩展函数L(x)的扩展宽度l0为定值。
(1) 当壁厚x0≥l0时
通过式(5)可知,在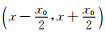
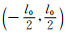
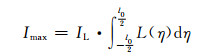
|
(10) |
此时边界处灰度可通过式(11)计算。
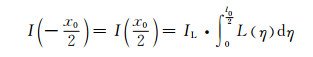
|
(11) |
因此有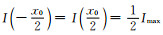
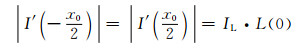
|
(12) |
由线扩散函数的非负性L(x)≥0可得,对于图像上任意一点的梯度绝对值有|I′(x)|≤IL·(Lmax-Lmin),其中Lmax=L(0)且Lmin=0,因此|I′(x)|≤IL·L(0),故此时边界处为图像灰度分布的最大梯度位置。
(2) 当壁厚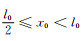
由于壁厚尺寸小于线扩散函数扩展宽度且线扩散函数随着远离坐标原点单调递减,因此在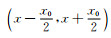
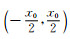
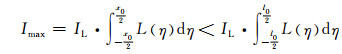
|
(13) |
此时边界处灰度依然为:
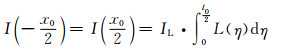
|
(14) |
边界处灰度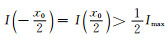
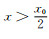

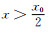
而此时依然有L(x0)=0,薄壁结构边界在像空间中的灰度梯度绝对值可表示为:
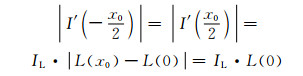
|
(15) |
对于图像上任意一点梯度同样有|I′(x)|≤IL·(Lmax-Lmin)=IL·L(0),所以此时薄壁结构边界处仍然为灰度梯度绝对值最大的位置。
(3) 当壁厚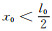
类似的,此时薄壁结构在像空间中的最大灰度可表示为:

|
(16) |
而薄壁结构边界处灰度为:
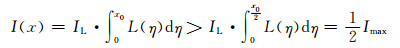
|
(17) |
可以得知,此时边界灰度同样大于最大灰度的1/2。且当x>0时,L(x)单调递减至0,因此随着x增大,由于积分区间长度一定,I(x)=IL· 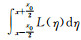
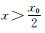
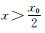
此时边界位置处的灰度梯度绝对值为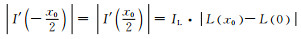

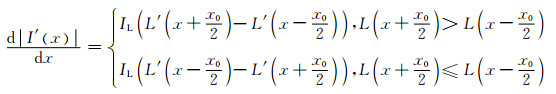
|
(18) |
当
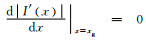
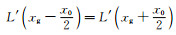
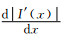
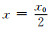

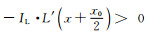
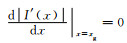
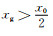
从上述推导可知,当壁厚尺寸x0 < l0时,采用半高宽法表征薄壁结构边界位置开始产生明显偏差;而当x0 < l02时,采用最大梯度法表征薄壁结构边界位置也开始产生明显偏差。为了评估不同边界表征方法引入的壁厚测量误差大小,现展开如下讨论:
(1) 半高宽法
当x0 < l0时,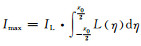
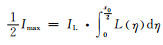
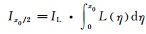
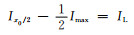
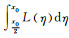
当
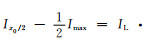
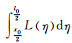
当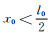

当x0→0,半高宽法对应的测量极限可用式(19)表示。
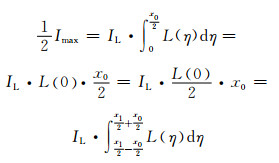
|
(19) |
其中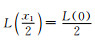
(2) 最大灰度梯度法
对于最大灰度梯度法,可以采用类似的分析,但由于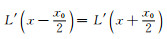
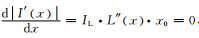
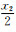
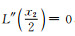
综上所述,可以得到:
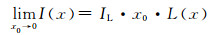
|
(20) |
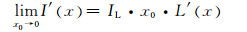
|
(21) |
可以看出,随着壁厚逐渐减小,其像灰度分布趋近于线扩散函数的分布,其像灰度梯度分布趋近于线扩散函数的梯度分布。因此,半高宽法和最大灰度梯度法对于薄壁结构的测量极限,是线扩散函数的半高间距和最大梯度的间距,任何测量值不会小于该值。由此可知,当薄壁结构壁厚尺寸小于该极限时,测量误差随尺寸减小显著增大,该极限值表征了成像系统的最小壁厚测量能力,因此称为可测壁厚尺寸极限。
4 薄壁结构工业CT尺寸测量实验通常情况下,一个成像系统的线扩散函数难以通过实验直接获得,但其边扩散函数(edge spread function, ESF) 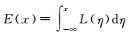
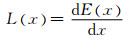
|
(22) |
对厚度经校准的薄壁结构进行工业CT扫描成像,选用GE Phoenix v|tome|x C450工业CT成像系统,实验参数为:管电压400 kV,管电流1500 μA,积分时间100 ms,放大比2,探测器一次微动,像素尺寸0.1 mm,不使用滤波片,探测器通过空气进行校准,试样旋转一周采集1000幅图像。对于扫描参数和试样摆放固定的工业CT系统,才可视为成像规律固定的一套成像系统,其线扩散函数可用于表征该成像系统的成像性能。薄壁结构试样及其专用工装如图 1所示,为保证试样厚度为对比实验中的唯一变量,选择专用工装固定在工业CT转台上并保证试样厚度方向平行于CT旋转平面。

|
图 1 厚度经校准的薄壁结构试样(a)及工装(b) Fig. 1 Thin-walled structure samples (a) with thickness calibrated and fixture tools (b) |
选择厚度分别为4.00, 3.50, 3.00, 2.50, 2.00, 1.50, 1.00, 0.75, 0.50 mm的薄壁结构,相同厚度的试样数量为3个,其校准厚度偏差小于±0.35 μm。
对于厚度小于0.50 mm的薄壁结构,则选择厚度分别为0.40, 0.30, 0.20 mm的塞尺进行工业CT扫描成像并测量厚度。对于所有厚度的薄壁结构,工业CT成像系统的测量误差远大于真实值相对于标称值的偏差,因此标称值可视为真实值作为判断该成像系统尺寸测量误差的对比参考。
对薄壁结构进行工业CT扫描成像,结果如图 2所示。

|
图 2 不同壁厚薄壁结构工业CT成像 (a)4.00 mm; (b)3.50 mm; (c)3.00 mm; (d)2.50 mm; (e)2.00 mm; (f)1.50 mm; (g)1.00 mm; (h)0.75 mm; (i)0.50 mm; (j)0.40 mm; (k)0.30 mm; (l)0.20 mm Fig. 2 Industrial CT images of the thin-walled structures with different thicknesses (a)4.00 mm; (b)3.50 mm; (c)3.00 mm; (d)2.50 mm; (e)2.00 mm; (f)1.50 mm; (g)1.00 mm; (h)0.75 mm; (i)0.50 mm; (j)0.40 mm; (k)0.30 mm; (l)0.20 mm |
对每个薄壁结构沿壁厚方向做灰度分布分析,不同厚度的薄壁结构灰度分布经幅值归一化后如图 3所示。可以看出,厚度小于0.50 mm的薄壁结构灰度分布都接近于厚度为0.50 mm的薄壁结构。
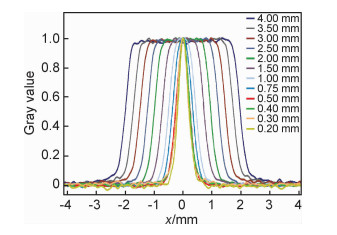
|
图 3 不同厚度薄壁结构图像实验测量灰度分布 Fig. 3 Gray value distribution of the thin-walled structures with different thicknesses measured by experiment |
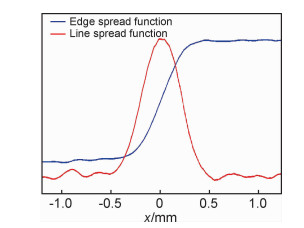
为了解释该现象,对4.00 mm薄壁结构边扩散函数求导可得当前工业CT成像系统的线扩散函数,如图 4所示。
|
图 4 工业CT成像系统的边扩散函数及线扩散函数 Fig. 4 Edge spread function and line spread function of industrial CT imaging system |
利用式(5)和实际测量的线扩散函数,可以计算出不同厚度薄壁结构理论灰度分布,归一化的灰度分布曲线如图 5所示。对于厚度等于0.50 mm的薄壁结构,其扩展宽度已经与线扩散函数扩展宽度一致,即0.50 mm厚度的薄壁结构已经趋近于成像系统的尺寸测量极限,因此小于0.50 mm的薄壁结构经成像系统成像,其归一化的灰度分布曲线都趋近于线扩散函数分布。

|
图 5 不同厚度薄壁结构图像理论计算灰度分布 Fig. 5 Gray value distribution of the thin-walled structures with different thicknesses calculated |
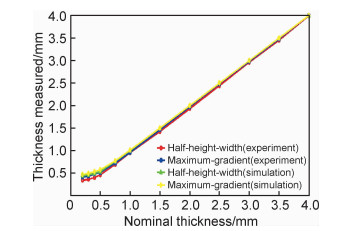
为了进一步验证半高宽法和最大灰度梯度法对不同厚度薄壁结构的测量误差,分别通过理论计算以及实验测量的图像灰度分布进行尺寸分析,得到的壁厚测量结果如表 1和图 6所示。可以看出对于理论计算的薄壁结构灰度分布,当壁厚尺寸大于线扩散函数扩展宽度时,半高宽法和最大梯度法的测量误差均小于±0.01 mm;当壁厚尺寸小于线扩散函数扩展宽度但大于壁厚测量极限值时,最大灰度梯度法具有更小的测量误差;当壁厚尺寸小于壁厚测量极限时,测量误差显著增大,随着薄壁结构厚度减小,半高宽法和最大梯度法的壁厚测量值均趋近于壁厚测量极限,这也与上述的解析分析相一致。但对于实验测量的壁厚尺寸,当实际壁厚大于壁厚测量极限值时,半高宽法相比最大灰度梯度法一直具有更小的测量误差,对于本工作采用的工业CT成像系统,半高宽法尺寸测量误差小于±0.04 mm,最大灰度梯度法尺寸测量误差小于±0.08 mm,这主要是由于灰度梯度的计算较灰度极值更为灵敏,因此受系统噪声影响明显。随着薄壁结构尺寸减小至小于壁厚测量极限,半高宽法和最大灰度梯度法尺寸实验测量结果依然呈单调下降的趋势,测量误差显著增大,但此时最大灰度梯度法的测量误差相比半高宽法较小。随着薄壁结构厚度减小,成像调制度下降导致受系统噪声的影响程度大幅增加,采用半高宽法和最大灰度梯度法计算壁厚均会产生严重的误差,因此与理论推导的结果产生较大偏差。对比实验测量结果和理论计算结果发现,当薄壁结构尺寸大于壁厚测量极限时,两者具有较好的一致性,当薄壁结构尺寸小于壁厚测量极限时,理论计算结果趋近于某个固定值。虽然实验测量结果依然能够保持尺寸减小的趋势,但是测量误差逐渐增大。
| No | Nominal thickness |
Experimental result | Simulation result | |||
| Half- height- width |
Maximum- gradient |
Half- height- width |
Maximum- gradient |
|||
| 1 | 4.00 | 4.00 | 3.99 | 4.00 | 4.00 | |
| 2 | 3.50 | 3.48 | 3.45 | 3.50 | 3.50 | |
| 3 | 3.00 | 2.98 | 2.96 | 3.00 | 3.00 | |
| 4 | 2.50 | 2.48 | 2.44 | 2.50 | 2.50 | |
| 5 | 2.00 | 1.97 | 1.93 | 2.00 | 2.00 | |
| 6 | 1.50 | 1.46 | 1.42 | 1.50 | 1.50 | |
| 7 | 1.00 | 0.96 | 0.95 | 1.01 | 1.00 | |
| 8 | 0.75 | 0.72 | 0.69 | 0.77 | 0.76 | |
| 9 | 0.50 | 0.51 | 0.46 | 0.57 | 0.53 | |
| 10 | 0.40 | 0.48 | 0.40 | 0.53 | 0.49 | |
| 11 | 0.30 | 0.43 | 0.36 | 0.49 | 0.46 | |
| 12 | 0.20 | 0.41 | 0.34 | 0.47 | 0.44 | |
|
图 6 薄壁结构壁厚测量结果对比 Fig. 6 Comparison of the thin-walled structure thicknesses measured |
(1) 当薄壁结构尺寸大于线扩散函数扩展宽度时,半高宽法和最大灰度梯度法均能准确表征结构边界;当薄壁结构尺寸小于线扩散函数扩展宽度但大于其宽度1/2时,最大灰度梯度法能够准确表征结构边界而半高宽法存在一定误差;当薄壁结构尺寸小于线扩散函数扩展宽度1/2时,最大灰度梯度和半高宽法均不能准确表征结构边界且测量结果偏大。
(2) 随着薄壁结构尺寸减小,其像灰度分布趋近于线扩散函数的分布,半高宽法和最大灰度梯度法对于薄壁结构的测量极限,分别是线扩散函数的半高间距和最大梯度的间距,该极限表征了CT成像系统的最小壁厚尺寸测量能力。
(3) 由实验测量和理论结果对比可知,两者具有较好的一致性;但当薄壁结构尺寸大于可测壁厚尺寸极限时,最大灰度梯度法测量结果受成像系统噪声影响较大,最终实验结果显示半高宽法相比最大灰度梯度法具有更小的测量误差。当薄壁结构尺寸小于可测壁厚尺寸极限时,两种表面确定方法由系统噪声引起的实验测量误差均显著增大。
(4) 成像系统的测量极限可以通过实验测量边扩散函数分布利用计算模拟的方法获得。
| [1] |
凌松. 增材制造技术及其制品的无损检测进展[J]. 无损检测, 2016, 38(6): 60-64. LING S. Additive manufacture technique and related NDT for its products[J]. Nondestructive Testing, 2016, 38(6): 60-64. |
| [2] |
杨平华, 高祥熙, 梁菁, 等. 金属增材制造技术发展动向及无损检测研究进展[J]. 材料工程, 2017, 45(9): 13-21. YANG P H, GAO X X, LIANG J, et al. Development tread and NDT progress of metal additive manufacture technique[J]. Journal of Materials Engineering, 2017, 45(9): 13-21. |
| [3] |
张学军, 唐思熠, 肇恒跃, 等. 3D打印技术研究现状和关键技术[J]. 材料工程, 2016, 44(2): 122-128. ZHANG X J, TANG S Y, ZHAO H Y, et al. Research status and key technologies of 3D printing[J]. Journal of Materials Engineering, 2016, 44(2): 122-128. |
| [4] |
THOMPSON A, MASKERY I, LEACH R K. X-ray computed tomography for additive manufacturing:a review[J]. Measurement Science & Technology, 2016, 27(7): 072001. |
| [5] |
NTIVEROS S, YAGUE J A, JIMENEZ R, et al. Computer tomography 3D edge detection comparative for metrology applications[J]. Procedia Engineering, 2013, 63: 710-719. DOI:10.1016/j.proeng.2013.08.263 |
| [6] |
MULLER P, CANTATORE A, ANDREASEN J L, et al. Computed tomography as a tool for tolerance verification of industrial parts[J]. Procedia CIRP, 2013, 10: 125-132. DOI:10.1016/j.procir.2013.08.022 |
| [7] |
MAIRE E, WITHERS P J. Quantitative X-ray tomography[J]. International Materials Reviews, 2017, 59(1): 1-43. |
| [8] |
DE CHIFFRE L, CARMIGNATO S, KRUTH J P, et al. Industrial applications of computed tomography[J]. CIRP Annals-Manufacturing Technology, 2014, 63(2): 655-677. |
| [9] |
ALOISI V, CARMIGNATO S. Influence of surface roughness on X-ray computed tomography dimensional measurements of additive manufactured parts[J]. Case Studies in Nondestructive Testing and Evaluation, 2016, 6: 104-110. DOI:10.1016/j.csndt.2016.05.005 |
| [10] |
TAN Y, KIEKENS K, WELKENHUYZEN F, et al. Simulation-aided investigation of beam hardening induced errors in CT dimensional metrology[J]. Measurement Science & Technology, 2014, 25(6): 064014. |
| [11] |
ANTONDU P, STEPHAN G R, JOHAN E, et al. Application of micro CT to the non-destructive testing of an additive manufactured titanium component[J]. Case Studies in Nondestructive Testing & Evaluation, 2015, 4: 1-7. |
| [12] |
TOWNSEND A, PAGANI L, SCOTT P, et al. Areal surface texture data extraction from X-ray computed tomography reconstructions of metal additively manufactured parts[J]. Precision Engineering, 2017, 48: 254-264. DOI:10.1016/j.precisioneng.2016.12.008 |
| [13] |
DEWULF W, KIEKENS K, TAN Y, et al. Uncertainty determination and quantification for dimensional measurements with industrial computed tomography[J]. CIRP Annals-Manufacturing Technology, 2013, 62(1): 535-538. |
| [14] |
VAN BAEL S, KERCKHOFS G, MOESEN M, et al. Micro-CT-based improvement of geometrical and mechanical controllability of selective laser melted Ti6Al4V porous structures[J]. Materials Science and Engineering:A, 2011, 528(24): 7423-7431. DOI:10.1016/j.msea.2011.06.045 |
| [15] |
王义旭, 施玉书, 高思田, 等. 工业CT探测尺寸误差的校准及误差分析[J]. 计量学报, 2014, 35(3): 216-220. WANG Y X, SHI Y S, GAO S T, et al. Calibration and analysis for probing size error of industrial CT[J]. Acta Metrologica Sinica, 2014, 35(3): 216-220. DOI:10.3969/j.issn.1000-1158.2014.03.05 |
 2020, Vol. 48
2020, Vol. 48


