文章信息
- 陈利, 焦伟, 王心淼, 刘俊岭
- CHEN Li, JIAO Wei, WANG Xin-miao, LIU Jun-ling
- 三维机织复合材料力学性能研究进展
- Research progress on mechanical properties of 3D woven composites
- 材料工程, 2020, 48(8): 62-72
- Journal of Materials Engineering, 2020, 48(8): 62-72.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000210
-
文章历史
- 收稿日期: 2020-03-12
- 修订日期: 2020-04-29
2. 天津工业大学 纺织科学与工程学院, 天津 300387
2. College of Textile Science and Engineering, Tiangong University, Tianjin 300387, China
三维纺织复合材料具有多样化的预制体结构、大范围可调节的纤维取向和纤维含量,可以实现材料性能的裁剪设计,同时,厚度方向纤维的引入使其具有优良的层间性能,已在航空航天、交通运输、海洋船舶等工程领域得到了广泛应用[1]。
三维机织预制体是三维纺织复合材料中应用最为广泛的增强体结构,其生产效率高、可设计性强,且具有优异的复杂结构近净成型能力[2]。Chen等[3]对三维机织预制体结构和制备方法进行了全面评述。近年来,采用三维机织结构增强的高性能复合材料得到了迅速的发展。研究人员对三维机织复合材料的典型力学性能进行了全面深入的研究,取得了显著成果,并开展了三维机织复合材料的冲击、疲劳等动态力学性能的研究表征[4-6]。Hallal[7]和Ansar等[8]对三维机织复合材料的力学性能预报模型进行了综述。Gereke等[9]总结了主要的三维机织预制体的建模方法。
本文介绍了三维机织复合材料预制体的结构类型和特点,综述了碳纤维3D角联锁机织复合材料的最新力学性能研究进展以及三维机织复合材料数值建模方法,列举了三维机织复合材料在航空航天领域的应用实例,提出了三维机织复合材料工程应用中需要进一步解决的关键问题。
1 三维机织预制体结构三维机织预制体是利用多层经纱织造方法,将若干层经纱和纬纱接结在一起而形成的三维整体预制体[4]。典型的三维机织预制体包含两个纱线系统,即接结经纱系统和纬纱系统,沿织物成型方向排列的接结经纱系统通过弯曲穿过若干层纬纱层并将伸直的纬纱捆绑在一起,形成一个整体不分层的三维结构。表 1列出了三维机织预制体分类情况。典型的三维机织预制体结构按接结经纱贯穿纬纱层的方式可分为直联机织结构和角联机织结构;按照接结经纱的运动规律可分为平纹结构、斜纹结构和缎纹结构。在典型的三维机织预制体结构中可以引入伸直的衬经纱系统,形成包含3个纱线系统的预制体结构,其最简单结构为正交三向结构,该结构中贯穿厚度的接结经纱将伸直的衬经纱和纬纱捆绑在一起,且3个纱线系统相互垂直。在角联机织结构中引入伸直的衬经纱系统形成衬经角联机织结构,可以显著增强材料的经向性能。近年来,为了提高三维机织复合材料面内抗剪切性能,含斜向纱线的多轴向三维机织预制体的制备技术得到迅速发展。张一帆等[10]描述了两种多轴向三维织物预制体的制备新工艺,其一为在正交三向织物成型工艺的基础上,通过特殊的斜向携纱机构引入斜向纱线;其二为铺纱置换法制备多轴向多层织物。Bilisik[11]综述了多轴向机织技术的发展;Labanieh等[12]对比分析了多轴向三维机织技术中斜向纱的引入方式,开发了导块式斜向纱引入技术。陈利等[13]在层联机织结构基础上开发了一种多轴向层联机织结构,通过引入面内倾斜纱线改善层联机织结构的面内剪切性能。
| Number of yarn set | Method of interlock | 3D woven preform | ||
| Through-the-thickness | Layer-to-layer plain | Layer-to-layer twill | ||
| 2(warp/weft) | Orthogonal-interlock | 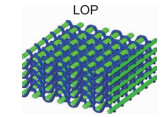 | ||
| Angle-interlock | 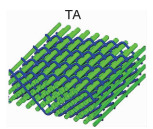 | 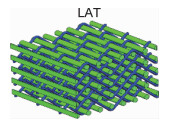 | ||
| 3(warp/weft/stuffer) | Orthogonal-interlock with stuffer yarns | 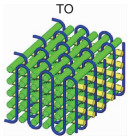 | 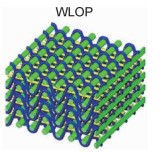 | |
| Angle-interlock with stuffer yarns |  | 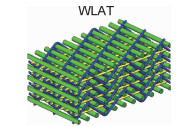 | ||
| 5(warp/weft/stuffer/ ±θ bias) | Orthogonal-interlock with bias yarns | 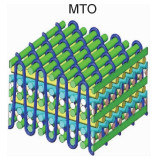 |  | |
典型的树脂基三维机织复合材料的拉伸性能见表 2[14-16]。沿经纱方向,正交三向结构(TO)的拉伸强度明显优于贯穿角联结构(TA)和层层角联斜纹结构(LAT),主要原因是正交三向结构中各方向的纱线基本处于伸直状态,纤维充分发挥了其优异的承载能力。贯穿角联结构(TA)的经向承载能力最差,其结构中所有的接结经纱都是弯曲的,且弯曲程度较大,贯穿了整个结构厚度。当引入衬经纱后,衬经贯穿角联结构(WTA)的经向拉伸性能明显改善。相对于贯穿角联结构,层层角联斜纹结构(LAT)中接结经纱的弯曲程度较小,因此表现出更好的经向抗拉性能。此外,层层角联斜纹结构(LAT-1和LAT-2)中纬纱的含量高于接结经纱,但在结构中纬纱的弯曲程度大于接结经纱[15],综合作用下纬向的拉伸性能小于经向。综上,接结经纱弯曲会导致三维机织复合材料的经向拉伸强度降低,衬经纱的引入可以有效地提高材料的经向承载能力。
| Weave type | Vf/% | Vwarp/% | Vstuffer/% | Vweft/% | Strength/MPa | Modulus/GPa | |||
| Warp | Weft | Warp | Weft | ||||||
| TO[14] | 49.86 | 1.04 | 27.72 | 21.10 | 1358.54 | - | 76.75 | - | |
| WTA[14] | 46.01 | 2.26 | 25.66 | 18.09 | 1276.24 | - | 80.49 | - | |
| TA[14] | 50.98 | 29.56 | N/A | 21.42 | 409.9 | - | 48.54 | - | |
| TO[15] | 51.90 | 8.70 | 14.3 | 28.9 | 1150 | 710 | 69.6 | 59.1 | |
| LAT-1[15] | 50.40 | 16.63 | N/A | 33.77 | 703 | 323 | 53.4 | 33.0 | |
| LAT-2[15] | 59.00 | 28.38 | N/A | 30.62 | 855 | 461 | 62.5 | 43.0 | |
| TO[16] | 51.35 | 3.77 | 21.57 | 26.00 | 711 | 862 | 56.6 | 70.0 | |
| WLAT[16] | 59.16 | 15.65 | 14.36 | 29.15 | 681 | 1029 | 53.9 | 76.6 | |
| WTA[16] | 55.40 | 2.22 | 25.58 | 27.59 | 913 | 924 | 71 | 69.9 | |
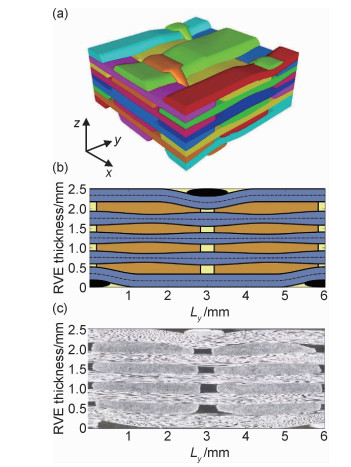
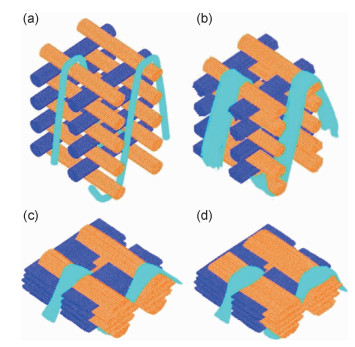
数字图像相关技术(digital image correlation, DIC)可以用来监测三维机织复合材料表面组织结构的局部应变[14-18],如图 1所示。图中显示,三维机织复合材料的表观应变场分布规律与其预制体的编织结构显著相关。试样表观高应变点为复合材料预制体表面纱线的交织点,呈现周期性分布,其分布规律与预制体表面组织结构相同,如平纹规律和斜纹规律。沿经向拉伸时,实验表面经纱交织点为高应变点。在载荷作用下,纱线交织处弯曲的经纱有伸直的趋势,产生较大的应变,当应变累积到一定程度后会引起纱线损伤断裂,导致材料失效。正交三向结构(TO)、贯穿角联结构(TA)和衬经贯穿角联结构(WTA)复合材料具有相同的损伤触发和演化机制,试样受拉伸时发生横向破坏,断口基本平整,断口处少量纤维拔出[14, 16-17]。层层角联斜纹结构(LAT)复合材料的断裂形貌表现出与其受力方向相关的特征[15],如图 2所示,当经纱方向拉伸时试样沿纬纱方向发生横向破坏,断口处纤维平齐断裂,当纬纱方向拉伸时试样沿经纱交织点发生斜向破坏,断口处有纤维拔出。
三维机织复合材料的压缩性能见表 3[14-15, 19]。从表中可以看出,沿预制体的经向含有伸直的衬经纱的试件具有优良的经向压缩性能,如正交三向结构(TO)、衬经贯穿角联机织结构(WTA)和衬经层层直联平纹结构(WLOP)。接结经纱对三维机织复合材料压缩性能的影响取决于其弯曲程度和体积含量的综合作用。角联机织结构中,当接结经纱弯曲程度增大时,材料的压缩性能有下降的趋势,而当沿经向取向的纤维含量增加时,材料的压缩性能则趋于增加。图 3显示了三维机织复合材料的压缩失效模式[14, 20]。在经向压缩载荷下,三维机织复合材料内部增强纤维束产生局部屈曲,周围的基体逐渐破坏,纤维失去支撑、发生断裂,导致材料最终失效。压缩破坏形式主要包括纤维屈曲、纤维横向破坏、基体断裂和界面脱粘等。纤维局部屈曲是主要的破坏形式,这是由于受到纤维交织造成的纤维初始曲屈的影响。当引入伸直的衬经纱后,三维机织复合材料的经向压缩性能明显提高。
| Weave type | Vf/% | Vwarp/% | Vstuffer/% | Vweft/% | Strength/MPa | Modulus/GPa | |||
| Warp | Weft | Warp | Weft | ||||||
| TO[14] | 49.86 | 1.04 | 27.72 | 21.10 | 444.31 | - | 76.18 | - | |
| WTA[14] | 46.01 | 2.26 | 25.66 | 18.09 | 549.59 | - | 92.29 | - | |
| TA[14] | 50.98 | 29.56 | N/A | 21.42 | 197.41 | - | 57.25 | - | |
| TO[15] | 51.90 | 8.70 | 14.3 | 28.9 | 494 | 328 | 55.6 | 53.3 | |
| LAT-1[15] | 50.40 | 16.63 | N/A | 33.77 | 270 | 203 | 47.9 | 31.2 | |
| LAT-2[15] | 59.00 | 28.38 | N/A | 30.62 | 301 | 217 | 59.3 | 41.2 | |
| WLOP[19] | 52.00 | 6.66 | 29.48 | 15.86 | 717 | 320 | 86.7 | 46.5 | |
三维机织复合材料在三点弯曲试验中处于一个复杂的应力状态。加载时试样中同时存在拉应力、压应力和剪切应力。表 4列出了典型结构三维机织复合材料的弯曲性能[14, 21]。从表 4可以看出,当试样长度方向含有伸直度较好的衬经纱时,表现出较高的弯曲性能,如表中的正交三向结构(TO)、衬经贯穿角联结构(WTA)和衬经层层直联平纹结构(WTOP)。图 4为三维机织复合材料弯曲失效形式[14],由图 4可见,试样的失效形式主要有基体失效、纤维断裂和沿着长度方向的分层开裂。此外,纤维交织可以有效抑制裂纹的扩展,预制体交织结构对三维机织复合材料的失效行为有显著的影响。
三维机织复合材料中接结经纱沿厚度方向弯曲并与纬纱相互接结,显著提高了复合材料层间抗剪切性能。Walter等[22]采用短梁剪试验证明了当三维机织复合材料中z向纱体积分数为3%~10%时,对分层裂纹有较好的抑制作用,具有较高的损伤容限。孙绯等[23]研究发现z向纱的体积分数在1%~5%时,对正交三向机织复合材料的层间剪切强度及模量的增强作用明显。表 5为三维机织复合材料面内剪切性能[15, 24-25]。传统的三维机织复合材料面内纱线沿着长度方向和宽度方向分布,材料性能具有明显的各向异性,即沿材料的两个主方向的性能高,而面内剪切性能低,如表 5所列的正交三向结构(TO)和层层角联斜纹结构(LAT)。近年来,通过各种方法在三维机织结构中引入面内斜向纱线,研制的新型多轴向三维机织复合材料(MTO)具有优良的面内剪切性能。图 5给出了采用V形缺口梁剪切试验时,多轴向三维机织复合材料的剪切应变分布和试样剪切断裂形貌[15, 25]。试样的V形缺口处产生明显的剪切应变,纤维发生断裂,断口平整、清晰。
复合材料性能预报准确性在很大程度上取决于其细观结构模型、材料模型以及相关的边界条件和接触条件。三维机织复合材料的细观结构不均匀性和纤维交织引起的局部材料性能的变化使其建模成为一项复杂而具有挑战性的任务。三维机织复合材料细观结构呈现出良好的周期性,存在着宏观结构的代表性细观单元,称为单胞(unit cell)。常见的细观单胞模型有:理想几何模型、解析几何模型、数字单元模型、基于微观扫描重构的实体模型等。
理想几何实体模型是建立在恒定的纱线横截面形状假设基础上获得的织物细观结构理想模型,如图 6所示。纱线的横截面形状假设为椭圆形、矩形、跑道形等,且不受纱线相互挤压、压实等影响,截面形状保持不变。该模型纱线间空隙较大,仅适合于低纤维体积含量的织物预制体的建模。当纤维体积含量较高时,结构内部纱线产生挤压,由于该模型忽略了纱线挤压变形,就会出现相邻纱线相互嵌套交叉现象,无法满足性能分析需要。

|
图 6 理想几何实体单胞模型 Fig. 6 Idealised solid unit cell model |
Isart等[26-27]提出了一种新的解析几何模型,考虑了纱线压实和屈曲对正交三向机织复合材料中衬经纱和接结经纱的截面和分布的影响。该模型采用正弦函数表示由于接结经纱挤压作用造成的纬纱和衬经纱在长度方向上的弯曲形态,并通过特定截面的显微图像,结合结构参数和几何测量,获得预制件内部各纱线的几何形状,如图 7所示。该模型描述三维机织复合材料内部纱线的准真实几何形态,与有限元分析相结合预测复合材料的弹性性能,获得了较好的效果。
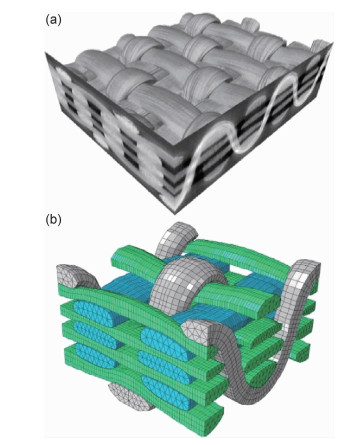
将纤维假设为由一维微小的首尾连续的杆单元或梁单元组成的虚拟纤维,若干根虚拟纤维组成虚拟纱线,虚拟纱线按交织规律组成松散的三维机织结构,通过施加纱线张力模拟预制体的成型过程,松散的三维机织结构变形得到接近真实织物结构的数字单元模型,如图 8所示[27]。当采用梁单元建模时,由于虚拟纤维的截面比真实纤维的截面大得多,获得的虚拟纱线有过高的抗弯刚度,因此采用弹塑性材料模型或自定义梁单元来降低纱线的弯曲刚度[28-29]。Wang等[30-32]提出采用销钉连接的杆单元柔性链对纤维进行建模,当杆单元长度接近于零时,虚拟纤维接近完全柔性。Green等[29]采用梁单元建立了正交三向织物预制体的数字单元模型,模拟了织物的压实过程,通过与微型计算机断层扫描(Micro-CT)重构的织物压实形态对比,模拟结果与实验观测具有较好的一致性,如图 9所示。
随着Micro-CT技术的发展,其在材料内部结构表征和无损检测等领域的应用越来越广泛。采用Micro-CT技术建立的扫描重构模型可以构建复合材料的细观尺度结构,描述结构内部纱线的真实形态,避免了理想化假设,能够反映影响织物结构的任何微观变化,已被用于有限元分析模型建立的输入[33-35],如图 10所示。该方法需要在制得织物预制体或复合材料后才可以进行扫描建模,生成的实体单元结构复杂,转化为有限元分析模型时增加了网格划分的难度。同时,Micro-CT扫描需花费大量时间和昂贵的测试成本。
三维机织复合材料弹性性能分析模型大多是在经典层板理论基础上发展起来的,通过引入各种假设简化分析,获得材料的有效弹性性能的封闭解。Cox和Dadkhah[36]考虑了接结经纱面外弯曲的影响提出了改进的取向平均模型,通过引入刚度折减因子对纤维的工程弹性常数进行折减,分别应用等应力或等应变假设,采用取向平均模型获得三维机织复合材料的宏观平均弹性常数。Tan等[37]采用等应力和等应变混合模型预报了三维机织复合材料的弹性性能和热弹性性能,代表性单胞被分割成由四种微单元堆砌而成的集合体,四种微单元分别代表由树脂与经纱、纬纱或衬经纱组成的单向复合材料,按微单元堆砌顺序分为XYZ, YXZ, ZXY和ZYX模型,分别应用等应力或等应变假设,计算获得的等效弹性性能与试验结果相吻合。Buchanan等[38]提出了一种分析三维机织复合材料等效弹性常数的方法,代表性单胞分割为若干层薄层,薄层又划分为许多横条,每个横条假设为纤维与树脂组成的单向复合材料,假设等应力或等应变,由横条刚度获得薄层的刚度,再假设等应力或等应变,由薄层刚度组装计算获得代表性单胞的刚度,其中等应变假设应用于纤维方向,等应力假设应用于垂直纤维方向。朱永新等[39]采用余弦曲线模拟经纱走向,通过沿经向切片积分的方法计算三维机织复合材料经向拉伸模量,预测精度优于传统体积平均方法。
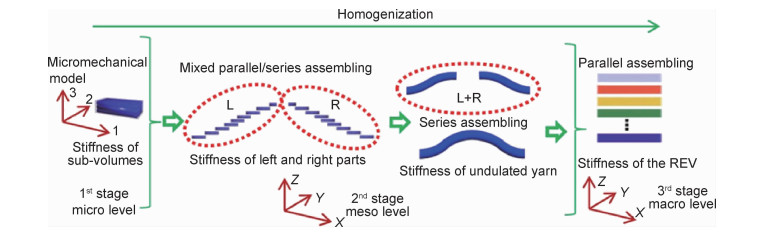
Hallal等[40-41]提出了一种高效的三维机织复合材料弹性分析模型,即三尺度均匀化模型(3SHM),如图 11所示。该模型中三维机织复合材料均匀划分为3个尺度,即微观尺度、细观尺度和宏观尺度。
(1) 微观尺度:接结经纱或纬纱微观上离散为许多纱线子单元。在局部坐标系中,纱线子单元假设为单向纤维增强复合材料,为橫观各向同性材料,等效弹性性能由Chamis模型[42]获得。
(2) 细观尺度:接结经纱由左、右弯曲段和直线段组成。首先通过坐标转换将接结经纱子单元弹性性能由局部坐标转换到整体坐标;其次,采用刚度体积平均法由弯曲段的子单元分别集成接结经纱的左、右弯曲段的刚度;再采用柔度体积平均法由左、右弯曲段集成纱线整体弯曲段的刚度;最后采用刚度体积平均法由弯曲段和直线段获得接结经纱的整体刚度。纬纱在结构中保持良好的伸直状态,其离散的子单元具有相同的弹性性能,因此采用刚度体积平均法获得的纬纱的整体刚度与其子单元的刚度相同。
(3) 宏观尺度:三维机织复合材料代表性单元包含接结经纱、纬纱和树脂基体。根据各相材料的刚度矩阵和体积含量,利用刚度体积平均法获得复合材料的等效弹性性能。
3SHM方法可以模拟不同结构的纺织复合材料的弹性性能,与已有的实验数据和数值模拟结果相比,该模型预报结果具有较高的精度。
Kim等[43]采用有限元方法模拟材料性能试验,预报了三维机织复合材料的弹性性能,代表性单元体中的衬经纱、纬纱和接结经纱采用实体单元离散,复合材料试样由离散的代表性单元体沿经向和纬向堆砌组合而成,边界条件模拟材料实验加载条件,由虎克定律获得材料的弹性性能。Wang等[44]提出了一种双尺度有限元分析方法预报了三维机织复合材料的弹性性能,微观上建立了单向纤维增强复合材料的有限元模型,采用周期性边界条件计算获得了纱线的弹性性能,宏观上建立了代表性单胞的有限元实体模型,采用周期性边界条件分析了代表性单胞的应力分布,获得了材料的等效弹性性能。
Jia等[45]建立了多尺度代表单元模型(Multi-scale model),研究了三维机织复合材料在准静态拉伸载荷作用下的非线性黏弹性响应和损伤机理,模拟了材料整体损伤的触发、损伤演化积累和材料的最终破坏失效,与实验结果具有较好的一致性。Zhong等[46]考虑到三维机织复合材料制造过程中纤维束会产生弯曲波动,根据实际材料中纤维束弯曲波动随机统计规律提出了一种随机波动模型(RW model),用来研究三维机织复合材料的刚度和强度特性,与实验结果进行了对比验证,并讨论了纤维束随机波动对材料力学性能的影响。Dai等[47]为了研究不同失效准则对模拟大型结构的影响,建立了两种不同尺度下的数值模型,模拟分析了两种不同结构三维机织复合材料的力学性能和损伤行为,与实验测试模量和强度相比误差在20%以内。表 6给出了这几种强度模型的预测值和实验值的对比结果[45-47]。
| Model | Loading type | Modulus/GPa | Error/% | Strength/MPa | Error/% | ||
| Experimented | Simulated | Experimented | Simulated | ||||
| Multi-scale model[45] | Tensile | 20.94 | 20.3 | 3.06 | 437.38 | 475.5 | 8.72 |
| RW model[46] | Tensile | 55.1 | 60.2 | 9.26 | 892 | 1015 | 13.79 |
| RW model[46] | Compressive | 55.3 | 60.3 | 9.04 | 491 | 553 | 12.63 |
| Unit cell model[47] | Tensile | 76.75 | 87.64 | 14.19 | 1368.91 | 1533.86 | 12.05 |
| Mosaic model[47] | Tensile | 76.75 | 86.45 | 12.64 | 1368.91 | 1492.67 | 9.04 |
三维机织预制体保持了增强纤维的连续性和编织结构的完整性,以其增强的三维机织复合材料具有抗分层、抗冲击和耐疲劳等优异性能,在航空航天领域得到了广泛应用[48-50]。2004年法国斯奈克玛(Snecma)发动机公司在最新一代LEAP-X1C发动机上采用了三维机织技术和RTM技术研制出复合材料发动机风扇叶片。新一代GE9X(配装Boeing 777X),采用了第四代碳纤维三维机织复合材料叶片,如图 12所示[52],叶片数量16片,比GE90(22片)和GEnx(18片)叶片数量再次减少,从而减轻质量,提高发动机性能。2008年GEnx发动机(配装Boeing787)首次采用了碳纤维二维三轴复合材料机匣,将复合材料风扇机匣的研制水平推上了一个新的台阶。新一代的LEAP发动机采用了三维机织复合材料风扇机匣,如图 13所示[53],整个机匣预制件(包括法兰)一次编织成型,提高了机匣的耐久性和包容性,减少发动机维护成本。Messier-Bugatti-Dowty公司为Boeing 787研发了碳纤维复合材料主起落架支架,如图 14所示,这是在商用飞机起落架上首次使用结构复合材料[51]。与金属支架相比,三维机织复合材料支架减轻了结构质量,满足复杂的轴向和剪切工况,可抵抗鸟类或跑道碎片的撞击和起降周期性疲劳,提高了服役可靠性。
三维机织预制体具有卓越的异型构件仿形能力,可实现复合材料构件的近净尺寸成型,如采用三维机织工艺仿形编织的π型梁、发动机转子、罩体预制体、截锥体、喷管、燃烧室等,见图 15[49, 55-56]。采用三维机织预制体制成的陶瓷基、碳碳等复合材料具有质量轻、强度高、耐高温、耐冲击、耐烧蚀等优异性能,是研制航天结构、发动机、制动装置和热防护等主要系统和部位的理想材料,是实现超高温环境下主承力构件防热/结构一体化设计的关键材料,具有广泛的应用前景。
三维机织复合材料是纤维增强复合材料的高级形式,克服了传统层合复合材料层间性能弱的缺点,具有抗冲击、耐疲劳等优异性能,在主承力结构领域具有广泛的应用前景。三维机织复合材料具有多样化的细观结构和可调节的纤维取向分布,给材料的优化设计提供了广阔余地,同时也给材料性能分析带来了巨大的困难。经过近30年的发展,三维机织复合材料的力学性能研究取得了实质性的成果,为该类材料的工程应用提供了理论支撑,但仍然有一些关键问题亟待解决:
(1) 三维机织复合材料设计尚未形成公认且成熟的方法。材料刚度的正向模拟设计方法较多且精度尚可,但材料细观编织结构的逆向设计缺乏系统方法,同时材料性能数据库亟待建立。
(2) 三维机织复合材料的可靠性研究不足。材料准静态力学行为的阐述相对较深刻,但其疲劳性能、动态力学性能、多场耦合力学行为等亟待进一步的系统化研究。
(3) 三维机织复合材料预制体成型自动化程度低,特别是复杂结构预制体成型人工辅助程度高,造成编织结构不均匀、张力控制不稳定性、产品质量一致性差。开发高效、自动、柔性化的纤维预制体成型高端装备是三维机织复合材料工程推广应用的技术关键。
| [1] |
陈利, 赵世博, 王心淼. 三维纺织增强材料及其在航空航天领域的应用[J]. 纺织导报, 2018(增刊1): 80-87. CHEN L, ZHAO S B, WANG X M. Development and application of 3D textile reinforcements in the aerospace field[J]. China Textile Leader, 2018(Suppl 1): 80-87. |
| [2] |
戎琦. 三维机织复合材料的织造技术[J]. 纤维复合材料, 2007, 24(1): 31-33. RONG Q. Weaving technology of 3D woven composites[J]. Fiber Composites, 2007, 24(1): 31-33. |
| [3] |
CHEN X, TAYLOR L W, TSAI L J. An overview on fabrication of three-dimensional woven textile preforms for composites[J]. Textile Research Journal, 2011, 81(9): 932-944. |
| [4] |
孙颖, 王国军, 张典堂, 等. UHMWPE/乙烯基酯2.5 D角联锁机织复合材料动态压缩性能实验研究[J]. 材料工程, 2011(4): 38-42. SUN Y, WANG G J, ZHANG D T, et al. Experimental investigation on dynamic compression properties of UHMWPE/vinyl ester 2.5 dimensional angle interlocked woven composites[J]. Journal of Materials Engineering, 2011(4): 38-42. |
| [5] |
DAI S, CUNNINGHAM P R, MARSHALL S, et al. Open hole quasi-static and fatigue characterisation of 3D woven composites[J]. Composite Structures, 2015, 131: 765-774. |
| [6] |
SUN B, NIU Z, JIN L, et al. Experimental investigation and numerical simulation of three-point bending fatigue of 3D orthogonal woven composite[J]. Journal of the Textile Institute, 2012, 103(12): 1312-1327. |
| [7] |
HALLAL A, YOUNES R, FARDOUN F. Review and comparative study of analytical modeling for the elastic properties of textile composites[J]. Composites:Part B, 2013, 50: 22-31. |
| [8] |
ANSAR M, XINWEI W, CHOUWEI Z. Modeling strategies of 3D woven composites:a review[J]. Composite Structures, 2011, 93(8): 1947-1963. |
| [9] |
GEREKE T, CHERIF C. A review of numerical models for 3D woven composite reinforcements[J]. Composite Structures, 2019, 209: 60-66. |
| [10] |
张一帆, 马明, 陈利. 多层多向织物复合材料力学性能分析[J]. 宇航材料工艺, 2013, 43(2): 31-34. ZHANG Y F, MA M, CHEN L. Mechanical properties of composites reinforced by multi-ply multi-axial preforms[J]. Aerospace Materials and Technology, 2013, 43(2): 31-34. |
| [11] |
BILISIK K. Multiaxis three-dimensional weaving for composites:a review[J]. Textile Research Journal, 2012, 82(7): 725-743. |
| [12] |
LABANIEH A R, LEGRAND X, KONCAR V, et al. Development in the multiaxis 3D weaving technology[J]. Textile Research Journal, 2016, 86(17): 1869-1884. |
| [13] |
陈利, 张一帆, 王心淼, 等.一种含斜向纱线的角联锁织物及其织造方法, CN106987979A[P/OL]. 2017-07-28[2019-05-06], https: //kns.cnki.net/kns/brief/default_result.aspx. CHEN L, ZHANG Y F, WANG X M, et al. Angle interlocking fabric with bias yarn and its method of manufacture, CN106987979A[P/OL]. 2017-07-28[2019-05-06], https: //kns.cnki.net/kns/brief/default_result.aspx. |
| [14] |
DAI S, CUNNINGHAM P R, MARSHALL S, et al. Influence of fibre architecture on the tensile, compressive and flexural behaviour of 3D woven composites[J]. Composites:Part A, 2015, 69: 195-207. |
| [15] |
WARREN K C, LOPEZ-ANIDO R A, GOERING J. Experimental investigation of three-dimensional woven composites[J]. Composites:Part A, 2015, 73: 242-259. |
| [16] |
SALEH M N, YUDHANTO A, POTLURI P, et al. Characterising the loading direction sensitivity of 3D woven composites:Effect of z-binder architecture[J]. Composites:Part A, 2016, 90: 577-588. |
| [17] |
CASTANEDA N, WISNER B, CUADRA J, et al. Investigation of the Z-binder role in progressive damage of 3D woven composites[J]. Composites:Part A, 2017, 98: 76-89. |
| [18] |
IVANOV D S, LOMOV S V, BOGDANOVICH A E, et al. A comparative study of tensile properties of non-crimp 3D orthogonal weave and multi-layer plain weave E-glass composites. part 2:comprehensive experimental results[J]. Composites:Part A, 2009, 40(8): 1144-1157. |
| [19] |
MAHADIK Y, HALLETT S R. Effect of fabric compaction and yarn waviness on 3D woven composite compressive properties[J]. Composites:Part A, 2011, 42(11): 1592-1600. |
| [20] |
仲苏洋.三维机织复合材料损伤演化与失效行为研究[D].哈尔滨: 哈尔滨工业大学, 2015. ZHONG S Y. Investigation of damage evolution and failure of the three-dimensional woven composites[D]. Harbin: Harbin Institute of Technology, 2015. |
| [21] |
ZHANG D, SUN M, LIU X, et al. Off-axis bending behaviors and failure characterization of 3D woven composites[J]. Composite Structures, 2019, 208: 45-55. |
| [22] |
WALTER T R, SUBHASH G, SANKAR B V, et al. Monotonic and cyclic short beam shear response of 3D woven composites[J]. Composites Science and Technology, 2010, 70(15): 2190-2197. |
| [23] |
孙绯, 陈利, 孙颖, 等. z向纱对三维正交复合材料层间剪切性能影响[J]. 固体火箭技术, 2015, 38(1): 111-115. SUN F, CHEN L, SUN Y, et al. Effects of the z binder on interlaminar shearing properties of 3D orthogonal composites[J]. Journal of Solid Rocket Technology, 2015, 38(1): 111-115. |
| [24] |
BILISIK K. Multiaxis 3D woven preform and properties of multiaxis 3D woven and 3D orthogonal woven carbon/epoxy composites[J]. Journal of Reinforced Plastics and Composites, 2010, 29(8): 1173-1186. |
| [25] |
郭慧.多层多向三维机织物细观结构研究[D].天津: 天津工业大学, 2014. GUO H. Study on the microstructure of multi-layer and multi-axial three-dimensional woven fabrics[D]. Tianjin: Tianjin Poly-technic University, 2014. |
| [26] |
ISART N, MAYUGO J A, BLANCO N, et al. Geometric model for 3D through-thickness orthogonal interlock composites[J]. Composite Structures, 2015, 119: 787-798. |
| [27] |
ISART N, EL SAID B, IVANOV D S, et al. Internal geometric modelling of 3D woven composites:a comparison between different approaches[J]. Composite Structures, 2015, 132: 1219-1230. |
| [28] |
DURVILLE D. Simulation of the mechanical behaviour of woven fabrics at the scale of fibers[J]. International Journal of Material Forming, 2010, 3(2): 1241-1251. |
| [29] |
GREEN S D, LONG A C, EL SAID B S F, et al. Numerical modelling of 3D woven preform deformations[J]. Composite Structures, 2014, 108: 747-756. |
| [30] |
WANG Y, SUN X. Digital-element simulation of textile processes[J]. Composites Science and Technology, 2001, 61(2): 311-319. |
| [31] |
WANG Y, MIAO Y, SWENSON D, et al. Digital element approach for simulating impact and penetration of textiles[J]. International Journal of Impact Engineering, 2010, 37(5): 552-560. |
| [32] |
ZHOU G, SUN X, WANG Y. Multi-chain digital element analysis in textile mechanics[J]. Composites science and Technology, 2004, 64(2): 239-244. |
| [33] |
NAOUAR N, VIDAL-SALLE E, SCHNEIDER J, et al. 3D composite reinforcement meso FE analyses based on X-ray computed tomography[J]. Composite Structures, 2015, 132: 1094-1104. |
| [34] |
STRAUMIT I, LOMOV S V, WEVERS M. Quantification of the internal structure and automatic generation of voxel models of textile composites from X-ray computed tomography data[J]. Composites:Part A, 2015, 69: 150-158. |
| [35] |
DESPLENTERE F, LOMOV S V, WOERDEMAN D L, et al. Micro-CT characterization of variability in 3D textile architecture[J]. Composites Science and Technology, 2005, 65(13): 1920-1930. |
| [36] |
COX B N, DADKHAH M S. The macroscopic elasticity of 3D woven composites[J]. Journal of Composite Materials, 1995, 29(6): 785-819. |
| [37] |
TAN P, TONG L, STEVEN G P. Micromechanics models for mechanical and thermomechanical properties of 3D through-the-thickness angle interlock woven composites[J]. Composites:Part A, 1999, 30(5): 637-648. |
| [38] |
BUCHANAN S, GRIGORASH A, ARCHER E, et al. Analy-tical elastic stiffness model for 3D orthogonal interlock composites[J]. Compos Sci Technol, 2010, 70(11): 1597-1604. |
| [39] |
朱永新, 崔海涛, 温卫东. 2.5维机织复合材料经向拉伸弹性模量预测与试验验证[J]. 复合材料学报, 2013, 30(3): 198-204. ZHU Y X, CUI H T, WEN W D. Elastic property prediction and experimental verification in the warp direction of 2.5D woven composites[J]. Acta Materiae Compositae Sinica, 2013, 30(3): 198-204. |
| [40] |
HALLAL A, YOUNES R, FARDOUN F, et al. Improved analytical model to predict the effective elastic properties of 2.5 D interlock woven fabrics composite[J]. Composite Structures, 2012, 94(10): 3009-3028. |
| [41] |
HALLAL A. Modeling of elastic properties of textile composites[D]. Saint-Quentin: University of Versailles-Saint-Quentin en Yvelines, 2013.
|
| [42] |
CHAMIS C C. Mechanics of composite materials:past, present, and future[J]. Journal of Composites, Technology and Research, 1989, 11(1): 3-14. |
| [43] |
KIM S J, JI K H, PAIK S H. Numerical simulation of mechanical behavior of composite structures by supercomputing technology[J]. Advanced Composite Materials, 2008, 17(4): 373-407. |
| [44] |
WANG X F, WANG X W, ZHOU G M, et al. Multi-scale analyses of 3D woven composite based on periodicity boundary conditions[J]. Journal of Composite Materials, 2007, 41(14): 1773-1788. |
| [45] |
JIA X, XIA Z, GU B. Nonlinear viscoelastic multi-scale repetitive unit cell model of 3D woven composites with damage evolution[J]. International Journal of Solids and Structures, 2013, 50(22/23): 3539-3554. |
| [46] |
ZHONG S, GUO L, LIU G, et al. A random waveness model for the stiffness and strength evaluation of 3D woven composites[J]. Composite Structures, 2016, 152: 1024-1032. |
| [47] |
DAI S, CUNNINGHAM P R. Multi-scale damage modelling of 3D woven composites under uni-axial tension[J]. Composite Structures, 2016, 142: 298-312. |
| [48] |
MRAZOVA M. Advanced composite materials of the future in aerospace industry[J]. Incas Bulletin, 2013, 5(3): 139. |
| [49] |
MISRA A. Composite materials for aerospace propulsion related to air and space transportation[M].//NJUGUNA Lightweight Composite Structures in Transport.Kidlington: Woodhead Publishing, 2016: 305-327.
|
| [50] |
NAYAK N V. Composite materials in aerospace applications[J]. International Journal of Scientific and Research Publications, 2014, 4(9): 1-10. |
| [51] |
TAKAHASHI N, SATO T, FUJIWARA K, et al. Fod characteristics of titanium metal matrix composite (tmc) to apply aircraft landing gear structure[C].//St. Petersburg: Proceedings of 29th Congress of the International Council of the Aeronautical Sciences, 2014: 52-61.
|
| [52] |
ALBANY. Leap fan blade[EB/OL].[2019-05-06]. https://www.albint.com/business/aec/en-us/aerspace/Pages/LEAP-Fan-Blade.aspx.
|
| [53] |
ALBANY. Leap fan casing[EB/OL].[2019-05-06]. https://www.albint.com/business/aec/en-us/aerospace/pages/LEAP-Fan-Casing.aspx.
|
| [54] |
ZOE GRANT. Chris wilson messier-bugatti-dowty safran group[EB/OL].[2019-05-06]. https://docplayer.net/55755570-Chris-wilson-messier-bugatti-dowty-safran-group.html.
|
| [55] |
BITEAM. Product sheet standard pi profiles[EB/OL].[2019-05-06]. http://www.biteam.com/.
|
| [56] |
MOURITZ A P, BANNISTER M K, FALZON P J, et al. Review of applications for advanced three-dimensional fibre textile composites[J]. Composites:Part A, 1999, 30: 1445-1461. |
 2020, Vol. 48
2020, Vol. 48