文章信息
- 朱礼宝, 戴文喜, 李永清, 朱锡, 朱子旭
- ZHU Li-bao, DAI Wen-xi, LI Yong-qing, ZHU Xi, ZHU Zi-xu
- 考虑层间和界面的玻璃纤维/环氧复合材料吸湿扩散实验和仿真
- Experimental/numerical investigation of moisture diffusion in glass/epoxy composites in consideration of interlamination and interphase
- 材料工程, 2019, 47(11): 84-91
- Journal of Materials Engineering, 2019, 47(11): 84-91.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000016
-
文章历史
- 收稿日期: 2019-01-06
- 修订日期: 2019-07-22
2. 中国舰船研究设计中心, 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
纤维增强树脂基复合材料具有高比强度、高比刚度和设计性良好等特点,广泛应用于航空航天、交通运输和海洋工程等领域。复合材料在使用过程中可能会暴露于环境载荷之下,导致性能发生弱化。其中,水分是引起复合材料性能变化的重要因素之一。对于增强体为玻璃纤维、碳纤维等无机纤维的树脂基复合材料,纤维一般不吸收水分,吸湿主体为树脂基体和纤维/基体界面。水进入复合材料后与基体发生反应,进一步造成复合材料的可逆(如基体膨胀、塑化)或不可逆变化(如基体水解、分子链松弛、空穴,纤维基体界面脱粘),影响复合材料的使用性能。研究复合材料的吸湿性能是评估其长期使用寿命的首要任务。
水进入树脂基体属于水浓度梯度驱动的扩散过程[1],可用Fick模型进行描述。ASTM D5229描述了获取复合材料吸湿扩散系数的典型方法,当层合板尺寸为150mm×150mm×1.5mm时,其吸湿符合一维扩散过程,可用简化的公式进行拟合。然而在许多情况下,水分从多个方向进入复合材料,需要考虑复合材料的三维扩散系数,可采用树脂封边[2]和三维扩散方法获得[3-4]。结果表明,对于单向复合材料,沿纤维方向的扩散系数可能为垂直纤维方向扩散系数的2~4倍。在材料的扩散系数研究基础上,Canal等[5]研究了复合材料胶结接头的吸湿行为;谭翔飞等[6]研究了复合材料加筋壁板的吸湿行为,并提出了阶段吸湿模型。
同时,已有学者采用理论模型和有限元模型对单向复合材料的吸湿扩散系数进行了预测。Shen等[7]和Halpin[8]类比热传导过程,给出了单向复合材料横向相对等效吸湿扩散系数的表达式。研究者在Halpin模型的基础上建立了自洽理论模型,预测了纤维体积分数、界面和孔隙等因素对等效吸湿扩散系数的影响[9-10]; 采用有限元法建立了复合材料湿扩散的稳态单胞模型,计算了纤维体积分数和温度对扩散系数的影响[11-12]。水在复合材料中的扩散属于瞬态扩散过程,Vaddadi等[13]采用卡尔曼滤波和二维瞬态有限元模型相结合的方法,由复合材料的吸湿扩散曲线反推出了基体材料的吸湿扩散参数。还有研究者建立了二维瞬态扩散模型,研究了纤维/基体界面对横向吸湿扩散系数的影响[14-15]。
层间是复合材料层合板的重要特征,对复合材料的性能有较大影响。但是现有研究中通常只考虑纤维和界面对复合材料扩散系数的作用,没有涉及层间的影响。针对这一问题,本工作开展了复合材料的三维吸湿实验,建立了包含复合材料层间和界面的有限元吸湿扩散模型,研究层间和界面对复合材料扩散系数的影响。
1 实验材料与方法 1.1 实验材料实验所用单向S玻纤/环氧复合材料由咸宁海威复合材料有限公司生产。单向S玻纤布型号SWU414,玻纤密度2.54g/cm3。纬向热熔纱起固定作用,线密度12 tex,1.6根/cm。基体树脂采用双酚A型环氧树脂,牌号1001,固化剂为改性聚醚胺固化剂。采用真空成型法制备单向铺层的复合材料板,共41层,成型后板厚14.64mm,单层厚度3.57×10-1mm。采用浇注法制成1.8mm厚度的环氧树脂板,其配比和固化工艺与复合材料一致。
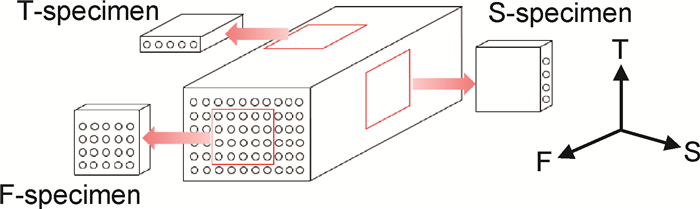
部分研究采用树脂封边的方法制作复合材料单向吸湿试样,该方法操作简单,但无法保证树脂封边的密封性。为获得复合材料的三维扩散系数,如图 1所示,通过数控加工中心,沿单向铺层复合材料板的3个方向切割出10mm×10mm×1.5mm的吸湿试样。定义沿单向铺层复合材料板的纤维方向为F方向,垂直于纤维且沿纬纱为S方向,厚度方向为T方向,分别标记这3个方向的吸湿试样为F试样、S试样和T试样。采用水刀将树脂浇注体切割成10mm×10mm×1.8mm的吸湿试样。最后用600#的砂纸打磨复合材料和树脂试样,以保证试样边缘平整,无毛刺。
|
图 1 复合材料试样示意图 Fig. 1 Schematic diagram of composite samples |
采用排水法,测得复合材料的密度为1.81g/cm3。参考标准ASTM D3171-15,采用烧蚀法测定复合材料的纤维体积分数为46.88%,质量分数65.74%。同时,为观测复合材料的纤维截面,需对试样进行抛光处理,过程如下[15-16]:
(1) 将试样置于硅胶模具中,配置透明树脂对试样进行浇注并室温固化。
(2) 对树脂浇注试样进行打磨。首先采用600#,1200#,1500#的砂纸分别打磨试样,水润滑,磨盘速度300r/min。然后将砂纸换成缎面丝绸,用0.05μm粒度的氧化铝抛光剂进行抛光。每次打磨后均用超声波清洗仪对试样进行清洗。
试样制作完毕后,在光学显微镜下观察复合材料的纤维分布。采用开源软件Image J对图像进行处理,统计复合材料的纤维体积分数及纤维直径。同时,为测量界面层的厚度,采用Bruker Dimension IconTM原子力显微镜对试样进行扫描,探针直径20nm,扫描范围5μm×5μm,扫描频率256×256,扫描间距约19nm。
1.2.2 吸湿实验采用称重法测定复合材料的吸湿性能。参考标准ASTM D5229,首先将复合材料和纯树脂吸湿试样置于40℃烘箱中去除初始水分,直至试样质量不再变化。随后,将吸湿试样放于装有去离子水的烧杯中,并将烧杯放置在50℃水浴锅中以加速吸湿过程,每组重复3个试样。定期取出试样进行称重,分析天平精度0.1mg,称重前将试样表面水分充分吸干。按式(1)计算t时刻水的吸收率Wt:
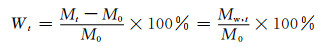
|
(1) |
式中:Mt为t时刻试样质量;M0为试样初始质量;Mw, t为t时刻试样吸收的质量。试样到达饱和吸湿后,吸收的水的质量不再随时间变化,称作饱和吸湿量,用Mw, ∞表示,对应的饱和吸湿率为W∞。
2 实验结果 2.1 光学显微镜及AFM图 2(a)所示为处理后复合材料纤维区的典型光学显微镜图,图中可见纤维分布随机,纤维大小不一。随机选取10处纤维区,计算得到纤维区平均纤维体积分数Af=56.73%。统计纤维直径,得到纤维直径分布于8~11μm之间的占50%以上。图 2(b)包含层间区,计算得到平均层间厚度ti = 6.20×10-2mm。已知复合材料单层总厚度为tl=3.57×10-1mm,则复合材料的纤维体积分数为AC= Af(tl- ti)/tl=46.87%,与烧蚀法所得结果基本一致,说明光学显微图计算结果是正确的。

|
图 2 复合材料光学显微镜图 (a)纤维区;(b)层间 Fig. 2 Optical microscopic images of composites (a) fiber area; (b)interlamination |
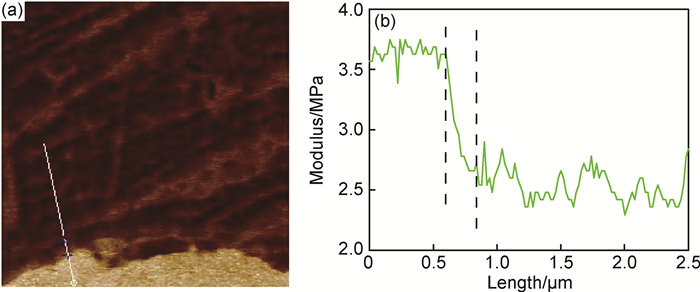
图 3为AFM模量测量模式的结果图。图 3(a)中黄色显示为纤维,深红色显示为基体。沿纤维中心至基体选取一条路径,其模量分布典型结果如图 3(b)所示,图中可清晰分辨纤维、界面和基体3个区域。随机选取10条路径,计算得到界面层平均厚度为0.20μm。
|
图 3 AFM测试结果 (a) AFM模量图; (b)典型模量分布 Fig. 3 Results of AFM tests (a) AFM modulus mode; (b)typical modulus distribution |
水进入纯树脂浇筑体和复合材料基体属于水浓度梯度驱动的扩散过程,可用Fick模型的瞬态扩散过程进行描述。对于一维和三维吸湿状态,其表达式分别如式(2)和式(3)所示[17]:
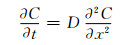
|
(2) |
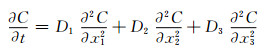
|
(3) |
式中:C为水分浓度,mol·m-3;D为扩散系数,m2·s-1;x为沿扩散方向的坐标。恒温恒湿条件下一般假设D为定值。
对初始为干燥状态的材料,其在一维和三维吸湿状态下吸湿量与时间的关系分别如式(4)和式(5)所示:
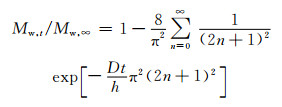
|
(4) |
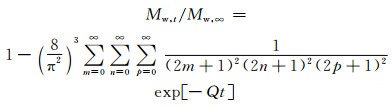
|
(5) |
其中
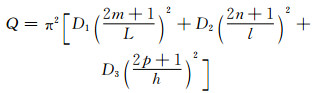
|
(6) |
式中:L,l,h为沿扩散方向的材料尺寸。
Pierrron提出了一个获取材料吸湿扩散系数的拟合方法,定义目标函数:
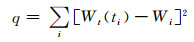
|
(7) |
其中Wi为ti时刻的实验值,Wt(ti)为式(4)或式(5)在ti时刻的计算值,通过求q的最小值得到材料的吸湿扩散系数。
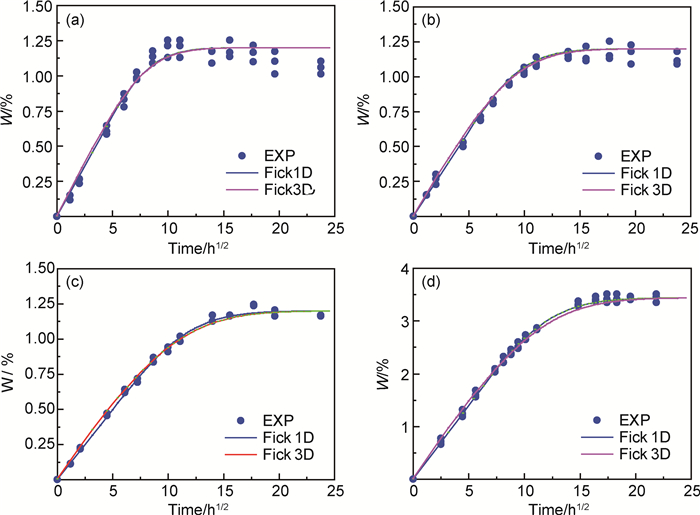
2.2.2 吸湿实验结果图 4所示为复合材料和树脂浇注体的吸湿测试结果及拟合结果,图中可以看出,材料的吸湿量随时间的开方先线性增加,后基本保持不变,符合Fick扩散模型。复合材料的饱和吸湿率WC约为1.20%(质量分数,下同),树脂浇筑体的饱和吸湿率WR约为3.44%。已知复合材料纤维的质量分数(mF)为65.74%,可计算出复合材料的饱和吸湿率为WC=WR×(1-mF)=1.18%,与实验结果基本一致。
|
图 4 复合材料和树脂吸湿实验结果和拟合曲线 (a)F方向; (b)S方向; (c)T方向; (d)纯树脂 Fig. 4 Experimental results and fit curves of composites and resin (a)direction F; (b)direction S; (c)direction T; (d)pure resin |
对复合材料和纯树脂的吸湿实验数据进行一维和三维Fick公式拟合,所得结果如图 4和表 1所示。可以看出,一维和三维Fick模型拟合均能较好地反应复合材料和纯树脂的吸湿过程,但三维模型拟合的吸湿扩散系数均小于一维模型结果,这是因为对于本工作所采用的试样,其尺寸不满足一维吸湿拟合的要求,试样实际为三维吸湿过程。一维吸湿拟合将3个方向的吸湿过程简化为一个方向,所得结果自然大于该方向原本的扩散系数值。对比复合材料与纯树脂的三维扩散系数,复合材料F方向值最大,为纯树脂扩散系数的1.55倍;S方向值略大于纯树脂扩散系数,而T方向值最小,为纯树脂扩散系数的63.7%。研究表明,在垂直于纤维方向,纤维的阻碍作用会减小扩散系数,而界面则会起到增强作用,且一般认为垂直于纤维方向的扩散系数相同[14, 18]。本工作中,复合材料垂直于纤维两个方向的扩散系数相差较大,仅用纤维阻碍及界面扩散无法解释,需要进一步研究复合材料的扩散机理。
| Method | Neat resin | Composites | |||
| Dresin | DF | DS | DT | ||
| 1D equation | 4.32×10-3 | 6.16×10-3 | 4.45×10-3 | 2.98×10-3 | |
| 3D equation | 3.50×10-3 | 5.41×10-3 | 3.58×10-3 | 2.23×10-3 | |
根据实验结果可知,复合材料沿纤维方向的扩散系数大于纯树脂的扩散系数,两个垂直于纤维方向的扩散系数不一致。结合前期光学显微镜观测结果,可以推测这一现象是由纤维、界面、纬纱和层间共同导致的。对于纬纱,由于其每层数量较少,因而假设其只对沿纬纱方向的扩散系数造成影响,其他方向无影响。
为进一步研究上述因素对扩散的影响,采用有限元软件ABAQUS中的物质扩散模块对复合材料的吸湿过程进行模拟。物质扩散模块中,控制方程由扩散相的物质守恒定义,Fick扩散是其中一种模式。有限元模型输入的材料属性为扩散系数D和溶解度s,边界条件为标准化浓度,定义为φ=c/s,其中c为扩散相的浓度。当网格包含共享节点的不同材料时,标准化浓度在不同材料界面上是连续的。根据实验结果,有限元模型中取纤维直径10μm,界面厚度0.2μm,复合材料纤维体积分数46.88%。假设复合材料基体的性能与纯树脂性能一致,吸湿扩散系数为3.50×10-3mm2·h-1,饱和吸湿率为3.44%;纤维的扩散系数和饱和吸湿率均为零。为简化模型,不考虑纤维与纤维相接触的情况,不建立纬纱的模型。
本工作首先建立S方向和T方向的典型二维瞬态扩散模型,以直观对比层间对扩散的影响。随后,建立复合材料三维稳态扩散胞元,量化层间、界面和纬纱对复合材料三维扩散系数的影响。
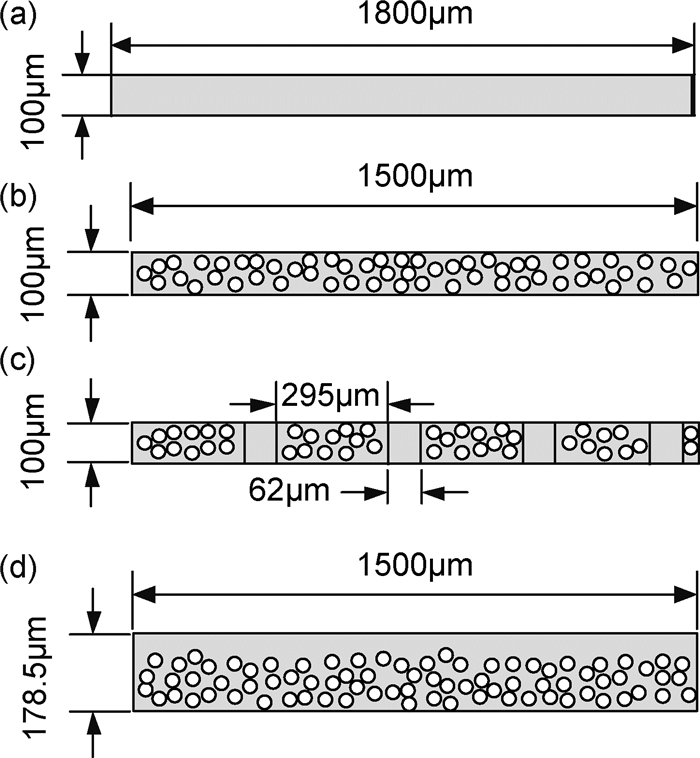
3.1 2D瞬态模拟 3.1.1 2D瞬态模型如图 5所示,对纯树脂基体,建立图 5(a)所示模型,模型尺寸1800μm×100μm。对复合材料的T方向,建立图 5(b)所示的Full模型和图 5(c)所示的Interlamination模型,模型尺寸1500μm×100μm。Full模型不考虑层间,在区域中随机生成896根纤维。Interlamination模型考虑纤维区和层间区,纤维区长295μm,随机生成213根纤维,层间区长62μm,无纤维。对复合材料的S方向,建立图 5(d)所示模型,模型尺寸1500μm×178.5μm,其中纤维区宽度147.5μm,共分布1598根纤维,基体区宽度31μm,无纤维。复合材料2D模型不考虑界面的影响。
|
图 5 2D有限元模型 (a)纯树脂模型;(b)T方向Full模型;(c)T方向Interlamination模型;(d)S方向模型 Fig. 5 2D finite element model (a)resin model; (b)Full model for T direction; (c)Interlamination model for T direction; (d)S direction model |
将上述2D模型设置为瞬态扩散过程,瞬态分析步中,时间积分的准确性由DCMAX变量控制,即每一时间步所允许的最大标准化浓度变化值。经试算,本工作中取DCMAX为0.01,同时对树脂模型取2μm尺寸进行网格划分,对复合材料模型取0.5μm尺寸进行网格划分。在模型两侧施加单位标准化浓度,即边界始终保持饱和吸湿状态。
3.1.2 瞬态模型结果图 6所示为2D瞬态模型计算结果与解析结果的对比,其中解析结果为取树脂或复合材料的三维扩散系数依据式(3)计算所得。图 6(a)为树脂有限元模型模拟结果与解析结果对比,可以看出,有限元模拟结果与解析结果吻合很好,说明所采用的2D建模方法是正确的,可用于后续计算。
|
图 6 2D有限元结果和实验结果 (a)纯树脂;(b)T方向;(c)S方向 Fig. 6 Results of 2D finite element model and experiment (a) pure resin; (b) T direction; (c) S direction |
图 6(b)为T方向有限元模型模拟结果与解析结果对比,可以看出,Full模型结果与解析结果较为接近,而大于Interlamination模型。Interlamination模型与Full模型存在差距,是因为Interlamination模型考虑了实际纤维区的密度以及层间,而局部纤维密度的增加会使水的扩散路径更为复杂,扩散系数减小。对Interlamination结果进行拟合,得到扩散系数为1.86×10-3mm2·h-1,小于实验值,因而需要考虑界面对扩散的促进作用。
图 6(c)为S方向有限元模型模拟结果与解析结果对比,对有限元结果进行拟合,得到扩散系数为2.64×10-3mm2·h-1,大于T方向两个模型,说明沿层间方向对扩散系数的增加效果明显。而有限元结果远小于实验值,根据前述分析,需要考虑界面和纬纱对扩散的促进作用。
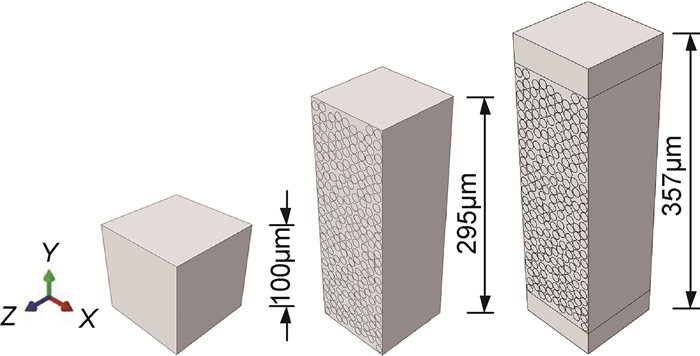
3.2 3D稳态胞元模拟 3.2.1 3D稳态胞元复合材料的扩散系数可通过其微观结构的均匀一致化获得[4]。如图 7所示,建立纯树脂、复合材料纤维区和复合材料单层的3D稳态胞元,胞元x方向和z方向尺寸均为100μm,y方向尺寸分别为100, 295, 357μm。在复合材料纤维区胞元中随机生成213根纤维。复合材料单层胞元分为上、下层间区和中部纤维区,层间区长31μm,纤维区长295μm,其纤维数量与分布和复合材料纤维区胞元一致。根据文献[19],单胞模型中纤维数量超过30根时模型有较好的代表性,本模型满足要求。将胞元模型设置为稳态扩散过程。经分析,对纯树脂胞元取4μm网格尺寸进行网格划分,对复合材料胞元的纤维区、层间区分别取0.5μm和2μm尺寸进行网格划分,单元类型DC3D8。为保证胞元的连续性,需对胞元施加周期性边界条件,如式(8):

|
图 7 3D有限元模型示意图 Fig. 7 Schematic diagram of 3D finite element model |
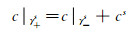
|
(8) |
式中:γ+, γ-表示相对的两个面;s表示x, y, z 3个方向;cs为该方向的浓度梯度。为方便等效扩散系数的计算,设模型3个方向均为单位浓度梯度,并将位于坐标原点的顶点浓度设置为零。编写Python脚本对模型施加上述周期性边界条件。胞元3个方向的扩散系数如式(9)所示:
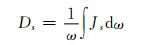
|
(9) |
式中:ω为胞元基体的体积;J表示扩散通量。
3.2.2 3D稳态模型结果3D稳态模型计算结果与三维扩散实验值对比如表 2所示,其中复合材料模型结果为取10个随机纤维分布计算的平均值。对于纯树脂胞元,其计算结果与实验值一致,说明采用三维胞元模型计算材料等效扩散系数是可行的。在不考虑界面的情况下(不建立界面层结构,但界面扩散系数与基体扩散系数的比值Di/Dm仍计为1),对于纤维区胞元,S方向和T方向扩散系数分别为1.68×10-3mm2·h-1和1.67×10-3mm2·h-1。对于层间胞元,S方向的扩散系数为2.53×10-3mm2·h-1,较纤维区胞元增加了50.6%;T方向扩散系数为1.89×10-3mm2·h-1,较纤维区胞元增加了13.2%。沿层间(S)方向的扩散系数增加更明显,是因为所增加的基体区域在S方向无纤维阻碍作用,而在T方向始终受到纤维的影响。同时,对比层间瞬态模型和稳态层间胞元,两种模型所得结果基本一致,差异为纤维分布不同所致。对于F方向,不管有无层间,其扩散系数均为3.50×10-3mm2·h-1,这是因为F方向不存在纤维阻碍作用,实际为一维扩散过程,所得结果为材料本身性能的反映。
| Model | Type | Di/Dm | DS/(mm2·h-1) | DT/(mm2·h-1) | DF/(mm2·h-1) |
| Resin | Experiment | - | 3.50×10-3 | 3.50×10-3 | 3.50×10-3 |
| FEM | - | 3.50×10-3 | 3.50×10-3 | 3.50×10-3 | |
| Composite fiber area | Non interphase | 1 | 1.68×10-3 | 1.67×10-3 | 3.50×10-3 |
| Isotropic interphase | 2.1 | 1.98×10-3 | 1.97×10-3 | 3.79×10-3 | |
| Composite layer | Experiment | - | 3.58×10-3 | 2.23×10-3 | 5.41×10-3 |
| Non interphase | 1 | 2.53×10-3 | 1.89×10-3 | 3.50×10-3 | |
| Isotropic interphase | 2.1 | 2.79×10-3 | 2.23×10-3 | 3.79×10-3 | |
| Orthotropic interphase+warp | x: 2.1; y: 2.1; z: 8.5 | 3.58×10-3 | 2.23×10-3 | 5.41×10-3 |
考虑界面对扩散的增强作用,首先假设界面是各向同性的。复合材料T方向只有界面起扩散增强作用,经计算,当Di/Dm等于2.1时,对于纤维区胞元,S方向和T方向扩散系数分别为1.98×10-3mm2·h-1和1.97×10-3mm2·h-1,说明界面对无层间纤维区的扩散增强作用是相同的;对于层间胞元,T方向扩散系数与实验值一致,因而可认为界面在该方向提供了0.34×10-3mm2·h-1的扩散作用,占该方向扩散系数的15.2%。此时S方向的扩散系数为2.79× 10-3mm2·h-1,小于实验值的3.58×10-3mm2·h-1。前述分析可知,纬纱同样提供了S方向的扩散促进作用,因此可认为纬纱增加了剩余0.79×10-3mm2·h-1的扩散作用,占S方向扩散系数的22.1%。
S方向和T方向的扩散系数均与实验值相吻合时,F方向扩散系数为3.79×10-3mm2·h-1,远小于该方向的实验值。研究表明,界面对扩散系数的作用沿纤维方向大于垂直纤维方向,因此需要考虑界面扩散系数的正交各向异性[4]。计算可得,当沿纤维方向Di/Dm的比值为8.5,垂直于纤维方向的比值为2.1时,F方向的扩散系数与实验值一致,而S方向和T方向的扩散系数保持不变。此时界面提供了1.90×10-3mm2·h-1的扩散作用,占该方向扩散系数的29.9%。
4 结论(1) 单向玻璃纤维/环氧复合材料垂直于纤维的两个方向的扩散系数不相等,这是纤维、层间、界面和纬纱的综合作用造成的。
(2) 提出的包含层间的有限元模型能较好地反应复合材料的实际结构和吸湿过程。层间对复合材料垂直于纤维方向的扩散起促进作用,且沿层间方向的促进作用大于垂直于层间方向。
(3) 纬纱对沿其方向的扩散促进作用较大。有限元模型中忽略了对垂直于纬纱方向扩散的影响,后续研究应改进。
(4) 为拟合单向复合材料的三维扩散系数,需要考虑界面沿纤维方向大于垂直纤维方向的扩散系数。
| [1] | BOND D A. Moisture diffusion in a fiber-reinforced composite part Ⅰ non-Fickian transport and the effect of fiber spatial distribution[J]. Journal of Composite Materials, 2005, 39 (23): 2113–2141. DOI: 10.1177/0021998305052030 |
| [2] | CHILALI A, ASSARAR M, ZOUARI W, et al. Effect of geometric dimensions and fibre orientation on 3D moisture diffusion in flax fibre reinforced thermoplastic and thermosetting composites[J]. Composites:Part A, 2017, 95 : 75–86. DOI: 10.1016/j.compositesa.2016.12.020 |
| [3] | JIANG X, KOLSTEIN H, BIJLAARD F, et al. Effects of hygrothermal aging on glass-fibre reinforced polymer laminates and adhesive of FRP composite bridge:Moisture diffusion characteristics[J]. Composites:Part A, 2014, 57 (1): 49–58. |
| [4] | ROCHA I B, RAIJMAEKERS S, Van Der MEER F P, et al. Combined experimental/numerical investigation of directional moisture diffusion in glass/epoxy composites[J]. Composites Science and Technology, 2017, 151 : 16–24. DOI: 10.1016/j.compscitech.2017.08.002 |
| [5] | CANAL L P, MICHAUD V. Micro-scale modeling of water diffusion in adhesive composite joints[J]. Composite Structures, 2014, 111 : 340–348. DOI: 10.1016/j.compstruct.2014.01.009 |
| [6] |
谭翔飞, 谭鹏达, 何宇廷, 等. 航空碳纤维增强树脂基复合材料加筋壁板吸湿行为[J].
材料工程, 2018, 46 (12): 61–69.
TAN X F, TAN P D, HE Y T, et al. Moisture behavior of aeronautic carbon fiber reinforced resin composite stiffened panel[J]. Journal of Materials Engineering, 2018, 46 (12): 61–69. DOI: 10.11868/j.issn.1001-4381.2017.000728 |
| [7] | SHEN C H, SPRINGER G S. Moisture absorption and desorption of composite materials[J]. Journal of Composite Materials, 1976, 10 (1): 2–20. DOI: 10.1177/002199837601000101 |
| [8] | HALPIN J C. Primer on composite materials analysis[M]. 2 Ed. Florida: CRC Press, 1992: 162. |
| [9] | GUERIBIZ D, RAHMANI M, JACQUEMIN F, et al. Homogenization of moisture diffusing behavior of composite materials with impermeable or permeable fibers-application to porous composite materials[J]. Journal of Composite Materials, 2009, 43 (12): 1391–1408. DOI: 10.1177/0021998308104229 |
| [10] |
周灿, 周储伟, 何乾强. 考虑纤维/基体界面相的复合材料湿扩散模型[J].
复合材料学报, 2014, 31 (4): 1091–1097.
ZHOU C, ZHOU C W, HE Q Q. Moisture diffusion model of composites considering fiber/matrix inter-phase[J]. Acta Materiae Compositae Sinica, 2014, 31 (4): 1091–1097. |
| [11] | WHITCOMB J, TANG X. Micromechanics of moisture diffusion in composites with impermeable fibers[J]. Journal of Composite Materials, 2002, 36 (9): 1093–1101. |
| [12] |
杨建江, 杨庆生. 纤维聚合物复合材料的有效湿扩散系数[J].
复合材料学报, 2010, 27 (4): 147–151.
YANG J J, YANG Q S. Effective moisture diffusion coefficient of fiber polymer-matrix composite[J]. Acta Materiae Compositae Sinica, 2010, 27 (4): 147–151. |
| [13] | VADDADI P, NAKAMURA T, SINGH R P, et al. Inverse analysis for transient moisture diffusion through fiber-reinforced composites[J]. Acta Materialia, 2003, 51 (1): 177–193. DOI: 10.1016/S1359-6454(02)00390-7 |
| [14] | JOLIFF Y, BELEC L, CHAILAN J F. Modified water diffusion kinetics in an unidirectional glass/fibre composite due to the interphase area:experimental, analytical and numerical approach[J]. Composite Structures, 2013, 97 (2): 296–303. |
| [15] | MENG M, RIZVI M J, LE H R, et al. Multi-scale modelling of moisture diffusion coupled with stress distribution in CFRP laminated composites[J]. Composite Structures, 2016, 138 : 295–304. DOI: 10.1016/j.compstruct.2015.11.028 |
| [16] | HAYES B S, GAMMON L M. Optical microscopy of fiber reinforced composites[M]. Materials Park, Ohio: ASM International, 2010. |
| [17] | CRANK J. The mathematics of diffusion[M]. 2 Ed. London: Clarendon Press, 1975: 47-51. |
| [18] | GAGANI A, FAN Y, MULIANA A, et al. Micromechanical modeling of anisotropic water diffusion in glass fiber epoxy reinforced composites[J]. Journal of Composite Materials, 2018, 52 (17): 2321–2335. DOI: 10.1177/0021998317744649 |
| [19] | YANG L, YAN Y, LIU Y, et al. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression[J]. Composites Science & Technology, 2012, 72 (15): 1818–1825. |
 2019, Vol. 47
2019, Vol. 47


