文章信息
- 刘培生, 杨春艳, 程伟
- LIU Pei-sheng, YANG Chun-yan, CHENG Wei
- 多孔材料性能模型研究3:数理推演
- Study on property model for porous materials 3: mathematical deduction
- 材料工程, 2019, 47(8): 59-81
- Journal of Materials Engineering, 2019, 47(8): 59-81.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2018.001412
-
文章历史
- 收稿日期: 2018-12-04
- 修订日期: 2019-04-26
多孔材料具有体密度小、比表面积大、能量吸收性好、比强度和刚度高等特点,通孔结构的多孔制品还有吸声性能佳、透过性/渗透性优良等属性[1-10]。泡沫金属是一种重要的多孔材料,具有优异的物理和力学综合性能,工程应用广泛[11-21]。不同参量和指标的泡沫金属可以适应于不同的功能用途和结构用途,且很多时候是同时担负着结构和功能的双重应用。三维网状泡沫金属可制作各种过滤器、换热器、散热器、阻燃器、多孔电极基体、高效催化剂及其载体、人工植入材料、电磁屏蔽器件等,在科学技术和国民经济建设中发挥着重要的作用[8-9, 13-21]。
文献[22]从实际应用的角度出发,指出了三维网状多孔材料的重要地位,并基于其形态特征建立了相应的简化结构模型,即源于体心立方晶格结构方式的多孔材料八面体结构模型[23]。相对于其他结构模型,该八面体模型具备自身特有的优势,其孔隙结构单元不但可以完全充满空间,即实现孔隙单元的密堆积,而且孔隙单元中的每条孔棱在结构上是等价的。但特别要注意,模型中的单元八面体并不是正八面体,而且八面体孔隙单元只包含8条孔棱而不是12条孔棱(虽然八面体有12条棱边,但本八面体模型只有其中8条组成孔隙单元的孔棱,另有相互正交的4条则不然)。在该结构模型的基础上,可进一步建立此类材料的物理、力学性能分析模型,并由此推演得出系列的相关数理关系。经工程材料实验证明,所得数理关系的理论计算具有良好的实践性[24]。
1 多孔材料的电阻率对于结构均匀、三维同性的网状多孔材料,可构建其简化结构模型(八面体结构模型)[23]:高孔率网状多孔材料系由其内部孔棱按立方体对角线的方式连接,构成大量体心立方晶格式的八面体孔隙单元。这些单元八面体在相互垂直的3个正交方向上交互紧密堆积,整齐密堆积的单元八面体在3个正交方向上规则地向外延伸,其集合即形成孔隙结构均匀的三维同性多孔体。这种结构方式下的多孔体内部所有孔棱在结构上都是等价的,所有连接孔棱的结点也都是等价的。因此,本模型体现了三维同性网状多孔泡沫材料的结构特征。从该几何结构模型出发,在此基础上赋予一定的物理意义,即可建立对应的性能分析模型。通过相应的分析推演,可进一步导出其不同物理、力学性能指标的对应数理关系规律。
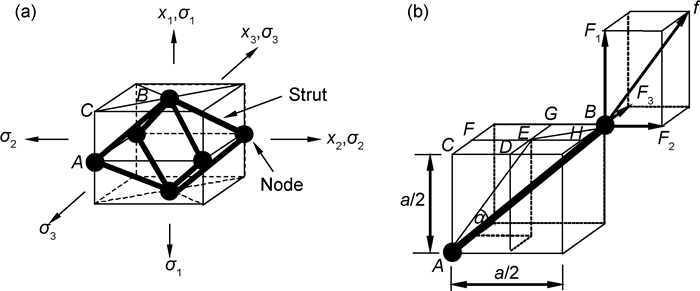
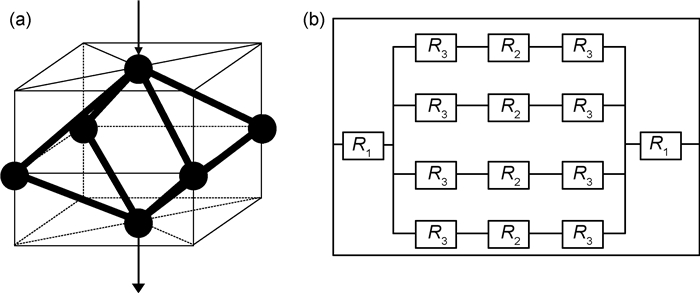
1.1 电阻率分析模型根据八面体模型的结构方式,网状多孔材料(如泡沫镍)可抽象简化为大量正交密堆积的体心立方晶格式八面体孔隙单元集合结构,其分析模型如图 1所示。设定某方向上的八面体孔隙单元轴线与多孔体整体电流方向一致,如图 1(a)所示主单元八面体中的箭头方向[25-26]。整个导电多孔体即为大量包容单元八面体的立方格子所构成的密堆积。从多孔体中隔离出一个立方格子,即可代表性地推演出整个多孔体的电阻率。
|
图 1 网状多孔材料电阻率分析模型 (a)立方格子导电单元;(b)导电单元等效电路 Fig. 1 Electrical resistivity analysis model of reticulated porous materials (a)cubic lattice of electrical conduction unit; (b)equivalent circuit of the conduction unit |
在对应的分析处理过程中,每个立方格子中单元八面体的8条孔棱均由该单元八面体独享(即不与其他立方格子中的单元八面体共用),2个顶结点(图 1(a)中所示的上下2个实心圆球)各自与处于该立方格子之上和之下的另外1个立方格子中的单元八面体所共用,4个侧结点(图 1(a)中八面体水平对称面内的4个实心圆球)则各自分别与处于该立方格子周围的另外3个立方格子中的单元八面体所共用。而且,在所有立方格子中的单元八面体都等价的基础上,不但每个立方格子中单元八面体的8条孔棱的结构状态等价,同时其8条孔棱的导电状态也是等价的。类似地,每个单元八面体的2个顶结点的结构状态和导电状态分别等价,4个侧结点的结构状态和导电状态也是等价的。所以,可以从多孔体中隔离出一个包容这样单元八面体的立方格子作为导电单元,就可代表整个多孔体进行其导电性能分析。根据以上所述,拆分该导电单元的各个组成部分,即可分析其中的电流电路:进入导电单元的电流,首先从导电单元中八面体的上顶点流入,然后均匀分布成沿着其上半部4条棱的4路分电流;这4路分电流经过八面体水平对称面上的4个侧结点流入下半部的4条棱,最后汇入八面体的下顶点流出该导电单元,于是得到图 1(b)所示的导电单元等效电路,其中R1为半顶点电阻,R2为1/4侧点电阻,R3为棱电阻。
1.2 数理关系推演为便于分析,先假定构成多孔体的孔棱形状为圆柱状。如果孔棱是中空的,则假定其中空形状亦为圆柱状。由这些孔棱相互连接形成的孔隙单元相互贯通,占据整个多孔体的主要空间,这样的孔隙定义为主孔。多孔体中所有孔隙占据多孔体整体空间的比例为总孔率(θ);主孔占有空间与多孔体整体占有空间两者的比例叫主孔率(θ′);孔棱中空占有空间与多孔体整体占有空间两者的比例为中空孔率(θ″)。于是有:θ = θ′+θ″,其中θ′≫θ″,θ′≈ θ。用几何方法配合有关电学概念对单元八面体进行等效电路近似计算和推导。
1.2.1 单元八面体有关尺寸计算 1.2.1.1 棱长(L)在八面体单元的几何模型中,8条等值边的长度L0为:

|
(1-1) |
式中a为立方格子边长。
棱长应在边长的基础上扣除结点尺度因素:

|
(1-2) |
式中L′0为结点占用尺度,相对L0来说一般很小,即通常有L≈ L0。
1.2.1.2 棱径(r)从模型结构可看出, 每个边长为a的立方体包容一个单元八面体。对于孔率较高(如70%以上)的多孔体, 主孔率与主孔体积之比等于孔棱(含内部中空)含有率与孔棱体积之比,即:
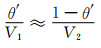
|
(1-3) |
式中:V1为主孔体积;V2为孔棱(含内部中空)体积。
式(1-3)结合图 1中的几何关系得:
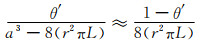
|
(1-4) |
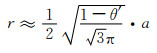
|
(1-5) |
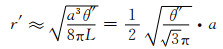
|
(1-6) |
由式(1-5)和式(1-6), 有:
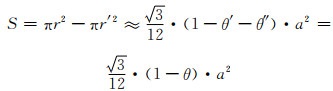
|
(1-7) |
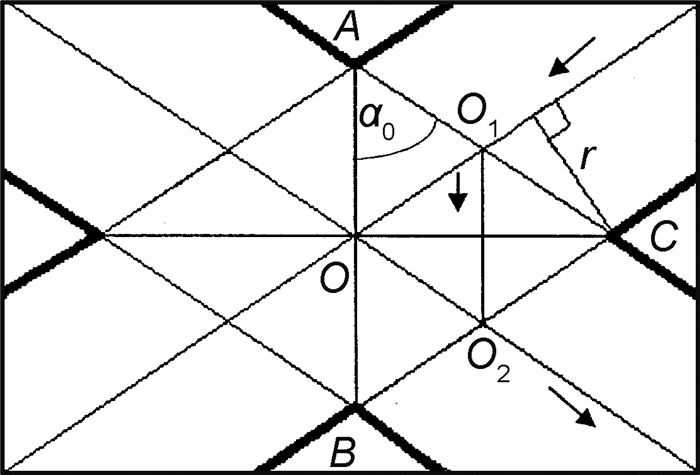
参考结点纵向剖面图(见图 2, 该图是经图 1(a)中过对称于八面体单元中心对称轴的两棱轴线之平面剖开结点而成),为标注清晰,图内未画出中空。由几何三角形相似性原理, 并考虑到实际工艺情况下材料结点的圆整作用, 结合式(1-2)和式(1-5)近似得出结点外径(R):
|
图 2 电流分析用结点纵向剖面图 Fig. 2 Sectional diagram of the node for electrical current analysis |
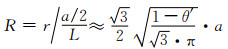
|
(1-8) |
同理, 结合式(1-2)和式(1-6),可近似得结点内径即结点中空半径(R′):
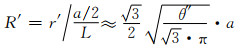
|
(1-9) |
故结点截面的有效面积为:

|
(1-10) |
根据物理量的性质,导电单元的电阻率即是整个多孔体的电阻率。设总电流方向与导电单元中的八面体轴向(即图 1(a)中箭头方向和图 2中A→B方向)相同,按照近捷传导原则, 相邻棱之间的电流走向如图 2箭头所示。对于一个导电单元来说, 电流经过其包容的单元八面体的上下顶点各半段结点、8棱4路、以及4个1/4纵分侧结点,则由图 1(b)的导电单元中单元八面体等效电路即可导出对应的电阻率。
图 2结合图 1(a)的三角形相似关系和式(1-2),(1-5), 得各棱电流流过侧结点的平均路径长度:

|
(-11) |
式中α0是单元八面体中孔棱与中心对称轴的夹角。
扣除结点路径后电流流经各棱的路径长度(L′)为:
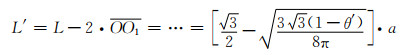
|
(1-12) |
设对应致密材质的电阻率为ρ0, 结合式(1-7),(1-10),(1-11)和式(1-12), 近似有如下R1, R2, R3。
1.2.2.1 半顶点电阻(R1)

|
(1-13) |
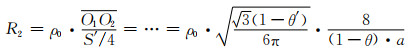
|
(1-14) |
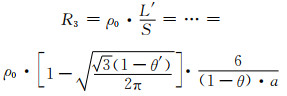
|
(1-15) |
因此, 单元八面体的总电阻(R)为:
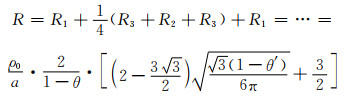
|
(1-16) |
一个单元八面体在多孔体中所占空间是体积为a3的立方体, 设其表观电阻率为ρ, 则:
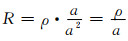
|
(1-17) |
由式(1-16)和式(1-17)可得:
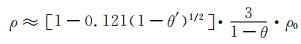
|
(1-18) |
当孔棱为实心或其内部中空孔率比主孔率小得多时, 即θ′=θ或θ′≈θ (对一般高孔率网状泡沫材料均可粗略地认为θ′≈θ), 式(1-18)简化为:

|
(1-19) |
式(1-19)是在建立分析模型中假设的理想状态下推导出来的,即推导以假设状态的规则结构为前提。由于多孔体的材质种类和实际制备工艺条件各不相同, 导致孔棱的细观结构形态(包括表面状态和内部组织结构等)、结构均匀性、连接方式和连接均匀性以及结点的细观形态、过渡方式等状态各异, 各有自身具体的特点。模型推导则未考虑实际状态的复杂性对电阻率性能的影响。这些因素都可能会造成所得数理关系表征公式对实际多孔材料的一定偏离。而且,ρ0依赖于孔棱材质的组织结构,因此也直接关联到多孔体的具体制备工艺参量。
因此,若要更精确地表征多孔材料的电阻率,可用一个表征多孔体的材质种类和具体制备工艺条件的系数K加以修正,该修正系数反映了不同多孔材料产品各自的具体结构形式, 以及内部材质的细观组织结构因素。通过系数相乘方式进行修正后为:

|
(1-20) |
其实,多孔体制品自身的具体结构状态受制于其材质种类和制备工艺条件,不但随制备工艺条件不同而变化,而且在制备工艺条件相同时也可能会随材质种类不同而改变。因此,K取决于材质种类和制备工艺条件,也就是取决于多孔体具体结构状态。可以看出,该系数同时也将多孔制品对应致密材质的电阻率ρ0修正纳入其中。
当多孔材料各向异性时, 可视分析模型中原单元八面体轴向被拉长、压扁或歪扭。从模型假设和推导过程可知, 此时各棱的分电流路径基本不变, 即单元八面体的总电阻不变, 但流经单元八面体空间的表观总电流路程和截面积均发生了变化。由式(1-17)可知, 单元八面体的表观电阻率ρ也会随之改变, 这种变化效果最终也可纳入式(1-20)的K值中。所以, 应用于各向异性的多孔材料时, 其K值还与取向有关。在式(1-18),(1-19)中,前者对应于多孔体中孔棱内部中空所占体积不能忽略的情况;后者对应于多孔体中孔棱内部中空所占体积可以忽略的情况,这是实际多孔材料呈现的一般情形。上述公式适用于高孔率范围, 对应于目前大规模生产和广泛应用的泡沫金属多孔电极材料等高孔率多孔材料产品。
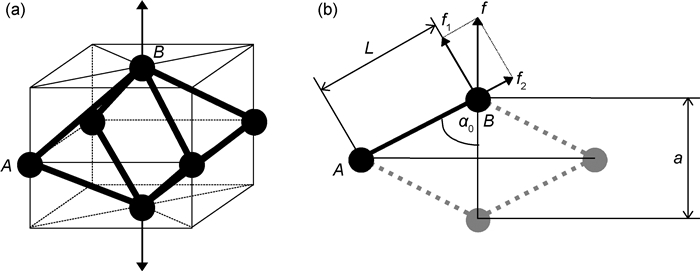
2 多孔材料抗拉强度 2.1 抗拉强度分析模型图 3为网状多孔材料抗拉强度分析模型。基于八面体结构模型,在分析多孔体的单向拉伸性能时,仅考虑轴线方向与多孔体整体受力方向一致的八面体孔隙单元,如图 3(a)所示(箭头方向为多孔体的拉伸方向),即单元八面体的轴线方向就是多孔体整体的拉伸方向[26-27]。此时整个多孔体可视为由大量包容受力单元八面体的立方格子密堆积而成,这些立方格子的结构形态相同,受力状态基本一致。
|
图 3 网状多孔材料抗拉强度分析模型 (a)包容承载主单元八面体的立方格子单元;(b)承载单元中的孔棱受力分析图 Fig. 3 Tensile strength analysis model for reticulated porous materials (a)cubic lattice containing the unit octahedron that is loading; (b)force analysis diagram for pore strut in the loading unit |
在立方格子中,不但单元八面体的8条孔棱的结构状态等价,同时其8条孔棱的承载受力状态也等价。所以,从多孔体中隔离出一个包容单元八面体的立方格子作为承载单元,然后从该承载单元中隔离出其中一条孔棱(图 3(b)中的孔棱AB,其中A和B分别为该孔棱的侧结点和顶结点)来进行受力分析,即可推演多孔体的抗拉强度数理表征。图 3(b)为孔棱受力分析图,该平面图由单元八面体中相对的4条孔棱所组成:f为承载单元所受拉伸力F分配到本单元内每条孔棱上的力,均匀分布有F=4f;f1为f在垂直于该孔棱方向上的分力,f2为f在该孔棱轴线上的分力。由于生产工艺过程对产品结构具有圆整作用,多孔体中的固体孔棱在汇合结点处的承载能力一般大于其孔棱本身,故失效破坏一般发生在孔棱上。将构成高孔率网状多孔材料的孔棱视为细梁,则当多孔体承受拉压载荷,其承载单元所受载荷导致其孔棱上任何位置的最大正应力达到对应致密材质的许用应力时,孔棱就会发生失效和破坏。大量这种同等孔隙单元中的等价孔棱的失效破坏,即可导致整个多孔体的失效和破坏。此时整个多孔体所受外加载荷所致名义拉应力即为该多孔材料的表观抗拉强度。
2.2 数理关系推演单元八面体排列规则、分布均匀,故在受到外加载荷时,多孔体内部单元八面体受力也相对均匀(在静态和准静态加载条件下,可以先不考虑多孔体开始受力时其表层可能出现的应力梯度变化较大的孔隙单元,对于脆性或高模量材质多孔体更是如此)。
参照图 3,设外加载荷施加于多孔体所致名义拉应力为σ,则八面体承载单元所受载荷F为:

|
(2-1) |
承载单元受到载荷F作用而均匀分布到其中的每条孔棱上(参见图 3(b)中的AB棱),因此孔棱所受作用力f即为:
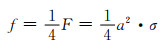
|
(2-2) |
脆性材料一般具有较高的弹性模量,受到外加载荷作用后变形量很小,几乎不产生塑性变形,直到破坏。在拉伸载荷作用下,脆性材料将不发生屈服而直接断裂。在此过程中其变形很小,可近似视为刚体。其强度失效对应于断裂,强度失效应力对应于强度极限(抗拉强度)。因此可利用弹性力学进行相关推演。
韧性材料(塑性材料)的弹性模量有高有低,其中的高模量韧性材料在拉伸过程中到达屈服时的变形也会很小,其产生屈服性强度失效的失效应力对应于屈服强度,继而达到断裂时对应于强度极限即抗拉强度。另外,比例极限、弹性极限和屈服强度三者一般非常接近,工程设计上可视其相等。因此也可借用弹性力学进行相关推演。
在外加载荷作用下,脆性材质的网状多孔体孔棱直到破坏都基本不会产生变形和位移,高模量韧性材质的网状多孔体孔棱在到达屈服前只可能会有很小的变形和位移。所以,可以将这两种情形下的泡沫材料都近似地作为刚性框架来处理,其中的孔棱视为刚体。当然,高模量韧性材质多孔体孔棱在进入屈服后达到强度极限而发生断裂的过程中,孔棱结点还可形成塑性铰,孔棱会由此产生塑性偏转,导致整个多孔框架的变形。但如果在这种情况下仅把孔棱断裂前的一旦越过弹性极限而刚刚开始屈服即视为失效,则上述刚体模型仍然适用。从弹性极限近似等于屈服应力来考虑,同样可以视弹性极限为边界条件,由弹性区推演屈服失效。
首先在刚体模型和脆性破坏的前提下,进行如下推演。对于多孔体中每条孔棱的受力分析来说,都可以简单地考虑其所受外加载荷作用在其上下两个结点,并将孔棱视为侧结点A处固定(固定端)而顶结点B处受外加载荷作用(加载端)的悬臂梁,然后运用弹性力学有关理论进行近似计算。
参考图 3及式(2-2),得出f的两个分力f1, f2分别为:

|
(2-3) |

|
(2-4) |
理论上,均匀悬臂梁产生最大弯矩的截面应在固定端根部,而实际孔棱并不均匀,破坏往往发生在较薄弱的部位,如孔棱横截面积最小的部位。这在孔棱上的任何位置(图 3中A→B之间)都有可能,但实际情况下一般出现在孔棱中部。为便于计算,避免孔棱悬臂梁受弯矩作用的力臂不确定性,先假定失效破坏发生在孔棱的中间部位,由此造成的计算偏差由修正系数进行修正。此修正系数应与实际孔棱的轴向均匀性等结构因素直接关联,因此将依赖于多孔体材质和制备工艺条件。于是,由式(1-2)和式(2-3),孔棱优先断裂部位的弯矩Mmax可近似表示为:
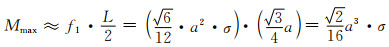
|
(2-5) |
结合式(1-5)和式(1-6)可得孔棱优先断裂部位的弯曲截面模量(W):
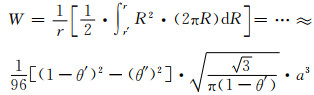
|
(2-6) |
由式(2-5)和式(2-6)可推出Mmax引起的最大正应力(σ1):
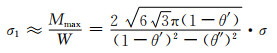
|
(2-7) |
参考式(1-5),(1-7)和式(2-4),得出由f2产生的拉应力(σ2):
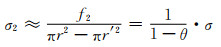
|
(2-8) |
结合式(2-7)和式(2-8)可得孔棱上产生的最大正应力(σmax):
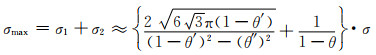
|
(2-9) |
当σmax达到相应的许用应力[σ]时,σ即对应于多孔体整体的抗拉强度,故:

|
(2-10) |
式中[σ]决定于孔棱材质的组织结构,因而与多孔体的材质种类和具体制备条件都有关。脆性材质的[σ]可直接使用其抗拉强度σ0。
式(2-10)是以假设状态的规则结构为前提进行推导的,未考虑拉伸过程中孔棱的任何形变和位移、多孔材料整体结构的规则性和均匀性、孔棱本身的均匀性(如其横截面沿长度方向有变化,包括形状和尺寸等)、多孔材料实际状态的细微构造和缺陷等形态的复杂性,特别是也未考虑孔棱的实际形状。例如,电沉积泡沫镍的孔棱为近似三棱柱状(类三棱柱状),由此在多孔体拉伸过程中呈现出来的实际截面惯性矩及对应的弯曲截面模量,将明显不同于简化推导中将其视为圆柱形所得出的截面惯性矩及对应的弯曲截面模量。因为这些因素主要受多孔材料的实际工艺状况影响,故式(2-10)用表征多孔材料材质种类和制备工艺条件的常数K′加以修正。当θ″=0或可视为足够小时,有或近似有:θ′=θ,(1-θ′)=(1-θ),(θ″)2=0,此时运用系数相乘法修正可得:
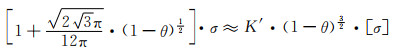
|
(2-11) |
当θ大于70%时,则为:
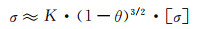
|
(2-12) |
式中
K′和K的决定因素是多孔制品自身的结构状态。该结构状态不仅取决于制备工艺条件,而且相同制备工艺条件下也可随材质种类不同而不同。
式(2-12)表明,对于脆性材质多孔体,在孔棱上任何位置产生的最大正应力达到对应密实材质抗拉强度时(即此时的许用应力可由抗拉强度代替),都会导致多孔体整体破坏的断裂出现,此时整个多孔体的名义拉应力即为该多孔材料的表观抗拉强度。
2.2.2 变形体结构受力模型在多孔体受拉伸力时,其承载孔隙单元中的孔棱与拉伸方向的夹角有减小的趋势,而且孔棱本身还存在弯曲变形的趋势,另外可能还有孔棱自身轴向的少许拉伸变形。对于弹性模量不够高的韧性材料,多孔体在拉伸过程中越过弹性极限后到达屈服时会产生较明显的变形。而且,当孔棱进入屈服到最终拉断过程中,孔棱结点会形成塑性铰,孔棱发生绕着该塑性铰的偏转,其偏转程度乃至整个多孔体的变形程度都取决于材质的韧性和塑性。韧性越大,塑性越高,孔棱的偏转度越大,高塑性材质的孔棱最终会将其轴线偏转到与多孔体拉伸方向趋于一致。
观察具有一定塑性的多孔材料的拉伸,可发现随拉伸力逐渐增大,多孔体内部孔棱与拉伸方向的夹角逐渐减小,即单元八面体被逐渐拉长。当孔棱内部产生的最大应力达到对应密实体的许用屈服应力时,孔棱也随之偏转到与之对应的某一极限位置而屈服,最后失效破坏。在此过程中,孔棱偏转效应是主要的,而孔棱本身的弯曲变形则可以纳入其“偏转程度”中一并考虑,因而两种效应可统一归结于由材质决定的偏转极限。因此,孔棱本身的弯曲变形效应对相关数理关系的影响,可以通过作为修正系数的材料常数来解决。
对应图 3(b),此时f1和f2为:

|
(2-13) |
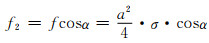
|
(2-14) |
式中:α为孔棱达到偏转极限而失效破坏时与多孔体外加拉伸力的夹角,是由材质而定的特征偏转极限夹角,且有0<α<α0;σ是发生失效时的多孔体所受外加载荷所致名义拉应力。
如准刚体结构受力模型中,将孔棱一旦越过弹性极限而进入屈服即视为失效,即可以弹性极限为边界条件,由弹性区推演失效时的力学关系。此时仍可将孔棱作悬臂梁处理(参见图 3(b)中的AB棱),借助弹性力学近似计算,并假定孔棱在转动过程中截面状态不发生变化或变化可以忽略。
结合式(1-2)和式(2-13),可得f1对孔棱失效处(孔棱中部)产生的弯矩Mmax:
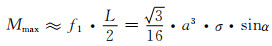
|
(2-15) |
故由式(2-15)和式(2-6)可近似得到Mmax引起的孔棱正应力σ1:
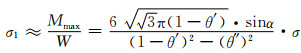
|
(2-16) |
结合式(1-5),(1-7)和式(2-14),可得f2对孔棱失效面产生的σ2:

|
(2-17) |
由式(2-16)和式(2-17)即可得出孔棱上产生的最大正应力σmax为:

|
(2-18) |
当σmax=[σ]时,式(2-18)中的σ即对应于多孔体整体的抗拉强度。同准刚体结构受力模型进行修正和处理,则当θ″=0或可视为足够小时可近似得到多孔体的σ为:
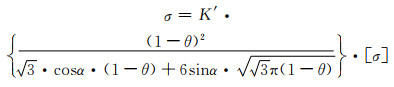
|
(2-19) |
式中α是孔棱发生塑性偏转的程度,其数值取决于材质的塑性大小,故同样可视为一个材料常数。
当多孔体为韧性大的高塑性材质时,孔棱将偏转到趋于多孔体的拉伸方向,此时α→0,因此sinα→0,cosα→1,于是式(2-19)可简化为:
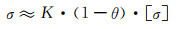
|
(2-20) |
式中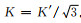
当多孔体为刚性大的低塑性材质时,孔棱几乎不发生偏转,此时α→α0,于是式(2-19)可简化为式(2-12)的形式。
比较式(2-20)和式(2-12)可知,两种极端情形的区别仅在于(1-θ)项的指数不同。于是,认为材质塑性介于这两者之间的多孔材料,其抗拉强度也可以具有类似的表述,只是(1-θ)项的指数会根据材质塑性的不同而发生变化。因此,可以将一般性网状多孔材料的表观抗拉强度近似地表示为:

|
(2-21) |
式中指数项m是多孔体对应致密材质的塑性指标,其值介于1和1.5之间。对应材质的脆性越大、刚性越高,则m偏向于1.5;对应材质的韧性越大、塑性越高,则m偏向于1;而当对应材质为塑性适中的一般金属或合金时,可近似取其中值,即m≈1.25。
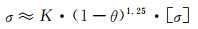
|
(2-22) |
无论是韧性大的高塑性材质(极限情况为孔棱偏转到垂直于多孔体的压缩方向),还是刚性大的低塑性材质(极限情况为孔棱构成结构稳定的框架),都可以得到形式同于式(2-12)的多孔材料表观压缩强度表征关系。由此认为,材质塑性介于两者之间的一般性网状多孔材料,其表观压缩强度也都可近似地表示为:
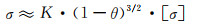
|
(2-23) |
三维网状泡沫金属的宏观断裂方式与传统理论的金属体在受力方向拉断不同,而是内部众多金属棱体的“撕断”,颈缩影响也很小[28-29]。本理论正是针对高孔率材料结构和断裂方式的特点,运用简化的几何模型,采取宏观力学分析方法,建立起“弯矩→最大应力→撕裂”的高孔率材料拉伸破坏模式,最终得出对应的计算公式。当然,正如相关领域专家所指出,多孔材料的实际发生破坏是一个演变过程,如其内部孔棱受压后会形成与受压方向接近45°的一个或多个微小剪切破坏带,这些微小破坏带的进一步演化诱导最终的多孔体宏观破坏发生。可见,多孔体实际破坏可能不会如本模型假设的那样直接。但是,这种模型假设带来的实际偏离问题,可通过引入修正性的材料常数而得以较好解决,文献[24]中的实验验证很好地支持了这一点。本领域普遍接受的著名经典性模型理论即Gibson-Ashby模型理论,也是基于孔棱在弯矩作用下产生的最大应力即对应于泡沫材料的失效破坏这一假设前提。工作证明[30]这种假设是可行的,该模型理论在多孔材料界被长期地广泛利用,明显推进了此类材料的研究和发展。
3 多孔材料的伸长率 3.1 伸长率分析模型在八面体孔隙单元结构模型的基础上,分析多孔体在单向拉伸载荷作用下的伸长率时,仅考虑轴线方向与多孔体整体受力方向一致的八面体孔隙单元。对孔隙单元进行拉伸分析推演,即可导出多孔体的伸长率。多孔体在拉伸期发生的塑性变形,主要是大量孔棱沿对应拉伸方向的塑性偏转,它们使多孔体在拉伸方向对应的相对伸长百分比即为伸长率[31]。
3.2 数理关系推演根据伸长率分析模型,多孔体受拉伸载荷作用时,八面体孔隙单元中的孔棱与八面体轴线间的夹角有减小的趋势。将孔棱视为侧结点A处固定而顶结点B处受载荷作用的悬臂梁,孔棱与单元八面体轴线的原夹角α0=arccos(3/3)。
工程力学和材料力学中有关悬臂梁产生的最大应力(σmax)与所受弯矩(M)及梁的弯曲截面模量(W)之间的关系为:
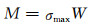
|
(3-1) |
作为悬臂梁,孔棱所受弯矩越大,其可能弯曲偏转的程度越大;而弯曲截面模量越高时,抵御弯曲偏转的能力也就越强。所以,孔棱拉伸断裂时发生的偏转角度(α0-α)(其中α是断裂时孔棱与八面体轴线的夹角)可随其能承受的极限弯矩Mmax=[σ]W增大而增大,而随其抗弯截面模量W增大而减小。因此,为演算方便,可认为(α0-α)的量值与Mmax近似成正比,而与抗弯截面模量W近似成反比,即:
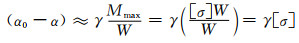
|
(3-2) |
式中γ是由材质决定的比例系数(同一工艺制备的同种材料则γ相同),可见断裂时孔棱与八面体轴线的夹角α是由材质而定的特征偏转极限夹角。
观察具有一定塑性的多孔体拉伸可发现,当拉伸力达到某一大小,孔棱内部产生的最大应力达到相应密实体抗拉强度时,孔棱随之偏转到对应的某一极限位置而断裂。
参考图 3及其结点剖面图 2,利用几何方法进行有关尺寸计算。在单元八面体中,结合图 2的几何关系及式(1-12),可得单元八面体的原孔隙高度h1(图 4(a))。

|
图 4 单元八面体所含孔隙(主孔)高度在多孔体拉伸前(a)和断裂后(b)的变化示意图 Fig. 4 Sketches of pore height in the unit octahedron before tension(a) and after rupture(b) of porous body |
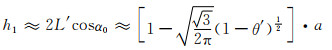
|
(3-3) |
孔棱断裂后的塑性伸长包括均匀塑变和缩颈塑变两部分,即孔棱偏转断裂后的长度L2可近似为[32]:

|
(3-4) |
式中:k1,k2为常数,当材料为纯脆性时,k1=k2=0;L1为扣除结点后的孔棱长度; S为孔棱的横截面积。对于高孔率网状泡沫金属,主要由孔棱受弯矩产生最大拉应力导致断裂,一旦孔棱一侧拉出裂口就会随即发生裂纹,并在该孔棱上迅速扩展,孔棱本身在轴向(长度方向)上的塑性拉长和颈缩均相对较小,伸长率主要取决于孔棱的塑性偏转。故k1和k2均很小,特别是k2。
由式(3-4)结合式(1-7)和式(1-12),可得单元八面体发生孔棱偏转断裂后的孔隙高度h2:
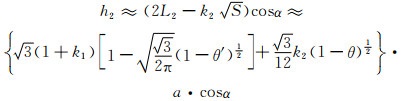
|
(3-5) |
式(3-5)减去一个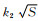

|
(3-6) |
由于结点部分的承载截面积要比孔棱的大,故其承受载荷能力也相应地比孔棱的高,因此在孔棱拉断时结点所能产生的塑性变形一般很小,相对于孔棱偏转而产生的沿拉伸方向的尺寸变化来说,其可以粗略不计。设多孔体在拉伸方向上包含有m(m≫1)个单元八面体(图 4),则结合式(3-3),(3-5)和式(3-6),可得伸长率δ为:
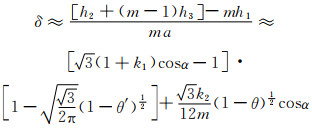
|
(3-7) |
如果起始标距足够长,即拉伸方向上包含的单元八面体数量m足够大,则式(3-7)中第二项的权重可忽略不计,多孔体断后总伸长率与原始标距关系不大,从而近似有:
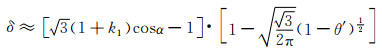
|
(3-8) |
当然,推演并没有考虑多孔体各部分弹性作用因素(弹性形变、弹性位移)带来的影响。这主要是基于两个原因:一是弹性作用因素对于孔棱的塑性偏转来说相对很小;二是样品断后接合测量时基本只剩下塑性作用因素,弹性作用因素基本消失。
当材料为脆性时,发生脆断,此时有k1 =0和cosα=
多孔材料的实际结构状况远比推导中的简化处理复杂,孔棱形状、孔隙形状、孔径分布和均匀度,以及具体的结构和缺陷方式等,都会对伸长率产生影响,而决定结构形态的因素主要在于制备工艺和材质种类,故式(3-8)应采用表征工艺影响和材质种类的系数进行修正。
对式(3-8)进行系数相乘法修正可得:
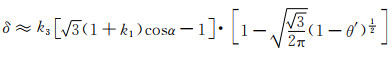
|
(3-9) |
由于α,k1和k3均是取决于多孔体材质的常数,故可设:
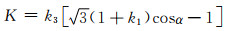
|
(3-10) |
代入式(3-9)得:

|
(3-11) |
对于一般的高孔率泡沫金属,可认为θ′≫θ″,θ′≈θ,故式(3-11)可近似写成:
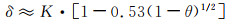
|
(3-12) |
从公式的推导过程可看到:高孔率网状多孔材料的伸长率主要取决于多孔体的材质和孔率。只要多孔体在拉伸方向上的尺寸足够大,或者所含孔隙数目足够多,在拉伸速率一定的情况下,对同一工艺制备的同种材料伸长率只受孔率因素制约。式(3-11)和式(3-12)的推导是基于各向同性、结构均匀的多孔体,而当多孔体各向异性时,可视分析模型中的单元八面体被拉长或压扁,即八面体孔棱与中心对称轴的原夹角α0发生变化,由式(3-2)可知,特征极限夹角α也会随之改变。这种改变的作用最终体现在式(3-12)的系数K上。所以,当多孔体为各向异性的泡沫材料时,K的取值除取决于制造工艺和所用材质种类外,还与被拉伸的方向有关。
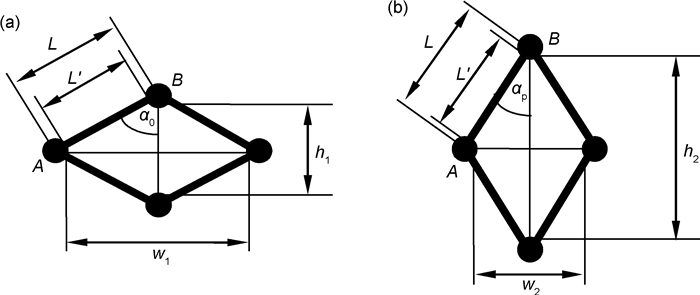
4 多孔材料弹性模量 4.1 弹性模量分析模型三维同性的均匀网状多孔材料可视为大量体心立方式八面体结构的孔隙单元集合,拉伸载荷作用下多孔体发生的变形主要源于孔棱沿多孔体拉伸方向产生的偏转(图 5)[33]。当变形使孔棱内部产生的应力达到对应致密材质的比例极限(σp)时,多孔体在拉伸方向上承受的名义应力即为表观比例极限(σ′p),多孔体的表观应变即为其表观线弹性应变极限(εlim)。表观比例极限与其在拉伸方向上的表观线弹性应变极限(εlim1)之比为表观杨氏模量(Ea),其垂直于拉伸方向的横向表观线弹性应变极限(εlim2)负值与其拉伸方向上的表观线弹性应变极限(εlim1)之比则为多孔体的表观泊松比(νa)。
当多孔体受到外加拉伸载荷时,会将受力作用传递到内部的各个孔隙单元中,图 3中的f1和f2分别对孔棱产生弯曲作用和拉伸作用。多孔体受到外加拉伸载荷后,单元八面体孔隙中的孔棱与单元轴线之间的夹角会减小或具有减小的趋势。于是,可将孔棱视为侧结点A处固定而顶结点B处受载荷作用的悬臂梁。孔隙单元在孔棱受力发生偏转前后的结构参量见图 5。图 5中h1和w1分别为孔棱发生偏转前的孔隙单元高度和宽度,h2和w2分别为孔棱受力发生偏转到失效前极限位置时孔隙单元的高度和宽度,αp为孔棱偏转到对应极限位置时与单元八面体轴线的夹角。由于孔棱发生沿着八面体孔隙单元轴线的偏转,因此其夹角在多孔体拉伸过程中逐步变小,有αp<α0。
当孔棱内部的应力达到σp时,其偏转角度Δα随Mp增大而增大,而随W增大而减小。
Δα为:
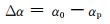
|
(4-1) |
式中0<αp<α0。又由M=σmaxW的关系有:

|
(4-2) |
为计算方便,可认为Δα量值近似与Mp成正比,而与W成反比,因此有:
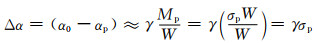
|
(4-3) |
式中γ是由多孔体的材质决定的比例系数。
观察弹塑性金属多孔体的拉伸,可发现当施加在多孔体上的拉伸力达到某一大小,孔棱内部产生的最大应力达到对应致密材质的比例极限时,孔棱也随之弹性偏转到与之对应的某一位置而向非线弹性偏转过渡。比例极限、弹性极限和屈服强度三者一般非常接近,工程设计上可视其相等,因此可将αp视为孔棱失效前的偏转极限夹角。
在单元八面体中,结合图 2的几何关系及式(1-12),可得单元八面体原孔隙高度,即式(3-3)。对应地,垂直于单元八面体高度方向的原孔隙最大尺寸为:
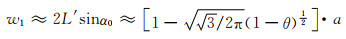
|
(4-4) |
对于高孔率网状泡沫金属,其孔棱受弯矩作用而产生偏转,孔棱本身的拉长相对较小,多孔体名义应变主要取决于孔棱的偏转。当单元八面体中的孔棱偏转到与拉伸方向的夹角为αp时,其孔隙高度变为:
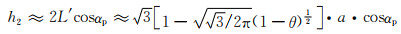
|
(4-5) |
对应地,垂直于高度方向的孔隙最大尺寸变为:
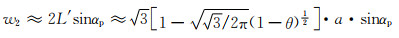
|
(4-6) |
因此,多孔体在拉伸方向和垂直于拉伸方向的表观线弹性应变极限分别为:
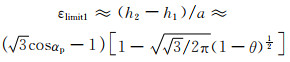
|
(4-7) |
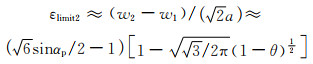
|
(4-8) |
由式(4-7)和式(4-8)可得多孔体的表观泊松比:
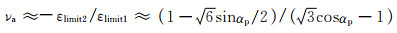
|
(4-9) |
令:
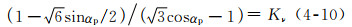
|
(4-10) |
则:

|
(4-11) |
式中Kν是取决于多孔体材质的常数。由此可知,表观泊松比也是对应于多孔体材质的材料常数,与其孔率无关。
上述推导过程以三维各向同性、结构均匀的多孔体为前提,对于各向异性的多孔体,则可视分析模型中的原单元八面体被拉长或压扁,即孔隙单元中的孔棱与八面体中心对称轴的原夹角α0发生改变。于是,式(4-1),(4-3)以及式(4-7),(4-8)的值也都随之变化,而且这种变化的作用最终落于式(4-9),(4-10)。因此,当多孔体为各向异性的泡沫材料时,Kν取值除受制于材质种类和制备工艺外,还与方向有关。
另外,按照类同于本文关于抗拉强度推演过程的方法,可得多孔体表观比例极限:

|
(4-12) |
根据式(4-7),(4-12),可得多孔体的表观杨氏模量为:

|
(4-13) |
令:

|
(4-14) |
得:
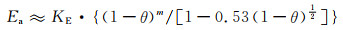
|
(4-15) |
参照单向拉伸分析模型的构建方式,在分析多孔体的双向拉伸性能时,受力分析仅考虑轴线方向与多孔体整体受力方向一致的八面体孔隙单元[34-35],如图 6所示。由图 6(a)可知,主单元八面体的轴向是多孔体的受力方向之一,其对应名义主应力为σ1;主单元八面体左上方的副单元八面体(图中未显出)轴向是多孔体的另外一个受力方向,其对应名义主应力为σ2。孔棱AB为两个单元八面体共同作用的双重受力:既有来自主单元八面体源于σ1的作用力,又有来自副单元八面体源于σ2的作用力。对孔棱AB的受力分析而言,虽然其为3个相邻的密积八面体孔隙单元所共用,但只需考虑主单元和主单元左上方的副单元。将高孔率网状多孔材料的孔棱视为细梁,当多孔体承受拉压载荷,其承载单元所受载荷导致孔棱上任何位置的最大正应力达到对应致密材质的许用应力时,孔棱就会发生失效和破坏。大量同等孔隙单元中的等价孔棱的失效破坏,即可导致整个多孔体的失效和破坏。

|
图 6 网状多孔材料双向拉伸分析模型 (a)八面体孔隙单元; (b)孔棱 Fig. 6 Analysis models for biaxial tension of reticulated porous materials (a)octahedron unit; (b)pore strut |
对多孔体的受力分析,从其孔隙单元中的某一孔棱(如图 6中的AB棱)入手。在等价结构的单元八面体中,孔隙单元的孔棱结构状态等价,同时其承载受力状态也对应等价。由此,得到如图 6(b)所示的孔棱受力分析图。其中F1为源于σ1对多孔体的作用而分配到孔棱AB加载端B点的作用力,F2为源于σ2对多孔体的作用而分配到孔棱AB加载端B点的作用力,f为孔棱AB在加载端B点受到的合力,AD为f方向的平行线,α1为f方向与σ1方向的夹角,α2为AD与AB的夹角。
5.2.2 孔棱受力分析与关系推导关于多孔体单向拉伸的推演,对应的处理仅仅是解决本问题的一种简化分析方式。然而,此方式不但在单向拉伸分析时被证明可行,同时其可行性和合理性也得到双向拉伸进一步的相关实验结果检验[24]。单元八面体中的每一孔棱为3个八面体孔隙单元所共用。而在图 6(b)的双向拉伸受力分析中,仅考虑有轴向拉伸力的单元。其推演过程先基于孔棱的“脆性破坏”假设,且由细梁理论忽略剪切应力的影响。
参照图 6,设施加于多孔体垂直方向和水平方向上的外加载荷所致两个名义主应力分别为σ1和σ2,则对于孔棱AB的顶端B所受外力的竖向力和水平力以及合力分别为:

|
(5-1) |
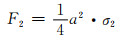
|
(5-2) |

|
(5-3) |
实际上结点作用力也会涉及弯矩,但将结点抽象为数学上的点,仅仅起到传递外力的作用。这种处理方式不会带来明显的偏差,因为此时分析系统不产生新的力,而且实际结点的承载能力一般都高于孔棱。
设合力f与σ1的夹角为α1,并且先假定σ1≠0,则由图 6结合式(5-1),(5-2),(5-3)可得:

|
(5-4) |

|
(5-5) |
过A点作合力f方向的平行线与包含八面体的立方格子的棱边交于D点(见图 6),则由式(5-4)和式(5-5)可得:
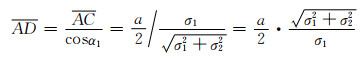
|
(5-6) |

|
(5-7) |
又
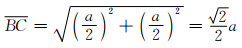
|
(5-8) |
式(5-7)和式(5-8)结合余弦定理得:
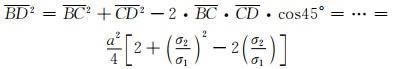
|
(5-9) |
又
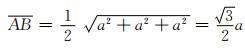
|
(5-10) |
设AD与AB的夹角为α2,则由式(5-6),(5-9),(5-10)结合余弦定理,可得:

|
(5-11) |
由此得:

|
(5-12) |
由式(5-3),(5-11)和式(5-12)结合图 6,得AB棱在端点B所受外加力的横向力和轴向力分别为:
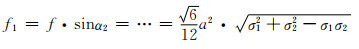
|
(5-13) |
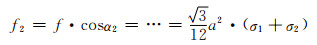
|
(5-14) |
由式(2-6)进一步简化得出W为:
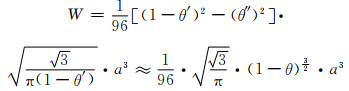
|
(5-15) |
对脆性材料运用线弹性弯曲理论,由式(5-13), (5-15)可得弯矩引起的孔棱最大正应力(σ01)为:

|
(5-16) |
由式(1-7),(5-14)可得f2产生的轴向拉应力(σ02)为:
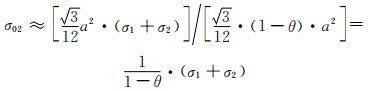
|
(5-17) |
由式(5-16),(5-17)可知,孔棱内部σmax为:

|
(5-18) |
推导虽以σ1≠0为前提,但这只是推导过程的需要,推导结果的使用并无此限制。在双向拉伸过程中,不需要另外考虑孔棱的轴向压缩。
上述推导是在理想的简化状态下进行的,而实际情况则较为复杂。因此,多孔体在双向拉伸过程中实际产生的最大应力,应该在导出的σmax基础上加以修正。类似于前述最简修正方法,是在σmax前加一表征多孔体孔棱实际结构状态的修正系数k,即实际最大应力为:

|
(5-19) |
得多孔体在双向拉伸破坏时两个名义主应力的关系:
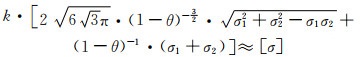
|
(5-20) |
由此得:
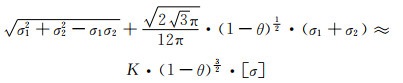
|
(5-21) |
以上推导是以脆性破坏断裂为基础的。为适应其他失效形式,沿袭和参照关于抗拉强度推演的处理过程,通过类似的方式对相关表达式中的指数项进行拓展,即得:
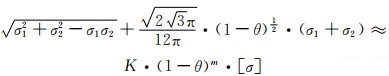
|
(5-22) |
在多孔体双向承载下,相当于在三维空间内有两个方向的载荷不为0,而第三个方向的载荷为0,如:σ1≠0,σ2≠0,σ3=0。此时借用连续介质力学中的偏应力σd(注:偏应力是指偏离静水应力并引起形变的应力,可以表征总体载荷的综合作用效应)和平均主应力σm,则有:
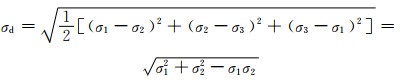
|
(5-23) |
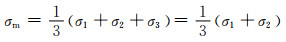
|
(5-24) |
将式(5-23)和式(5-24)代入式(5-22),得:

|
(5-25) |
式(5-25)即为通过八面体模型理论获得的用偏应力表征的多孔材料双向负载失效时的数理关系,即该材料在双向承载条件下名义失效偏应力与孔率的关系。对于本模型理论来说,式(5-25)左边第二项对多孔体承载失效的作用权重相对较小,主要是第一项偏应力的作用结果。因此,可进一步近似表达为:
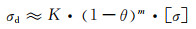
|
(5-26) |
基于式(5-22)的推导过程,可以得到与该式表达完全相同的网状多孔材料承受双向拉压载荷时的数理关系,其中只需对σ1和σ2按照拉伸应力取正号而压缩应力取负号的原则即可。但要注意,此时塑性指标m的取值问题:当多孔体所受载荷以压缩为主时,即σ1和σ2中较大的为压缩应力或两者都为压缩应力时,m通取1.5;而当多孔体所受载荷以拉伸为主时,即σ1和σ2中较大的为拉伸应力或两者都为拉伸应力时,m取值介于1~1.5之间。
6 三向拉压力学模型 6.1 三向拉压分析模型网状多孔材料三向拉伸分析模型如图 7所示[36-37]。在三向承载受力分析中,亦考虑有轴向拉伸力的单元,此时3个相互垂直方向即x1,x2和x3方向上的孔隙单元都需要考虑。如图 7所示,x1方向是主单元八面体的轴向,其对应名义主应力为σ1;x2和x3方向是多孔体的另外两个受力方向,其对应名义主应力分别为σ2和σ3。八面体孔隙单元中每一孔棱为3个八面体单元所共用。因此,对孔棱AB,需要考虑3个八面体孔隙单元共同作用其上的3重受力。将孔棱视为细梁,当多孔体承受拉压载荷,其承载单元所受载荷导致孔棱上任何位置的最大正应力达到对应致密材质的许用应力时,孔棱就会发生失效和破坏。大量这种同等孔隙单元中的等价孔棱的失效破坏,即可导致整个多孔体的失效和破坏。
在多孔体承受三向载荷作用力时,一般是某一或某两个方向的载荷为主,因此八面体孔隙单元中的孔棱也会受力而产生偏转或具有偏转的趋势。如果是韧性材质,孔棱结点会形成塑性铰,孔棱会由此产生绕着该塑性铰的塑性偏转,导致整个多孔框架的塑性变形。因此,为简化推导过程,先以多孔体三向拉伸为条件,并将孔棱作“脆性悬壁梁近似”进行受力分析。
在本分析模型中,八面体孔隙单元中所有孔棱都是对应等价的,可以从三向拉伸分析模型隔离出八面体孔隙单元中的某一条孔棱来进行代表性的受力分析(参见图 7)。沿袭双向拉伸分析模型的操作方式,来分析多孔体的三向拉伸受力状态:在分析孔棱的“悬臂梁近似”受力时,被隔离出来的孔棱AB承载端所受外加载荷,即为在双向拉伸受力分析基础上再叠加一个相邻孔隙单元(图 7中的x3方向)共用孔棱的端点受力。
6.2.2 孔棱最大正应力推导将图 7(a)中的AB棱隔离分析,并假定其为侧结点A固定而顶结点B受外加载荷作用的悬臂梁。于是,可得到如图 7(b)(该图是从图 7(a)中隔离出来的左前上方的小立方体)所示的AB棱受力分析图:其中F1为源于σ1对多孔体的作用而分配到孔棱AB加载端B点的作用力,由图 7(a)中的主单元计算;F2为源于σ2对多孔体的作用而分配到孔棱AB加载端B点的作用力,由图 7(a)中主单元左上角的副单元计算;F3为源于σ3对多孔体的作用而分配到孔棱AB加载端B点的作用力,由图 7(a)中主单元前上角的副单元计算;f为孔棱AB在加载端B点受到F1,F2和F3的合力。推演过程先基于孔棱的“脆性破坏”假设,且由细梁理论可忽略剪切应力的作用。
对于单元八面体中的孔棱AB,其顶端B在x1,x2和x3方向上所受外力分别为(参见图 7(b)):
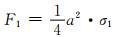
|
(6-1) |
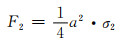
|
(6-2) |

|
(6-3) |
得f为:
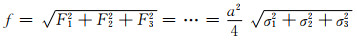
|
(6-4) |
将图 7(b)中F1,F2和F3组成的长方体向左下前方平移并放大,使平移放大后的长方体左前边恰好与AC重合,即将长方体(BF1F2F3f)平移放大为长方体(ACDEF)。该放大倍数为(假定σ1≠0):
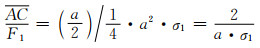
|
(6-5) |
由此得:
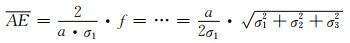
|
(6-6) |
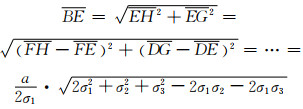
|
(6-7) |
式中:G为DE延线与立方体的后上棱边的交点;H为FE延线与立方体的右上棱边的交点。
由图 7(b),设f与AB的夹角即AE与AB的夹角为α,则结合余弦定理可得:

|
(6-8) |
由式(6-6),(6-7)和式(6-8)可得:
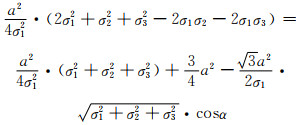
|
(6-9) |
由此得:
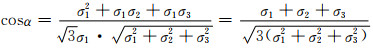
|
(6-10) |
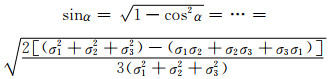
|
(6-11) |
式(6-4),(6-10)和式(6-11)结合图 7(b),得AB棱所受横向力和轴向力f1, f2分别为:
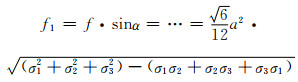
|
(6-12) |

|
(6-13) |
按照抗拉强度推演中关于孔棱悬臂梁的力臂分析方法,通过式(6-12), (5-15),得弯矩引起的孔棱最大正应力σ01为:
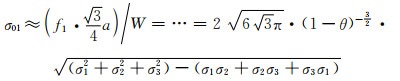
|
(6-14) |
通过式(6-13), (1-7),得孔棱轴向力产生的拉应力σ02为:
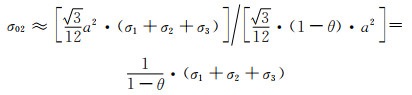
|
(6-15) |
结合式(6-14),(6-15),得孔棱内部σmax。

|
(6-16) |
上述推导为理想的简化状态,而实际多孔体的多向拉伸情况较为复杂,故最大名义应力应在σmax基础上加以修正。采用系数修正法,得实际最大名义应力为:
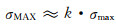
|
(6-17) |
式中的修正系数k实际上是一个大于1的材料常数,它涵盖了多孔体材质种类、孔隙结构、孔棱结构和制备工艺条件等因素的作用。当实际泡沫体的孔棱内部组织结构偏离于对应致密体的理想结构,以及孔棱形状偏离于圆柱形时,k值也相应地偏离于1。
通过推导和分析,得出关于脆性材质多孔体在多向拉伸破坏时3个名义主应力与孔率的数理关系为:

|
(6-18) |
由此得:
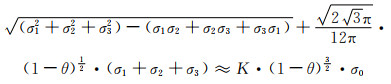
|
(6-19) |
式中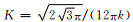
此外,上述推导基于脆性断裂。为适应更多的失效方式,进行相关表达式中的指数项拓展,得:

|
(6-20) |
可以看出,σ1,σ2,σ3三者是等价的。
6.2.4 简化表达沿袭双向拉伸推演,借用偏应力σd和平均主应力σm的概念,则可由式(6-20)得更为简单的关系表达式:

|
(6-21) |
式(6-21)即为通过本八面体模型理论获得的用偏应力表征的多孔材料三向负载失效时的数理关系,即在三向承载条件下名义失效偏应力与孔率的关系。对于本模型理论来说,左边第二项对多孔体承载失效的作用相对很小,主要是第一项偏应力的作用结果。因此,该式还可进一步近似表达为:

|
(6-22) |
比较可知,该偏应力表达形式与多孔材料单向负载和双向负载情形都是一致的,表明其力学行为在不同拉压载荷方式作用下存在某种统一的内在规律,同时也从另一侧面反映出本八面体模型理论的可行性和适应性。
6.3 三向拉压问题基于式(6-20)的推导过程,可以得到与该式表达完全相同的网状多孔材料承受三向拉压载荷时的数理关系,但其中:①当多孔体在某一方向承受拉伸载荷时,其对应所致名义主应力σi(其中i=1, 2, 3)取正号;当多孔体在某一方向承受压缩载荷时,其对应所致名义主应力σi取负号。②m取值:当多孔体所受载荷以压缩为主时,即σ1,σ2和σ3中较大的为压应力时,m通取1.5;而当多孔体所受载荷以拉伸为主时,即σ1,σ2和σ3中较大的为拉应力时,m取值方式同式(6-20),即m介于1~1.5之间,且对应高脆性致密材质m偏向取1.5,对应高塑性致密材质m偏向取1,对应塑性适中的材质近似取1.25。
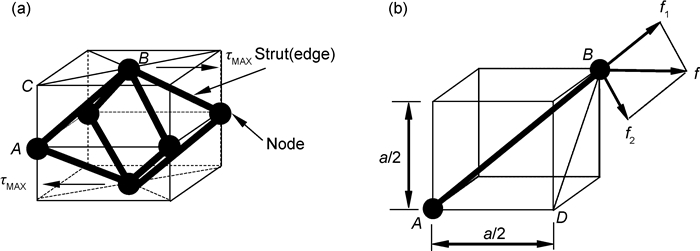
7 其他载荷形式力学模型 7.1 剪切载荷作用 7.1.1 物理模型图 8为剪切载荷作用下多孔体中孔隙单元的受力分析模型。均匀结构的三维同性网状多孔材料,可视为孔棱规则地按立方体对角线方式连接而构成的八面体孔隙单元集合(参见图 8(a)中的粗实线结构)。多孔体构件在承受剪切作用时,由构件内的最大名义切应力(τMAX,其大写下角标对应于整个多孔体)造成孔棱最大正应力σmax达到对应密实材质的许用应力时,就会萌发孔棱失效,而最终导致多孔体的整体性失效[38-39]。
|
图 8 剪切载荷作用下多孔体中孔隙单元的受力分析模型 (a)八面体单元; (b)孔棱 Fig. 8 Analysis model for pore unit of the porous body under shearing loads (a)octahedron unit; (b)pore strut |
假定多孔体构件所受剪切作用的方向如图 8(a)中的水平方向,根据工程力学和材料力学的梁理论分析,可判断出单元八面体四次对称轴的左上边2条孔棱上将会出现最大拉应力,而右上边的2条孔棱则有对等的最大压应力。因此,可将左边的AB棱隔离出来进行受力分析(参见图 8(b),该图为从图 8(a)中隔离出来的左前上方的小立方体),并假定侧结点A固定而顶结点B受外加载荷作用。如此,即可将多孔体内部所受的名义切应力作用转化为对八面体单元中孔棱的牛顿力(注:本文用此术语特指以牛顿为单位的力,以区分于本节的“切应力”以及后面的“扭矩”和“弯矩”等构件内力分量)作用,而不考虑名义切应力直接对孔棱的剪切破坏作用。推演过程先基于孔棱的“脆性破坏”假设,且由细梁理论可忽略孔棱中剪切应力的作用。
在图 8所示的承载情况下,孔棱AB顶端B所受外力大小为:
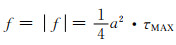
|
(7-1) |
该力水平向右,是由八面体单元的名义切应力作用而转化成的对孔棱顶端的牛顿力作用。
在图 8(b)中,f为作用在孔棱顶端的牛顿力,将其正交分解为两个相互垂直方向上的分力f1和f2,其中f1处于AB的延长线上,而f2则垂直于AB的轴线。由此根据图形的几何分析还可知,∠BAD与∠f1Bf相等,设

|
(7-2) |
则

|
(7-3) |
由此得:

|
(7-4) |

|
(7-5) |
结合式(1-7),则由式(7-4)可得孔棱的轴力所致拉应力σ01为:
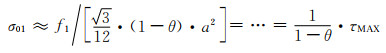
|
(7-6) |
式(5-15)结合式(7-5),得孔棱的弯矩所致正应力σ02为:
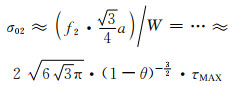
|
(7-7) |
结合式(7-6)和式(7-7),并考虑到σ01和σ02在拉伸时取正号,而在压缩时取负号,可得孔棱内部最大正应力σmax为:
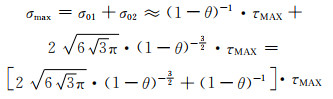
|
(7-8) |
多孔体承受剪切作用,σmax≥[σ],亦即:

|
(7-9) |
多孔体将会萌生整体性失效。
7.1.4 数理关系修正上述推导和分析为理想的简化状态,因此对应孔棱内部实际出现的最大拉应力,应在理论导出的σmax的基础上加以修正。采用系数修正法,进行相关表达式中的指数项拓展,得出多孔体构件在剪切载荷作用下发生失效时最大名义切应力与孔率的数理关系为:

|
(7-10) |
另外,根据式(7-10),可将式(7-9)进一步表达为:
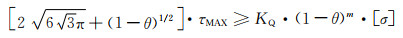
|
(7-11) |
多孔体构件在承受扭转载荷时,由名义扭矩T导致的孔棱最大拉应力σmax达到对应密实材质的许用应力时,就会萌发多孔体的整体性失效[40]。
7.2.2 数理推演 7.2.2.1 最大拉应力假定作用在多孔体构件上的扭矩矢量处于竖直方向,由此而导致的剪切作用则为水平方向,设切应力方向为图 8(a)中所示的水平方向。取扭矩导致最大剪切作用处的八面体单元为研究对象。根据梁理论分析判定图 8(a)单元八面体中的左上侧2条孔棱上将会出现最大拉应力,因而一般会优先发生失效和破坏。因此,可将孔棱AB隔离出来进行受力分析(参见图 8(b))。如此,即将多孔体内部所受扭矩作用转化为对八面体单元中孔棱的牛顿力作用,而不考虑扭矩直接对孔棱引起的剪切破坏作用。
根据工程力学和材料力学可知,在受到扭矩T作用时,无论构件截面为何种形状,产生的最大名义切应力为:
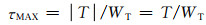
|
(7-12) |
式中:WT为取决于多孔体构件截面几何因素的常量。对于圆形截面通常称为扭转截面模量(抗扭截面系数),表示为WP。
根据与剪切推演部分完全相似的推演,可得到与式(7-8)同样的结果,只需将式(7-8)中的τMAX代之以式(7-12),即可得:

|
(7-13) |
借助圆轴扭转时的应力状态,分析多孔体承受扭转载荷时的危险位置孔隙单元受力情况。图 9为受到外部扭转力偶(Me)作用的圆轴及其孔隙单元受力分析模型。圆轴受扭发生变形后其横截面保持平面,并绕圆轴轴线刚性地转过一个角度。因此,圆轴在扭转变形后,其圆周线将从原来的位置(参见图 9(a)中的AB和CD)平移至新的位置(参见图 9(b)中的A′B′和C′D′),而其圆柱面母线则从原位置(参见图 9(a)中的AC和BD)转动到新位置(参见图 9(b)中的A′C′和B′D′),转动的角度(参见图 9(c)中右边的γ)对应于分析微元(参见图 9(c)中的ABCD)的切应变[41]。

|
图 9 多孔体圆轴扭转变形及其孔隙单元受力分析模型 (a)未变形的圆轴[41]; (b)变形后的圆轴[41]; (c)圆轴切应力分析单元[41]; (d)孔隙单元受力分析模型 Fig. 9 Torsional deformation of the porous shaft and the force analysis model for the pore unit (a)shaft before deformation[41]; (b)deformed shaft[41]; (c)analysis unit of shearing stress for the shaft[41]; (d)force analysis model for the pore unit |
由于扭转承载的变形状态,圆轴的圆柱面(图 9(c)中的面元ABCD)不存在切应力,而其横截面(图 9(b)中过线段A′B′和C′D′的截面)以及过其轴线的纵截面(图 9(b)中过线段A′C′和B′D′的截面)上均存在切应力(图 9(c)中的τ和τ′),并形成力平衡。
如果圆轴为网状多孔材料,将圆轴表层微元ABCD取为与多孔体中的某孔隙单元重合,则该孔隙单元即是受到名义切应力(源于上述名义扭矩)最大的单元。因此,要推演多孔体发生失效破坏时的载荷关系,即可用该孔隙单元来做受力分析(参见图 9(d))。
7.2.2.3 多孔构件承载准则参见式(7-13),多孔体在扭转载荷作用下,当σmax≥[σ]时,即:

|
(7-14) |
多孔体将会萌生整体性失效。
7.2.2.4 数理关系修正上述推导和分析为理想的简化状态,因此孔棱内部实际出现的最大拉应力应在理论导出的σmax的基础上加以修正。同前做指数项拓展,得出多孔体构件在扭转力作用下发生失效时TMAX与孔率的数理关系为:
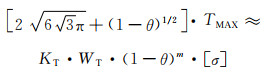
|
(7-15) |
圆轴的抗扭截面模量为:
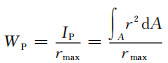
|
(7-16) |
式中:IP是圆轴构件横截面对截面中心的极惯性矩;rmax是横截面上距中心轴最远点到中心轴的距离;A是圆轴的横截面积。
对于孔隙分布均匀的多孔构件,在其有效横截面上实际可以积分的面积元应该是(dA)θ。因此,多孔构件的扭转截面模量为:
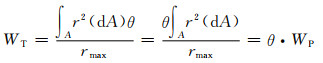
|
(7-17) |
将式(7-17)代入式(7-15),得:

|
(7-18) |
可将式(7-14)进一步表达为:
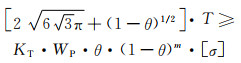
|
(7-19) |
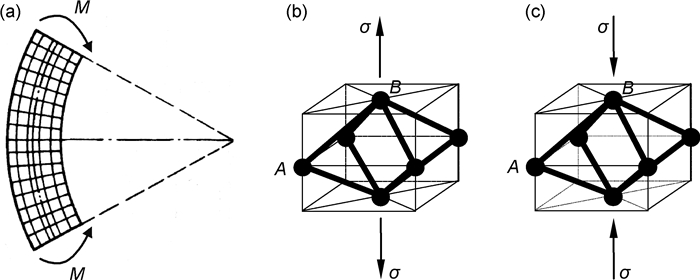
按照剪切载荷形式中的物理模型假设,建立三维同性均匀网状多孔材料的简化结构模型。多孔体构件承受弯矩M作用,由其在构件内部造成的孔棱最大正应力σmax达到对应材质许用应力[σ]时,就会萌发多孔体的整体性失效(参见图 10,内应力σ源于弯矩M作用)[42]。
|
图 10 弯曲载荷作用下多孔体中孔隙单元的受力分析模型 (a)弯矩M作用下的多孔元件[41]; (b)中性层左侧内部名义拉应力; (c)中性层右侧内部名义压应力 Fig. 10 Force analysis models of pore unit for the porous body under bending moment (a)porous component under bending moment M[41]; (b)internal nominal tensile stress on the left of the neutral layer; (c)internal nominal compressive stress on the right of the neutral layer |
如图 10(a)所示,当弯矩作用于多孔构件时,将会在平行于构件轴线的竖直方向于构件内部产生正应力。其中在构件中性面左边产生拉应力(图 10(b)),而在构件中性面右边产生压应力(图 10(c))。
八面体孔隙单元是排列规则的均匀结构,故在受到弯矩作用时,构件的最大内应力会发生在构件边缘位置。若多孔体的孔隙相对于多孔构件足够小,则除构件弯曲中性层的位置外(当然也可设定该中性层正好为两个孔隙单元的界面),八面体单元的孔棱此时在结构上和受力状态上都大致等价,因此任何一条孔棱都可表征单元中的其他孔棱。为便于分析计算,承受弯矩作用的构件以矩形截面杆件为例。如图 10(a)的弯矩作用,受力分析考虑有竖轴向拉伸力或压缩力的单元。即对八面体孔隙单元的孔棱AB只需考虑主单元,并将孔棱受力作悬壁梁近似处理。
取弯矩作用引起多孔构件最大名义内应力之处(即构件截面边缘或构件表层部分)的八面体单元为研究对象。图 10示出的多孔体构件在其左侧受到的拉伸正应力最大,对应表层最易发生失效破坏。从表层中的孔隙单元进行受力分析着手,可推演多孔体构件在弯矩作用下发生破坏时的相关载荷关系。此时除对八面体单元的载荷是由构件内部弯矩引起外,其受力分析状态完全类似于多孔材料单向拉伸。当然,直接切入的是构件中的弯矩,而获得构件破坏时的弯矩数理关系后,外加载荷即可通过弯矩关系而得以表达。
根据多孔材料单向拉伸的相关推演过程,按照获得其表达式中(1-θ)项指数拓展的方式,可得安全承载最大名义应力σMAX。
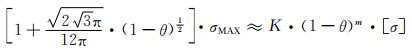
|
(7-20) |
弯矩M作用下构件中产生的最大内应力为:
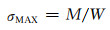
|
(7-21) |
将式(7-21)代入式(7-20)中,可得多孔构件在弯曲载荷作用下所能承受的最大名义弯矩:
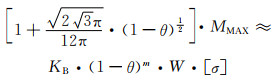
|
(7-22) |
根据构件对中性轴z的弯曲截面模量的定义,得多孔体弯曲截面模量为:
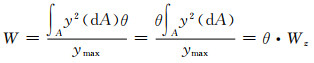
|
(7-23) |
式中:ymax是横截面上距中性轴z最远点到中性轴z的距离; Wz为对应致密构件的弯曲截面模量。
代入式(7-22),得:

|
(7-24) |
三维同性高孔率网状多孔材料可视为由大量孔棱按立方体对角线方式连接而形成的八面体孔隙单元集合[37]。参见图 1,单元八面体的正投影为侧置正方形,是单元八面体的综合体现,正方形的各边与八面体的中心对称轴呈45°角。不管多孔体所受载荷是循环拉压还是循环弯曲,都可归于单元八面体在各自轴向的往复拉压(其中循环弯曲作用时多孔构件中性层两侧的单元八面体拉压正好相对),即孔棱产生绕结点的来回偏转或具有这种趋势。因此,循环负荷性能最终可由孔棱所受的反复弯曲载荷来体现[43]。所以,在做多孔体的疲劳性能比较时,可归结为弯曲作用使孔棱产生的最大应力。即在同样的外加循环载荷作用下,同质孔棱产生的最大应力幅值越小,多孔体的疲劳性能越好。
8.2 数理关系推演 8.2.1 类应力疲劳根据循环应力的特性可将疲劳分为应力疲劳(高周疲劳)和应变疲劳(低周疲劳)[44]:前者的作用应力值小于屈服应力,发生破坏时所经历的应力循环周次(疲劳寿命)较高;后者的最大循环应力值大于屈服应力,发生破坏时具有较少的循环周次。因此,可将高周疲劳、高循环疲劳和应力疲劳视为同等概念[45]。本文的“类应力疲劳”,仅指多孔材料整体所受外加循环载荷为应力幅控制,不考虑“高周”或“高循环”。
8.2.1.1 数理关系由式(2-21)变形可得:
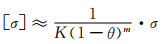
|
(8-1) |
该式表明,对多孔体所施外加载荷所致名义应力为σ时,孔棱产生的最大应力即为[σ],其发生于孔棱的表层。根据该式描述的关系可知,若外加于多孔体载荷所致名义应力幅值为σMAX,则孔棱表层产生的最大应力幅值σmax可表达为:
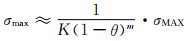
|
(8-2) |
在循环载荷作用下沿用这一关系,并令:
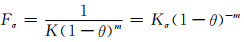
|
(8-3) |
式中:Fσ为取决于多孔体制备工艺、材质和孔率的因素;Kσ是与孔率无关而取决于多孔体制备工艺和材质的材料常数。结合式(8-2)和式(8-3)得:

|
(8-4) |
根据多孔材料抗拉强度的模型分析推演可知,式(8-1)源于弹性区推导(但其对多孔体名义失效应力的适用并不限于弹性区,因为可以将韧性材质多孔体的孔棱“一旦越过弹性极限而刚刚开始屈服即视为最终失效”,脆性材质多孔体不存在这个问题)。因此,式(8-2)~(8-4)适用范围是弹性应变区,即循环载荷对应的名义应力要小于多孔体静载失效名义应力。
8.2.1.2 对Fσ的分析对于同工艺制备的同质多孔材料,在同等循环载荷作用下,如果孔棱所受往复应力幅值σmax越大,则多孔体的疲劳损伤越严重。根据式(8-4),外加载荷对应名义应力幅值σMAX一定,则Fσ越大的材料其孔棱受力幅值σmax越大,多孔体越易产生疲劳。所以,Fσ可作为衡量多孔体类应力疲劳性能高低的指标。
当σmax达到弹性极限时,σMAX值若增加,则金属孔棱应变逐渐进入塑性区,式(8-4)不再适用。然而,对于同工艺同材质制备的多孔材料,在同一循环载荷条件下,若多孔体的Fσ越大,则应变超出弹性极限的距离也越远,故疲劳性能越差。因此,无论是在弹性区还是在塑性区内,Fσ都可作为衡量材料疲劳性能的指标。
总之,多孔体一旦发生受应力幅控制的疲劳现象,其疲劳性能就可用Fσ指标进行比较。式(8-3)表明,对于同工艺同材质制备的多孔体,孔率越高,则Fσ值就越大,即越易产生类应力疲劳。
8.2.2 类应变疲劳类应变疲劳仅指作用在多孔体上的外加循环载荷为应变幅控制,不考虑“低周”或“低循环”。数理推演:对于承受一定应变幅循环载荷的多孔体,其不同位置的孔棱弯曲偏转程度可以各不相同,但各条孔棱轴线的角度偏转幅总是保持不变。而对于具有一定轴线偏转幅的孔棱,如果孔棱越粗,弯曲处可以产生的最大伸缩量也会越大(该位置在孔棱的表层)。这时导致的应力幅值也会越高,故在同等循环载荷作用下多孔体越易疲劳。所以,当存在类应变疲劳问题时,从孔棱的粗细出发,可以找出衡量其疲劳性能的指标。
为便于计算,将单元八面体的孔棱视为圆柱形,则由式(1-5)给出的孔棱半径为:
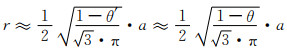
|
(8-5) |
根据本八面体模型理论和图 1,孔体形状可考虑为侧置正方形,如图 11所示(该图是图 1单元八面体孔隙的正向投影),其中b为孔体单元正投影的棱长,即相当于“正方形孔隙”的棱长,D则相当于“正方形孔道”的边长。

|
图 11 等效孔径分析图 Fig. 11 Diagram for the equivalent size of pore diameter |
b为:

|
(8-6) |
由式(8-5)和式(8-6),D即为:
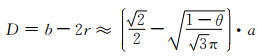
|
(8-7) |
设等效圆孔直径为d,则有:
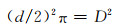
|
(8-8) |

|
(8-9) |
结合式(8-7)得:
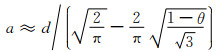
|
(8-10) |
将式(8-10)代入式(8-5)整理得:
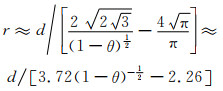
|
(8-11) |
对于不同工艺同种材质制备的多孔材料,孔棱形状偏离圆柱体的程度各不相同,故对应同样的轴线偏转幅会出现不同的最大形变幅,从而导致不同的最大应力幅。而对于不同材质制备的多孔体,即使工艺以及孔棱的形状和大小均一样,且轴线偏转幅度相同,产生的最大应力也会不同。因此,最大应力幅值应该是随Kεr(其中Kε是取决于多孔体制备工艺和材质的常数)而变。令:
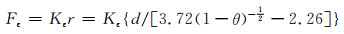
|
(8-12) |
式中Fε是取决于多孔体制备工艺和材质以及孔率和孔径的常数。Fε越大,在同一循环载荷作用下越易产生类应变疲劳。
9 多孔材料比表面积 9.1 比表面积分析模型将网状多孔材料的结构模型表征为由圆柱形孔棱规则地按立方体对角线方式连接而形成的大量八面体孔隙单元集合。多孔体内部孔隙的表面积主要贡献来自孔棱[46]。单元八面体中各条孔棱表面积的总和与包含该单元的立方体体积之比,即可表征多孔体的体积比表面积。
9.2 数理关系推演根据八面体孔隙单元模型(图 1)和结点剖面简图(图 2),可利用几何方法进行有关尺寸计算。单元八面体棱长L、孔棱半径r以及扣除结点损失的孔棱长度(有效计算长度)L′分别为:
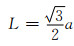
|
(9-1) |
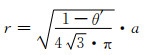
|
(9-2) |

|
(9-3) |
由此可得孔隙单元内全部孔棱的总表面积S为:
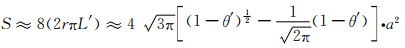
|
(9-4) |
式(9-4)未计入孔棱内部空隙的表面积(如中空表面积),是因为内部空隙很少(实心孔棱基本没有内部空隙),且占有闭孔,由于传质的关系,对多孔材料应用时的界面作用很小,可以忽略。如果这些空隙与外部连通参与作用,其表面贡献可纳入修正系数之中。
对于整个多孔体的比表面积,应该与其组成单元,即八面体孔隙单元的比表面积一致,故结合式(9-4)可得:
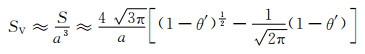
|
(9-5) |
基于式(8-9),对流体流经时表现出的有效孔径应为:
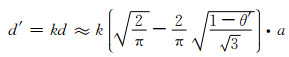
|
(9-6) |
由此得:
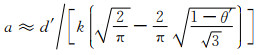
|
(9-7) |
式中k为流体效应校正系数,取决于多孔体细观结构方式,最终亦取决于材质和工艺条件。
将式(9-7)代入式(9-5)整理得:
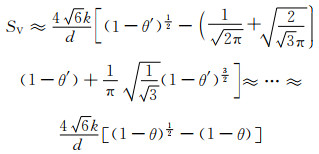
|
(9-8) |
由于实际的孔棱并非光滑的圆柱体,因材质和制备工艺的变化,可呈各种形状和赋予不同的表面状态,从而引起表面积不同程度的增加。此外,孔隙形状、孔径分布、孔棱具体结构方式和连接方式等因素,也都会影响到多孔体的对应比表面积。尽管情形复杂,但这些因素都直接与多孔材料的材质和制备工艺条件相关联。所以,式(9-8)可以用取决于材质和工艺的系数k′予以修正,简单的系数相乘法修正得:
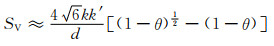
|
(9-9) |
令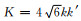

|
(9-10) |
对于三维网状结构的多孔材料,d值具有的是等效的意义,而且随不同的测量方法会有所不同,但它们之间只是倍乘的关系,可纳入常数项K中。因此,在量值测试过程中,应保持测量方法不变,而用显微法测d时还应保持同样的计数方式,这样才可使K值确定一致。
当材料为各向异性时,即使是同法测试,从不同的方向也会得出不同的d值。当然,这些不同方向的d值之间,也只是倍乘关系,而θ值则保持不变。所以,此时K值和d值均随取向而异,但对同一工艺方法制出的同种材料,它们为同倍增减,对SV不会产生影响。
另外,式(9-10)未考虑孔棱内部空洞缺陷对比表面积的贡献,这对估算可利用的比表面是合理的。因为孔棱内部空缺多为半通孔和闭孔隙,对扩散和界面作用几乎没有效能,而且对外部连通的大孔隙来说,它们所占体积份额一般相对很小。如果空缺是开口的,而且对介质作用达到相当的程度,那么可以视作孔棱表面的凹凸不平或坑洼来处理,其贡献可以体现在常数项K值中,无需另行计算。
9.3 理论公式修正代表性的网状多孔材料泡沫镍实验结果表明[24],在实验样品的孔率范围内,材料的平均孔径变化不大,但比表面积一直在随孔率提高而增大,特别是在孔率超过96%时,比表面呈急剧增大的趋势。经计算,式(9-10)与实验结果产生的偏差很大,考虑到研究多孔材料的传导性时也有电阻率随孔率提高而增大的规律(关系公式中有一项为“(1-θ)-1”)[25],于是,在式(9-10)的基础上进行倍乘一项“(1-θ)-1”的调试,得第一次修正式为:

|
(9-11) |
将式(9-11)应用于上述实验数据,结果有所好转,但计算偏差仍然很大。于是,进一步尝试将修正项的确定指数“-1”改换成除K之外的另一个非确定常数n,得:
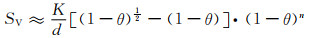
|
(9-12) |
修正思想是:多孔体比表面积与孔率和孔径的关系受制于2个因素,即关联材质和制备工艺的材料常数K以及关联孔隙几何因素的几何因子n,后者也是一个取决于多孔体制备工艺的材料常数。对于理论态,即有n=0。将式(9-12)再次实践于泡沫镍样品的实验结果[24],获得了很好的应用效果。于是,将式(9-12)最终确定为网状多孔材料比表面积的计算公式。
10 结束语由于多孔材料在工程应用中涉及物理、力学等多方面的性能,不同的性能要求对材料参数的选择不同,有时甚至是相互矛盾的。因此,需要对材料性能进行综合评估,选取合适的材料参数。本文即是在第一作者建立的多孔材料结构模型的基础上,根据其衍生拓展的结构-性能模型,推演各性能指标与结构参数(主要是孔率)的数理关系,以此为多孔材料制品的性能设计特别是综合性能设计提供参考。
文中理论公式只有在高孔率范围内才能适用,比如孔率为70%以上或更高的区间,但该区间足以覆盖此类产品的实际孔率范围。电沉积工艺制备的高孔率三维网状泡沫金属产品在欧、美、日及中国都有很高的产量,其使用性能优良,应用市场极大。电沉积基体通常为大块片材,但通过叠层烧结等处理方式可得到所需厚度更大的多孔制品。熔模铸造法、渗流铸造法等工艺制备的泡沫金属亦为网状结构,而金属熔体发泡类工艺制备的泡沫金属则多为胞状孔隙结构。对于力学性能,胞状泡沫金属所表现出来的性能孔率关系也有类似于三维网状体的一面。所以可以从三维网状结构入手,得出具有普适性的近似数理关系。
| [1] | LIU P S, LIANG K M. Functional materials of porous metals made by P/M, electroplating and some other techniques[J]. Journal of Materials Science, 2001, 36 (21): 5059–5072. DOI: 10.1023/A:1012483920628 |
| [2] | BANHART J. Manufacture, characterisation and application of cellular metals and metal foams[J]. Progress in Materials Science, 2001, 46 (6): 559–632. DOI: 10.1016/S0079-6425(00)00002-5 |
| [3] | TURNBULL M M, LANDEE C P. Porous materials with a difference[J]. Science, 2002, 298 (5599): 1723–1724. DOI: 10.1126/science.1078560 |
| [4] |
陈祥, 李言祥. 金属泡沫材料研究进展[J].
材料导报, 2003, 17 (5): 5–8.
CHEN X, LI Y X. Porous metals:research advances and applications[J]. Materials Review, 2003, 17 (5): 5–8. DOI: 10.3321/j.issn:1005-023X.2003.05.002 |
| [5] | LEFEBVRE L P, BANHART J, DUNAND D C. Porous metals and metallic foams:current status and recent developments[J]. Advanced Engineering Materials, 2008, 10 (9): 775–787. DOI: 10.1002/adem.200800241 |
| [6] |
刘培生, 陈祥, 李言祥.
泡沫金属[M]. 长沙: 中南大学出版社, 2012.
LIU P S, CHEN X, LI Y X. Metal foams[M]. Changsha: Central South University Press, 2012. |
| [7] |
刘培生.
多孔材料引论[M]. 2版. 北京: 清华大学出版社, 2013.
LIU P S. Introduction to porous materials[M]. 2nd ed. Beijing: Tsinghua University Press, 2013. |
| [8] | LIU P S, CHEN G F. Porous materials:processing and applica-tions[M]. Boston, USA: Elsevier Science, 2014. |
| [9] | ATWATER M A, GUEVARA L N, DARLING K A, et al. Solid state porous metal production:a review of the capabilities, characteristics, and challenges[J]. Advanced Engineering Materials, 2018, 20 (7): 1700766. DOI: 10.1002/adem.201700766 |
| [10] |
刘培生, 马晓明.
多孔材料检测方法[M]. 北京: 冶金工业出版社, 2006.
LIU P S, MA X M. Methods to measure porous materials[M]. Beijing: Metallurgical Industry Press, 2006. |
| [11] | LIU P S. Different theories application to foamed metals under biaxial equal-stress tension[J]. Materials Science and Engineering:A, 2004, 364 : 370–373. DOI: 10.1016/j.msea.2003.07.002 |
| [12] | VESENJAK M, VEYHL C, FIEDLER T. Analysis of anisotropy and strain rate sensitivity of open-cell metal foam[J]. Materials Science and Engineering:A, 2012, 541 : 105–109. DOI: 10.1016/j.msea.2012.02.010 |
| [13] | HUANG L, WANG H, YANG D H, et al. Effects of calcium on mechanical properties of cellular Al-Cu foams[J]. Materials Science and Engineering:A, 2014, 618 : 471–478. DOI: 10.1016/j.msea.2014.09.051 |
| [14] | PARVANIAN A M, SAADATFAR M, PANJEPOUR M, et al. The effects of manufacturing parameters on geometrical and mechanical properties of copper foams produced by space holder technique[J]. Materials & Design, 2014, 53 : 681–690. |
| [15] | XIAO L J, SONG W D, TANG H P, et al. High temperature compression properties of open-cell Ni-20Cr foams produced by impregnation[J]. Materials & Design, 2015, 85 : 47–53. |
| [16] | LIU P S, QING H B, HOU H L. Primary investigation on sound absorption performance of highly porous titanium foams[J]. Materials & Design, 2015, 85 : 275–281. |
| [17] | PALKA K, ADAMEK G, JAKUBOWICZ J. Compression beha-vior of Ti foams with spherical and polyhedral pores[J]. Advanced Engineering Materials, 2016, 18 (8): 1511–1518. DOI: 10.1002/adem.201600169 |
| [18] | LIU P S, QING H B, HOU H L, et al. EMI shielding and thermal conductivity of a high porosity reticular titanium foam[J]. Materials & Design, 2016, 92 : 823–828. |
| [19] | SUN J X, DUAN C Y, LIU P S. Sound absorption charac-terization of aluminum foam made by press infiltration casting[J]. Multidiscipline Modeling in Materials and Structures, 2016, 12 (4): 737–747. DOI: 10.1108/MMMS-03-2016-0010 |
| [20] | SIMONEAU C, TERRIAULT P, JETTE B, et al. Development of a porous metallic femoral stem:design, manufacturing, simulation and mechanical testing[J]. Materials & Design, 2017, 114 : 546–556. |
| [21] | ZHAI W, YU X, SONG X, et al. Microstructure-based experi-mental and numerical investigations on the sound absorption property of open-cell metallic foams manufactured by a template replication technique[J]. Materials & Design, 2018, 137 : 108–116. |
| [22] |
刘培生, 崔光, 程伟. 多孔材料性能模型研究1:数理关系[J].
材料工程, 2019, 47 (6): 42–46.
LIU P S, CUI G, CHEN W. Study on the property model for porous materials 1:mathematical relations[J]. Journal of Materials Engineering, 2019, 47 (6): 42–46. |
| [23] |
刘培生, 夏凤金, 罗军. 多孔材料模型分析[J].
材料工程, 2009 (7): 83–87.
LIU P S, XIA F J, LUO J. Analyses of the classical model for porous materials[J]. Journal of Materials Engineering, 2009 (7): 83–87. DOI: 10.3969/j.issn.1001-4381.2009.07.020 |
| [24] |
刘培生, 夏凤金, 程伟. 多孔材料性能模型研究2:实验验证[J].
材料工程, 2019, 47 (7): 35–49.
LIU P S, XIA F J, CHEN W. Study on the property model for porous materials 2:experimental verification[J]. Journal of Materials Engineering, 2019, 47 (7): 35–49. |
| [25] | LIU P S, LI T F, FU C. Relationship between electrical resis-tivity and porosity for porous materials[J]. Materials Science and Engineering:A, 1999, 268 : 208–215. DOI: 10.1016/S0921-5093(99)00073-8 |
| [26] | LIU P S.Chapter 3: porous materials.materials science research horizon[M].New York, USA: NOVA Science Publishers, 2007. |
| [27] | LIU P S. The tensile strength of porous metals with high poro-sity[J]. Journal of Advanced Materials, 2000, 32 (2): 9–16. |
| [28] | LIU P S. Tensile fracture behavior of foamed metallic materials properties[J]. Materials Science and Engineering:A, 2004, 384 (1/2): 352–354. |
| [29] | YANG Q C, ZHANG M J, LIU P S. Macroscopic fracture behavior of nickel foam under tension[J]. Multidiscipline Modeling in Materials and Structures, 2016, 12 (1): 110–118. DOI: 10.1108/MMMS-05-2015-0025 |
| [30] | GIBSON L J, ASHBY M F. Cellular solids:structure and prop-erty[M]. Cambridge, UK: Cambridge University Press, 1999. |
| [31] | LIU P S, FU C, LI T F. Relationship between elongation and porosity for high porosity metals[J]. Transactions of Nonferrous Metals Society of China, 1999, 9 (3): 546–552. |
| [32] |
王新桥, 陈静仪, 赵志敏, 等. 拉伸试验因素对拉伸细丝的力学性能影响[J].
功能材料, 1991, 22 (3): 160–167.
WANG X Q, CHEN J Y, ZHAO Z M, et al. Effect of tensile testing factors on mechanical properties of fine wire[J]. Journal of Functional Materials, 1991, 22 (3): 160–167. |
| [33] | LIU P S, CHEN G F, DUAN C Y. Investigation on Young's modulus and Poisson ratio of foamed metals[J]. Materials Science and Technology, 2011, 27 (10): 1498–1501. DOI: 10.1179/174328409X430528 |
| [34] | LIU P S. A new analytical model about the relationship between nominal failure stresses and porosity for foamed metals under biaxial tension[J]. Materials & Design, 2007, 28 (10): 2678–2683. |
| [35] | LIU P S, CHEN G F. Mechanical relation of foamed metals under uniaxial and biaxial loads of collective tension and compression[J]. Materials Science and Engineering:A, 2009, 507 (1/2): 190–193. |
| [36] | LIU P S, CHEN G F, CHEN Y M. Mechanical model of porous metal foams under multiaxial tensile loads[J]. Philosophical Magazine Letters, 2009, 89 (10): 655–663. DOI: 10.1080/09500830903246276 |
| [37] |
刘培生. 多孔材料在三向载荷作用下的力学模型[J].
材料科学与工艺, 2010, 18 (5): 609–613.
LIU P S. Mechanical model of porous materials under multiaxial loadings[J]. Materials Science & Technology, 2010, 18 (5): 609–613. |
| [38] |
刘培生. 泡沫材料在剪切载荷作用下的力学关系推演和分析[J].
稀有金属材料与工程, 2010, 39 (3): 457–459.
LIU P S. Deduction and analysis on mechanical relationship of porous open-cell metal foams under shearing loads[J]. Rare Metal Materials and Engineering, 2010, 39 (3): 457–459. |
| [39] | LIU P S. Mechanical relations for porous metal foams under several typical loads of shearing, torsion and bending[J]. Materials Science and Engineering:A, 2010, 527 (29/30): 7961–7966. |
| [40] |
刘培生, 罗军, 陈一鸣. 泡沫金属多孔体在扭矩作用下的分析表征[J].
清华大学学报(自然科学版), 2010, 50 (6): 932–935.
LIU P S, LUO J, CHEN Y M. Characterization of porous open-cell metal foams under torsion[J]. Journal of Tsinghua University (Science and Technology), 2010, 50 (6): 932–935. |
| [41] |
范钦珊, 蔡新.
工程力学[M]. 北京: 机械工业出版社, 2012.
FAN Q S, CAI X. Engineering mechanics[M]. Beijing: China Machine Press, 2012. |
| [42] |
刘培生, 陈一鸣, 丁晓纪. 泡沫金属在弯矩作用下的表征分析[J].
材料工程, 2009 (5): 65–67.
LIU P S, CHEN Y M, DING X J. Analysis of porous open-cell metal foams under bending moment[J]. Journal of Materials Engineering, 2009 (5): 65–67. DOI: 10.3969/j.issn.1001-4381.2009.05.016 |
| [43] |
刘培生, 马晓明. 高孔率泡沫金属材料疲劳表征模型及其实验研究[J].
材料工程, 2012 (5): 47–54.
LIU P S, MA X M. Fatigue model for foamed metals with high porosity and corresponding experimental study[J]. Journal of Materials Engineering, 2012 (5): 47–54. DOI: 10.3969/j.issn.1001-4381.2012.05.010 |
| [44] |
陈传尧.
疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002.
CHEN C Y. Fatigue and fracture[M]. Wuhan: Huazhong University of Science & Technology Press, 2002. |
| [45] |
徐灏.
疲劳强度[M]. 北京: 高等教育出版社, 1988: 9-146.
XU H. Fatigue strength[M]. Beijing: Advanced Education Press, 1988: 9-146. |
| [46] |
刘培生. 多孔金属比表面积的计算方法[J].
材料研究学报, 2009, 23 (4): 415–420.
LIU P S. Calculation method for the specific surface area of porous metals[J]. Chinese Journal of Materials Research, 2009, 23 (4): 415–420. DOI: 10.3321/j.issn:1005-3093.2009.04.015 |
 2019, Vol. 47
2019, Vol. 47