文章信息
- 苏继龙, 吴金东, 刘远力
- SU Ji-long, WU Jin-dong, LIU Yuan-li
- 蜂窝结构力学超材料弹性及抗冲击性能的研究进展
- Progress in elastic property and impact resistance of honeycomb structure mechanical metamaterial
- 材料工程, 2019, 47(8): 49-58
- Journal of Materials Engineering, 2019, 47(8): 49-58.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2018.001476
-
文章历史
- 收稿日期: 2018-12-27
- 修订日期: 2019-05-22
手性结构的概念在1989年被Wojchowski[1]提出,而具有手性蜂窝结构的超材料直到20世纪90年代才开始被研究。该类超材料因其独特的力、声、光以及电磁波动等性能,目前已受到世界各国学者的广泛关注[1-7]。内部具有手性蜂窝结构的超材料是一种具有内部拓扑结构可变、轻质、高比刚度,并具有负泊松比等优点的一种新型多孔拓扑材料[2]。与普通多孔拓扑材料相比,该类材料具有更好的抗冲击、抗凹、减振降噪和吸波的能力[3-7]。总之,因该类材料具有独特的力学和物理性能,并可对其内部微结构进行优化设计,已逐步引起国内外学者对其广泛的关注和研究[8-12]。
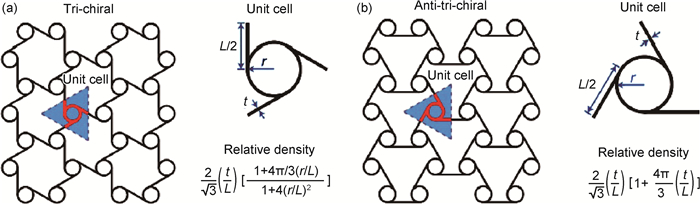
图 1为手性和反手性蜂窝结构、胞元以及相对密度的示意图。如图 1所示,手性蜂窝结构是由具有周期性分布的圆环状和弹性韧带切向连接形成的蜂窝型拓扑结构,由这种蜂窝结构拓展所实现的材料一般可称为力学超材料。随着对韧带布局和旋向的深入研究,很多新型的手性蜂窝结构被构建,并且针对其面内和面外弹性模量的研究已有很多结果[13-18],很多学者已经开始对手性系的蜂窝结构超材料的弹性性能进行归纳式的研究[19-21]。在抗冲击力学性能研究方面,通过对这种力学超材料进行有限元仿真和采用实验手段观察冲击载荷作用下不同手性蜂窝结构力学超材料的冲击形变特点,逐步分析和总结此类材料的抗冲击性能[22-28]。基于以上研究基础,本文重点梳理并总结了目前众多学者重点关注和研究的工程承载超材料,即具有手性蜂窝结构的力学超材料的变形模型构建、静态力学性能以及抗冲击性能的研究结果,并针对目前该类超材料在弹性和抗冲击性能研究方面所存在的一些问题提出相应的研究方向,以期为具有手性蜂窝结构的力学超材料的进一步研究和开发应用提供参考。
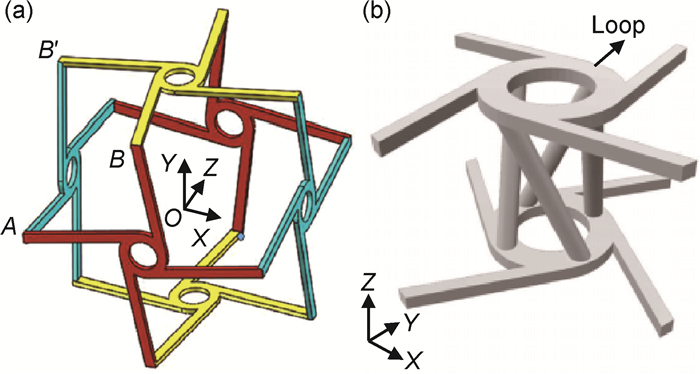
蜂窝结构力学超材料的原始制造材料(母体材料)可以是一般的高分子材料、金属及合金等,由圆形环体(节点环)及弹性韧带组成。其中韧带相切于圆环并将多环联结拓展,有序排列从而形成蜂窝拓扑结构。节点环旋转和韧带弯曲变形、节点环和韧带的尺寸、排列的方式是手性蜂窝结构力学超材料弹性性能和冲击性能的关键影响因素[6-12]。常见的韧带数量有三韧带、四韧带和六韧带等。韧带两端所连接的圆环处于韧带的两侧,称之为手性超结构;如果韧带两端所连接的圆环处于韧带的同一侧,则称之为反手性超结构(如图 1所示)。近年来,随着对手性蜂窝结构力学超材料的理论和实验研究的深入,一些新型的手性蜂窝结构也随之出现,如将内凹六边形和手性蜂窝结构结合,便可使其满足与血管壁内膜的变形特性匹配的微型血管支架,其外观尺寸可以达到毫米量级。另外,目前已有3D形式的手性蜂窝结构力学超材料出现,如图 2所示。
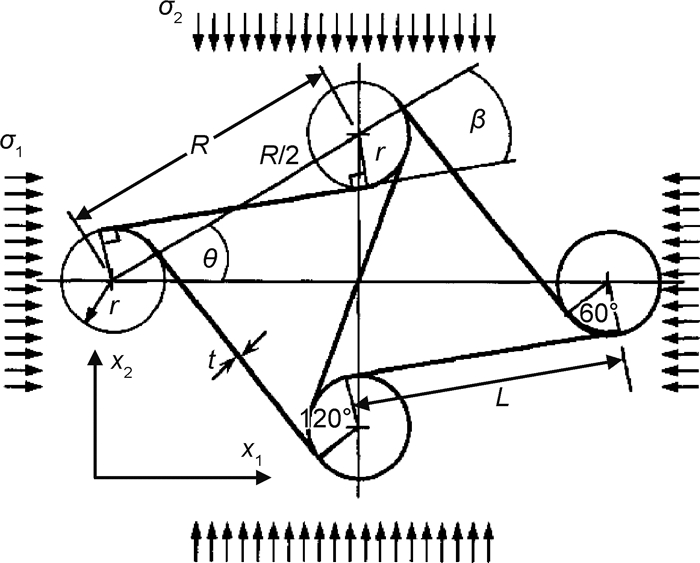
自1987年Lakes[8]首次通过对普通聚氨酯泡沫的处理获得具有特殊微观结构的负泊松比材料,并测得其泊松比值为-0.7后,新的更高的负泊松比材料,即具有“拉胀”特性的材料相继出现:Chan等[9]采用一种新的制备方法,其所制备的拉胀泡沫材料的回弹韧性和能量吸收性能均得到了明显的提高,而普通泡沫的杨氏模量增加到一定程度后,材料迅速发生弹性崩塌。随着对负泊松比材料的制备和负泊松比产生机理的进一步研究,一些新型负泊松比材料也相继出现。Gibson等[10]在普通蜂窝的基础上设计出了内凹六边形蜂窝,并且推导其杨氏模量和泊松比的解析式,得出其泊松比为-1。Lakes[11]从微观的单元结构上总结了产生负泊松比应该具备以下条件:旋转自由度、非放射性的动力学性能或者各向异性,并列举了普通蜂窝结构、内凹六边形蜂窝结构来论证自己的观点。值得注意的是,前期负泊松比材料的研究主要集中在高分子材料领域,因这类泡沫材料的强度不高,承受载荷的能力较差,工程应用受到一定的限制。因此,Lakes[11]首次提出了六韧带手性蜂窝结构的力学超材料(非中心对称结构),该类材料可以使用金属母体材料制作,且此类手性蜂窝结构可以满足以上“拉胀”产生的基本条件,所以此种手性蜂窝结构力学超材料可以产生负泊松比并且可以显著提高工程承载能力。Prall等[12]基于韧带变形模式对六韧带蜂窝结构力学超材料的负泊松比进行研究并对该种结构胞元产生负泊松比的力学机理首次进行了较为详细的描述(见图 3)。Prall等[12]基于韧带的欧拉梁理论和小变形的情况下,推导出其泊松比为-1。同时采用能量法推出该六韧带胞元的杨氏模量为[12]:
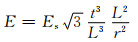
|
(1) |
式中:t为厚度;L为韧带长度;r为节点圆半径;Es为母体材料的杨氏模量。该结果与Gibson所得到的普通蜂窝材料的杨氏模量Es(t3/L3)的表达式及其影响因素的结论相似[14]。最后,Prall等[12]结合实验证明了其理论的准确性,为该类蜂窝结构力学超材料的进一步分析和计算提供了理论基础。但是该理论是基于弹性变形的前提,所推导的是手性蜂窝结构力学超材料面内的泊松比和弹性模量,对于面外的整体和压缩冲击下局部的弹塑性变形尚没有提及。Spadoni等[15]进行了六韧带手性蜂窝结构力学超材料的面外压缩实验,研究了在静载作用下六韧带蜂窝结构力学超材料的整体和局部的线性屈曲行为。同时,Spadoni等[15]采用经典的薄板壳屈曲理论,研究了材料整体发生压缩屈曲时的变形和临界载荷,得到面外平面压强作用下韧带薄板的临界载荷和节点圆所在的圆桶平面的临界载荷分别为:

|
(2) |
式中:K为影响系数(它取决于沿平行于载荷的边缘施加的边界条件);Es,νs 分别为材料本体的杨氏模量和泊松比;t为壁厚;L为韧带长度。该模型初步反映出力学超材料整体性能与内部微结构紧密相关。另外,Spadoni等[15]通过采用薄板和壳的线性屈曲经典分析理论和有限元模型研究手性六边形蜂窝结构力学超材料的面外强度,指出可以通过修改韧带尺寸和角度等参数来改善面外承载性能,为蜂窝型夹层结构的柔性设计提供了力学分析基础。2007年,Scarpa等[16]研究了六韧带手性蜂窝结构的弹性屈曲行为,证明了圆柱为整个蜂窝结构提供了主要的面外承载能力且最先发生屈曲的部分是韧带,圆柱形节点环抗屈曲的能力高于韧带的抗屈曲能力;其研究结果还表明六韧带的负泊松比效应可以有效地缓解鞍形面的产生。Lorato等[17]采用解析、有限元和实验相结合的方法,研究了六、四、三手性蜂窝结构的面外弹性性能(压缩模量和横向剪切模量),研究结果表明手性蜂窝结构力学材料的压缩模量等于单元的承载面积和总面积之间的比值,即承载单元的密度与总密度之间的比值。对应到具体的六韧带、四韧带手性蜂窝超材料中:
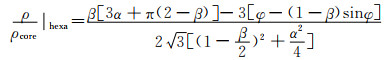
|
(3) |
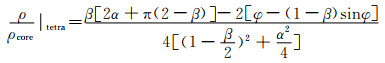
|
(4) |
式中:α=L/r, β=t/r, φ=cos-1(1-β)。对于横向的剪切模量,因为手性蜂窝结构力学超材料为非中心对称材料,所以其剪切模量大小的上下限分别为:
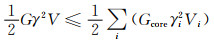
|
(5) |
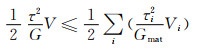
|
(6) |
式中:γ=u/b,τ=F/S,τ为切应力,u为单元长度,b为单元厚度;F为剪切力,S为受力面积,V为体积;G为母体材料的剪切模量。结果表明,对于不同韧带的手性蜂窝结构力学超材料而言,连接度较高(韧带分布较密)的蜂窝结构比连接度较低的蜂窝结构具有更好的横向剪切模量响应,但它们都与材料的内部结构有关。
同样,Alderson等[18]系统地研究了几类常见的三、四、六正/反手性蜂窝结构力学超材料的面内力学性能,分析了其变形机理以及弹性模量和泊松比的性质,提出了韧带的弯曲变形模式,发现手性系蜂窝结构的变形机理和负泊松比的性质存在明显的相似性;Miller等[19]对六韧带和四韧带手性蜂窝结构的屈曲行为进行参数优化分析,阐述了手性蜂窝结构的几何形状对屈曲行为有重要的影响,手性蜂窝结构比普通六边形蜂窝更能抵抗屈曲。Chen等[20]研究了各向异性的四韧带反向手性蜂窝结构面外和面内的力学性能,将泊松比、剪切模量、杨氏模量的理论结果、实验结果、有限元计算结构(如图 4所示)进行比较,系统地分析了该蜂窝结构力学超材料的力学性能。
Mousanezhad等[13]采用能量法系统地研究了手性蜂窝结构、反手性蜂窝结构、六边形和方形分层蜂窝的弹性性能,包括弹性模量、泊松比和剪切模量,并提出了内部韧带弯曲变形的力学机理。
目前,国内针对手性蜂窝结构力学超材料的弹性性能的研究主要有:2013年赵显伟[21]成功推导出四韧带同向手性蜂窝结构的面内杨氏模量、泊松比、面外杨氏模量以及剪切模量的上限,他采用均匀化方法对四韧带同向手性蜂窝结构的弹性模量和泊松比进行有限元计算和预测,并结合理论和实验对其进行综合的比较,研究了四韧带同向手性蜂窝结构力学性能与其几何参数间的变化关系,同时得到了面外杨氏模量和面内杨氏模量间的变化关系,并且对其面外剪切模量的变化趋势进行了分析。赵显伟还研究了四韧带手性蜂窝结构同时实现最小密度和面内最大弹性模量以及面外最大杨氏模量和面外最小杨氏模量的可能性,为今后手性蜂窝结构力学超材料的性能柔性化可变设计提供了理论依据。在弹性波传播和抑制方面,徐时吟等[24]针对中低频段,基于周期结构的Bloch定理以及有限元理论,对六韧带手性胞元的频散特性进行了研究,得到了胞元的能带结构,同时分析了胞元的几何参数与节点填充材料对手性结构能带的影响。这些研究揭示了手性蜂窝结构超材料在多领域的应用及其性能的柔性可调控性。
总之,具有负泊松比特性的蜂窝结构力学超材料有多种构建形式,主要体现在其母体材料有高分子聚合物、一般金属或合金以及其具有不同形式的内部微结构拓扑。现有文献结果表明,目前众多学者针对这类超材料的微观结构的构造方法与形变机理做了大量的工作,并已提出了几种解释负泊松比效应的机理。从这些研究结果中可以得到结论:具有负泊松比特性的力学超材料所具有的独特性能取决于其特殊的内部结构。但宏观性能与内部结构之间的定量关系还不是很清晰,现有的研究大多数还是在忽略一些因素的前提下采用有限元数值模拟和初步实验的方法。
3 蜂窝结构力学超材料抗冲击性能的研究现状 3.1 蜂窝结构力学超材料抗冲击性能的理论分析在工业领域特别是航空航天领域,对轻质、隔振、抗冲击等防护材料要求越来越高。随着手性蜂窝结构力学超材料日益被视为可替代传统冲击防护材料、能量吸收填充材料以及工程构件时,对其冲击变形特性和动态冲击强化等动力学性能的深入研究显得尤为重要。而从力学角度看,抗冲击性能的研究关键是确定外力和材料内部韧带及节点环上的作用力的大小。这方面的研究,针对一般传统蜂窝和泡沫材料已有很多重要的研究结果[25-37]。
牛斌等[25]针对传统周期性蜂窝材料提出了一种基于微极连续体等效分析理论的计算微单胞构件中应力分布的快速算法。不同于细观力学中采用体积平均的均匀化方法,牛斌等所提出的方法可以定量计算原结构微观层次应力、应变的准确信息,对局部微观结构的裂纹开裂、构件失稳等破坏行为的研究,特别是建立外载与内部受力之间的关系提供了解析分析的参考。但这种细观力学方法的计算比较繁琐,且内部微结构尺寸参数的影响等也不能很直观地体现,且主要针对的是一般传统蜂窝型材料。
对于冲击时的临界压力,Coté等[26]推导了四方形不锈钢金属蜂窝芯和直边为双倍厚度的商用六边形蜂窝芯材料的弹性屈曲临界应力公式,并分析了相对密度、试样高度与内部蜂窝孔洞尺寸比值以及边界约束等因素对压缩性能的影响,但这些研究主要依靠实验测试,没有详尽的解析推导且研究对象仍然是一般的蜂窝材料。张大军等[27]考虑了邻接孔壁的约束作用,提出了合理的非等壁厚蜂窝壁板的侧边条件,建立了求任意尺寸比的蜂窝材料面外受压时的初始弹性失稳载荷的力学模型,克服了失稳载荷经验公式求解精度的不足,然而该方法只适于求解弹性屈曲临界应力值,对整体材料抗冲击承压性能尚无具体研究结果。刘强等[28]基于一般的二维蜂窝结构的代表性单元,建立了金属蜂窝材料弹塑性屈曲的力学分析模型,进而推导出六边形蜂窝在面外载荷作用下的弹塑性临界应力:
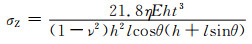
|
(7) |
式中:η=Et/E;Et为切线模量;E为杨氏模量;ν为泊松比;其余为六边形蜂窝的基本结构参数。该公式反映了蜂窝材料的几何特征及其母材的力学性能,并可通过单参数表征该类金属蜂窝材料的弹塑性屈曲特性。
而对于本文所述的手性蜂窝结构力学超材料,针对其抗冲击性能研究的解析方法,特别是外部载荷与内部微结构上受力关系的确定的相关文献较少。主要研究有:张政等[38]用能量法和泛函数极值分析的方法,分别探讨了六韧带手性蜂窝材料在受到面内冲击时缓冲第一阶段中韧带的冲击动荷系数及韧带失稳坍塌临界压力,得到了韧带的动荷系数表达式为:
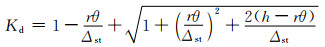
|
(8) |
式中:r为节点圆半径;θ为旋转角;Δst为位移常数;h为重物下落高度。失稳临界压力的解析表达式:
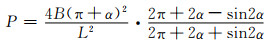
|
(9) |
式中:B=EI, EI为韧带梁抗弯刚度;L为韧带长度;α为初始相位角(即韧带与节点圆切线间的夹角)。结果表明:韧带节点环在冲击压缩变形过程中扭转角越大,韧带的动荷系数越小,而韧带的失稳临界压力随着节点环的扭转角的增大而增大。该研究结果初步探讨了内部微结构变形和失稳的判据,但尚未建立在冲击的第一阶段宏观外部力和内部力之间的传递规律。
3.2 整体动载冲击下的有限元仿真和实验研究由于解析方法的模型建立的复杂性和准确性限制,很多学者采用数值模拟方法进行手性蜂窝结构力学超材料冲击性能的研究。有限元仿真作为研究冲击性能的有效方法在很多冲击工程中得到广泛的应用,它在蜂窝型结构材料的研究上首先针对的对象就是一般普通蜂窝材料:Ruan等[39]利用Abaqus对六角形铝蜂窝进行有限元动态冲击模拟,得到了六角形铝蜂窝在不同冲击速率下的面内整体变形模式:在低冲击速率下肋架首先产生局部变形从而形成倾斜的X形条带(X模态),在高冲击速率下产生垂直于加载方向的垂直I形条带(I模态)。当速率适中时,出现的是过渡式V型模式。当冲击速率增加时,局部“变形带”出现在靠近加载侧面板边缘的位置,且减小细胞壁厚度与增加冲击速率具有相同的效果,都将导致局部变形条带更靠近加载边缘区。张新春等[40]研究了面内冲击载荷作用下不同形状单胞的动态变形机制及能量吸收特性。在相对密度及单胞边长尺寸一致的条件下,讨论了3种不同形状的单胞(三角形、正方形和六边形)冲击变形模态。在此基础上,分析了一定冲击速率下,几何拓扑结构对单胞能量吸收特性的影响,其研究主要针对一般蜂窝材料且没有开展内部传力机制的分析,但所得到的冲击特性与材料内部拓扑结构紧密相关的结论为手性蜂窝结构力学超材料冲击性能的研究提供了思路。
卢子兴等[41]率先对手性蜂窝材料的动载冲击响应进行了研究,其利用显式动力有限元软件研究了四韧带手性蜂窝在不同冲击速率下的变形模式和能量吸收等动力学响应特性,并同普通六边形蜂窝的冲击行为进行了对比。通过计算得到了这两种蜂窝的变形模式图、动力响应曲线和能量吸收曲线,得到的结论是手性蜂窝具有显著的吸收中、低速冲击能量的潜质,并揭示了节点环的转动动能在手性蜂窝结构能量吸收中的重要性,为该类抗冲击材料内部结构优化设计提供理论依据,但同样没有针对冲击速率和胞元微观结构受力之间的耦合关系进行深入研究。
张新春等[42]建立了六韧带手性蜂窝结构力学超材料的有限元模型,具体讨论了冲击速率和胞元微结构参数对手性蜂窝材料的面内宏/微观变形行为、密实应变、动态平台应力和比能量吸收能力的影响。研究结果表明,随着冲击速率的增加,六韧带手性蜂窝结构表现为3种宏观变形模态: “><”型模式、“过渡”模式和“I”型模式,研究结果进一步反映了韧带和节点环在冲击吸能上的作用。随后卢子兴等[43]采用有限元数值模拟方法,研究了四韧带反手性蜂窝结构力学超材料在不同冲击速率下的变形模式和能量吸收等动力学响应特性,并与内凹六边形蜂窝的冲击行为作比较。结果表明:尽管凹六边形蜂窝材料的能量吸收能力明显大于手性蜂窝结构的超材料,但是由于内凹六边形蜂窝材料的致密化应变较小,平台区长度较短从而限制了其实际应用,而基于韧带和节点环旋转机制的四边反手性蜂窝材料的能量吸收潜力更大。
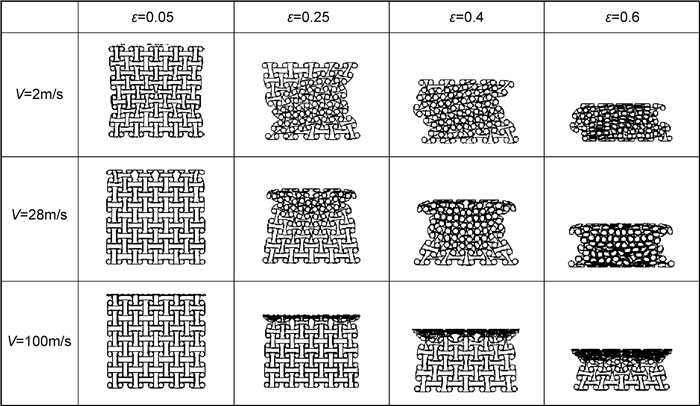
卢子兴等[44]对手性蜂窝结构力学超材料(手性和反手性蜂窝结构力学超材料)进行了面内冲击性能仿真实验,结果发现:各种不同类型手性系蜂窝结构力学超材料的变形模式较为一致。在低速冲击下,手性蜂窝的变形可分为两个阶段:第一个阶段为联接韧带的弯曲卷绕和节点圆环的转动,第二阶段为圆形环孔壁的坍塌。在高速冲击下,变形表现为圆形节点环和联接韧带的交替坍塌,胞元逐层压溃。而在中速冲击下,则表现为兼有低速和高速模式部分特征的过渡V模式(如图 5所示)。随着冲击速率的提高,局部变形区由固定端逐步发展到冲击端并且能量吸收能力也随之增强。同时,在中、低速冲击下,部分手性蜂窝结构力学超材料呈现出动态负泊松比效应。由此可见,不同蜂窝结构力学超材料在不同冲击速率下的能量吸收情况不同,其中四边反手性蜂窝结构力学超材料的能量吸收能力表现得最强,这也同样反映出内部微结构对材料整体抗冲击性能存在显著的影响。
蜂窝结构力学超材料作为一类负泊松比材料,其具备负泊松比“拉胀”材料的所有优势:(1)杨氏模量和剪切模量特性,即具有极高的压缩性却很难发生剪切;(2)整体变形行为,即在弯曲时不会产生马鞍形;(3)断裂韧度良好等[45]。因此很多学者将手性蜂窝结构力学超材料填充在具体的一些特殊工程结构或构件中,并以此来研究其整体的抗冲击和抗弯曲性能。章振华等[46]研究了圆孔结构、手性结构与反蜂窝结构3种覆盖层“抗冲瓦”模型,从抗冲瓦的相对密度、棱边长度、不同拓扑结构等微观结构参数的角度对该夹层瓦结构进行优化,并且还提出了新型双层抗冲瓦:圆孔结构和手性蜂窝超结构的结合体。研究结果表明,将手性蜂窝结构作为抗冲瓦的镂空填充结构,可以有效提高抗冲瓦片的抗冲击性能,尽管这只是实验层面上的结论,但也间接说明蜂窝结构力学超材料可以构成性能更优异的复合结构材料,并且其性能与层状结构的力学特征有关。江坤等[47]将六韧带手性蜂窝结构填充到舰船表面敷设的吸能覆盖层中,研究其整体在动态载荷下的压缩行为。研究结果表明,以超弹性材料为基底的六韧带手性蜂窝结构覆盖层具有更强的能量吸收能力和稳定性。
同样,肖锋等[48]将橡胶镂空成六韧带手性蜂窝材料填充到舰艇的覆盖层下,利用Abaqus有限元模快建立该材料的力学本构模型,然后分析手性蜂窝覆盖层的水下非接触性爆炸动响应特点,探索关键的设计参数包括厚度、镂空率和面板材料等对抗冲击性能的影响。研究结果表明,随着手性蜂窝结构力学超材料基本参数的改变和面板材料波阻抗的增加,覆盖层的抗冲击性能和缓冲性能得到显著提高。
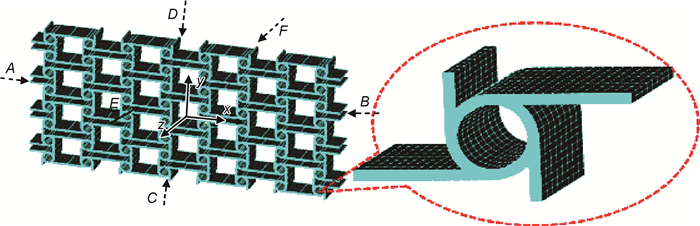
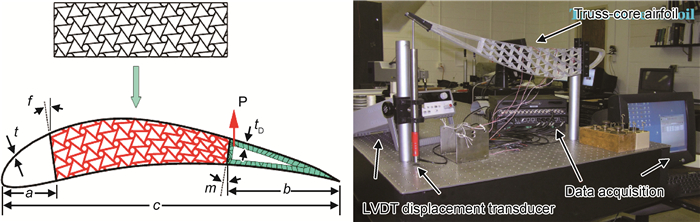
Spadoni等[49]将六韧带手性蜂窝结构力学超材料填充到大展弦机翼上(如图 6所示),并进行了内部结构的设计、仿真和实验,结果证明手性蜂窝结构填充材料可以承受大挠度的变形。赵显伟[21]将六韧带、四韧带同向、四韧带反向、三韧带同向、三韧带反向手性蜂窝结构力学超材料制作成飞机蒙皮的填充材料,搭建实验平台,模拟飞机飞行时所受的气动载荷来进行实验,并通过改变手性蜂窝结构力学超材料蒙皮的厚度,观察其承受弯曲的程度。实验结果表明手性蜂窝结构能够实现面内低模量和面外高承载要求,很适合作为变体飞行器的机翼蒙皮结构。任宪奔等[50]在手性蜂窝超结构超材料覆盖层的圆柱空腔中嵌入芯体,得到一种改进型手性蜂窝超结构,并进行分离式霍普金森压杆(SHPB)实验,通过SHPB实验及数值仿真研究其抗冲击性能,分析其能量吸收性能及变形特征。实验和仿真的结果都表明:在冲击作用下,改进型手性周期结构的芯体在自身惯性效应下在结构中作受迫振动并通过自身运动来吸收部分冲击能量,很明显地提高了力学超材料覆盖层的抗冲击性能。目前,除了作为承载结构材料,手性蜂窝结构超材料在隐身功能等领域也同样具有优异的功能[51-54]。本文所讨论的手性蜂窝结构力学超材料在以上这些工程结构等领域中的应用研究,也进一步说明手性蜂窝结构力学超材料在工程实践中具有强大和广泛的应用潜力。因此,对其性能与内部微结构关系的研究至关重要。
4 结束语蜂窝结构力学超材料由于其独特的多参数微结构和优异的力学性能,且具有轻质、负泊松比、高剪切模量及良好的抗缺口、抗断裂以及高回弹韧性,受到了国内外研究人员的高度关注。由于其内部拓扑结构尺寸可以实现毫米-厘米量级的拓展,手性蜂窝结构力学超材料不仅在生活和医用用品如血管支架、瓶塞、坐垫[51]上得到应用,同时在重要的工业领域,如航空、国防、电子产业也具有巨大的潜在应用价值[52-54]。近年来,关于手性蜂窝结构力学超材料的研究取得了许多积极成果,但大部分停留在实验制备与模拟仿真分析阶段。目前在该领域存在的一些问题以及发展趋势概述如下:
(1) 建立手性蜂窝结构力学超材料宏观性能与其内部微结构之间的关联模型。目前针对手性蜂窝结构力学超材料的研究主要侧重于构建新型的手性蜂窝结构、预测其准静态力学性能及解释负泊松比形成机理上。但是针对这些弹性性能参数如杨氏模量与内部胞元拓扑形态及尺寸之间的一般耦合控制关系、手性蜂窝结构力学超材料的面外韧带屈曲和内部损伤的机理都需要通过构建宏、细观关系的细观力学理论做进一步探索。
(2) 进一步探索手性蜂窝结构力学超材料抗冲击吸能性能的内部微结构变形机制。针对该类材料抗冲击性能的研究目前主要集中在对整体面内冲击变形和吸能模式进行有限元数值仿真。尽管手性蜂窝结构力学超材料在动载冲击下负泊松比的产生机理和静态时的一致性已经被证明,但是对冲击时内部韧带的受力和变形与实际的外部冲击大小之间的定量关系研究缺乏合理的力学模型。同时,关键的初始冲击吸能阶段的发生机理尚需要研究者进行深入、系统的探讨。
(3) 建立3D手性蜂窝结构力学超材料微细加工制造力学模型。随着对2D手性蜂窝结构力学超材料研究的深入,已有学者结合3D打印技术加工出了微小结构(如医用血管支架等)的3D手性蜂窝支架结构。因此,从3D设计制造及应用的角度开展该类超材料的微细加工制造的力学理论的探索具有重要的意义。
| [1] | WOJCHOWSKI K W. Two-dimensional isotropic system with a negative Poisson's ratio[J]. Physics Letters A, 1989, 137 (Suppl 1/2): 60–64. |
| [2] | GIBSON L J, ASHBY M F.Cellular solids: structure and proper-ties.2nd ed.[M].Cambridge: Cambridge University Press, 1997. |
| [3] | LIU H H. A review on auxetic structures and polymeric materials[J]. Scientific Research and Essays, 2010, 5 (10): 1052–1063. |
| [4] | SPADONI A, RUZZENE M, GONELLA S, et al. Phononic properties of hexagonal chiral lattices[J]. Wave Motion, 2009, 46 (7): 435–450. DOI: 10.1016/j.wavemoti.2009.04.002 |
| [5] | TEE K F, SPADONI A, SCARPA F, et al. Wave propagation in auxetic tetrachiral honeycombs[J]. Journal of Vibration and Acoustics, 2010, 132 (3): 1–8. |
| [6] |
于相龙, 周济. 智能超材料研究与进展[J].
材料工程, 2016, 44 (7): 119–128.
YU X L, ZHOU J. Research advance in smart metamaterials[J]. Journal of Materials Engineering, 2016, 44 (7): 119–128. |
| [7] |
礼嵩明, 蒋诗才, 望咏林, 等. "超材料"结构吸波复合材料技术研究[J].
材料工程, 2017, 45 (11): 10–14.
LI S M, JIANG S C, WANG Y L, et al. study on "metamaterial" structural absorbing composite technology[J]. Journal of Materials Engineering, 2017, 45 (11): 10–14. DOI: 10.11868/j.issn.1001-4381.2016.000152 |
| [8] | LAKES R S. Foam structures with a negative Poisson's ratio[J]. Science, 1987, 235 : 1038–1040. DOI: 10.1126/science.235.4792.1038 |
| [9] | CHAN N, EVANS K E. Fabrication methods for auxetic foams[J]. Journal of Materials Science, 1997, 32 (22): 5945–5953. DOI: 10.1023/A:1018606926094 |
| [10] | GIBSON L J, ASHBY M. Cellular solids[M]. Oxford: Pergamon Press, 1988. |
| [11] | LAKES R S. Deformation mechanisms of negative Poisson's ratio materials:structural aspects[J]. Journal of Materials Science, 1991, 26 (9): 2287–2292. DOI: 10.1007/BF01130170 |
| [12] | PRALL D, LAKES R S. Properties of a chiral honeycomb with a Poisson's ratio-1[J]. International Journal of Mechanical and Science, 1996, 39 : 305–314. |
| [13] | MOUSANEZHAD D, HAGHPANAH B, GHOSH R, et al. Elastic properties of chiral, antichiral, and hierarchical honeycombs:a simple energy-based approach[J]. Theoretical and Applied Mechanics Letters, 2016, 6 (2): 81–96. |
| [14] | GIBSON L J, ASHBY M F. The mechanics of three-dimen-sional cellular materials[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1982, 382 (1782): 43–59. DOI: 10.1098/rspa.1982.0088 |
| [15] | SPADONI A, RUZZENE M, SCARPA F. Global and local linear buckling behavior of a chiral cellular structure[J]. Physica Status Solidi (b), 2005, 242 (3): 695–709. |
| [16] | SCARPA F, BLAIN S, LEW T, et al. Elastic buckling of hexagonal chiral cell honeycombs[J]. Composites Part A (Applied Science and Manufacturing), 2007, 38 (2): 280–289. DOI: 10.1016/j.compositesa.2006.04.007 |
| [17] | LORATO A, INNOCENTI P, SCARPA F, et al. The transver-se elastic properties of chiral honeycombs[J]. Composites Science and Technology, 2010, 70 (7): 1057–1063. DOI: 10.1016/j.compscitech.2009.07.008 |
| [18] | ALDERSON A, ALDERSON K L, ATTATD D, et al. Elastic constants of 3-, 4- and 6-connected chiral anti-chiral honey-combs subject to uniaxial in-plane loading[J]. Composites Science and Technology, 2010, 70 (7): 1042–1048. DOI: 10.1016/j.compscitech.2009.07.009 |
| [19] | MILLER W, SMITH C W, SCARPA, F, et al. Flatwise buck-ling optimization of hexachiral and tetrachiral honey-combs[J]. Composites Science and Technology, 2010, 70 (7): 1049–1056. DOI: 10.1016/j.compscitech.2009.10.022 |
| [20] | CHEN Y J, SCARPA F, LIU Y J, et al. Elasticity of anti-tetrachiral anisotropic lattices[J]. International Journal of Solids and Structures, 2013, 50 (6): 996–1004. DOI: 10.1016/j.ijsolstr.2012.12.004 |
| [21] |
赵显伟.可变形蜂窝结构的力学性能分析[D].哈尔滨: 哈尔滨工业大学, 2013. ZHAO X W.The analysis of mechanical properties of morphing honeycomb structures[D]. Harbin: Harbin Institute of Technology, 2013. |
| [22] | FU M H, LIU F M, HU L L. A novel category of 3D chiral material with negative Poisson's ratio[J]. Composites Science and Technology, 2018, 160 : 111–118. DOI: 10.1016/j.compscitech.2018.03.017 |
| [23] | FU M H, ZHENG B B, LI W H. A novel chiral three-dimen-sional material with negative Poisson's ratio and the equivalent elastic parameters[J]. Composite Structures, 2017, 176 : 442–448. DOI: 10.1016/j.compstruct.2017.05.027 |
| [24] |
徐时吟, 黄修长, 华宏星. 六韧带手性结构的能带特性[J].
上海交通大学学报, 2013, 47 (2): 167–172.
XU S Y, HUANG X C, HUA H X. Study on the band structure of hexagonal chiral structures[J]. Journal of Shanghai Jiaotong University, 2013, 47 (2): 167–172. |
| [25] |
牛斌, 阎军, 程耿东. 周期性蜂窝材料微极等效模型及其微观应力的一种快速算法[J].
固体力学学报, 2008, 29 (2): 109–112.
NIU B, YAN J, CHENG G D. Micropolar continuum modeling of 2D periodic cellular materials and a fast mapping algorithm for the micro-stress[J]. Chinese Journal of Solid Mechanics, 2008, 29 (2): 109–112. |
| [26] | COTÉ F, DESHPANDE V S, FLECK N A, et al. The out-of-plane compressive behavior of metallic honeycombs[J]. Materials Science & Engineering A(Structural Materials:Properties, Microstructure and Processing), 2004, 380 (1/2): 272–280. |
| [27] |
张大军, 余同希. 蜂窝材料面外受压时初始弹性失稳载荷的计算[J].
上海交通大学学报, 1990, 24 (5): 47–55.
ZHANG D J, YU T X. The calculation of the initial bucking load of honeycombs under out-of-plane compression[J]. Journal of Shanghai Jiaotong University, 1990, 24 (5): 47–55. |
| [28] |
刘强, 黄争鸣. 金属蜂窝材料的弹塑性屈曲临界应力值[J].
力学季刊, 2008, 29 (4): 515–520.
LIU Q, HUANG Z M. Elasto-plastic buckling critical stress of metal honeycomb[J]. Chinese Quarterly of Mechanics, 2008, 29 (4): 515–520. |
| [29] | MOUSANEZHAD D, GHOSH R, AJDARI A, et al. Impact resistance and energy absorption of regular and functionally graded hexagonal honeycombs with cell wall material strain hardening[J]. International Journal of Mechanical Sciences, 2014, 89 : 413–422. DOI: 10.1016/j.ijmecsci.2014.10.012 |
| [30] | ZHOU H, XU P, XIE S, et al. Mechanical performance and energy absorption properties of structures combining two Nomex honeycombs[J]. Composite Structures, 2018, 185 : 524–536. DOI: 10.1016/j.compstruct.2017.11.059 |
| [31] | LI S Q, LI X, WANG Z H, et al. Sandwich panels with layered graded aluminum honeycomb cores under blast loading[J]. Composite Structures, 2017, 173 : 242–254. DOI: 10.1016/j.compstruct.2017.04.037 |
| [32] | LIU Q, FU J, WANG J S, et al. Axial and lateral crushing responses of aluminum honeycombs filled with EPP foam[J]. Composites Part B, 2017, 130 : 236–247. DOI: 10.1016/j.compositesb.2017.07.041 |
| [33] | CHEN H, ALESSANDRO F, LIU S, et al. Effect of honey-comb core under hypervelocity impact:numerical simulation and engineering model[J]. Procedia Engineering, 2017, 204 : 83–91. DOI: 10.1016/j.proeng.2017.09.759 |
| [34] | QIAO J X, FEI Q G, ZHANG P W. In-plane crushing of a hierarchical honeycomb[J]. International Journal of Solids and Structures, 2016, 85-86 : 57–66. DOI: 10.1016/j.ijsolstr.2016.02.003 |
| [35] | CHEN Y Y, LI T T, JIA Z, et al. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations[J]. Materials & Design, 2018, 137 : 226–234. |
| [36] |
鲁超, 李永新, 董二宝, 等. 零泊松比蜂窝芯等效弹性模量研究[J].
材料工程, 2013 (12): 80–84.
LU C, LI Y X, DONG E B, et al. Equivalent elastic modulus of zero Poisson's ratio honeycomb core[J]. Journal of Materials Engineering, 2013 (12): 80–84. |
| [37] |
李响, 周幼辉, 童冠. 类蜂窝结构的面内冲击特性研究[J].
西安交通大学学报, 2017, 51 (3): 80–86.
LI X, ZHOU Y H, TONG G. In-plane dynamic impact charact-eristic of the quasi-honeycomb structure[J]. Journal of Xi'an Jiaotong University, 2017, 51 (3): 80–86. |
| [38] |
张政, 苏继龙. 六韧带手性蜂窝材料韧带的冲击动荷系数及稳定性分析[J].
复合材料学报, 2019, 36 (5): 1313–1318.
ZHANG Z, SU J L. Dynamic coefficient and stability analysis of ligament of impacted hexachiral honeycomb[J]. Acta Materiae Compositae Sinica, 2019, 36 (5): 1313–1318. |
| [39] | RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs-a finite element study[J]. International Journal of Impact Engineering, 2003, 28 (2): 161–182. DOI: 10.1016/S0734-743X(02)00056-8 |
| [40] |
张新春, 刘颖. 面内冲击载荷作用下蜂窝材料单胞动态变形机制的研究[J].
科学技术与工程, 2007, 7 (12): 2799–2802.
ZHANG X C, LIU Y. Dynamic deformation mechanism of cells with different shapes under in-plane impact loading[J]. Science Technology and Engineering, 2007, 7 (12): 2799–2802. DOI: 10.3969/j.issn.1671-1815.2007.12.013 |
| [41] |
卢子兴, 李康. 四边手性蜂窝动态压溃行为的数值模拟[J].
爆炸与冲击, 2014, 34 (2): 181–187.
LU Z X, LI K. Numerical simulation on dynamic crushing behaviors of tetrachiral honeycombs[J]. Explosion and Shock Waves, 2014, 34 (2): 181–187. |
| [42] |
张新春, 祝晓燕, 李娜. 六韧带手性蜂窝结构的动力学响应特性研究[J].
振动与冲击, 2016, 35 (8): 1–7.
ZHANG X C, ZHU X Y, LI N. A study of dynamic response characteristics of hexagonal chiral honeycombs[J]. Journal of Vibration and Shock, 2016, 35 (8): 1–7. |
| [43] |
卢子兴, 李康. 负泊松比蜂窝动态压溃行为的有限元模拟[J].
机械强度, 2016, 38 (6): 1237–1242.
LU Z X, LI K. Dynamic crushing of honeycombs with a negative Poisson's ratio[J]. Journal of Mechanical Strength, 2016, 38 (6): 1237–1242. |
| [44] |
卢子兴, 李康. 手性和反手性蜂窝材料的面内冲击性能研究[J].
振动与冲击, 2017, 36 (21): 16–22.
LU Z X, LI K. In-plane dynamic crushing of chiral and anti-chiral honeycombs[J]. Journal of Vibration and Shock, 2017, 36 (21): 16–22. |
| [45] |
李竞, 王宇, 吴红枚, 等. 具有负泊松比材料的研究进展[J].
江西化工, 2016 (1): 69–73.
LI J, WANG N, WU H M, et al. Advances in research on with negative Poisson's ratio materials[J]. Journal of Jiangxi Chemical, 2016 (1): 69–73. DOI: 10.3969/j.issn.1008-3103.2016.01.021 |
| [46] |
章振华, 谌勇, 华宏星, 等. 抗冲瓦的结构研究及创新设计[J].
噪声与振动控制, 2012, 32 (6): 100–104.
ZHANG Z H, CHEN Y, HUA H X, et al. Research of anti-shock layer and innovation design[J]. Noise and Vibration Control, 2012, 32 (6): 100–104. |
| [47] |
江坤, 陶猛. 六韧带手性蜂窝结构覆盖层的动态压缩行为研究[J].
舰船科学技术, 2017, 39 (19): 55–60.
JIANG K, TAO M. A study of the dynamic compression behavior of hexagonal honeycomb layer[J]. Ship Science and Technology, 2017, 39 (19): 55–60. |
| [48] |
肖锋, 华宏星, 谌勇, 等. 设计参数对手性蜂窝橡胶覆盖层水下爆炸抗冲击性能的影响[J].
振动与冲击, 2014, 33 (1): 56–62.
XIAO F, HUA H X, CHEN Y, et al. Influence of design parameters on underwater explosion shock resistance of chiral honeycomb rubber cladding[J]. Journal of Vibration and Shock, 2014, 33 (1): 56–62. DOI: 10.3969/j.issn.1000-3835.2014.01.010 |
| [49] | SPADONI A, RUZZENE M. Numerical and experimental anal-ysis of static compliance of chiral truss-core airfoils[J]. Journal of Mechanics of Materials and Structures, 2007, 2 (5): 965–981. DOI: 10.2140/jomms.2007.2.965 |
| [50] |
任宪奔, 赵鹏铎, 李晓彬, 等. 改进型手性周期结构覆盖层的抗冲击性能研究[J].
振动与冲击, 2017, 36 (15): 142–145.
REN X B, ZHAO P D, LI X B, et al. Shock-resistant performance of cover layer on a new chiral periodic structure[J]. Journal of Vibration and Shock, 2017, 36 (15): 142–145. |
| [51] |
崔世堂, 王波, 张科. 负泊松比蜂窝面内动态压缩行为与吸能特性研究[J].
应用力学学报, 2017, 34 (5): 919–924.
CUI S T, WANG B, ZHANG K. Mechanical behavior and energy absorption of honeycomb with negative Poisson's ratio under in-plane dynamic compression[J]. Chinese Journal of Applied Mechanics, 2017, 34 (5): 919–924. |
| [52] |
邢丽英, 刘俊能. 蜂窝夹层结构吸波材料研究[J].
材料工程, 1992 (6): 15–18.
XING L Y, LIU J N. The study of honeycomb sandwich microwave absorbing materials[J]. Journal of Materials Engineering, 1992 (6): 15–18. |
| [53] | HOU Y, TAI Y H, LIRA C, et al. The bending and failure of sandwich structures with auxetic gradient cellular cores[J]. Applied Science and Manufacturing, 2013, 49 (3): 119–131. |
| [54] |
陈以金.变体飞行器柔性蒙皮及支撑结构性能研究[D].哈尔滨: 哈尔滨工业大学, 2014. CHEN Y J. Study on flexible skin and supporting substructure of morphing aircraft[D]. Harbin: Harbin Institute of Tech-nology, 2014. |
 2019, Vol. 47
2019, Vol. 47