文章信息
- 周强, 程军, 于振涛, 崔文芳
- ZHOU Qiang, CHENG Jun, YU Zhen-tao, CUI Wen-fang
- 一种新型近β型Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金热变形行为
- Hot deformation behavior of new type of near β type Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe alloy
- 材料工程, 2019, 47(6): 121-128
- Journal of Materials Engineering, 2019, 47(6): 121-128.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2018.000273
-
文章历史
- 收稿日期: 2018-03-18
- 修订日期: 2018-07-24
2. 西北有色金属研究院 陕西省医用金属材料重点实验室, 西安 710016;
3. 西北工业大学 凝固技术国家重点实验室, 西安 710072
2. Shaanxi Key Laboratory of Biomedical Metal Materials, Northwest Institute for Non-ferrous Metal Research, Xi'an 710016, China;
3. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi'an 710072, China
钛合金因其低密度、高比强度、耐腐蚀等优点而广泛应用于航空航天、汽车及生物医学等领域,长期以来一直是材料科学领域的研究热点。钛合金一般分为α, α+β, β三大类[1],其中的β钛合金因其具有高比强度、综合性能优异而成为研究和工程应用最为广泛的一类钛合金。Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe(质量分数/%)是西北有色金属研究院研发的一种新型高强-高韧近β钛合金,经一定热处理后室温抗拉强度可达到1200MPa,伸长率可达10%的良好强韧性匹配度。但该合金在热加工过程中对热变形参数(温度和变形速率等)十分敏感,如若控制不当,会出现开裂和不均匀变形等现象,导致物料报废。因此,通过系统研究该合金的热变形行为,建立材料的本构方程和热加工图,从而获得最优化的热变形工艺参数显得尤为必要。国内外有关学者针对β钛合金的热变形行为开展了相关工作,西北工业大学樊江昆等[2]研究发现Ti-7333合金在α+β两相区热变形的主要软化机制为动态回复和α相球化,β相区热变形的主要软化机制为动态再结晶。北京航空材料研究院王哲等[3]研究表明,变形温度对新型超高强韧TB17钛合金的动态再结晶行为有重要影响,在相变点温度以下变形仅发生初生α相再结晶,而相变点温度以上变形则发生β相动态再结晶。Bobbili等[4]研究表明,Ti-10V-2Fe-3Al合金在热压缩及模拟计算过程中,如果变形区域中各元素的总应变大于所需临界应变,组织会发生动态再结晶(DRX),相反则不发生。而目前针对Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金的热变形行为方面的研究比较少。
本工作以Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金的热压缩数据为基础,探讨在不同热变形条件下,热变形参数对合金流变应力的影响,建立了变形温度、应变速率与流变应力之间的流变应力本构模型,并绘制出热加工图,通过比较功率耗散值的大小,结合热加工图内不同典型区域的显微组织演变规律特征,分析了合金的热变形机制,为确定合适的热加工工艺参数和指导合金实际生产提供了理论基础和数据支持。
1 实验材料与方法本实验采用的合金为经2次真空自耗熔炼炉制备得到的ϕ160mm钛合金铸锭,其化学成分如表 1所示。通过淬火金相法测得合金相变点约为765℃。铸锭经开坯锻造和多次反复镦拔,最终获得ϕ50mm的圆棒。
| Mo | V | Cr | Al | Sn | Fe | O | Ti |
| 5.4 | 5.9 | 7.1 | 3.8 | 1.8 | 1.1 | 0.12 | Bal |
经单相区850℃/30min,AC固溶处理后,利用线切割沿轴向切取ϕ8mm×12mm的压缩试样。然后在Gleeble-3800热模拟试验机上进行等温热压缩实验,试样两端放置钽片和石墨乳作为润滑以减小摩擦。实验温度分别为:655,705,755,805,855℃;应变速率分别为0.001,0.01,0.1,1,10s-1;最大应变量为0.8。以10℃/s的速率将试样加热到指定的温度,保温5min后进行压缩,通过热电偶及时获得变形温度、变形速率、真应力、真应变等数据,绘制真应力-应变曲线以及热加工图。
压缩完成后立即水冷以保留高温变形后的组织,利用线切割沿试样轴向对半剖开,经磨、抛光和腐蚀制备金相试样,腐蚀液配比为HF:HNO3:H2O=1:2:7(体积分数),通过Axio Vert.A1型光学金相显微镜观察材料热变形后的显微组织形貌特征。
2 实验结果 2.1 真应力-真应变曲线图 1为合金在不同热变形条件下的真应力-真应变曲线。从图 1可知,在变形初始阶段,应力几乎呈直线上升,当应力到达峰值后,应力将随应变的持续增加而逐步减小直至趋于稳态流变特征,此后流变应力将不再随应变的变化而变化,处于稳态流变阶段。在材料变形的初始阶段,应变速率从零逐步增大到设定值,组织中的位错密度不断增大,产生形变硬化,应力呈直线上升态势,当应力到达峰值后,由于组织中可能伴随有动态回复与动态再结晶,并且此时的软化作用大于硬化作用,使得应力逐渐降低。当应变值继续增大,因软化作用与应变硬化作用达到动态平衡,应力值到达平稳阶段[5]。从图 1可知,合金的变形抗力比较大, 最高接近500MPa。在应变速率为10s-1的变形条件下,流变应力到达峰值后持续下降并出现波动,呈现出流动软化的特征。从图 1(a),(b)可知,随温度的升高流动软化特征逐渐向高应变速率方向转移。一般认为,材料在低温、高应变速率条件下变形时,由于局部温升,易导致绝热剪切及局部塑性流动等流变失稳现象的出现[6-7]。图 2为峰值应力与温度、应变速率的关系曲线图。由图 2可见,在一定的变形温度条件下,随应变速率的升高,流变应力增加;相反,在一定的应变速率条件下,随变形温度的升高,流变应力值降低。
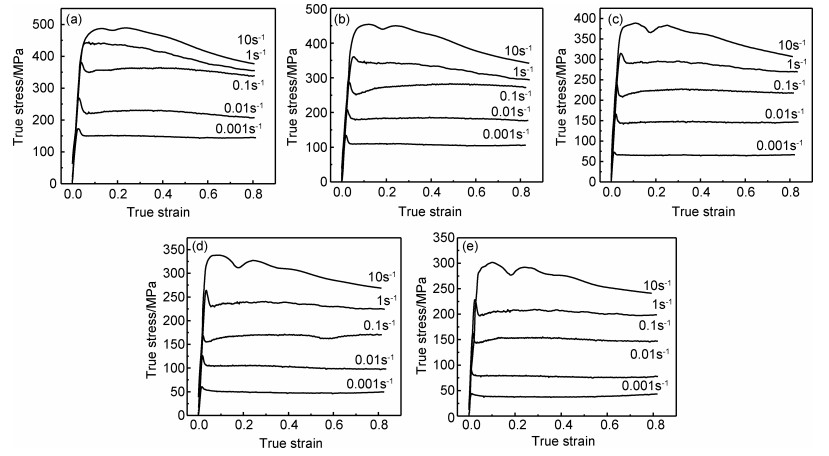
|
图 1 合金在不同变形温度和应变速率下的真应力-真应变曲线 (a)655℃;(b)705℃;(c)755℃;(d)805℃;(e)855℃ Fig. 1 Curves of true stress-strain of alloy at various deformation temperatures and strain rates (a)655℃; (b)705℃; (c)755℃; (d)805℃; (e)855℃ |
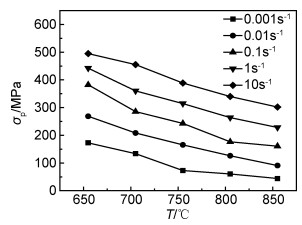
|
图 2 峰值应力与变形温度和应变速率的关系曲线 Fig. 2 Relation curves of peak stress and deformation temperatures and strain rates |
钛及钛合金本构方程的建立,通常在Arrhenius型本构方程基础上[8-9],同时采用双曲正弦模型式(1)来表达其流变应力与变形温度、变形速率之间的关系,以此可以定量描述材料的热压缩变形行为。
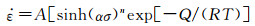
|
(1) |
式中:σ为流变应力;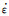
材料的指数关系模型以及幂指数关系模型如下:
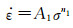
|
(2) |
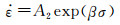
|
(3) |
式中:A1和A2是常数;n1和β是材料常数。对式(2)和(3)两边取对数得:

|
(4) |
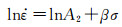
|
(5) |
取相应
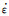
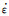
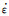
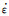
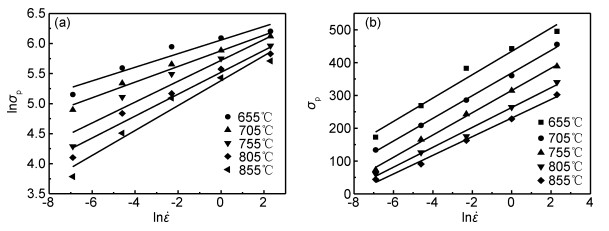
|
图 3 lnσp-ln   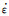 |
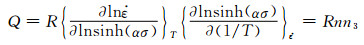
|
(6) |
式中:n3为温度敏感因子。同样采用线性回归处理,绘制出不同温度下相应的lnsinh(ασ)-ln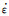
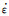
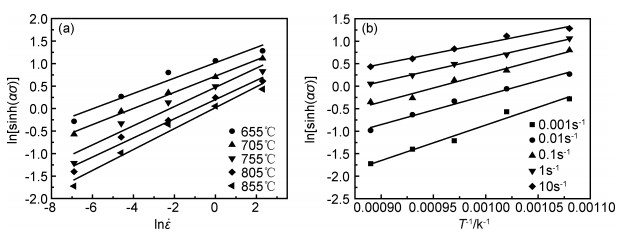
|
图 4 lnsinh(ασ)-ln  |
将各参数代入到式(6)中,计算得出变形激活能Q=255kJ/mol,而β钛合金中Ti的自扩散激活能153kJ/mol,说明在热变形过程中的变形机制不只是由动态再结晶控制,还伴随着动态回复的发生[10]。
热变形过程中,由于T和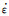
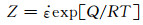
|
(7) |
代入到式(1)中可得:
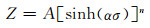
|
(8) |
对式(8)两边取对数得:
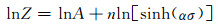
|
(9) |
在应力应变曲线中取一定的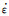
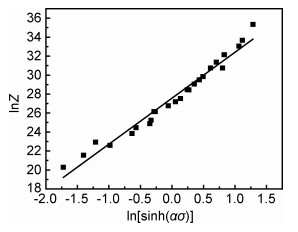
|
图 5 ln[sinh(ασ)]-lnZ的关系曲线 Fig. 5 Relation curve of ln[sinh(ασ)]-lnZ |
根据图 5求得lnA=27.56968,n=4.84353。将所得参数代入到式(1)中可得合金的热变形本构关系方程为:
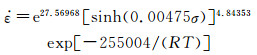
|
(10) |
DMM模型[10]是由Prasad在系统工程概念的基础上,基于大应变塑性变形的连续力学,物理系统模拟和不可逆热动力学等基本原理建立起来的。该模型的基本原理为变形体在单位时间塑性变形所消耗的总能量P分为两部分:以热能形式耗散的能量G和组织变化中所消耗的能量J。
Prasad等[11]将热模拟压缩数据利用3次样条函数拟合出lnσ与ln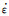
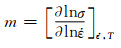
|
(11) |
功率耗散效率η的计算公式:
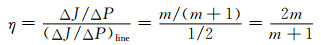
|
(12) |
可知参数η是一个关于温度、应变和应变速率的三元变量,在一定的应变量下,可将计算得出的η与温度及应变速率绘制出三维关系图,即功率耗散图。
在动态材料模型中,根据Ziegler[12]提出的加工失稳判据,Prasad[13]给出了材料流变失稳区的计算公式:
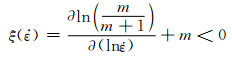
|
(13) |
式(13)的物理意义为当系统中熵的产生速率比外界施加的速率小,则系统将会出现局部的塑性流变,从而导致流动失稳现象。在一定应变量下,可得失稳系数ξ与温度、应变速率的等高线图,标记ξ(
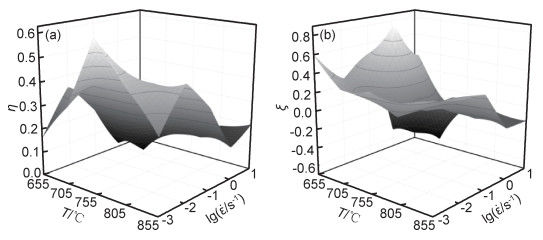
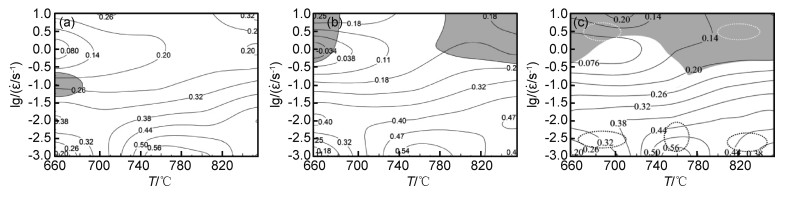
根据图 1中应力应变曲线,分别采集ε=0.2, 0.6, 0.8时不同应变速率和变形温度所对应的流变应力值,利用公式(11),(12),(13)计算出功率耗散率η以及失稳系数ξ,其中当应变为0.8,两者与应变速率和温度的三维关系如图 6所示。将三维的功率耗散图与失稳图转化为二维等高线图并叠加即可得合金热加工图,如图 7所示。图 7分别为真应变ε=0.2, 0.6, 0.8的热加工图。图中等高线的数值表示功率耗散值,一般功率耗散值较高的区域为适宜加工区域(加工安全区)。对比图 7(a)~(c)可以发现,随着应变的增大,功率耗散随温度和应变速率的变化大致相同,耗散峰值位置也基本相同,仅耗散值略有变化。并且功率耗散率η的最大值主要集中在相变点附近(750~770℃),低应变速率(0.001~0.003s-1)区域,最大值约为0.56。η最小值集中在大于1s-1高应变速率区域内。图中的阴影部分为加工失稳的区域,可以看出,各应变量下均出现了流变失稳区域,并随应变的增大,失稳区域逐渐向高应变速率方向移动。通过加工图提供的数据信息,可了解加工安全区和塑性失稳区等不同加工区域,以达到改善和优化合金的热加工工艺,指导实践并最终获得综合性能优良的产品。
|
图 6 功率耗散效率η(a)、失稳系数ξ(b)与应变速率和温度的三维关系图 Fig. 6 There-dimensional diagrams of efficiency of power dissipation (a)and buckling coefficient(b)with strain rate and temperature |
|
图 7 合金在不同应变量下的加工图 (a)ε=0.2;(b)ε=0.6;(c)ε=0.8 Fig. 7 Processing maps of alloy at different strains (a)ε=0.2;(b)ε=0.6;(c)ε=0.8 |
应变ε=0.8时,材料在高变形速率的变形下,其功率耗散系数较低,且多处在失稳区域,故该合金不适宜在高应变速率(如自由锻)条件下变形。功率耗散率η的最大值集中在相变点左右(750~770℃)、低应变变速率(0.001~0.003s-1)区域,η最小值集中在大于1s-1高应变速率区域内。在低应变速率,温度β转变点以下变形区域内,功率耗散值较低,且随着温度的升高功率耗散值逐渐增大,直到出现相变点附近的峰区。低温下的变形区域通常认为材料的软化机制为动态回复、α相的球化所致[14]。β转变点附近的中温峰区(750~770℃),最大功率耗散值在755℃,0.001s-1时大约为56%,该区域的软化机制可能由动态再结晶为主。相变点以上800~855℃温度范围内,功率耗散值逐渐减小,高温条件下材料的塑性流变能力提高,原始晶粒与再结晶晶粒逐渐长大。
2.3.2 安全区域分析Prasad[12]研究认为形核率以及晶界迁移率这两个过程共同控制动态再结晶的过程。当金属层错能低时,其形核率低,因此再结晶过程主要受形核率控制,功率耗散率也低。而钛合金的层错能高,形核率较高,故晶界迁移率控制了再结晶过程,导致耗散效率较高。
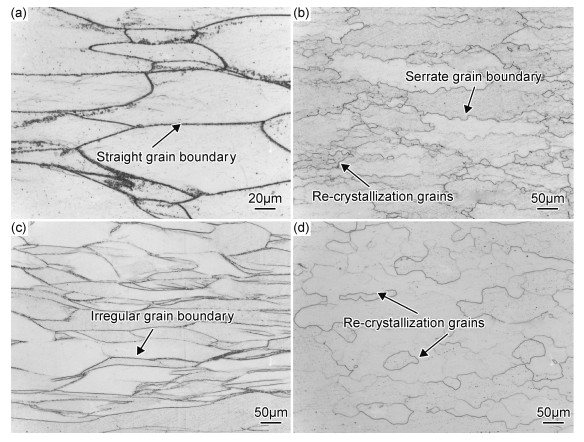
图 8为合金分别在655℃,0.001s-1和755℃,0.001s-1和755℃,1s-1以及855℃,0.001s-1变形条件下的显微组织图。由图 8(a)所示,合金在相变点以下的低温、低应变速率变形区域内,组织没有发生明显的动态再结晶。粗大的原始等轴β晶粒沿着垂直压缩轴向的方向变形拉长,并且晶内和晶界处析出许多细小的α相。合金在α+β两相区热变形时常常会析出α相,通常在此变形区域内在应力的作用下,α相的球化可能是材料的重要变形机制。由图 8(a)可知,合金在两相区热变形后,材料的显微组织由细小的球状或短棒状α相颗粒和β基体组成。说明在热变形条件下,α相发生了一定程度的球化,此过程是获得细小等轴α相的重要途径。1999年Seshacharyulu等研究发现[15]α相的球化过程可分为4个过程:板条相的剪切;位错的产生;位错界面的形成;界面分离。该区域主要的软化机制是动态回复和α相的球化。
|
图 8 不同变形条件下的显微组织 (a)655℃,0.001s-1;(b)755℃,0.001s-1;(c)755℃,1s-1;(d)855℃,0.001s-1 Fig. 8 Microstructures of deformed alloy at different temperatures and strain rates (a)655℃, 0.001s-1; (b)755℃, 0.001s-1; (c)755℃, 1s-1; (d)855℃, 0.001s-1 |
在相变点附近760℃,0.001s-1变形条件下的组织由图 8(b)所示,原始晶粒的晶内及晶界处均出现了动态再结晶晶粒,合金发生了明显的动态再结晶,并且α相已大量消失。热变形过程中,由于晶界处位错大量的塞积,造成应力集中,晶界迁移受到阻碍,使得原始变形晶粒的晶界变为锯齿状的不规则形状。此区域内动态再结晶是主要的软化机制。相同温度下,当变形速率增大到1s-1时,由图 8(c)所示,晶粒被明显拉长,没有明显的动态再结晶晶粒出现,晶界呈现不规则形状,是典型动态回复的特点。通常,合金在大应变速率条件下变形时,由于没有足够的时间使位错迁移以及异号位错的相互抵消等作用,小角晶界向大角晶界转化慢,使再结晶晶粒的形核率低,因此动态回复是合金的主要软化机制。当变形温度在相变点以上820~850℃的高温区域时,由图 8(d)所示,合金组织由粗大的变形β晶粒和部分再结晶晶粒组成,且在β晶粒中出现大量亚晶界。
2.3.3 失稳分析热加工图中,合金在高应变速率区域(>1s-1)变形时多处于流变失稳状态。材料热变形的失稳机制主要为局部的塑性流动,形成绝热剪切带以及楔形开裂等[16]。图 9为合金分别在655℃,10s-1和855℃,10s-1变形条件下的显微组织图。由图 9(a)所示,合金在655℃,10s-1变形时组织出现明显的绝热剪切带。热变形过程中,绝热剪切带在低温高应变速率变形条件下容易出现,在加工图上表现为功率耗散值低是由于大部分能量以热量的形式消耗在变形带上。并且,在压缩过程中切应力在与压缩轴线呈45°的方向上可达到最大值,宏观上产生45°剪切变形[17]。当变形温度与变形速率为855℃,1s-1时,图 9(b)所示,变形组织出现了局部塑形流动现象,变形的均匀性与组织的均匀性较差,此区域内不适宜加工。

|
图 9 不同变形条件下的显微组织 (a)655℃,10s-1;(b)855℃,10s-1 Fig. 9 Microstructures of deformed alloy at different temperatures and strain rates (a)655℃, 10s-1; (b)855℃, 10s-1 |
通常变形温度和变形速率对合金组织发生动态再结晶有重要影响,动态再结晶过程一般通过位错的聚集使得位相差逐渐增加,从而小角晶界逐渐向大角晶界转化进而产生新晶粒的连续过程[18]。变形过程中,晶界由于局部的迁移而呈现锯齿状,且在低变形速率条件下,小角晶界有足够的时间向大角晶界转化,动态再结晶容易发生。而变形温度对晶界的迁移也存在影响,当温度高时,原子扩散速率快,晶界迁移率快,动态再结晶也容易发生。所以合金在高温、低应变速率条件下,组织容易发生动态再结晶。相反,在低温、高应变速率条件下组织则主要以动态回复为主。因此Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金适宜加工区域为变形温度在相变点温度附近、低应变速率(750~770℃,0.001~0.003s-1),此条件下加工可获得细小的动态再结晶组织,最终获得较好的综合力学性能。
3 结论(1) Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金的流变应力随变形温度的升高而降低,随应变速率的增加而升高。
(2) Ti-5.5Mo-6V-7Cr-4Al-2Sn-1Fe合金的平均热变形激活能Q=255kJ/mol,大于β相的自扩散激活能为153kJ/mol,说明在变形过程中材料不仅发生了动态回复,还伴随有动态再结晶现象的发生。计算得出合金的流变应力模型为:
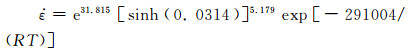
|
(3) 当应变速率大于1s-1的热变形条件下,功率耗散值低,材料多处于失稳状态,易发生绝热剪切与局部塑性流动等现象。在低应变速率条件下,变形温度在低于相变点温度时,材料的变形机制主要以动态回复为主;当变形温度在相变点以上时,材料的显微组织变化主要为动态再结晶,且随温度升高,组织逐渐粗大。
(4) 在变形温度为750~770℃,应变速率为0.001~0.003s-1的热变形条件下,材料功率耗散值达到最大值,且组织发生动态再结晶,该区域为合金适宜的加工区域。
| [1] |
李青云.
稀有金属材料加工手册[M]. 北京: 冶金工业出版社, 1984: 3-4.
LI Q Y. Rare metal processing manual[M]. Beijing: Metallurgical Industry Press, 1984: 3-4. |
| [2] | FAN J K, KOU H C, LAI M J, et al. Characterization of hot deformation behavior of a new near beta titanium alloy:Ti-7333[J]. Materials & Design, 2013, 49 : 945–952. |
| [3] |
王哲, 王新南, 商国强, 等. 新型超高强韧钛合金热变形行为研究[J].
稀有金属材料与工程, 2018, 47 (3): 810–815.
WANG Z, WANG X N, SHANG G Q, et al. Study on hot deformation behavior of new high strength and toughness titanium alloy[J]. Rare Metal Materials and Engineering, 2018, 47 (3): 810–815. |
| [4] | BOBBILI R, RAMUDU B V, MADHU V. A physically-based constitutive model for hot deformation of Ti-10-2-3 alloy[J]. Journal of Alloys & Compounds, 2016, 696 : 295–303. |
| [5] | WANG R, XI Z, ZHAO Y, et al. Hot Deformation microstructure and mechanism of Ti53311S titanium alloy[J]. Rare Metal Materials & Engineering, 2008, 37 (8): 1356–1359. |
| [6] | PRASAD Y V R K, SESHACHARYULU T. Processing maps for hot working of titanium alloys[J]. Materials Science & Engineering:A, 1998, 243 (1/2): 82–88. |
| [7] | TAMIRISAKANDALA S, BHAT R B, VEDAM B V. Recent advances in the deformation processing of titanium alloys[J]. Journal of Materials Engineering & Performance, 2003, 12 (6): 661–673. |
| [8] | SELLARS C M, TEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14 (9): 1136–1138. DOI: 10.1016/0001-6160(66)90207-0 |
| [9] | JONAS J J, SOMANI M C, TEGART W J. Strength and structure under hot-working conditions[J]. Metallurgica Reviews, 1969, 14 (1): 1–24. |
| [10] | PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of dynamic material behavior in hot deformation:forging of Ti-6242[J]. Metallurgical and Materials Transactions A, 1984, 15 (10): 1883–1892. DOI: 10.1007/BF02664902 |
| [11] | PRASAD Y V R K. Processing maps:a status report[J]. Journal of Materials Engineering & Performance, 2003, 12 (6): 638–645. |
| [12] | ZIEGLER H. Progress in solid mechanics[M]. New York: Wiley Press, 1963. |
| [13] | BHAT B V R, MAHAJAN Y R, ROSHAN H M, PRASAD Y. Processing map for hot working of powder[J]. Metallurgical Transactions A, 1992, 23 (8): 2223–2230. DOI: 10.1007/BF02646015 |
| [14] |
刘延辉, 姚泽坤, 宁永权, 等. 生物医用TC20钛合金高温变形行为及其本构关系[J].
材料工程, 2014 (7): 16–21.
LIU Y H, YAO Z K, NING Y Q, et al. Hot deformation behavior and constitutive relationship of biomedical TC20 alloy[J]. Journal of Materials Engineering, 2014 (7): 16–21. |
| [15] | SESHACHARYULU T, MEDEIROS S C, MORGAN J T, et al. Hot deformation mechanisms in ELI Grade Ti-6Al-4V[J]. Scripta Materialia, 1999, 41 (3): 283–288. DOI: 10.1016/S1359-6462(99)00163-3 |
| [16] | ZHU Y, ZENG W, FENG F, et al. Characterization of hot deformation behavior of as-cast TC21 titanium alloy using processing map[J]. Materials Science and Engineering:A, 2011, 528 (3): 1757–1763. DOI: 10.1016/j.msea.2010.11.015 |
| [17] |
黄烁, 王磊, 张北江, 等. GH4706合金的热变形行为与显微组织演化[J].
材料工程, 2015, 43 (2): 41–46.
HUANG S, WANG L, ZHANG B J, et al. Hot deformation behavior and microstructure evolution of GH4706 alloy[J]. Journal of Materials Engineering, 2015, 43 (2): 41–46. |
| [18] |
赵映辉, 葛鹏, 赵永庆, 等. Ti-1300合金的热变形行为研究[J].
稀有金属材料与程, 2009, 38 (1): 46–49.
ZHAO Y H, GE P, ZHAO Y Q, et al. Hot deformation behavior of Ti-1300 alloy[J]. Rare Metal Materials and Engineering, 2009, 38 (1): 46–49. |
 2019, Vol. 47
2019, Vol. 47


