文章信息
- 王波, 吴亚波, 黄喜鹏, 潘文革, 成来飞
- WANG Bo, WU Ya-bo, HUANG Xi-peng, PAN Wen-ge, CHENG Lai-fei
- 2D-C/SiC复合材料面内剪切性能统计及强度B基准值
- In-plane shear performance statistics of 2D-C/SiC composites and its B-basis value of strength
- 材料工程, 2019, 47(1): 131-138
- Journal of Materials Engineering, 2019, 47(1): 131-138.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2018.000260
-
文章历史
- 收稿日期: 2018-03-18
- 修订日期: 2018-08-29
2. 西北工业大学 力学与土木建筑学院, 西安 710072;
3. 西北工业大学 材料学院, 西安 710072
2. School of Mechanics, Civil and Architecture, Northwestern Polytechnical University, Xi'an 710072, China;
3. School of Materials Science and Engineering, Northwestern Polytechnical University, Xi'an 710072, China
碳纤维增韧碳化硅陶瓷基(C/SiC)复合材料由于其表现出的优越性能,如低密度、高耐热性以及伪韧性断裂行为,在航天航空、核工业等领域被视为最具潜力的候选材料[1-2]。然而,材料不可避免地存在原生裂纹或孔洞等缺陷,缺陷随机分布和生长导致材料性能表现出统计分布的特性,材料性能平均值已不能作为评价材料性能优劣的指标[3],应用统计学理论确定材料性能分布规律,并在此基础上寻找材料许用值尤为重要。
目前,关于陶瓷基复合材料性能分散性的统计研究并不多见,集中于拉伸和弯曲性能[4-8]。在国外,复合材料性能的分散性和可靠性问题也吸引着一些科学家的目光。Pitt等[9]考虑多种因素对复合材料强度的概率分布进行了系统研究;Calard等[10-11]发展了概率统计方法研究了二维编织SiC/SiC材料的失效强度;Genet等[12]基于多尺度计算方法建立了准脆性材料的强度分布模型。Richter等[13]研究了陶瓷基微复合材料的拉伸强度分布规律。关于陶瓷基复合材料B基准值鲜见文献报道,研究主要针对树脂基复合材料展开,涉及B基准值计算方法、计算程序设计以及比较不同算法之间的差异[14-17]。2D-C/SiC复合材料作为一种各向异性材料,剪切特性是其不可或缺的一个方面,且许多研究直接假设材料性能服从Weibull分布进行验证,忽略了其他分布的可行性。在检验材料性能分布时,会涉及经验失效概率,采用不同的经验失效概率对材料性能分布规律的检验结果有何影响也未作分析,并且没有在确定材料强度分布规律的基础之上更进一步——确定材料B基准值;此外,之前的研究对陶瓷基复合材料材料模量的分散性缺乏关注。因此,针对陶瓷基复合材料面内剪切性能统计及强度B基准值的问题还有待研究。
本工作采用2D-C/SiC复合材料约西佩斯库(Iosipescu)纯剪切试件,对其进行面内剪切实验,通过实验获得面内剪切模量和强度两项性能数据。分别用两种不同的经验失效概率,使用线性回归估计参数与Kolmogorov假设检验相结合的方法对2D-C/SiC复合材料面内剪切模量和强度性能进行统计研究,确定面内剪切强度和模量的分布规律和理论分布模型;也分析了用不同经验失效概率对材料性能统计过程以及结果的影响;通过观察试件最窄净截面微CT扫描照片和断口电镜扫描照片,解释了材料面内剪切强度分散性微观机制。最后计算出面内剪切强度的B基准值。
1 实验材料与方法2D-C/SiC复合材料采用化学气相渗透(CVI)工艺制备而成。试件密度约为2.0g/cm3,纤维体积分数约为40%,孔隙率约为19.5%。试件尺寸及应变片粘贴方式如图 1所示。面内剪切实验依照ASTM C1292-00实验标准,在DNS-100试验机进行。实验过程中试件表面粘贴BE120-2HA应变片,配合DH3820静态应变测试系统同步实时采集剪切应变。实验前采用Y.Cheetah X射线CT对试件最窄净截面进行扫描,获得扫描图像;实验后采用Quanta650f扫描电镜对断口进行显微观察。
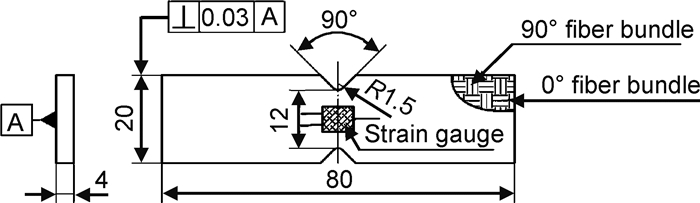
|
图 1 面内剪切试件 Fig. 1 In-plane shear specimen |
图 2是破坏后试件照片,破坏发生在最窄净截面处,形成平断口,0°纤维束全部发生剪切破坏,表面抗氧化基体部分脱落。图 3为实验得到的典型应力应变曲线,曲线整体呈非线性,这是由于材料本身的非均匀性,相邻纤维束之间以及横纵纤维搭接处均有较大空穴,随着应力的增加,空穴尖端应力集中导致的裂纹扩展以及空穴闭合,导致材料性能的宏观非线性关系[18]。

|
图 2 试件断口 Fig. 2 Fractured surfaces on specimens |
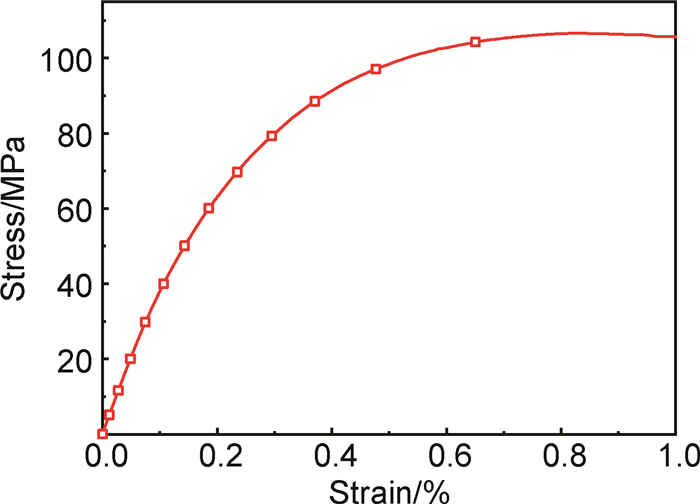
|
图 3 典型剪切应力-应变曲线 Fig. 3 Typical shear stress-strain curve |
实验获得的面内剪切性能数据如表 1所示,强度和模量的均值分别为95.33MPa和33.40GPa,标准差分别为7.28和4.36。为保证数据准确性,用MNR最大赋范残差统计量对异常数据进行定量的筛选。定义最大赋范残差统计量MNR:
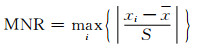
|
(1) |
式中:xi为样本观测值;x为样本平均值;S为样本方差,与之对应的临界值C可由下式计算:
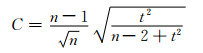
|
(2) |
式中:t为自由度n-2的t分布的1-α/(2n)概率函数值。将MNR与临界值进行比较,如果MNR大于临界值C,则剔除可疑数据,否则,应该保留该数据。
由式(1)计算可得面内剪切强度性能MNR=1.7349,模量性能MNR=2.0871,由式(2)可得当n=30时,最大赋范残差检查方法临界值C=2.908,模量和强度两项性能异常数据检查结果均满足MNR < C,说明30组数据均正常,不存在异常数据。
| Property | Strength/MPa | Modulus/GPa |
| Mean value | 95.33 | 33.40 |
| Stdev | 7.28 | 4.36 |
| MNR | 1.7349 | 2.0871 |
材料性能统计分布规律的研究本质为基于实验数据进行的非参数检验。可分为两步:首先,用线性回归方法对材料性能服从不同分布的参数进行估计,然后结合Kolmogrov检验对材料性能分布进行假设检验。
威布尔分布、正态分布、对数正态分布的概率密度函数如式(3)~(5)所示:
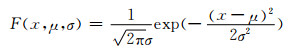
|
(4) |
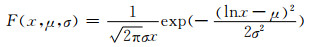
|
(5) |
式中:α为Weibull分布的尺度参数;β为形状参数,可以作为衡量数据分散性的指标;μ,σ分别为正态分布和对数正态分布中的均值和标准差,这些都为估计参数。以Weibull函数为例,在式(3)的基础上,对函数变形得到1-F(x, α, β)=exp(-[(x/α)β]),并且等式两边同时取对数,将得到一个Y=BX+A形式的等式:
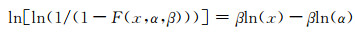
|
(6) |
可得Y=ln[ln(1/(1-F(x, α, β)))],X=lnx, A=-βlnα,B=β。以(x, Y)=(ln(xi), ln[ln(1/(1-S))])为数据对,由式(6)可以得直线方程,进而由直线斜率和截距与待估计参数之间的转换关系求出参数。3种分布的线性回归变换关系如表 2所示[19]。
| Distribution | X | Y | A | B |
| Weibull | lnx | ln[ln(1/(1-F(x)))] | -β lnα | β |
| Normal | x | Φ-1(F(x)) | -(μ/σ) | 1/σ |
| Lognormal | lnx | Φ-1(F(x)) | -(μ/σ) | 1/σ |
式(6)中F(x, α,β)未知,用实验数据估计的经验失效概率S代替。将实验所得数据从小到大排序,并依次编号为1, 2…30,S代表在一定应力水平下失效的经验概率,但是同样对于陶瓷基材料,对于经验失效概率S的使用存在分歧,有如下两种定义[3-4, 6, 19]:
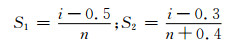
|
(7) |
同时计算两种不同定义的经验失效概率S1和S2,对比两者的差异是否对参数估计有影响。线性回归分析结果如图 4所示。
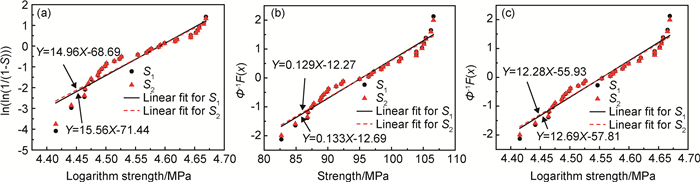
|
图 4 线性回归分析结果 (a)Weibull分布;(b)正态分布;(c)对数正态分布 Fig. 4 Result of linear regression analysis (a)Weibull distribution; (b)normal distribution; (c)lognormal distribution |
图 4(a),(b),(c)分别为对强度的线性回归分析,依次为Weibull分布、正态和对数正态分布。图中不同形状分散点分别代表用式(7)中两种不同定义的经验失效概率得出的(X, Y)数据对,两条直线分别是对两组数据对的线性拟合结果,每条直线对应的直线方程也在图中给出。由表 2中直线方程系数与3种分布参数之间的转换关系,得到参数估计的结果,如表 3所示。
| Parameter | Strength/MPa | Modulus/GPa | ||||||
| Weibull | Normal | Lognormal | Weibull | Normal | Lognormal | |||
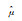 or or 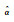
|
S1 | 98.62 | 95.41 | 4.56 | 40.02 | 37.85 | 3.63 | |
| S2 | 98.64 | 95.11 | 4.55 | 40.26 | 37.88 | 3.63 | ||
| Error/% | 0.02 | 0.31 | 0.22 | 0.60 | 0.08 | 0 | ||
 or or  |
S1 | 15.56 | 7.52 | 0.079 | 9.11 | 5.10 | 0.136 | |
| S2 | 14.96 | 7.75 | 0.081 | 8.73 | 5.29 | 0.141 | ||
| Error/% | 3.86 | 3.06 | 2.53 | 4.17 | 3.73 | 3.68 | ||
由表 3参数估计结果可以看出:用式(7)中两种不同定义的经验失效概率S1和S2对材料性能服从不同分布进行参数估计时,μ(α)的相对误差非常小,除模量对Weibull分布α的估计误差为0.6%之外,其余情况两者的相对误差均小于0.1%;对参数σ(β)的估计相对误差在4%左右。
2.3.2 假设检验Kolmogrov检验用于检验经验分布是否服从于某种理论分布。设(X1, X2…Xn)是取自具有连续分布函数F(x)的一个样本,欲假设检验设:
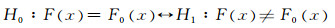
|
(8) |
其中不等号至少对某一点成立。检验采用统计量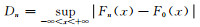
对材料性能分布规律的假设检验同样涉及对经验失效概率的使用,因此,将采用式(7)中的S1和S2作为两个经验失效概率,与通过两个不同的经验失效概率得出的估计参数对应的理论累积概率相结合,对2D-C/SiC复合材料面内剪切性能服从的分布规律进行假设检验。这样,不仅可以确定材料性能的分布规律,也可以研究使用不同的经验失效概率对假设检验结果是否产生影响。使用经验失效概率S1对面内剪切强度服从Weibull分布的假设检验及结果如表 4所示。
| Strength/MPa | S1 | SW | Dn |
| 92.4 | 0.4500 | 0.3043 | 0.1457 |
由表 4可知Dn= |SW-S1| =0.1457,不等式Dn= |SW-S1| =0.1457≤D30, 0.05=0.2417成立,所以采用经验失效概率S1对面内剪切强度服从Weibull分布的假设检验结果表示接受假设H0:F(x)=F0(x),即认为强度服从Weibull分布。采用两个不同经验失效概率S对强度和模量分别服从3种不同分布(Weibull、正态和对数正态)假设检验的统计量Dn如表 5所示。
| Property | S1 | S2 | |||||
| Weibull | Normal | Lognormal | Weibull | Normal | Lognormal | ||
| Strength | 0.1457 | 0.1099 | 0.1227 | 0.1371 | 0.0930 | 0.0960 | |
| Modulus | 0.0891 | 0.0814 | 0.0775 | 0.0990 | 0.0740 | 0.0720 | |
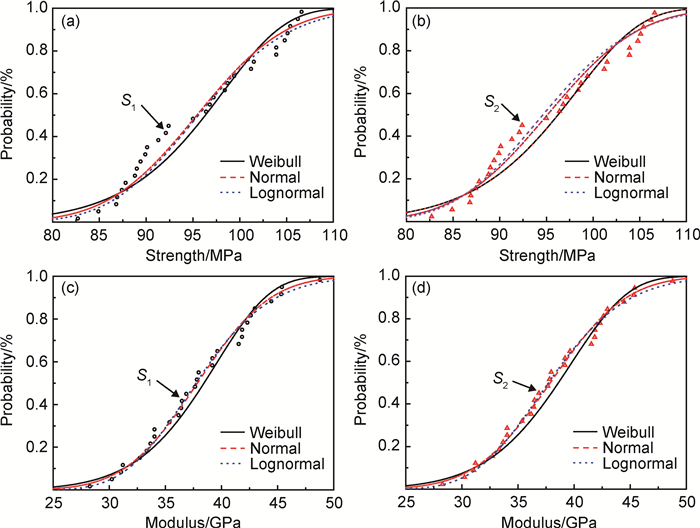
由表 5可知,依据S1或S2计算得出的统计量Dn均满足Dn≤D30, 0.05=0.2417,即使用两种不同的经验失效概率对材料性能分布规律的假设检验结论是相同的:2D-C/SiC复合材料面内剪切强度同时服从Weibull分布、正态分布和对数正态分布,模量也同时服从上述3种分布。说明采用不同的经验失效概率S对于材料性能分布规律假设检验会产生定量误差,但不影响定性分析结果。3种不同分布理论累积概率曲线和经验失效概率点拟合情况如图 5所示。
|
图 5 理论概率-经验概率拟合图 (a)强度经验概率S1;(b)强度经验概率S2;(c)模量经验概率S1;(d)模量经验概率S2 Fig. 5 Fitting curves of theoretical and empirical probability (a)strength empirical probability S1; (b)strength empirical probability S2; (c)modulus empirical probability S1; (d)modulus empirical probability S2 |
图 5(c),(d)面内剪切模量得出的经验失效概率与理论累积概率拟合图,分散点大多位于正态分布和对数正态分布曲线上,说明使用这两种分布拟合2D-C/SiC复合材料面内剪切模量分布规律更合适。
2D-C/SiC复合材料面内剪切性能分布规律以及参数已经确定,将表 3参数估计结果带入式(3), (4), (5),可以得到材料性能分布的理论模型。强度实验数据均值为95.33MPa,模量实验数据均值为37.94GPa。Weibull分布、正态分布、对数正态分布的均值计算公式如下:
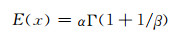
|
(9) |
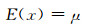
|
(10) |
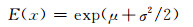
|
(11) |
式中:Γ为伽马函数,α,β,μ,σ均使用估计值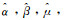
| Property | Weibull | Normal | Lognormal | |||||
| S1 | S2 | S1 | S2 | S1 | S2 | |||
| Strength/MPa | 95.34 | 95.26 | 95.41 | 95.11 | 95.88 | 94.94 | ||
| Modulus/GPa | 37.92 | 38.07 | 37.85 | 37.88 | 38.06 | 38.09 | ||
| Note:Experimental strength is 95.33MPa; experimental modulus is 37.94MPa | ||||||||
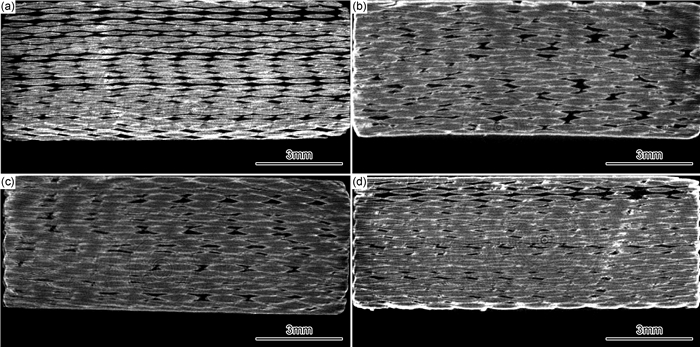
图 6为2D-C/SiC复合材料面内剪切强度服从Weibull分布的概率密度曲线,在曲线上选择A, B, C, D 4个点,分别对应强度为84.9, 92.1, 98.7, 106.6MPa的面内剪切试样。对初始状态最窄净截面微CT扫描照片和断口电镜照片进行观察,分析导致2D-C/SiC复合材料面内剪切强度分散性的微观机制。

|
图 6 Weibull分布概率密度曲线 Fig. 6 Curve of Weibull probability density |
图 7为试样初始状态最窄净截面微CT扫描照片。从图 7(a)~(d)致密度逐渐增大,强度也随之增大。致密度反映了基体的沉积效果。致密度高,基体沉积较多,可以增加有效承载面积,承担更大的载荷;更多的基体可以增强层间性能,并且支撑保护纤维束,从而发挥纤维束承担载荷的更大性能;还可以填补纤维以及纤维束间的孔洞,避免孔洞尖端应力集中而引起的损伤扩展。由图 7(a)可见,材料致密度低,基体对纤维束保护支撑弱,所以强度较低;由图 7(d)可见,材料致密度较高,孔洞少,可避免由孔洞尖端引起的应力集中导致损伤扩展。综上,最窄净截面致密度是造成2D-C/SiC复合材料剪切强度分散性的重要原因,但并不代表致密度始终与强度呈正比关系。
|
图 7 试件横截面微CT扫描照片 (a)84.9MPa;(b)92.1MPa;(c)98.7MPa;(d)106.6MPa Fig. 7 μ-CT scanning photographs of cross section of the specimens (a)84.9MPa; (b)92.1MPa; (c)98.7MPa; (d) 106.6MPa |
界面性能是影响2D-C/SiC复合材料面内剪切强度的重要因素,它的直接表现为界面脱粘长度。界面摩擦力可以由公式[20]:τ=λ(m)·σcritical·R/L估计,式中:λ(m)为拔出系数;σcritical为纤维的特征应力;L是平均纤维拔出长度;R为纤维直径。界面摩擦力τ与纤维拔出平均长度L成反比。图 8依次为图 6中A, B, C, D4个点对应试样的界面脱粘长度电镜照片,可见,随着强度的增大,界面脱粘长度逐渐减小, LA>LB>LC>LD,与理论结果相吻合。
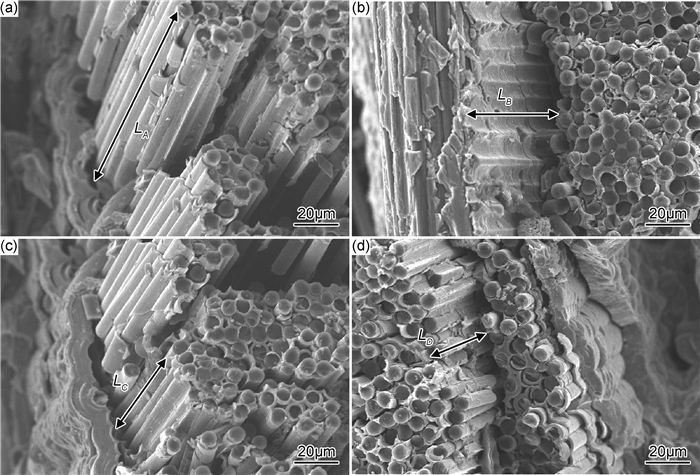
|
图 8 界面脱粘长度SEM照片 (a)84.9MPa;(b)92.1MPa;(c)98.7MPa;(d)106.6MPa Fig. 8 SEM photographs of the interface debonding length (a)84.9MPa; (b)92.1MPa; (c)98.7MPa; (d)106.6MPa |
B基准值的定义为:建立在统计学上的衡量材料性能的参数,在95%置信度下,90%的性能数值群高于此值。依照复合材料手册MIL-HDBK-17提供的方法,如果Weibull分布能恰当的拟合数据则推荐使用该模型,即使其他模型显得拟合的更好。前文通过假设检验已得出2D-C/SiC复合材料面内剪切强度同时服从Weibull分布、正态分布和对数正态分布。所以在计算2D-C/SiC复合材料面内剪切强度B基准值时优先使用Weibull模型。Weibull模型B基准值计算公式为:
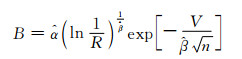
|
(12) |
式中:R=0.9;n为样本数, 此处n=30;V是威布尔分布单侧B基准值容限系数,当n=30时,V=5.057;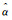
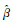
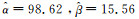
(1) 2D-C/SiC复合材料强度不仅服从Weibull分布,也同时服从于正态分布和对数正态分布;模量也同时服从于上述3种分布,但与正态分布和对数正态分布的契合程度优于Weibull分布。
(2) 两种不同的经验失效概率对于检验材料性能分布规律存在定量计算上的差异,但不影响定性分析。在参数估计中,对μ(α),σ(β)以及统计量Dn的计算存在偏差,但最终结果保持一致。两种不同经验失效概率得出的理论模型预测均值与实验数据均值十分吻合。
(3)通过观察材料最窄净截面微CT扫描照片和断口电镜扫描照片,发现最窄净截面致密度越高,材料剪切强度越大;界面脱粘长度越短,剪切强度越大。
(4)依照复合材料手册MIL-HDBK-17提供的B基准值计算方法,计算得到2D-C/SiC复合材料面内剪切强度的B基准值为B=80.41MPa。
| [1] | NASLAIN R, GUETTE A, REBILLATE F, et al. Boron-bearing species in ceramic matrix composites for long-term aerospace applications[J]. Journal of Solid State Chemistry, 2004, 177 (2): 449–456. DOI: 10.1016/j.jssc.2003.03.005 |
| [2] | NASLAIN R. Design, preparation and properties of non-oxide CMCs for application in engines and nuclear reactors:an overview[J]. Composites Science and Technology, 2004, 64 (2): 155–170. DOI: 10.1016/S0266-3538(03)00230-6 |
| [3] |
严科飞, 张程煜, 乔生儒, 等. C/C复合材料室温面内剪切强度分布[J].
机械强度, 2012, 34 (6): 912–915.
YAN K F, ZHANG C Y, QIAO S R, et al. Statistical distribution on in-plane shear strength of C/C composite at room temperature[J]. Journal of Mechanical Strength, 2012, 34 (6): 912–915. |
| [4] |
李辉, 张立同, 曾庆丰, 等. 2D C/SiC复合材料的可靠性评价[J].
复合材料学报, 2007, 24 (4): 95–100.
LI H, ZHANG L T, ZENG Q F, et al. Reliability analysis of 2D-C/SiC composite[J]. Acta Materiae Compositae Sinica, 2007, 24 (4): 95–100. DOI: 10.3321/j.issn:1000-3851.2007.04.017 |
| [5] |
童小燕, 张凯, 姚磊江, 等. 2D C/SiC复合材料蠕变寿命分布规律研究[J].
机械强度, 2013, 35 (6): 823–828.
TONG X Y, ZHANG K, YAO L J, et al. Investigation for creep life distribution of 2D C/SiC composites[J]. Journal of Mechanical Strength, 2013, 35 (6): 823–828. |
| [6] |
吴守军, 成来飞, 董宁, 等. 3D Hi-Nicalon/SiC复合材料室温三点弯曲强度分布[J].
复合材料学报, 2005, 22 (5): 130–133.
WU S J, CHENG L F, DONG N, et al. Flexural strength distribution of 3D Hi Nicalon/SiC in three point bending test at room temperature[J]. Acta Materiae Compositae Sinica, 2005, 22 (5): 130–133. DOI: 10.3321/j.issn:1000-3851.2005.05.021 |
| [7] | LIU Y, CHENG L, ZHANG L, et al. Fracture behavior and mechanism of 2D C/SiC-BCx composite at room temperature[J]. Materials Science and Engineering:A, 2011, 528 (3): 1436–1441. DOI: 10.1016/j.msea.2010.10.045 |
| [8] | LIU Y, CHAI N, QIN H, et al. Tensile fracture behavior and strength distribution of SiCf/SiC composites with different SiBN interface thicknesses[J]. Ceramics International, 2015, 41 (1): 1609–1616. DOI: 10.1016/j.ceramint.2014.09.098 |
| [9] | PITT R E, PHOENIX S L. Probability distributions for the strength of composite materials IV:localized load-sharing with tapering[J]. International Journal of Fracture, 1983, 22 (4): 243–276. DOI: 10.1007/BF01140156 |
| [10] | CALARD V, LAMON J. A probabilistic-statistical approach to the ultimate failure of ceramic-matrix composites-part Ⅰ:experimental investigation of 2D woven SiC/SiC composites[J]. Composites Science & Technology, 2002, 62 (3): 385–393. |
| [11] | CALARD V, LAMON J. A probabilistic statistical approach to the ultimate failure of ceramic-matrix composites-part Ⅱ:macroscopic model[J]. Composites Science & Technology, 2002, 62 (3): 395–399. |
| [12] | GENET M, COUEGNAT G. Scaling strength distributions in quasi-brittle materials from micro-to macro-scales:a computational approach to modeling nature-inspired structural ceramics[J]. Journal of the Mechanics and Physics of Solids, 2014, 68 (1): 93–106. |
| [13] | RICHTER H, PETERS P W M. Tensile strength distribution of all-oxide ceramic matrix mini-composites with porous alumina matrix phase[J]. Journal of the European Ceramic Society, 2016, 13 (36): 3185–3191. |
| [14] |
马鑫, 关志东, 薛斌, 等. 复合材料B基准值计算程序[J].
制造业自动化, 2011, 33 (21): 83–87.
MA X, GUAN Z D, XUE B, et al. Programming of B-basis value calculation of composite[J]. Manufacturing Automation, 2011, 33 (21): 83–87. DOI: 10.3969/j.issn.1009-0134.2011.11(s).23 |
| [15] |
董本正, 李伟, 高丽红, 等. 基于Matlab的碳纤维复合材料的B基准值算法[J].
现代电子技术, 2014 (16): 87–91.
DONG B Z, LI W, GAO L H, et al. Matlab-based algorithm for B reference value of carbon fiber reinforced polymer[J]. Modern Electronics Technique, 2014 (16): 87–91. DOI: 10.3969/j.issn.1004-373X.2014.16.026 |
| [16] |
王翔, 陈新文, 王海鹏, 等. 基于统计的复合材料B基准值计算方法研究[J].
失效分析, 2010, 5 (4): 210–215.
WANG X, CHEN X W, WANG H P, et al. Statistic-based calculation methods of B-basis value of composite[J]. Failure analysis and Prevention, 2010, 5 (4): 210–215. DOI: 10.3969/j.issn.1673-6214.2010.04.004 |
| [17] |
刘新, 王荣国, 刘文博, 等. 三角形截面碳纤维复合材料弯曲强度B基准值[J].
宇航学报, 2010, 31 (6): 1651–1655.
LIU X, WANG R G, LIU W B, et al. The B-basis value of the flexural strength of triangle-shape carbon fibers reinforced plastics[J]. Journal of Astronautics, 2010, 31 (6): 1651–1655. DOI: 10.3873/j.issn.1000-1328.2010.06.023 |
| [18] |
管国阳, 矫桂琼, 张增光. 平纹编织C/SiC复合材料的剪切性能[J].
机械科学与技术, 2005, 24 (5): 515–517.
GUAN G Y, JIAO G Q, ZHANG Z G. In-plane shear fracture characteristic of plain woven C/SiC composite[J]. Mechanical Science and Technology, 2005, 24 (5): 515–517. DOI: 10.3321/j.issn:1003-8728.2005.05.003 |
| [19] |
赵永翔, 孙亚芳, 高庆. 分析常用7种统计分布的统一线性回归方法[J].
机械强度, 2001, 23 (1): 102–106.
ZHAO Y X, SUN Y F, GAO Q. Unified linear regression method for the analysis of seven commonly used statistical distributions[J]. Journal of Mechanical Strength, 2001, 23 (1): 102–106. DOI: 10.3321/j.issn:1001-9669.2001.01.028 |
| [20] | YAN K F, ZHANG C Y, QIAO S R, et al. In-plane shear strength of a carbon/carbon composite at different loading rates and temperatures[J].2011, 528(3): 1458-1462. https://www.researchgate.net/publication/241099787_In-plane_shear_strength_of_a_carboncarbon_composite_at_different_loading_rates_and_temperatures |
 2019, Vol. 47
2019, Vol. 47


