文章信息
- 许善迎, 谭焕成, 关玉璞, 刘璐璐
- XU Shan-ying, TAN Huan-cheng, GUAN Yu-pu, LIU Lu-lu
- 三维四向编织复合材料力学性能预测及实验验证
- Predication and Experimental Verification on Mechanical Properties of Three-dimensional and Four-direction Braided Composites
- 材料工程, 2018, 46(6): 132-140
- Journal of Materials Engineering, 2018, 46(6): 132-140.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.001135
-
文章历史
- 收稿日期: 2016-09-21
- 修订日期: 2017-09-27
三维编织复合材料是将纤维束经一定的编织工艺技术形成预编织件,然后与基体材料固化成型得到的。三维编织技术起源于20世纪60年代,目前常用的制备工艺有:四步法编织、二步法编织和实体编织技术。其中四步法编织于1982年由Florentine[1]发明出来,该项编织技术得到最广泛的应用。基于编织工艺规律以及编织物真实细观结构,一些学者针对编织物的细观结构和几何建模进行了大量分析和研究。Ko[2]首次用一个四角交叉纤维束的正方体对矩形编织预制体的纤维结构进行描述。由于该模型描述过于简单,Wu[3]和Wang等[4-5]对三维编织预制件进行了拓扑分析,把结构定义为可区分的内部、表面和棱角处三种单胞组成。对于三单胞模型的选取,目前主流有两种划分方案[6]:水平划分法和45°划分法,其中45°单胞划分方案中只适用于主纤维束行列数均为偶数情况,若其中有一个为奇数,该划分方法就不能使宏观结构完全地包含三种单胞,而是在角处出现多余的正方形部分。研究者[7-9]利用有限元软件对三维编织过程进行模拟,并建立相关实体模型,或者建立起细观编织结构和编织参数之间的关系,并给出了相应的数学公式[6, 10]。
目前学者获得三维编织物弹性常数的方法主要有三种:理论计算、数值分析以及实验测试。在理论分析方面,主要有刚度平均化方法[11-12]和均匀化理论[13],这些方法主要基于纤维束和基体力学性能通过计算和转换对整个编织体的弹性常数进行预测。在数值分析方面,一些学者利用有限元软件ANSYS, ABAQUS等对单胞模型或预制体细观结构模型进行数值分析,预测整个编织体的弹性常数。在实验方面,文献[14-16]中主要开展三维编织物的拉伸、压缩、剪切等实验,获得三维编织物的弹性常数。
大部分学者仅从理论计算、数值仿真以及实验三种方法中三选二或三选一研究编织复合材料刚度特性。本工作不仅从理论计算、数值仿真以及实验三个方面研究三维编织复合材料弹性常数随编织角变化规律,还对现有文献中纤维束不同截面形状假设对纤维体积含量的影响进行对比与总结,同时指出了三维编织复合材料应力应变曲线随编织角的变化趋势。本工作理论计算采用刚度平均化方法,不仅将其应用于内胞模型,还应用于面胞模型;数值分析方法则利用ABAQUS软件不仅在内胞分析时施加了周期性边界条件,还在对面胞进行刚度分析时,利用编写的Python程序,在与相邻面胞接触的两个面亦施加了周期性边界条件。
1 刚度平均化方法三维四向编织复合材料由纤维束和基体组成。在预测其弹性常数时,一般认为纤维束是线弹性、横观各向同性材料,树脂基体是线弹性、均匀各向同性材料。刚度平均化方法具体思路是将各个方向局部坐标系下纤维束的刚度矩阵通过应力转换矩阵转换为整体坐标系下的刚度矩阵,然后和基体的刚度矩阵基于单胞中各组分材料的体积含量进行刚度平均求和,得到整体坐标系下单胞的刚度矩阵,求逆得到整体坐标系下单胞的柔度矩阵,进而得到整体坐标系下单胞的弹性常数。图 1为刚度平均化方法预测内胞和面胞弹性性能的编程思路流程图。

|
图 1 预测内胞和面胞弹性常数的编程思路流程图 Fig. 1 Flow diagram of programming idea for predicting elastic constants of interior cell and surface cell |
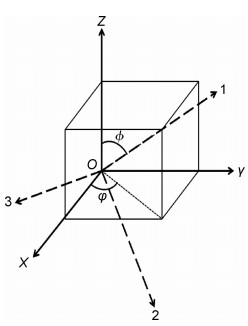
如图 2所示,设定总体坐标系O-XYZ,纤维束局部坐标系O-123,总体坐标系中Z轴为编织方向轴,在局部坐标系中1轴为单向纤维束主轴。局部坐标系中1轴、2轴、3轴相对于总体坐标系X轴、Y轴、Z轴的方向余弦分别为l1,m1,n1,l2,m2,n2,l3,m3,n3,相应关系和表达式见表 1。
|
图 2 坐标系转换 Fig. 2 Coordinate systems transformation |
| Coordinates | 1 | 2 | 3 |
| X | l1 | n1 | m1 |
| Y | l2 | n2 | m2 |
| Z | l3 | n3 | m3 |
表 1中:l1=sin(ϕ)cos(φ), m1=sin(φ), n1=cos(ϕ)cos(φ), l2=sin(ϕ)sin(φ), m2=-cos(φ), n2=cos(ϕ)sin(ϕ), l3=cos(φ), m3=0, n3=-sin(φ), φ=45°。
可知应力转换矩阵为:
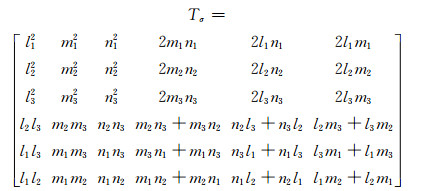
|
局部坐标系下刚度矩阵和整体坐标系下刚度矩阵之间关系为:
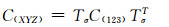
|
(1) |
得到纤维束在整体坐标下的刚度矩阵后,根据内部单胞中纤维束和基体的体积含量以及刚度矩阵,可以得到内部单胞的刚度矩阵Cn,见式(2):
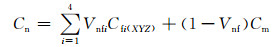
|
(2) |
式中:Cm为基体的刚度矩阵;Vnfi表示第i种方向纤维在内部单胞中体积含量; Vnf为所有纤维束在内部单胞中体积含量,且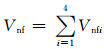
对于内胞和面胞中纤维束的分析,唯一区别在于,内胞中16根纤维束在空间走向都是直线,有4种空间角度,而面胞中采用文献[17]的处理结果,面部区域中纤维束在空间走向为折线,有8种空间角度,具体见表 2。
| Type | Space angle coordinate of yarn |
| Interior cell | (±γ,±φ) |
| Surface cell | (±γ,±φ)(±θ,±φ) |
表 2中第一个坐标表示纤维束与编织方向(Z轴正方向)的夹角,即图 2中的ϕ,第二个坐标表示纤维束在XY的投影与X轴正方向的夹角,即图 2中的φ,γ为内部编织角,θ为面部编织角,它们与编织角α之间的关系为
| Braiding angle/(°) | Surface braiding angle/(°) | Internal braiding angle/(°) |
| 20 | 9.7 | 27.2 |
| 30 | 15.2 | 39.2 |
| 45 | 25.2 | 54.7 |
得到内胞和面胞在整体坐标系下的刚度矩阵,根据实验件中内胞和面胞所含的体积含量,加权求和(见式(3)),可以预测实验件的弹性常数。
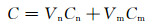
|
(3) |
式中:Vn为编织物中内部单胞占实验件的体积分数;Vm为编织物中面部单胞占实验件的体积分数;Cm为面胞的刚度矩阵。
实验件材料选取天津工业大学研制的三维四向碳纤维/环氧编织复合材料,预成型件采用三维四向1×1四步法编织制造,通过RTM工艺固化成型,编织物中纤维体积分数61%~62%。增强纤维为12K-T700碳纤维,基体为TED-86环氧树脂。细观组分材料的性能参数见表 4。根据文献[18]以及厂家提供的m和n值可以计算出厚度为4mm,编织角为20°,30°,45°实验件的内胞体积分数和面胞体积分数,见表 5。
| T700-12K Yarn | TDE-86 Epoxy resin | |||
| Item | Value | Item | Value | |
| Longitudinal tensile elastic modulus/GPa | 230 | Elastic modulus/GPa | 3.45 | |
| Longitudinal compressive elastic modulus/GPa | 130 | Poisson’s ratio | 0.35 | |
| Transverse elastic modulus/GPa | 15 | Density/(g·cm-3) | 1.19 | |
| Longitudinal shear modulus/GPa | 20 | |||
| Longitudinal Poisson’s ratio | 0.28 | |||
| Transverse Poisson’s ratio | 0.4 | |||
| Ultimate tensile strength/MPa | 4900 | |||
| Cross sectional area/mm2 | 0.44 | |||
| Density/(g·cm-3) | 1.76 | |||
| Braiding angle/(°) | m | n | Volume fraction of interior cell/% | Volume fraction of surface cell/% |
| 20 | 5 | 152 | 33.63 | 66.37 |
| 30 | 5 | 142 | 33.65 | 66.35 |
| 45 | 5 | 115 | 33.72 | 66.28 |
经过编程计算,得到编织角为20°,30°,45°三维四向编织复合材料内胞和面胞以及加权求和后预测的弹性常数,具体结果见表 6。
| Parameter | 20° | 30° | 45° | ||||||||
| Interior cell | Surface cell | Weighted mean value | Interior cell | Surface cell | Weighted mean value | Interior cell | Surface cell | Weighted mean value | |||
| EX/GPa | 14.950 | 13.191 | 14.355 | 18.910 | 9.713 | 15.844 | 25.850 | 11.882 | 19.522 | ||
| EY/GPa | 14.950 | 13.191 | 14.355 | 18.910 | 9.713 | 15.844 | 25.850 | 11.882 | 19.522 | ||
| EZ/GPa | 86.940 | 108.17 | 93.327 | 51.460 | 41.336 | 46.605 | 25.850 | 25.755 | 28.806 | ||
| GYZ/GPa | 20.200 | 16.996 | 19.123 | 22.900 | 9.974 | 18.551 | 20.780 | 9.750 | 15.655 | ||
| GZX/GPa | 20.200 | 16.996 | 19.123 | 22.900 | 9.974 | 18.551 | 20.780 | 9.750 | 15.655 | ||
| GXY/GPa | 6.890 | 5.476 | 6.415 | 11.590 | 4.667 | 9.261 | 20.780 | 7.469 | 15.214 | ||
| μYZ | 0.540 | 0.453 | 0.510 | 0.501 | 0.440 | 0.488 | 0.311 | 0.357 | 0.353 | ||
| μXZ | 0.540 | 0.453 | 0.510 | 0.501 | 0.440 | 0.488 | 0.311 | 0.357 | 0.353 | ||
| μXY | 0.298 | 0.351 | 0.314 | 0.260 | 0.360 | 0.281 | 0.311 | 0.367 | 0.323 | ||
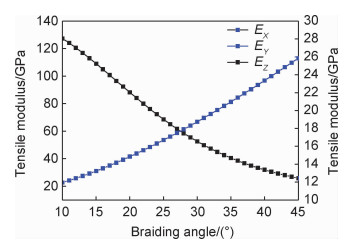
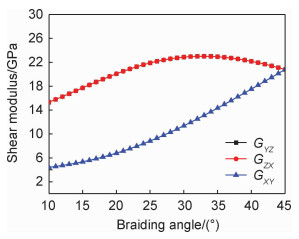
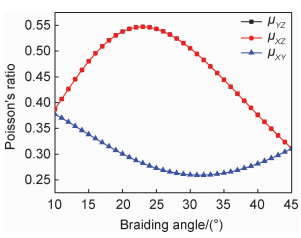
对于大厚度的编织复合材料,编织物内的内胞含量至少超过60%,因此可以用内胞的弹性常数反映整个编织体的弹性常数。图 3,4,5分别是根据内胞模型得到三维四向编织材料拉伸弹性模量、剪切模量以及泊松比随编织角的变化规律,纤维体积分数取62%。可以看出:(1)随着编织角α的增加,EZ逐渐减小,EX,EY,GXY逐渐增加,主要原因是α增大,纤维束在Z轴方向刚度分量逐渐减小,在X,Y方向刚度分量逐渐增加;(2)随着α的增加,GYZ,GZX先增大后减小,在32°附近取得最大值,这是因为随着编织角的增加,X,Y方向纤维束的增强作用一直增加,而Z方向的增强作用逐渐减少。当试件编织角达到一定角度时,沿着横向的变形达到最大,而随着编织角继续增加,试件的横向变形逐渐降低。(3)μYZ,μXZ先增大后减小,在23°附近取得最大值,这是因为随着编织角的增加,受纤维束空间位置的影响,试件三个方向的变形逐渐增大,但X,Y方向变形的增加趋势更大。在编织角达到一定角度时,X,Y方向的变形和Z方向变形的比值达到最大,此时纵向泊松比达到最大值。随着编织角度继续增加,试件X,Y方向变形受纤维束的约束而逐渐减小,泊松比逐渐降低,这使得纵向泊松比先增加后减小。同理,μXY先减小后增大,在30°附近取得最小值。
|
图 3 内胞模型的拉伸弹性模量随编织角变化曲线 Fig. 3 Curves of tensile modulus of interior cell with change of braiding angle |
|
图 4 内胞模型的剪切模量随编织角变化曲线 Fig. 4 Curves of shear modulus of interior cell with change of braiding angle |
由于编织复合材料细观结构的复杂性,现有有限元分析工作通常忽略材料外部区域面胞、角胞的影响,假设材料横截面尺寸足够大,研究占材料主体的内胞的力学行为来表征整个结构的力学性能。
表 7为纤维束在不同截面形状假设下计算所得的纤维体积分数,从表中可以看出,圆形截面假设对应的纤维体积分数最小,六边形截面下的编织物纤维最大体积分数最大。根据天津工业大学提供的三维四向碳/环氧编织复合材料拉伸实验件,编织物中纤维体积分数61%~62%,可知八边形截面假设下,编织物纤维体积含量最接近实验件的纤维体积含量,再结合文献[19]介绍和分析,本工作将采用受挤压纤维束的截面为八边形的假设。此外八边形截面的单胞模型在有限元网格划分中要比圆形截面和椭圆截面要容易一些。
| Section shape | Maximum fill factor of fiber in yarn | Fiber volume fraction ininterior cell/% | Fiber volume fraction insurface cell/% | Volume fraction of interior cell in weave/% | Volume fraction of surface cell in weave/% | Fiber volume fraction of weave /% |
| Circular | 0.78 | 40 | 40 | 66.3 | 33.7 | 31.2 |
| Ellipse | 0.75 | 68 | 68 | 51 | ||
| Hexagon | 0.91 | 75 | 75 | 68.25 | ||
| Octagon | 0.89 | 73 | 73 | 64.97 |
本工作基于内胞和面胞模型,利用HYPERMESH软件对其进行周期性网格划分(其中面胞模型仅在与相邻面胞接触两个面进行周期性网格划分),然后在ABAQUS软件中施加周期性边界条件,分别对内胞和面胞进行弹性常数预测。
以20°编织角的内胞为例,在HYPERMESH软件中对内胞进行网格划分时,对于周期性网格,必须保证主从面上网格节点数目和位置分布完全一致,采用面网格复制的方法来实现。本工作对纤维束和基体采用四面体单元进行离散,内胞模型由28450个单元,5870个节点组成,如图 6所示。

|
图 6 20°编织物内胞有限元模型 Fig. 6 Finite model of interior cell in weave(20°) |
在ABAQUS软件中利用基于Python软件编写的程序对单胞施加周期性边界条件[20-22],然后对纤维束和基体分别添加材料属性、截面属性,考虑到内胞中的纤维束有4种空间方向主轴,对相应的纤维束添加相应的材料轴局部坐标系。然后分别施加6种基于简单应变的方程边界条件(εX0, εY0, εZ0, γXY0, γXZ0, γYZ0,设定其应变值为0.01),基于单胞的应力和变形形态,确定其弹性常数。
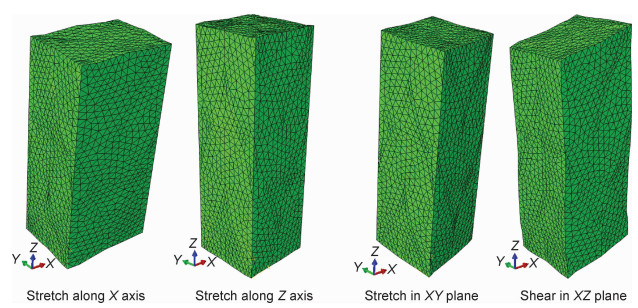
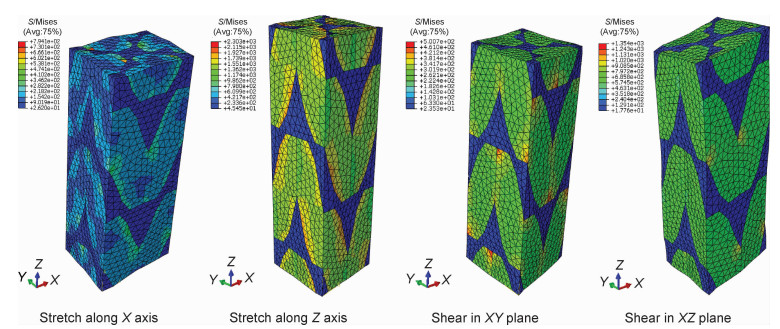
由于三维四向编织复合材料纤维束空间结构的轮换特征,单胞模型在X拉伸和Y拉伸、XZ剪切和YZ剪切载荷下变形和应力分布具有相似性,以下仅给出X拉伸、Z拉伸、XY剪切及XZ剪切4种载荷下的分析结果。
从图 7单胞变形状态可以看出,相对两个面变形一致或保持常值,变形连续,单胞受载后保持了其在空间上的周期性。从图 8单胞应力状态可以看出,在各种载荷下,单胞模型中纤维束应力均明显大于基体,承受着主要载荷,这主要是由纤维束的刚度远大于基体,载荷按刚度分配决定的。但是,在不同应变载荷工况下,纤维束的承载机理并不相同,所以单胞模型的力学响应特征也不同。
|
图 7 内胞模型在不同载荷下的变形 Fig. 7 Deformation condition of interior cell under different loads |
|
图 8 内胞模型不同载荷下的应力分布 Fig. 8 Stress distribution of interior cell under different loads |
表 8为数值计算得到20°,30°,45°编织角内胞和面胞及其加权求和的弹性常数。
| Parameter | 20° | 30° | 45° | ||||||||
| Interior cell | Surface cell | Weighted mean value | Interior cell | Surface cell | Weighted mean value | Interior cell | Surface cell | Weighted mean value | |||
| EX/GPa | 12.786 | 6.835 | 11.436 | 16.001 | 7.625 | 12.721 | 22.171 | 9.713 | 19.405 | ||
| EY/GPa | 12.786 | 9.665 | 11.999 | 16.001 | 11.171 | 13.034 | 22.171 | 12.235 | 19.970 | ||
| EZ/GPa | 107.000 | 38.055 | 93.643 | 54.017 | 33.317 | 45.673 | 21.242 | 18.978 | 23.278 | ||
| GYZ/GPa | 21.334 | 4.051 | 17.514 | 27.509 | 4.186 | 20.906 | 24.336 | 2.402 | 19.455 | ||
| GZX/GPa | 21.334 | 3.035 | 17.302 | 27.509 | 2.837 | 20.621 | 24.336 | 1.789 | 19.337 | ||
| GXY/GPa | 6.396 | 0.658 | 5.139 | 12.368 | 0.833 | 9.179 | 24.229 | 1.120 | 19.124 | ||
| μYZ | 0.697 | 0.816 | 0.711 | 0.643 | 0.360 | 0.522 | 0.375 | 0.140 | 0.346 | ||
| μXZ | 0.697 | 0.898 | 0.724 | 0.643 | 0.463 | 0.571 | 0.375 | 0.208 | 0.358 | ||
| μXY | 0.356 | 0.252 | 0.338 | 0.318 | 0.107 | 0.214 | 0.342 | 0.165 | 0.336 | ||
根据GB/T 1447-2005纤维增强塑料拉伸性能实验方法, 标准设计厚度为4mm、编织角为20°, 30°, 45°的拉伸实验件,拉伸实验件的设计方案如图 9所示,对于纵向拉伸实验件采用Ⅱ型试样,横向拉伸实验件采用Ⅰ型试样(厂家提供的编织物平板尺寸限制,故选用Ⅰ型),鉴于横向拉伸实验件Ⅰ型尺寸较小,故在拉伸实验中应变率采用1×10-5 s-1,而纵向拉伸实验件Ⅱ型尺寸较大,故纵向拉伸应变率采用1×10-4 s-1。由于3D编织复合材料的各向异性,测试其面内性质时,分别进行纵向拉伸实验和横向拉伸实验,实验所用设备为MTS793拉压和疲劳试验机。

|
图 9 纵横向拉伸实验件设计(a)横向拉伸实验件;(b)纵向拉伸实验件 Fig. 9 Design of longitudinal and transverse tensile tests (a)transverse tensile test; (b)longitudinal tensile test |
对实验后的数据进行处理,发现编织角20°编织复合材料试样的纵向拉伸应力应变曲线近似弹性,在最终断裂前显示出弱的屈服;编织角30°编织复合材料试样的纵向拉伸应力应变曲线,相对于20°,30°编织复合材料试样的纵向拉伸应力应变显示出明显非线性;编织角45°编织复合材料试样的纵向拉伸呈现双线性。
对于纵向拉伸,随着编织角增大,可以发现应力应变曲线由线弹性、弱屈服转换为非线性,进而转化为双线性;而对于横向拉伸,应力应变曲线基本呈现线弹性,45°时应力应变曲线略呈非线性。
随着编织角增大,实验件应力应变曲线发生变化的原因,分析如下:(1)实验件是在编织体中切割加工而成的,切割边缘导致实验件中部分纤维变成短纤维,编织角越大,实验件中纤维越短。(2)对于纵向拉伸过程,刚开始时,由纤维和基体共同承受作用力,由于纤维和基体在受力下变形的差异,随后部分纤维与基体界面发生脱胶,编织角较小时,界面脱胶并不剧烈,纤维和基体呈脆性断裂,纤维在纵向拉伸方向分量较大,纵向刚度较大;编织角较大时,短纤维与拉伸方向夹角较大,纤维在纵向拉伸方向分量较小,纵向刚度较小,由于大编织角的实验件的短纤维较多,脱胶的纤维较多,因而后续承受力主要是剩余基体和少量的纤维,因而应力应变关系逐渐呈现双线性;总体来说,随着编织角增大,编织复合材料的破坏从脆性破坏转向延性破坏。(3)对于横向拉伸过程,拉伸方向与编织方向垂直,且实验件宽度较纵向拉伸实验件宽度小,从而在拉伸过程中,纤维脱胶明显,主要是基体和少量的短纤维承受拉力,因此应力应变曲线呈现线弹性断裂,当编织角增大,纤维束的纵向刚度在横向分量增加,从而实验件横向刚度增加。
表 9和表 10分别是实验得到弹性模量和泊松比。表 9和表 10中实验件的代号意义:ST表示静态拉伸,ST后面数字为编织角,L表示纵向,T表示横向。
| Number of experimental samples | Strain rate/s-1 | Modulus of elasticity/GPa | Average value/GPa | Variance |
| ST20_L_1 | 1×10-4 | 98.10 | 94.75 | 11.2225 |
| ST20_L_2 | 1×10-4 | 91.40 | ||
| ST30_L_1 | 1×10-4 | 40.90 | 43.25 | 5.5225 |
| ST30_L_2 | 1×10-4 | 45.60 | ||
| ST45_L_1 | 1×10-4 | 26.10 | 25.40 | 0.2500 |
| ST45_L_2 | 1×10-4 | 25.30 | ||
| ST45_L_3 | 1×10-4 | 24.90 | ||
| ST20_T_1 | 1×10-4 | 8.32 | 8.56 | 0.0576 |
| ST20_T_2 | 1×10-4 | 8.80 | ||
| ST30_T_1 | 1×10-5 | 10.09 | 10.15 | 0.2100 |
| ST30_T_2 | 1×10-5 | 9.62 | ||
| ST30_T_3 | 1×10-5 | 10.74 | ||
| ST45_T_1 | 1×10-5 | 14.13 | 15.41 | 0.8400 |
| ST45_T_2 | 1×10-5 | 16.24 | ||
| ST45_T_3 | 1×10-5 | 15.86 |
| Number of experimental samples | Strain rate/s-1 | Poisson’s ratio | Average value | Variance |
| ST20_L_1 | 1×10-4 | 0.889 | 0.787 | 0.0100 |
| ST20_L_2 | 1×10-4 | 0.685 | ||
| ST30_L_1 | 1×10-4 | 0.588 | 0.703 | 0.0130 |
| ST30_L_2 | 1×10-4 | 0.818 | ||
| ST45_L_1 | 1×10-4 | 0.514 | 0.480 | 0.0006 |
| ST45_L_2 | 1×10-4 | 0.472 | ||
| ST45_L_3 | 1×10-4 | 0.454 |
基于实验数据可以得到不同编织角下刚度参数,并与理论计算和数值分析结果进行比较,见表 9。由表 9可知,理论计算和数值分析在实验件编织方向(Z轴方向)刚度的预测精度较高,对实验件横向刚度预测精度比较差,预测值比实验值大,究其原因主要是无论是理论计算还是数值仿真都忽略了纤维与基体在实验件受拉伸过程中发生的脱胶现象,在横向拉伸中由于实验件宽度较小,在拉伸过程中,主要靠基体和短纤维承载,纤维与基体之间界面开裂非常明显。至于泊松比,实验测得泊松比受应变片粘贴位置的影响,可能贴在纤维上、基体上或纤维与基体交汇处,在拉伸过程中,贴片处的纤维出现抽拔或断裂以及基体开裂等现象影响,导致实验测得泊松比仅是实验件局部的泊松比而非整个实验件的泊松比,因此误差较大,实验测得泊松比普遍偏大。从表 11中也可以看出弹性常数随编织角变化趋势,随着编织角的增大,编织方向的刚度减小,横向刚度增大,与图 5中相应参数随编织角的变化趋势吻合。
|
图 5 内胞的泊松比随编织角变化曲线 Fig. 5 Curves of Poisson's ratio of interior cell with change of braiding angle |
| Parameter | 20° | 30° | 45° | ||||||||
| Experiment | Theoretical calculation | Numerical analysis | Experiment | Theoretical calculation | Numerical analysis | Experiment | Theoretical calculation | Numerical analysis | |||
| EX/GPa | 8.560 | 14.355 | 11.436 | 10.150 | 15.844 | 12.721 | 15.41 | 19.522 | 19.400 | ||
| EY/GPa | 14.355 | 11.999 | 15.844 | 13.034 | 19.522 | 19.961 | |||||
| EZ/GPa | 94.750 | 93.327 | 93.643 | 43.250 | 46.605 | 45.673 | 25.40 | 28.806 | 20.251 | ||
| GYZ/GPa | 19.123 | 17.514 | 18.551 | 20.906 | 15.655 | 19.455 | |||||
| GZX/GPa | 19.123 | 17.302 | 18.551 | 20.621 | 15.655 | 19.337 | |||||
| GXY/GPa | 6.415 | 5.139 | 9.261 | 9.179 | 15.214 | 19.124 | |||||
| μYZ | 0.510 | 0.711 | 0.488 | 0.522 | 0.353 | 0.338 | |||||
| μXZ | 0.787 | 0.510 | 0.724 | 0.703 | 0.488 | 0.571 | 0.48 | 0.353 | 0.352 | ||
| μXY | 0.314 | 0.338 | 0.281 | 0.214 | 0.323 | 0.335 | |||||
(1) 理论计算发现,随着编织角增大,三维四向编织复合材料纵向刚度减小,横向刚度增大,横向剪切模量增加,这是因为编织角增大,纤维束在纵向分量减小,在横向分量增大。三维四向编织复合材料纵向剪切模量先增大后减小,在32°附近取得最大值,横向泊松比先减小后增大,在30°附近取得最小值,纵向泊松比先增大后减小,在23°附近取得最大值。
(2) 在数值分析中,基于纤维束截面形状的分析,圆形截面假设对应的编织物纤维体积分数最小,六边形截面假设下的编织物纤维最大体积分数最大,其中八边形截面假设最适合用来预测本工作选取实验件的弹性常数。
(3) 基于内胞和面胞模型,刚度平均化方法和数值分析方法在预测三维编织复合材料纵向刚度方面精确度较高,但在横向刚度方面预测精度较差,究其原因是忽略了纤维与基体脱胶现象。
(4) 20°编织角纵向拉伸应力应变曲线基本呈线弹性,30°纵向拉伸应力应变曲线呈现非线性,45°纵向拉伸应力应变曲线呈现双线性。随着编织角增大,编织复合材料的破坏从脆性破坏转向延性破坏。20°, 30°, 45°横向拉伸应力应变曲线基本呈线性。
| [1] | FLORENTINE R. Apparatus for weaving a three-dimensional article: US 4. 312. 261[P]. 1982-01-26. |
| [2] | KO F K. Three dimensional fabrics for composites: an introduction to the magnaweave structure[R]. Tokyo: Proceeding of the ICCM-4 Japan Society Composite Material, 1982. |
| [3] | WU D L. Three-cell model and braided structural composites[J]. Composites Science and Technology, 1996, 56 : 225–233. DOI: 10.1016/0266-3538(95)00136-0 |
| [4] | WANG Y Q, WANG A S D. Microstructure-property relationships in 3-D braided composites[J]. Composites Science Technology, 1995, 53 : 213–222. DOI: 10.1016/0266-3538(95)00021-6 |
| [5] | WANG Y Q, WANG A S D. Geometric mapping of yarn structures in 3D braided composites due to shape change[J]. Composites Science Technology, 1995, 53 : 359–370. |
| [6] | CHEN L, TAO X M, CHO C L. On the microstructure of three-dimensional braided performs[J]. Composites Science and Technology, 1999, 59 : 391–404. DOI: 10.1016/S0266-3538(98)00079-7 |
| [7] | ZHOU G M, SUN X K, WANG Y Q. Multi-chain digital element and analysis in textile mechanics[J]. Composites Science and Technology, 2004, 64 : 239–244. DOI: 10.1016/S0266-3538(03)00258-6 |
| [8] |
寇晓菲. 三维编织复合材料编织工艺过程仿真研究[D]. 武汉: 华中科技大学, 2012. KOU X F. Simulation research on the braiding process of 3D braided composites[D]. Wuhan: Huazhong University of Science and Technology, 2012. |
| [9] |
王毅强, 张立同, 成来飞. 三维编织体复合材料空间几何结构的计算机模拟[J].
航空材料学报, 2008, 28 (2): 95–98.
WANG Y Q, ZHANG L T, CHENG L F. Computer geometry simulation of spatial structure of three-dimensional braided composites[J]. Journal of Aeronautical Material, 2008, 28 (2): 95–98. |
| [10] | LI D, CHEN L, LI J. Microstructure and unit-cell geometry of four-step three-dimensional rectangular braided composites[J]. Journal of Reinforced Plastics & Composites, 2010, 29 (22): 3353–3363. |
| [11] | DONG W, ZHU J, TANG Y, et al. Property research of tensile elasticity for three-dimensional braiding composite material[J]. Cotton Textile Technology, 2016 (4): 24–27. |
| [12] | NI C, WEI G. Geometric model and elastic constant prediction of 3D four-step braided composites based on the cubic spline curve[J]. International Journal of Applied Mechanics, 2016, 8 (2): 1650019. DOI: 10.1142/S1758825116500198 |
| [13] |
董纪伟. 基于均匀化理论的三维编织复合材料宏细观力学性能的数值模拟[D]. 南京: 南京航空航天大学, 2007. DONG J W. Homogenization-based method for simulating macro and micro mechanical properties of 3D braided composites[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. |
| [14] | LU Z X, QI H U. Experimental investigation into the compressive mechanical properties of three dimensional braided composites[J]. Acta Materiae Compositae Sinica, 2003, 20 (6): 67–72. |
| [15] |
李苏红. 三维编织复合材料的拉伸性能及破坏模式[D]. 上海: 东华大学, 2014. LI S H. Tensile properties and failure modes of three dimensional braided composites[D]. Shanghai: Donghua University, 2014. |
| [16] |
李翠敏, 阎建华, 刘丽芳, 等. 三维编织碳纤维复合材料剪切性能研究[J].
纤维复合材料, 2014 (2): 45–49.
LI C M, YAN J H, LIU L F, et al. Shear properties of three dimensional braided carbon fiber composites[J]. Fiber Composites, 2014 (2): 45–49. |
| [17] |
张超. 三维多向编织复合材料宏细观力学性能及高速冲击损伤研究[D]. 南京: 南京航空航天大学, 2013. ZHANG C. Research on macro-meso-mechanical properties and high velocity impact damage of 3D multi-directional braided composites[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. |
| [18] |
梁军, 方国东.
三维编织复合材料力学性能分析方法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
LIANG J, FANG G D. Method of mechanical properties analysis of 3D braided composites[M]. Harbin: Harbin Institute of Technology Press, 2014. |
| [19] | FANG G D, LIANG J, WANG Y, et al. The effect of yarn distortion on the mechanical properties of 3D four-directional braided composites[J]. Composites:Part A, 2009, 40 (4): 343–350. DOI: 10.1016/j.compositesa.2008.12.007 |
| [20] | XIA Z H, ZHANG Y F, ELLYIN F. A unified periodical boundary conditions for representative volume elements of composites and applications[J]. International Journal of Solids and Structures, 2003, 40 (8): 1907–1921. DOI: 10.1016/S0020-7683(03)00024-6 |
| [21] | LI S G, WONGSTO A. Unit cells for micromechanical analyses of particle-reinforced composites[J]. Mechanics of Materials, 2004, 36 (7): 543–572. DOI: 10.1016/S0167-6636(03)00062-0 |
| [22] | LI S G. Boundary conditions for unit cells from periodic microstructures and their implications[J]. Composites Science Technology, 2008, 68 (9): 1962–1974. DOI: 10.1016/j.compscitech.2007.03.035 |
 2018, Vol. 46
2018, Vol. 46


