文章信息
- 周钰博, 李艳霞, 李敏, 顾轶卓, 张佐光, 宋永忠, 余立琼, 程家
- ZHOU Yu-bo, LI Yan-xia, LI Min, GU Yi-zhuo, ZHANG Zuo-guang, SONG Yong-zhong, YU Li-qiong, CHENG Jia
- 细编穿刺织物的数学建模理论与实例
- Theory and Examples of Mathematical Modeling for Fine Weave Pierced Fabric
- 材料工程, 2017, 45(4): 102-107
- Journal of Materials Engineering, 2017, 45(4): 102-107.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.000479
-
文章历史
- 收稿日期: 2015-04-23
- 修订日期: 2016-10-08
2. 航天材料及工艺研究所, 北京 100076
2. Aerospace Research Institute of Materials & Processing Technology, Beijing 100076, China
细编穿刺织物是一种三维立体织物,与其他织物相比[1],厚度方向纤维含量很高,因而在厚度方向具有独特的性能,常作为C/C复合材料的增强体[2, 3],用于飞机刹车装置、火箭耐高温部件等处。细编穿刺织物的加工工艺复杂,成本高,通过建模仿真方法预测其力学及物理特性[4](如渗透率等) 具有重要的意义。目前,针对细编穿刺织物,仅在1~2束纤维的亚单胞尺度有数学模型的报道[5],由于其损失了织物的周期性结构,无法考虑到纤维滑动等因素,模拟仿真的准确性受到影响,而在单胞及若干的单胞的较大尺度上,未见有仿真模型的报道,仅有抽象结构模型[4]。本工作针对细编穿刺织物,建立了一种准确度较高的数学抽象与织物结构数学建模方法,可同时用于小尺度的亚单胞模型与大尺度的宏观模型分析,具有较高的适应性。
织物结构建模可以上溯到20世纪30年代,Peirce[6]提出经典的平纹织物的几何模型,其将丝束的截面假定为椭圆形,并用丝束屈曲高度、丝束几何密度、丝束纺织角等参数描述织物的模型。近年来,随着预成型体编织技术和液体成型工艺的发展,预成型体织物结构的数字化、模型化受到关注。基于单胞模型的各项研究得到展开,如三维立体织物的结构优化设计[7]与预成型体中纤维弯曲对复合材料性能的影响分析[8, 9];基于含有若干单胞的三维缝合织物的模型,采用计算流体力学和有限元方法,预测三维缝合织物层内的渗透率[10, 11]与预成型体的拉伸性能[10];采用有限单元方法,预测预成型体的导电性与导热性[12],液体成型过程中预成型体受力分析[13],基于单胞模型的预成型体纤维体积分数和厚度预测[14-16]等。与传统的跑道型建模方法[15]不同,本工作采用具有参数连续性的样条线建立细编织物穿刺织物单胞模型,同时,对比了不同丝束截面与轨迹特性所建立织物数学模型,通过丝束结构与孔隙率的对比,织物数学模型与织物真实结构具有较好的符合性,为细编穿刺织物的渗透率预测及液体成型工艺模拟提供技术基础。
1 数学建模用织物样例采用的细编穿刺织物由南京玻璃纤维研究院生产,纤维型号为T700碳纤维,通过Skyscan 1076 MicroCT获取的断面图如图 1所示。织物参数为:Z向纤维束直径0.603 mm±0.031 mm,XY向纤维束高0.280 mm±0.023 mm,XY向纤维束宽0.575 mm±0.046 mm,孔隙率为46.67%。

|
图 1 细编穿刺织物的MicroCT照片 Fig. 1 MicroCT photo of fine weave pierced fabric |
对于细编穿刺织物进行三维仿真建模,需将织物进行数学抽象,提取出织物的丝束轨迹特性与截面特性,再将截面特性与丝束轨迹特性结合,获得丝束实体或表面的特性。针对细编穿刺织物,本文的织物仿真模型精确到丝束级别,总尺度为若干个丝束,为编织结构的若干个单胞组合。
2.1 丝束轨迹特性为了定义丝束的轨迹,将三维丝束实体抽象为一维丝束的中心线,通过设定丝束中心线通过的“特殊点”(即丝束在织物中的“结点”),运用数学插值的方法,实现丝束中心线的连续性模拟。
丝束的中心线是一条光滑、连续的曲线,其函数表达需要满足至少一阶参数连续性,因此,采用“样条线”来对丝束的中心线进行拟合。样条线是通过指定点的拟合曲线,对其进行描述的插值函数具有定义域上的连续性。样条线方程通常用分段多项式方程来描述,对于一条定义域为[a, b]的样条线,典型方程形式如下:
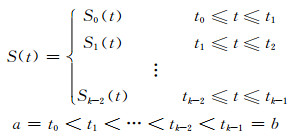
|
(1) |
其中,给定k值,ti点为样条线的结点,也是丝束在织物中的结点,Si (t) 为样条线的分段。
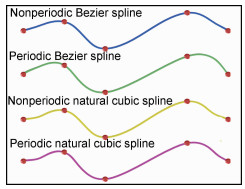
本工作考虑了两类四种样条线:周期性与非周期性贝塞尔样条线 (具有一阶参数连续性)、周期性与非周期性自然立方样条线 (具有二阶参数连续性)。为了避免龙格现象,样条线的分段参数方程采用三阶:
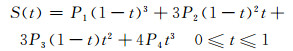
|
(2) |
贝塞尔样条线的分段是按照零阶连续性和一阶连续性定义的,按照样条线结点要求,有:
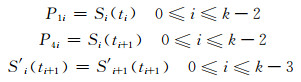
|
(3) |
且满足:
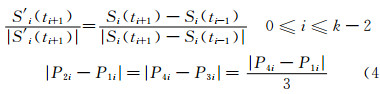
|
(4) |
在样条线两端 (t=a与t=b) 满足
(1) 若丝束不具有周期性,有:
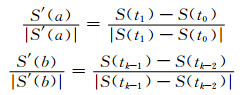
|
(5) |
结合式 (3) 和 (4),就得到了 (非周期性) 贝塞尔样条线。
(2) 若丝束是周期性的,满足:

|
(6) |
结合式 (3) 和 (4),就得到了周期性贝塞尔样条线。
通常采用贝塞尔样条线的模型与真实情况符合较好,同时在特殊情况下,通过提供特定的定义点使曲线更符合真实的丝束路径。
2.1.2 自然立方样条线的参数定义与贝塞尔样条线相似,通过样条线零阶、一阶与二阶参数连续性能得出以下方程:
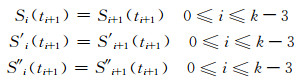
|
(7) |
对于自然立方样条线,要求使得以下函数值最小:
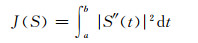
|
(8) |
函数J (S) 的意义是样条线S (t) 的总曲率。因为自然立方样条线的物理模型是弹性绳 (样条线) 在若干个固定点 (样条线结点) 的约束下处于总能量最低的状态,因此要使得样条线具有最低的总曲率。
(1) 若丝束不具有周期性,则在样条线端头处 (t=a与t=b),满足:

|
(9) |
结合式 (7) 和 (8),就得到了 (非周期性) 自然立方样条线。
(2) 若针对织物的单胞建模,丝束具有周期性,则在样条线端头处 (t=a与t=b),满足:
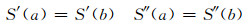
|
(10) |
结合式 (7) 和 (8),就得到了周期性自然立方样条线。由于S′(tk-1)=S′(t0),周期性自然立方样条线的方程比 (非周期性) 自然立方样条线少一个。
由于在样条线两端具有相同的一阶与二阶导数,周期性自然立方样条线能够非常好的适应织物结构单元的建模,在结构单元重复堆积的地方,能够同时满足零阶、一阶与二阶参数连续性,因此对于织物重复单元建模有着重要的意义。
四种样条线的对比如图 2所示。
|
图 2 四种样条线的对比 Fig. 2 Comparison of four kinds of spline |
丝束的横截面是二维的平面图形,所在平面与丝束中心线垂直。丝束是含有若干单丝的三维实体,其横截面为垂直于丝束中心线,能包含所有纤维的最小平面区域。由于真实丝束的横截面外凸且边缘不光滑,在建模中需将横截面的最小区域的边缘光滑化,在满足精确性与便捷性的同时做出近似。
通常,丝束的横截面有两种近似:幂次椭圆与透镜形。
2.2.1 幂次椭圆截面幂次椭圆截面是椭圆形截面的一种修正,通过一个幂次参数n对椭圆在高度h上进行修正,n越小,横截面越接近于矩形,n越大,横截面越接近于透镜形,当幂次系数n=1时,幂次椭圆还原为普通椭圆,如图 3(a)所示。其数学表达式如下:
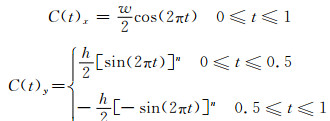
|
(11) |

|
图 3 幂次椭圆 (a) 与透镜形 (b) 示意图 Fig. 3 Power ellipse (a) and lenticular (b) |
透镜形截面是半径为r1与r2的两个圆在垂直方向上各自偏移o1与o2所相交形成的,参数r1,r2,o1,o2可以通过截面的宽w、高h以及透镜形截面的扭曲距离d计算而得,解析表达式为:
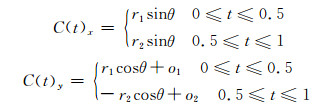
|
(12) |
其中
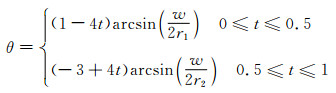
|
(13) |
图 3(b)所示是三种典型的透镜形,其中,当透镜形截面的扭曲距离d为0,两个圆的半径相同,偏移距离大小相同,方向相反。
2.3 丝束实体与表面特性根据数学理论,由丝束中心线和丝束横截面方程即可确定丝束的三维结构,但在实际建模中,需要绘制丝束实体或表面的三维图形,而数学抽象的横截面,是零厚度的二维平面,若简单地将丝束中心线与丝束横截面简单合并起来,需要无数横截面堆叠,此时数据量巨大。为简化模型的建立,利用丝束的特性,将建模需要的横截面减少为有限个。
沿着丝束的中心线方向,丝束的横截面是一个光滑变化的图形,即丝束的横截面是一个沿着丝束中心线变化的函数。固丝束实体可以定义为一个关于丝束路径S与丝束横截面C的函数P (u, v):
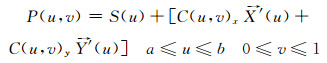
|
(14) |
其中,

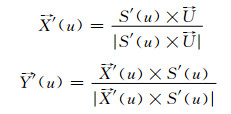
|
(15) |
定义



|
图 4 建模坐标系 Fig. 4 Coordinate system of modeling |
在参数表面的函数P (u, v) 的定义式中,横截面C由两个参数确定,分别为变量u与变量v,其中,u代表的是横截面与丝束中心线的交点在中心线上的位置,v代表的是横截面上的位置。
由于丝束的横截面是一个不断变化的图形,所以采用关键点与关键面的方法简化建模:离散地在丝束的中心线上定义一些关键点,在关键点上定义该点的横截面 (关键面),在关键点之间采用插值运算的方法,补充横截面,生成丝束的外表面。通常关键点为丝束中心线 (样条线) 的结点,为了提高精确度,关键点也可以为任意点。当丝束的横截面变化非常小时,可只在每条丝束中心线上定义一个关键面,简化建模,提高运算性能。
采用如下的插值方法:若A (t) 与B (t) 为定义在关键点上的关键面,则A (t) 与B (t) 之间的一个插值面C (t) 满足:
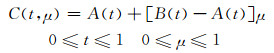
|
(16) |
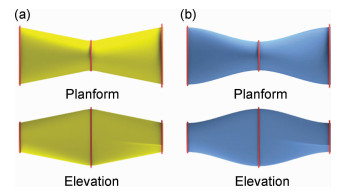
式中μ的值从0到1线性变化,代表插值面C (t) 在关键点A (t) 与B (t) 之间线性变化。这种线性插值同时适用于相同与不同类型的截面,并生成满足零阶参数连续性的光滑过度表面。如图 5(a)所示,图中显示了线性插值的截面变化情况。模型从左到右,关键面分别为横向放置的长轴长2单位、短轴长1单位的椭圆形截面,纵向放置的长轴长2单位、短轴长1单位的椭圆形截面以及横向放置的长2单位、高1单位、扭曲距离为-0.25单位的透镜型截面。
|
图 5 截面插值示意图 (a) 线性插值;(b) 平滑修正后的插值 Fig. 5 Sketch of section interpolation (a) linear interpolation; (b) interpolation after smooth |
线性插值通常与实际情况存在着较大的偏差,如在关键点处出现截面的突变,即截面不满足一阶参数连续性。可以通过适当的平滑修正,改变μ与丝束位置d的线性相关性,修正以上缺陷。可使用三次等式修正,使得在关键点处满足:
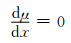
|
(17) |
即有
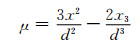
|
(18) |
基于细编穿刺织物的数学抽象模型,即可按照一定的方法与手段建立织物的三维数字模型。
分别按照两种截面,四种丝束轨迹特性曲线进行建模。其中,采用椭圆形截面、周期性贝塞尔样条线的织物模型的透视图如图 6所示。

|
图 6 采用椭圆形截面、周期性贝塞尔样条线的织物模型的透视图 Fig. 6 Scenograph of models with ellipse section and periodic Bezier spline |
对比八种模型的几何结构,由于建模所选取的区域为织物编织结构的单胞,已具有一定的周期重复性,因此对于同一种丝束轨迹的插值方法,样条线的周期性与否,对几何上的影响并不明显,同时,由于丝束轨迹与丝束截面在数学处理上相对独立,不同的截面形状并不影响丝束的轨迹。以透镜形截面为例,对比周期性贝塞尔样条线与自然立方样条线,如图 7所示,可以明显看出,在紧邻弯折区域的结点附近 (圆圈处),自然立方样条线出现了明显的屈曲,而贝塞尔样条线的屈曲幅度很小,这是由于自然立方样条线所具有二阶参数连续性而引起的。

|
图 7 周期性贝塞尔样条线 (a) 与自然立方样条线 (b) 的区别 Fig. 7 Difference of periodic Bezier spline (a) with periodic natural cubic spline (b) |
将采用椭圆形截面、周期性贝塞尔样条线的织物模型的断面图 (如图 8) 与真实织物获取的断面图 (图 1) 进行比较,可以发现,在排除因为三维编织造成的织物不规则变形之后,建立的模型与真实模型符合较好。

|
图 8 采用椭圆形截面、周期性贝塞尔样条线的织物模型的断面图 Fig. 8 Sectional view of models with ellipse section and periodic Bezier spline |
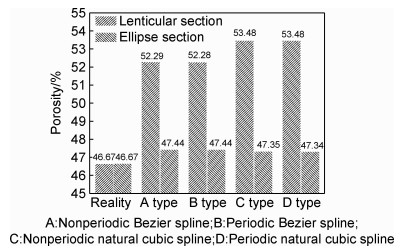
基于上述八种织物模型,进一步计算了预成型的孔隙率如图 9所示。由图 9计算数据对比可知:(1) 与透镜形截面的织物模型相比,椭圆形截面模型的孔隙率较低且与穿刺织物的孔隙率更接近,表明穿刺织物的丝束截面更接近于椭圆形;(2) 同一种样条线,周期性与非周期性的差别很小,这是由于织物的特性所决定的;(3) 对比真实织物与模型孔隙率,模型的孔隙率也均高于真实织物。
|
图 9 不同模型的孔隙率及其与实际值的比较 Fig. 9 Comparison of porosities from different models and with reality |
孔隙率误差主要由三个方面产生:(1) 穿刺织物在制备过程中,由于外力作用,纤维出现大量的变形与损伤,织物整体呈现受挤压状态[5],破损的纤维填充了相当量的孔隙,导致纤维的有序性降低,丝束的规则性下降,造成孔隙率偏差;(2) 模型将丝束作为一个整体处理,仅考虑了束间孔隙,从而造成孔隙率偏差;(3) 数学模型的特征尺寸和结构特性来自于真实织物的测量,同时,模型中丝束的截面与轨迹特性也需要近似化处理,因此,实验测量和数学近似都会造成数学抽象与真实情况之间的误差,固需要采取多重测量,以及采取多种近似方法进行建模,从中选取最合理的方案,减小误差。
4 结论(1) 与传统的跑道型轨迹模型相比,本工作中采用的贝塞尔样条线与自然立方样条线轨迹模型的出发点是丝束的参数连续性。相对于只具有零阶参数连续性的跑道型轨迹模型,贝塞尔样条线与自然立方样条线轨迹模型分别具有一阶和二阶参数连续性,因而其更接近于自然状态下的织物,建立的模型更符合真实的丝束状态。
(2) 以细编穿刺三维立体织物为样例,本工作分别建立了基于两种典型截面、四种轨迹样条线的八种模型,并将它们的孔隙率与真实织物的实测孔隙率进行比较,发现模型与真实织物的孔隙率数据吻合较好,说明所建立的数学模型抽象与建模方法能够较好地描述织物的真实状况,为穿刺织物渗透率及力学性能等参数预测提供了重要基础。
(3) 该织物微观结构建模方法也可用于其他类型的2D,2.5D及3D织物等预成型体的抽象建模,并可用于预成型体的渗透率、导电性、导热性等物理性能以及力学性能的预测与分析,可以提高针对预成型体相关性能研究的效率,降低研究的成本。
| [1] | 于倩倩, 陈刚, 郑志才. 缝合技术在复合材料上的应用及研究进展[J]. 工程塑料应用, 2009, 37 (5): 85–88. YU Q Q, CHEN G, ZHENG Z C. Application and review of research in stiching technology for composites[J]. Engineering Plastics Application, 2009, 37 (5): 85–88. |
| [2] | 朱建勋. 细编穿刺织物的结构特点及性能[J]. 宇航材料工艺, 1998 (1): 41–43. ZHU J X. The structural characteristics and properties of fine weave pierced fabric[J]. Aerospace Materials & Technology, 1998 (1): 41–43. |
| [3] | 朱建勋. 碳布整体穿刺织物编织工艺与结构参数优化[D]. 南京: 东南大学, 2003. ZHU J X. The optimization of knitting technology and structure parameters for integrated piercing carbon fabric[D]. Nanjing: Southeast University, 2003. |
| [4] | 方国东, 梁军, 王裕. 利用有限元方法对细编穿刺复合材料进行有效性能预报[C]//第十五届全国复合材料学术会议. 哈尔滨: 中国力学协会, 2008: 1397-1401. FANG G D, LIANG J, WANG Y. The finite element analysis of mechanical properties of fine woven pierced composites [C]//15th National Conference on Composite Materials.Harbin: Chinese Society of Theoretical and Applied Mechanics, 2008:1397-1401. |
| [5] | 陈盛洪. 细编穿刺C/C复合材料热物理性能的模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2008. CHEN S H. Simulation on thermal physical properties of fine weave pierced C/C composite[D]. Harbin: Harbin Institute of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10213-2009290492.htm |
| [6] | PEIRCE F T. The geometry of cloth structure[J]. Journal of the Textile Institute Transactions, 1937, 28 (3): T45–T96. DOI: 10.1080/19447023708658809 |
| [7] | OKUMURA T, YOKOYAMA A, NAGAI K, et al. Optimum design of weaving structure of 3-D woven fabric composites by using genetic algorithms[J]. Composite Structures, 1995, 32 (1-4): 417–426. DOI: 10.1016/0263-8223(95)00084-4 |
| [8] | STIG F, HALLSTR M S. Influence of crimp on 3D-woven fibre reinforced composites[J]. Composite Structures, 2013, 95 : 114–122. DOI: 10.1016/j.compstruct.2012.07.022 |
| [9] | 燕瑛, 成传贤. 基于细观结构的三维机织复合材料弹性性能的分析[J]. 航空学报, 1999, 28 (4): 2–6. YAN Y, CHENG C X. Analysis of elastic property for 3-D woven composites based on fabric microstructure[J]. Acta Aeronautica et Astronautica Sinica, 1999, 28 (4): 2–6. |
| [10] | ZENG X, BROWN L P, ENDRUWEIT A, et al. Geometrical modelling of 3D woven reinforcements for polymer composites: Prediction of fabric permeability and composite mechanical properties[J]. Composites Part A: Applied Science and Manufacturing, 2014, 56 : 150–160. DOI: 10.1016/j.compositesa.2013.10.004 |
| [11] | 杨波, 金天国, 郑龙. 微-细双尺度单胞下织物预成型体渗透率预测[J]. 复合材料学报, 2013, 30 (5): 209–217. YANG B, JIN T G, ZHENG L. Permeability prediction for textile preform with micro-meso dual-scale unit cell[J]. Acta Materiae Compositae Sinica, 2013, 30 (5): 209–217. |
| [12] | SIDDIQUI M O R, SUN D. Finite element analysis of thermal conductivity and thermal resistance behaviour of woven fabric[J]. Computational Materials Science, 2013, 75 : 45–51. DOI: 10.1016/j.commatsci.2013.04.003 |
| [13] | WENDLING A, HIVET G, VIDAL-SALLÉ E, et al. Consistent geometrical modelling of interlock fabrics[J]. Finite Elements in Analysis and Design, 2014, 90 : 93–105. DOI: 10.1016/j.finel.2014.05.010 |
| [14] | 丁辛, 易洪雷. 三维机织几何结构的数值表征[J]. 东华大学学报 (自然科学版), 2003, 29 (3): 15–19. DING X, YI H L. Representation of geometric architecture of three-dimensional woven structures by numerical method[J]. Journal of Donghua University (Natural Science), 2003, 29 (3): 15–19. |
| [15] | 丁辛, 易洪雷. 三维机织结构的几何模型[J]. 复合材料学报, 2003, 20 (5): 108–113. DING X, YI H L. A geometric model of three dimensional woven structures[J]. Acta Materiae Compositae Sinica, 2003, 20 (5): 108–113. |
| [16] | 杨彩云, 李嘉禄. 基于纱线真实形态的三维机织复合材料细观结构及其厚度计算[J]. 复合材料学报, 2005, 22 (6): 178–182. YANG C Y, LI J L. Microstructure and thickness equation of 3D woven composites based on yarn’s true configuration[J]. Acta Materiae Compositae Sinica, 2005, 22 (6): 178–182. |
 2017, Vol. 45
2017, Vol. 45


