文章信息
- 于长清, 余悠然, 赵英民, 谢宁
- YU Changqing, YU Youran, ZHAO Yingmin, XIE Ning
- 石墨热压还原Cu/Cu2O金属陶瓷电导逾渗行为与微观结构分形表征
- Electrical percolation behavior and microstructure fractal characterization of graphite reduced hot-pressing Cu/Cu2O cermet composites
- 材料工程, 2022, 50(1): 154-160
- Journal of Materials Engineering, 2022, 50(1): 154-160.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000988
-
文章历史
- 收稿日期: 2019-10-30
- 修订日期: 2021-02-16
2. 济南大学 山东省建筑材料制备与测试技术重点实验室, 济南 250022
2. Shandong Provincial Key Laboratory of Preparation and Measurement of Building Materials, University of Jinan, Jinan 250022, China
材料组织与性能关系的定量表征一直是科研人员面临的重大挑战之一,而非均质材料的显微组织结构更为复杂,其组织与性能定量关系的建立也更加困难。现有的材料很多都是非均质的,因此,其物理性能与微观结构间关系的定量表征自然成为目前材料学领域非常重要的一个研究方向。其中,导体/绝缘体双相复合材料是具有代表性的非均质材料之一。近些年来,导体/绝缘体双相复合材料的应用日益广泛,比如光热电站的高温换热器[1-2]、航天领域导电部件、轻质电子器件上使用的碳/聚合物[3]和金属/聚合物[4]、固体燃料电池[5-6]、电解铝惰性阳极上使用的金属陶瓷[7-8]以及各种导电薄膜与透明电极[9-10]。这类双相复合材料的特点是,当导通相的体积分数达到某一个临界值(称为逾渗阈值)时,导通相会从孤立的弥散相转变成连续的逾渗(percolation)集团结构,导致材料的宏观性能发生相应的突变。对于性能的转变及材料中非均匀组织的分布,必须借助逾渗理论和分形(fractal)方法才能对其进行定量描述。在导体/绝缘体双相复合材料逾渗体系中,对导通相逾渗行为和分形的研究,计算机计算结果是必不可少的部分。因为在真实材料中,无法通过实验对骨架密度和骨架结构进行表征和验证,所以这部分的定量表征只有通过计算机的计算来实现。在早期的逾渗体系计算机研究中,重点都放在如何通过计算得到精确的逾渗阈值,逾渗临界指数以及分形维数对应于微观结构的定量表征关系。近期的研究重点则是对逾渗体系中导通结构的“最短路径”、骨架结构、骨架密度的计算。
导体/绝缘体双相复合材料的组织表征采用的是分形方法[11-15]。对于逾渗集团,普遍认为D=d-β/υ,其中, D是导通相的分形维数,d是体系的拓扑维数,β和υ分别是无限团聚体和相关长度临界指数。利用标度律,将分形维数和材料的逾渗临界指数联系起来,根据目前的普适值,对于二维情况(d=2),β=5/36,υ=4/3,D=1.9;对于三维情况(d=3),β=0.41,υ=0.88,D=2.5[16]。但是,这个值也和实验值有一定的差别[17-21]。实际材料中,导通相的分形维数会随着导通相结构的变化而变化,而导通相的结构又直接受材料制备工艺因素的影响。目前,人们对随机分布的导体/绝缘体非均质材料导通相结构分形特性的研究尚处于起步阶段,对于分形特性对材料本身性能的影响,无论是从实验上还是从理论上都缺乏相应的基础,尚需进行大量工作。
导体/绝缘体双相复合材料在目前的新能源、新材料体系中的应用非常广泛,从材料工程的角度来看,如何将双相复合材料的微观结构和性能间的关系进行定量表征具有十分重要的科学意义。本工作采用石墨热压还原法制备Cu/Cu2O金属陶瓷复合材料,通过测量Cu/Cu2O金属陶瓷的直流电导率,分析其电逾渗与分形行为,并为导体/绝缘体双相复合材料中随机分布的导电相微观结构定量表征提供一种计算方法。该方法将有助于建立导通相微观结构与宏观性能之间的定量关系,进而实现对第二相随机分布的复合材料进行性能预测。
1 实验材料与方法 1.1 分形维数计算方法对采用不同制备方法得到的材料的导通相进行分形维数计算。在MATLAB上计算导通相的二维记盒分形维数(box counting dimension)。采用针对第二相分形维数计算的通用方法,即记盒维数计算法,分别计算具有不同的导通相尺寸、形貌以及网络结构的材料的导通相分形维数。首先,将边长为ε的正方形网格覆盖边长为L的整个图像,其中ε=L/2n(n为大于1的自然数)。其次,计算网格中有像素的方格数目,不论有多少像素,只要有像素点就计数为N(ε),例如,得到N(L/2)= 22,N(L/4)=42,N(L/8)=60 < 82。最后,不断减小网格的边长ε,计算对应的含有像素的网格数N(ε),直到最小的网格尺寸达到像素点为止。将这一系列N(ε)数据作lnN(ε)-ln(1/ε)图,如果能得到一条直线,说明N(ε)和ε有下列关系:
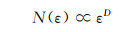
|
(1) |
式中:N(ε)为有像素点的记盒数量;ε为用于记盒的正方盒子边长;D为图像的二维记盒分形维数。
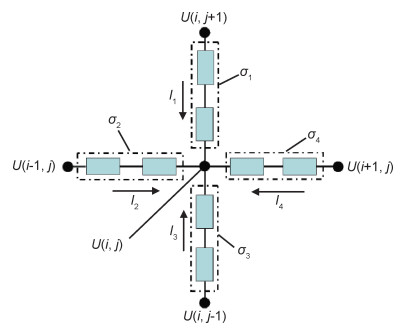
1.2 逾渗行为计算方法图 1给出了二维正方晶格的电流、电压节点示意图。其中U(i, j)为该节点处的电压,σa(a=1~4)为被填充网格的电导率,Ia(a=1~4)为各方向通往节点(i, j)处的电流。在m×n的二维正方晶格中,任选一个节点(i, j), 与其周围四个配位点(i, j+1),(i, j-1),(i+1, j)和(i-1, j)的电导率分别为σi, j,σi, j+1,σi, j-1,σi+1, j和σi-1, j。选定一个体积分数,然后随机填充相应体积分数的二维网格,指定被填充网格的电导率为σa,未被填充的网格电导率为σb(σa=1,σb=10-8)。根据相应的边界条件计算各个节点的电压分布,然后计算各个节点的电流分布。实际计算采用1000×1000的网格,设定导通节点最小电流I=10-6,即当节点上电流大于10-6时,此节点处于导通状态,否则为不导通状态。
|
图 1 二维正方晶格电流、电压节点示意图 Fig. 1 Schematic diagram of the electric voltage and current for 2D square lattice nodes |
本工作中的Cu/Cu2O金属陶瓷复合材料都是通过石墨还原热压法制备获得。Cu2O粉末,分析纯,江苏泰兴粉末公司提供;石墨粉,哈尔滨石墨公司提供。热压还原法制备Cu/Cu2O金属陶瓷的工艺过程:将不同体积分数的石墨粉和Cu2O粉在行星球磨机上球磨24 h,球料比为3 ∶1,球磨介质为无水乙醇。球磨结束后,将混合粉末在烘干炉中烘干,然后放入石墨磨具中进行热压。为了让还原反应充分进行,热压过程中在600 ℃时保温1 h,然后继续升温至1050 ℃,升温速度为20 ℃/min,热压压力为25 MPa,保压时间为40 min。整个热压过程保证炉内氩气压力0.1 MPa。由于石墨的还原作用,最终将与石墨粉末接触的部分Cu2O基体还原,形成Cu相作为导通相。
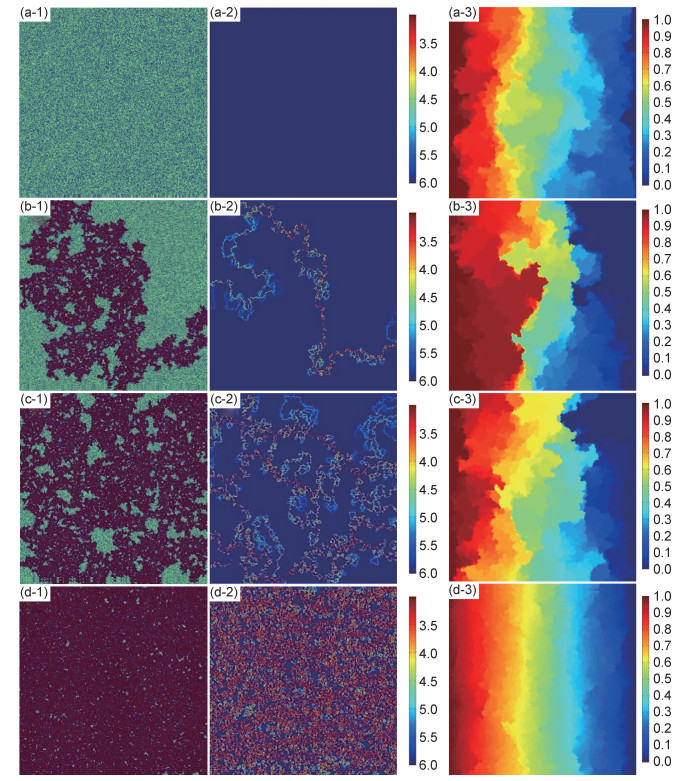
2 结果与分析图 2给出了二维正方晶格逾渗行为结果。图 2(a-1)~ (b-1)中红色部分代表形成了无限导通网络的导通相占比,绿色部分是非导通相占比。图 2(a-2)~(b-2)中蓝色部分代表未形成导通骨架部分,其他颜色为导通骨架通路部分,图 2(a-3)~(b-3)中从左至右为电压由高向低方向。可知,在导通相体积分数小于逾渗阈值1%时(图 2(a-1),(a-2), (a-3)),虽然在逾渗体系中没有形成无限网络以及导通骨架,但是由于在该体积分数下电压并非均匀分布,而是出现了波动,说明虽然没有形成整体无限导通网, 但是局部的导通网络已经形成。由于没有形成无限导通网络,通过体系的电流非常小。当导通相体积分数大于逾渗阈值1%时(图 2(b-2)),体系中出现了明显的无限导通网络结构,电压无序分布变得更为明显,开始出现有电流通过的骨架结构(图 2(b-1),(b-2), (b-3)), 在这个体积分数下体系无限导通网络中的骨架只有一支,属于临界导通状态。当导通相体积分数大于逾渗阈值1.1%时(图 2(c-1),(c-2),(c-3)),体系中无限导通网络体积分数明显增加。尽管导通相体积分数只增加了0.1%,但是,体系的电压分布变得更加无序,电流骨架由原来一支变成了两支, 说明增加的这部分导通相,使原先不属于无限导通网络的局部导通网络加入到无限导通网络结构中,因此形成的无限导通网络和骨架结构体积分数大量增加。当导通相体积分数大于逾渗阈值3%时(图 2(d-1),(b-2),(b-3)),可以明显看到体系中无限导通网络体积分数进一步增加,骨架结构已经基本布满整个体系(图 2(d-1),(d-2)),电压分布也开始向有序化变化(图 2(d-3)), 说明体系中的局部导通网络已经大部分成为无限导通网络,继续增加导通相体积分数已经不能使游离态的局部网络加入无限导通网络中,因此,添加的这部分导通相不能像在逾渗阈值处那样大量增加无限网络和骨架的体积分数,整个体系的导通相骨架变化已经趋于平缓。
|
图 2 二维晶格逾渗行为模拟结果 (a)导通相体积分数小于逾渗阈值体积分数1%;(b)导通相体积分数大于逾渗阈值体积分数1%;(c)导通相体积分数大于逾渗阈值体积分数1.1%;(d)导通相体积分数大于逾渗阈值体积分数3%;(1)导通相;(2)导通骨架;(3)电压分布 Fig. 2 Simulated percolation phenomenon of 2D square lattice (a)volume fraction is 1% lower than the percolation threshold; (b)volume fraction is 1% higher than the percolation threshold; (c)volume fraction is 1.1% higher than the percolation threshold; (d)volume fraction is 3% higher than the percolation threshold; (1)conducting phase; (2)conducting backbone; (3)voltage distribution |
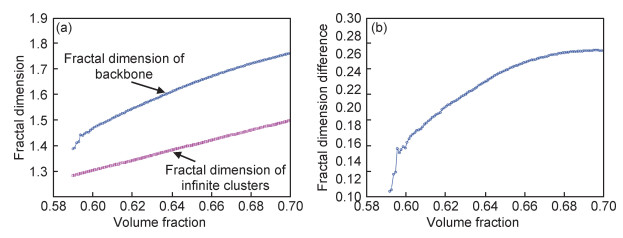
二维正方晶格逾渗体系由导通相与非导通相构成。其中,导通相由已经形成相互连接的“无限导通团簇”与没有相互连接的“岛状团簇”组成,而无限导通团簇由“导通骨架”和“死端”构成[16],因此导通相的体积分数要高于导通骨架的体积分数。图 3给出了二维正方晶格无限导通团簇与导通骨架的分形维数随导通相体积分数的变化曲线。由图 3(a)可以看出,导通骨架的分形维数要高于无限导通团簇的分形维数。但仅仅通过导通骨架分形维数高于无限导通团簇的分形维数,并不能说明导通骨架的复杂程度高于无限导通团簇的复杂程度。在这种情况下,需要通过对比无限导通团簇与导通骨架分形维数的差值来进行分析。如图 3(b)所示,无限导通团簇与导通骨架的差值并不是一个定值,而是在逾渗阈值附近较高,随着导通相体积分数的增加递减,趋于定值。在导通相体积分数很高时(高于逾渗阈值约10%),无限导通网络中骨架的密度很高,此时,骨架体积分数的增加和导通相增加的体积分数基本相同,因此,在这个阶段,体积含量增加对无限导通团簇和导通骨架分形维数之差的贡献基本为零。说明在逾渗阈值附近, 导通骨架分形维数高于无限导通团簇分形维数不仅仅是由导通相体积分数高于导通骨架体积分数造成的。另外,导通相的分形维数呈平滑上升趋势,而导通骨架的分形维数却在逾渗阈值附近出现明显的波动,说明在逾渗阈值附近导通骨架的分布和复杂程度出现波动,而对于整个体系来说,导通相的分布具有更好的统计性,不会出现分维波动。
|
图 3 二维正方晶格逾渗体系分形维数 (a)导通骨架与无限导通团簇的分形维数;(b)导通骨架与无限导通团簇的分形维数差值 Fig. 3 Fractal dimensions of 2D square lattice percolation system (a)fractal dimension of backbone and infinite clusters; (b)fractal dimension difference between backbone and infinite clusters |
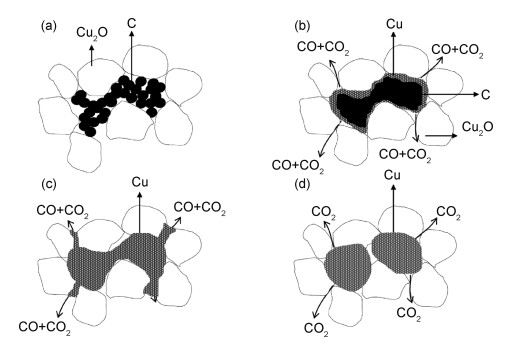
图 4给出了石墨热压还原制备Cu/Cu2O金属陶瓷过程示意图。大致可以分为4个阶段:(1)将石墨与Cu2O基体进行充分混合,使石墨粉体均匀填充于Cu2O陶瓷颗粒间隙中(图 4(a));(2)随着环境温度的升高,石墨开始与Cu2O基体发生还原反应,生成CO与CO2气体(图 4(b));(3)还原反应结束后,反应产物金属Cu将分布在原来的Cu2O陶瓷颗粒堆积孔隙处,以及由于CO气体流动,还原Cu2O陶瓷颗粒表面生成的金属Cu;(4)通过热压烧结,使得整体材料致密,金属Cu相最终均匀分布在Cu2O陶瓷基体中。
|
图 4 石墨热压还原制备Cu/Cu2O金属陶瓷过程示意图 (a)还原前;(b)还原中;(c)还原结束;(d)热压还原结束 Fig. 4 Schematic diagrams of the hot pressing graphite reduction process of Cu/Cu2O cermet (a)before reduction; (b)during reduction; (c)after reduction; (d)after hot-pressing reduction |
反应过程为:
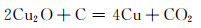
|
(2) |
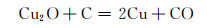
|
(3) |
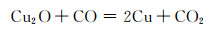
|
(4) |
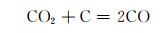
|
(5) |
式(2),(3)属于固相反应,式(4),(5)属于气相反应。
图 5是热压还原法制备得到的Cu/Cu2O金属陶瓷的金相显微组织以及对应的二值化处理图。分形维数是通过对二值化处理后的图片进行记盒维数的计算得到的。

|
图 5 热压还原法制备的Cu/Cu2O金属陶瓷显微组织(a)及对应的二值化处理图(b) Fig. 5 Microstructure(a) and corresponding binarized image(b) of C reduced hot-pressing Cu/Cu2O cermet |
在双相复合材料中,导通相的无限导通网络有两种结构,一种是骨架结构,另一种是死端结构。骨架结构代表能够为导通提供导通路径的实际路线,只包括环路和单连两种。死端结构是除了骨架之外的其他形式的结构。死端结构相对复杂,其形态各种各样,变化繁多。所以,随着导通相形态的变化,如果死端的增量大于骨架的增量,则分形维数将会出现下降。在这个体系中,分形维数下降,说明在形成逾渗导通之后再增加的那部分导通相体积中,增加到死端的体积是多于增加到骨架的体积的。随着进一步的导通相体积增加,多余的死端相互连接,骨架密度进一步增加,从而导致分形维数的上升。因此,在热压还原法制备的金属陶瓷中,由于热压压力的存在,导致复合材料导通相结构在平行热压压力方向与垂直热压压力方向存在差异,因此会导致微观结构出现区别。
图 6为平行热压方向与垂直热压方向的金属陶瓷记盒维数。图中曲线分为两个部分,第一部分(lgε < 3)是该截面导通相的分形维数,第二部分(lgε>3)的D=2.0是整个截面的分形维数。平行热压方向与垂直热压方向的导通相分形维数分别为D//=1.29和D⊥=1.37, 差值约为0.1。该分形维数差值可以给出具有非均匀分布第二相或有聚向性区别的复合材料第二相的微观结构差异。

|
图 6 不同热压方向的金属陶瓷记盒分形维数 (a)平行热压方向;(b)垂直热压方向 Fig. 6 Box-counting fractal dimension of cermet along with different hot-pressing directions (a)parallel to hot-pressing direction; (b)perpendicular to hot-pressing direction |
(1) 随着导通相Cu含量体积分数的增加,Cu/Cu2O金属陶瓷的分形维数呈现增加趋势。在相同导通相体积分数下,不同导通相的结构和分布导致不同的分形维数。
(2) 在逾渗体系中,无限网络总量和骨架总量随着导通相体积分数的增加而增加。但是,骨架密度在逾渗阈值附近并不随着导通相体积分数的增加而增加。
(3) 导通相的分形维数呈现平滑上升趋势,且整体高于导通骨架的分形维数。在逾渗阈值附近,导通骨架的分形维数出现波动。导通相分形维数和导通骨架分形维数的差值随体积分数的增加而减小,说明在逾渗阈值附近导通骨架的复杂程度小于导通相的复杂程度。
(4) 随着Cu相体积含量的增加,Cu/Cu2O金属陶瓷导通骨架密度的增量导致其分形维数继续保持增长。另外,平行热压方向与垂直热压方向的导通相分形维数相差约0.1。
| [1] |
CACCIA M, TABANDEH-KHORSHID M, ITSKOS G, et al. Ceramic-metal composites for heat exchangers in concentrated solar power plants[J]. Nature, 2018, 562(7727): 406-409. DOI:10.1038/s41586-018-0593-1 |
| [2] |
SANDHAGE K H, HENRY A S. Methods for manufacturing ceramic and ceramic composite components and components made thereby: US 2017/028091[P]. 2017-04-18.
|
| [3] |
JIN E Q, LI J, GENG K Y, et al. Designed synthesis of stable light-emitting two-dimensional sp2 carbon-conjugated covalent organic frameworks[J]. Nature Communications, 2018, 9(1): 4143. DOI:10.1038/s41467-018-06719-8 |
| [4] |
LEE S, KOO J, KANG S K, et al. Metal microparticle-polymer composites as printable, bio/ecoresorbable conductive inks[J]. Materials Today, 2018, 21(3): 207-215. DOI:10.1016/j.mattod.2017.12.005 |
| [5] |
DIERICKX S, MUNDLOCH T, WEBER A, et al. Advanced impedance model for double-layered solid oxide fuel cell cermet anodes[J]. Journal of Power Sources, 2019, 415: 69-82. DOI:10.1016/j.jpowsour.2019.01.043 |
| [6] |
CATALANO M, TAURINO A, ZHU J T, et al. Dy-and Tb-doped CeO2-Ni cermets for solid oxide fuel cell anodes: electrochemical fabrication, structural characterization, and electrocatalytic performance[J]. Journal of Solid State Electrochemistry, 2018, 22(12): 3761-3773. DOI:10.1007/s10008-018-4064-2 |
| [7] |
MEYER P, MASSOT L, GIBILARO M, et al. Electrochemical degradation mechanism of a cermet anode for aluminum production[J]. Materials Sciences and Applications, 2019, 10(9): 614-629. DOI:10.4236/msa.2019.109044 |
| [8] |
PAWLEK R P. Light metals 2016[M]. Cham: Springer, 2016: 1126-1133.
|
| [9] |
XIONG R, HU K S, GRANT A M, et al. Ultrarobust transparent cellulose nanocrystal-graphene membranes with high electrical conductivity[J]. Advanced Materials, 2016, 28(7): 1501-1509. DOI:10.1002/adma.201504438 |
| [10] |
XIONG W W, LIU H L, CHEN Y Z, et al. Highly conductive, air-stable silver nanowire@iongel composite films toward flexible transparent electrodes[J]. Advanced Materials, 2016, 28(33): 7167-7172. DOI:10.1002/adma.201600358 |
| [11] |
VIJAY S, WANG L T, LYPHOUT C, et al. Surface characteristics investigation of HVAF sprayed cermet coatings[J]. Applied Surface Science, 2019, 493: 956-962. DOI:10.1016/j.apsusc.2019.07.079 |
| [12] |
QIAN W, PANG X M, ZHOU J X, et al. High temperature spectral selective TiC-Ni/Mo cermet-based coatings for solar thermal systems by laser cladding[J]. Solar Energy, 2018, 171: 247-257. DOI:10.1016/j.solener.2018.06.074 |
| [13] |
FARINA I, GOODALL R, HERNÁNDEZ-NAVAE, et al. Design, microstructure and mechanical characterization of Ti6Al4V reinforcing elements for cement composites with fractal architecture[J]. Materials & Design, 2019, 172: 107758. |
| [14] |
YANG C, CUI X Y, ZHANG H X, et al. Fractal dendrite-based electrically conductive composites for laser-scribed flexible circuits[J]. Nature Communications, 2015, 6: 8150. DOI:10.1038/ncomms9150 |
| [15] |
ZHAO Y S, FENG Z C, LV Z X, et al. Percolation laws of a fractal fracture-pore double medium[J]. Fractals, 2016, 24(4): 1650053. DOI:10.1142/S0218348X16500535 |
| [16] |
XIE N, SHAO W Z, FENG L C, et al. Fractal analysis of disordered conductor-insulator composites with different conductor backbone structures near percolation threshold[J]. The Journal of Physical Chemistry C, 2012, 116(36): 19517-19525. DOI:10.1021/jp3040242 |
| [17] |
BAFEKRPOUR E. Advanced composite materials: properties and applications[M]. Berlin, Germany: De Gruyter, 2017: 440-467.
|
| [18] |
BADARD M, COMBESSIS A, ALLAIS A, et al. Modeling the dynamic percolation of carbon nanotubes and revisiting critical exponents[J]. Materials Chemistry and Physics, 2017, 191: 89-95. DOI:10.1016/j.matchemphys.2017.01.043 |
| [19] |
NAN C W. Physics of inhomogeneous inorganic materials[J]. Progress in Materials Science, 1993, 37(1): 1-116. DOI:10.1016/0079-6425(93)90004-5 |
| [20] |
WANG M Y, GURUNATHAN R, IMASATO K, et al. A percolation model for piezoresistivity in conductor-polymer composites[J]. Advanced Theory and Simulations, 2019, 2(2): 1800125. DOI:10.1002/adts.201800125 |
| [21] |
NISTAL A, GARCIA E, PÉREZ-COLL D, et al. Low percolation threshold in highly conducting graphene nanoplatelets/glass composite coatings[J]. Carbon, 2018, 139: 556-563. DOI:10.1016/j.carbon.2018.07.030 |
 2022, Vol. 50
2022, Vol. 50


