文章信息
- 支盛兴, 李兴刚, 袁家伟, 李永军, 马鸣龙, 石国梁, 张奎
- ZHI Sheng-xing, LI Xing-gang, YUAN Jia-wei, LI Yong-jun, MA Ming-long, SHI Guo-liang, ZHANG Kui
- 挤压态AZ40镁合金热变形行为及热加工图分析
- Analysis of hot deformation behavior and processing map of extruded AZ40 alloy
- 材料工程, 2021, 49(11): 136-146
- Journal of Materials Engineering, 2021, 49(11): 136-146.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2021.000136
-
文章历史
- 收稿日期: 2021-02-09
- 修订日期: 2021-04-06
2. 有研工程技术研究院有限公司, 北京 101407;
3. 北京有色金属研究总院, 北京 100088
2. GRIMAT Engineering Institute Co., Ltd., Beijing 101407, China;
3. General Research Institute for Nonferrous Metals, Beijing 100088, China
镁及其合金作为最轻的金属结构材料,密度仅为1.74 g/cm3,是钢的1/4,Al的2/3,具有比强度高、比刚度高、阻尼性能好等优点,被誉为“21世纪的绿色功能材料”,在航空航天、民用运输及电子产品等领域具有广阔的应用前景,但是由于镁合金的耐腐蚀性较差,限制了其进一步的应用[1-2]。随着常规油气资源的不断开发与耗竭,页岩石油气等非常规油气资源将成为未来能源的重要接替者。水平井分段压裂技术作为一种用于此类油气资源开采的主要方法,已在许多石油和天然气公司广泛使用[3-4]。其中,桥塞是分段压裂技术中不可或缺的封堵压裂工具。镁合金在可溶性桥塞中具有广阔的应用前景,主要由于其电极电位低且易于腐蚀。新一代可溶性桥塞胀管部分为可溶性橡胶材料制成,其余部分均为镁合金制成[5]。可溶性橡胶材料不仅溶解较慢,容易造成二次堵塞等问题,而且在桥塞胀管工作时容易发生回弹造成封堵失效。
为实现桥塞胀管工作时发生径向膨胀达到封堵目的,要求镁合金材料力学性能的各向异性较小,但采用常规挤压、锻压及轧制等变形工艺生产的镁合金材料易形成较强(0001)基面织构,导致力学性能具有很强的各向异性[6-9]。多向锻造由于其工艺流程简单,设备简便和加工成本低等诸多优点,在工业生产中应用广泛。与单向成形工艺相比,多向锻造能够实现织构弱化和特定滑移系的启动,使材料各向同性得到提高。Jamali等[10]对挤压态ZK60合金在200 ℃进行多向锻造后发现,经过8道次锻造后,材料的平均晶粒尺寸由12.7 μm细化至1.9 μm;同时,挤压后的基面织构偏转了45°;晶粒的细化和织构转化对材料塑性提高有着关键作用。Xia等[11]对Mg-Gd-Y-Nd-Zr合金进行多向锻造后发现,随着多向锻造道次增加,再结晶晶粒体积分数显著增加,3道次多向锻造后材料的平均晶粒尺寸从200 μm减小到5.4 μm,之后平均晶粒尺寸几乎不变,6次多向锻造后平均晶粒尺寸为5.1 μm;由于动态再结晶,动态析出和锻造力方向变化的共同作用,随着多向锻造道次的增加,基面织构逐渐减弱,经过6次多向锻造加工后,材料的塑性和铸态合金相比提高了15倍。Chen等[12]研究表明,AZ31B合金经多向锻造变形后,其晶粒无论是尺寸还是形状都是非常不规则的,织构被弱化。AZ40合金塑性较好,变形能力较强,在桥塞工作过程中能替代可溶性橡胶达到封堵作用,并且AZ40合金溶解速率适中,可以通过调整腐蚀介质调节溶解速率,是可溶性桥塞的良好候选材料;然而镁合金的加工窗口较窄,在多向锻造过程中,如果变形参数控制不当,合金容易造成材料开裂。所以许多学者对AZ40镁合金的热变形行为进行了研究,其中刘克威等[13]通过AZ40合金的热压缩实验优化Fields-Backofen模型,提高了预测精度。蔡志伟等[14]对均匀化AZ40M合金的热变形行为进行了研究,结果表明AZ40M合金的流变应力受加工硬化和再结晶软化共同影响,其热变形行为对温度及应变速率变化都很敏感。翟显伟等[15]对均匀化AZ40镁合金的研究也表明了这一点。但是目前对于一次变形后的AZ40镁合金特别是挤压态AZ40镁合金的热变形行为的研究较少。为了更好地指导后续的多向锻造过程,本工作对挤压态AZ40镁合金进行不同条件的热变形行为进行了研究,在此基础上得到了挤压态AZ40合金本构方程并绘制了热加工图,为制定合理的锻造工艺提供了依据。
1 实验原料及方法研究采用的原始材料为挤压态AZ40镁合金,合金尺寸为ϕ160 mm×320 mm,挤压比为17 ∶1,挤压速度为0.1 mm/s,合金的名义成分见表 1。
| Al | Zn | Mn | Mg |
| 4 | 0.75 | 0.5 | Bal |
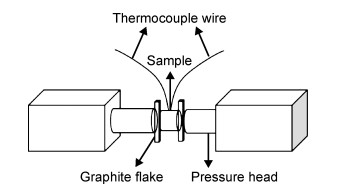
在Gleeble-3500热测试机上进行单向热压实验。将石墨垫片放置在两侧,以防止压头和样品之间在压缩过程中发生摩擦引起变形出现鼓状,并将电偶丝焊接在样品圆柱面的中心位置,以5 ℃/s进行升温,达到目标温度保温5 min后进行恒温恒应变速率压缩,实验装置如图 1所示,变形温度为543,573,603 K和633 K,应变速率为0.001,0.01,0.1 s-1和1 s-1,变形量为60%。完成压缩后立即淬火,以保留变形组织。沿轴向切割压缩试样,分别用240,600,1000,2000,5000目砂纸打磨切割面并进行机械抛光,然后用混合溶液进行腐蚀,混合液成分为2.5 mL乙醇+0.5 mL醋酸+1 mL蒸馏水+ 0.15 g苦味酸。使用Axiovert 200MAT光学显微镜对腐蚀后的合金金相进行观察。EBSD样品经打磨后进行电解抛光,观察合金样品使用Pegasus XM2扫描电子显微镜,获得试样合金织构信息,扫描电压为20 kV,扫描步长为0.8 μm,电解液选用硝酸乙醇混合溶液,混合液成分为80 mL乙醇+20 mL硝酸,抛光温度为-10 ℃,电解抛光5~50 s。
|
图 1 热压缩实验示意图 Fig. 1 Schematic diagram of hot compression test |
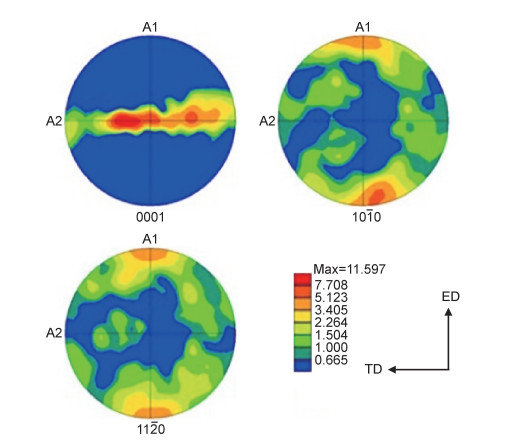
图 2为AZ40合金初始挤压态ED面的金相照片,可以看到,挤压态合金组织表现出较为明显的流线特征(图 2(a)),合金表现出了一定程度的混晶状态(图 2(b))。图 3为初始挤压态AZ40的极图,可以发现,初始挤压态合金主要为挤压基面织构,即{0001}基面平行于ED方向,且织构强度较大。

|
图 2 挤压态AZ40合金ED方向金相组织 (a)低倍;(b)高倍 Fig. 2 Microstructures of the extruded AZ40 alloy in extruded direction(ED) (a)low magnification; (b)high magnification |
|
图 3 挤压态AZ40合金极图 Fig. 3 Pole figures of the extruded AZ40 alloy |
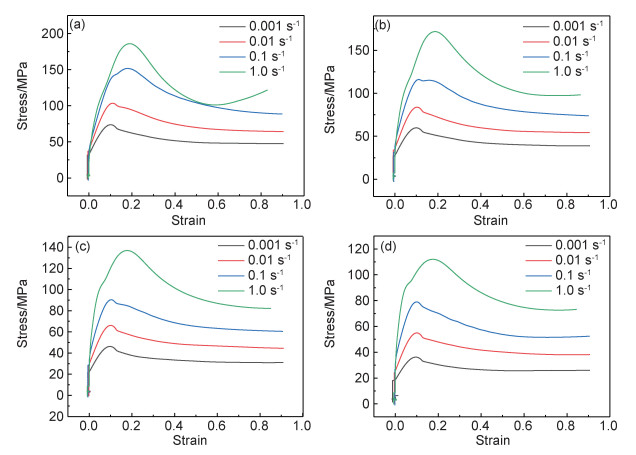
图 4为挤压态AZ40合金的热压缩真应力-真应变曲线。由图可知,合金的真应力-真应变曲线呈现出典型的动态再结晶特征,即在低应变阶段时,由于加工硬化的原因,材料的流变应力快速增加,随着变形的不断进行,动态再结晶的程度增加,并且合金的流变应力的上升速度由于动态再结晶的软化作用而减慢,直到达到峰值应力为止,合金到达峰值应力之后随着加工硬化作用的减弱,动态再结晶软化占据主导作用,合金流变应力逐渐减小,直到再结晶软化作用与加工硬化作用之间达到平衡,合金流变应力逐步稳定。当变形温度相同时,应变速率越高,合金再结晶时间越短,再结晶软化的效果越低,合金的峰值应力越高;当应变速率相同时,应变温度越高,再结晶软化的作用越明显,合金的峰值流变应力越小。
|
图 4 AZ40镁合金不同温度下真应力-真应变曲线 (a)543 K; (b)573 K; (c)603 K; (d)633 K Fig. 4 True stress-true strain curves of AZ40 alloy under different deformation temperatures (a)543 K; (b)573 K; (c)603 K; (d)633 K |
AZ40热压缩是一个热激活过程,可以用基于Arrhenius模型修正的Sellars等和Zener等[16-17]的双曲正弦函数,表示其应变温度、应变速率对流变应力的影响,见式(1)~(3)。式(1)包含变形温度和变形激活能,适用于所有的应力状况,而在低水平应力下,通常可用式(2)所表述的关系来描述;在高水平应力下,一般用式(3)描述所表述的关系。
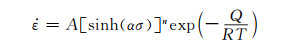
|
(1) |
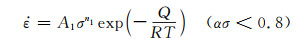
|
(2) |
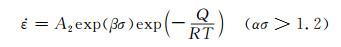
|
(3) |
式中:
分别对以上三式两边取对数后可得:

|
(4) |
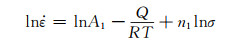
|
(5) |

|
(6) |
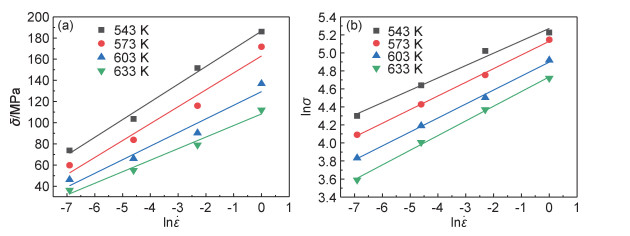
根据式(5)和式(6)可以得出,当变形温度T一定时,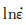
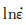
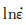
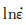
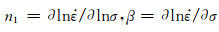
|
图 5 峰值应力与应变速率的关系
(a)σ-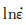 ;(b)lnσ- ;(b)lnσ-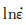 Fig. 5 Relationship between peak stress and strain rate
(a)σ-
Fig. 5 Relationship between peak stress and strain rate
(a)σ-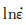 ; (b)lnσ- ; (b)lnσ-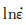
|
假设Q与温度无关,则可通过对式(4)两端进行偏微分来获得变形激活能:
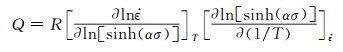
|
(7) |
式(4)和式(7)表明,当变形温度T确定时,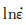
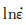

|
图 6 ln[sinh(ασ)]与应变速率及温度的关系
(a)ln[sinh(ασ)]-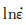 ;(b)ln[sinh(ασ)]-1/T; Fig. 6 Relationship between ln[sinh(ασ)]and strain rate, temperature
(a)ln[sinh(ασ)]- ;(b)ln[sinh(ασ)]-1/T; Fig. 6 Relationship between ln[sinh(ασ)]and strain rate, temperature
(a)ln[sinh(ασ)]-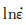 ; (b)ln[sinh(ασ)]-1/T; ; (b)ln[sinh(ασ)]-1/T;
|
本工作引入温度补偿系数Z参数来描述温度和变形速率之间的关系。此参数与温度T相关,与流变应力σ没有明显关系。Zener和Hollomon第一次提出Z参数[18-19],可表示为:
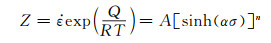
|
(8) |
对式(8)两端取对数可得:
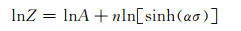
|
(9) |
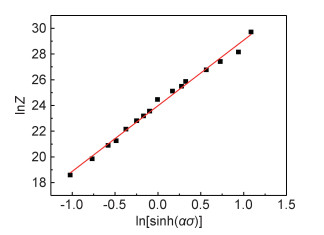
将变形激活能Q值代入式(8),进而获得Z值,根据式(9)可知lnZ与ln[sinh(ασ)]呈线性关系,对lnZ-ln[sinh(ασ)]曲线进行绘制,如图 7所示。根据式(9)和图(7)可得,n为斜率,lnA为截距,经计算得,n=5.10023,A=2.58361×1010。通过在式(1)中输入得到的参数获得AZ40镁合金热压缩本构方程如下:
|
图 7 lnZ-ln[sinh(ασ)]关系曲线图 Fig. 7 Relationship between lnZ and ln[sinh(ασ)] |
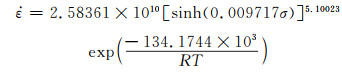
|
(10) |
式(10)中材料常数α,n,Q,A均为确定值,未考虑应变对流变应力的影响,为了对获得的本构模型进行验证,将材料常数α,n,Q,lnA分别对应变ε进行5阶多项式拟合,如式(11)所示。
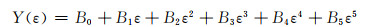
|
(11) |
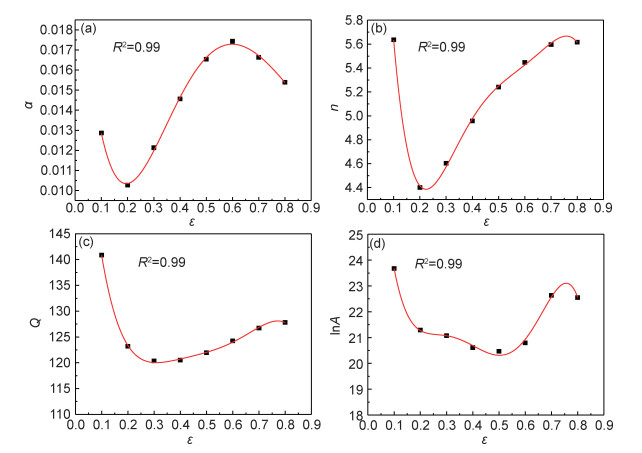
式中:Y(ε)分别为α,n,Q,lnA;ε为应变; B0~B5为多项式拟合系数,拟合结果和多项式系数如图 8和表 2所示。
|
图 8 材料常数与应变关系 (a)α;(b)n;(c)Q;(d)lnA Fig. 8 Relationship between material constants and strain (a)α; (b)n; (c)Q; (d)lnA |
| Constant | B0 | B1 | B2 | B3 | B4 | B5 |
| α | 0.0243 | -0.1808 | 0.7853 | -1.3426 | 1.0088 | -0.2829 |
| n | 10.466 | -77.314 | 357.69 | -750.27 | 749.32 | -289.02 |
| Q | 192.62 | -788.36 | 3320.1 | -6822.2 | 6907.7 | -2732.6 |
| lnA | 34.977 | -194.17 | 1051.4 | -2710.5 | 3267.5 | -1466.5 |
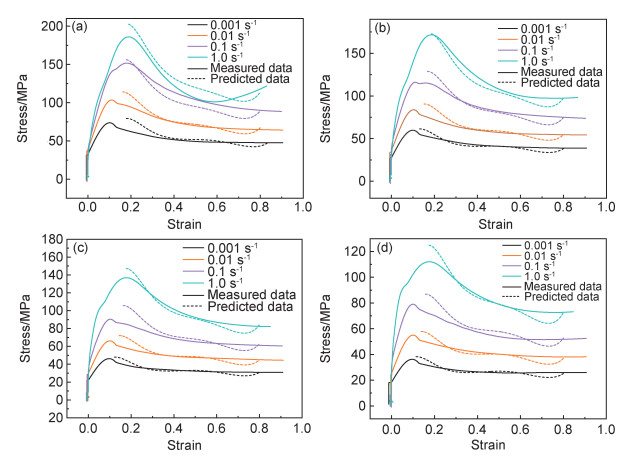
图 9为不同温度不同应变速率的实验真应力-真应变曲线和模型预测曲线对比,由图可得模型能够较好地预测合金在270~360 ℃和0.001~1.0 s-1范围内的流变应力,模型预测曲线与实验测试所得曲线吻合度较高。
|
图 9 不同温度和应变速率下流动应力预测值与实验结果的对比 (a)543 K; (b)573 K; (c)603 K; (d)633 K Fig. 9 Comparison between experimental and predicted flow stress with different temperatures and strains (a)543 K; (b)573 K; (c)603 K; (d)633 K |
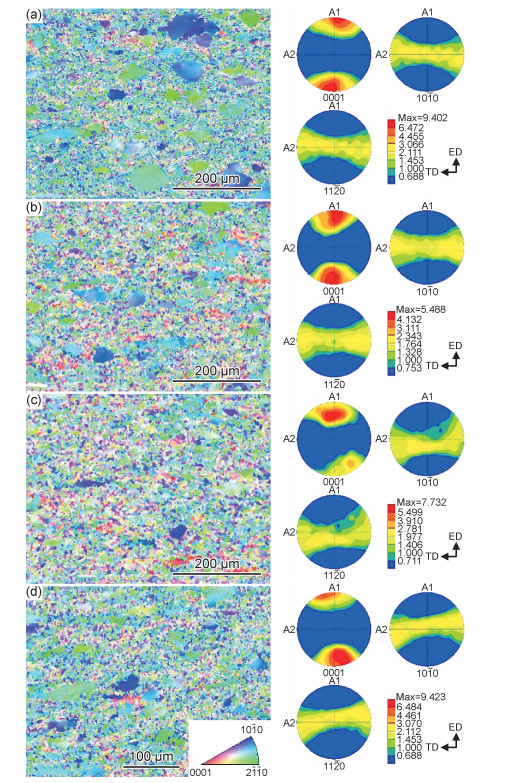
图 10为AZ40合金在不同条件下的EBSD组织观察图。由图可见,随着温度的升高和变形速率的降低,合金的再结晶程度逐渐提高。图中的晶粒颜色以绿色和蓝色为主,呈现了明显的取向性。在T=543 K,







|
图 10 AZ40合金不同变形条件下的EBSD组织观察
(a)T=543 K, =0.1 s-1;(b)T=573 K, =0.1 s-1;(b)T=573 K, =0.1 s-1;(c)T=603 K, =0.1 s-1;(c)T=603 K, =0.1 s-1;(d)T=573 K, =0.1 s-1;(d)T=573 K, =1.0 s-1
Fig. 10 EBSD images of the AZ40 alloy under different deformation conditions
(a)T=543 K, =1.0 s-1
Fig. 10 EBSD images of the AZ40 alloy under different deformation conditions
(a)T=543 K,  =0.1 s-1; (b)T=573 K, =0.1 s-1; (b)T=573 K,  =0.1 s-1; (c)T=603 K, =0.1 s-1; (c)T=603 K,  =0.1 s-1; (d)T=573 K, =0.1 s-1; (d)T=573 K,  =1.0 s-1 =1.0 s-1
|
|
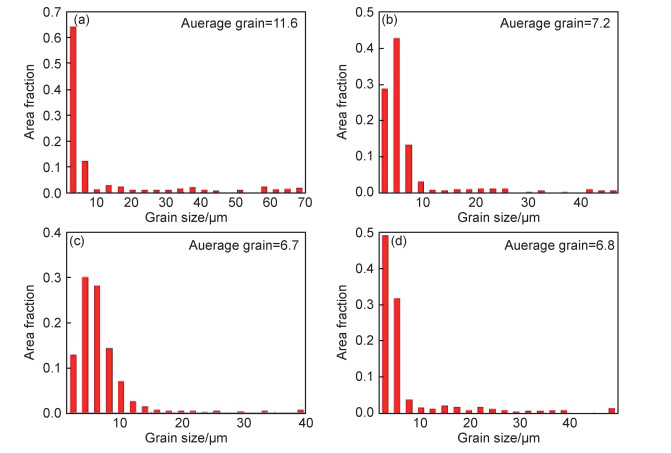
图 11 AZ40合金不同变形条件下的平均晶粒尺寸
(a)T=543 K, =0.1 s-1;(b)T=573 K, =0.1 s-1;(b)T=573 K, =0.1 s-1;(c)T=603 K, =0.1 s-1;(c)T=603 K, =0.1 s-1;(d)T=573 K, =0.1 s-1;(d)T=573 K, =1.0 s-1
Fig. 11 Average grain size of the AZ40 alloy under different deformation conditions
(a)T=543 K, =1.0 s-1
Fig. 11 Average grain size of the AZ40 alloy under different deformation conditions
(a)T=543 K,  =0.1 s-1; (b)T=573 K, =0.1 s-1; (b)T=573 K,  =0.1 s-1; (c)T=603 K, =0.1 s-1; (c)T=603 K,  =0.1 s-1; (d)T=573 K, =0.1 s-1; (d)T=573 K,  =1.0 s-1 =1.0 s-1
|
动态材料模型(DMM)是基于大塑性变形的连续介质力学、物理系统模拟和不可逆热动力学等方面的基本原理建立起来的[21]。该模型的基本原理为假设将热变形的加工件作为一个能量耗散体,在塑性加工过程中,将外界输入加工件的总能量P在以下两方面消耗:加工件发生塑性变形所消耗的能量,用耗散量G表示;加工件变形过程中组织变化而耗散的能量,用耗散协量J表示。
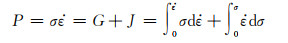
|
(12) |
这两种能量所占比例取决于加工件在一定应力下的应变速率敏感指数:
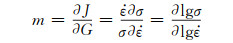
|
(13) |
在特定温度和变形下加工零件的应力和应变速率, 存在下面的本构关系:

|
(14) |
式中:K为材料常数,与应变速率无关,将式(14)代入式(12)中可得:
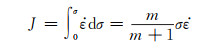
|
(15) |
假如材料是理想的线性耗散状态(m为1)时,J将达到此时的Jmax最大值,此时则有:

|
(16) |
在此引入反映材料功率分散特性的无量纲参数,即功率耗散性能η:
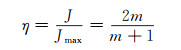
|
(17) |
η参数描述了待加工件对在给定温度和变形范围内工作的不同微观机制的基本反应,根据η的取值形成了功率耗散图,并依据变形速率和温度显示不同的区域。
根据大应力变塑性变形过程中的最大值原理,当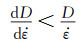
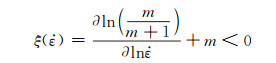
|
(18) |
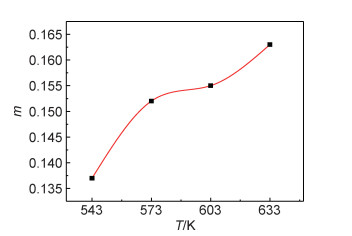
以动态材料模型(DMM)为基础,其条件是在一定应变和变形温度下,一般采用3次样条函数对lnσ与 

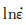
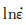
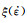
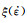





|
图 12 挤压态AZ40合金应变速率敏感指数m图 Fig. 12 Strain rate sensitivity exponent m of the extruded AZ40 alloy |

|
图 13 挤压态AZ40合金热加工图 Fig. 13 Processing map of the extruded AZ40 alloy |
(1) 基于Arrhenius模型得到挤压态AZ40合金的本构方程为: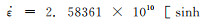
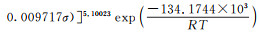
(2) 单向压缩后产生典型的压缩基面织构,通过对热压缩后金相组织及EBSD分析得到合金再结晶规律,即合金的再结晶程度随着温度的降低和应变速率的提高而降低;粗大的未再结晶晶粒有明显的〈1010〉‖ND和〈2110〉‖ND两种取向,而再结晶晶粒取向随机。
(3) 根据DMM理论,通过叠加功率耗散图和失稳图得到材料的热加工图,进而确定了该合金的失稳区,根据功率耗散因子大小初步确定了合金的3个可加工工艺:T=543 K,



| [1] |
DAI X J, YANG X, JING L, et al. Research progress in ultrafine grain magnesium alloy by equal channel angular pressing[J]. Chinese Journal of Rare Metals, 2020, 44(12): 96-103. |
| [2] |
LI X X, LIU Z, WANG Y, et al. Hot tearing defects of as-cast Mg-xZn-0.5Y-0.5Zr alloys[J]. Chinese Journal of Rare Metals, 2020, 44(7): 697-705. |
| [3] |
王林, 张世林, 平恩顺, 等. 可降解桥塞研制及其性能评价[J]. 科学技术与工程, 2017, 17(24): 228-232. WANG L, ZHANG S L, PING E S, et al. Development and performance evaluation of the degradable bridge plug[J]. Science Technology and Engineering, 2017, 17(24): 228-232. DOI:10.3969/j.issn.1671-1815.2017.24.039 |
| [4] |
刘辉, 喻冰, 杨海, 等. 可溶桥塞镶齿卡瓦研制及实验评价[J]. 钻采工程, 2018, 41(6): 76-78. LIU H, YU B, YANG H, et al. Development and experimental evaluation of insert slip for dissolvable bridge plug[J]. Drilling & Production Technology, 2018, 41(6): 76-78. |
| [5] |
刘统亮, 施建国, 冯定, 等. 水平井可溶桥塞分段压裂技术与发展趋势[J]. 石油机械, 2020, 48(10): 103-110. LIU T L, SHI J G, FENG D, et al. Technical status and development trend of staged fracturing with dissoluble bridge plug in horizontal well[J]. China Petroleum Machinery, 2020, 48(10): 103-110. |
| [6] |
陈振华. 镁合金[M]. 北京: 化学工业出版社, 2004. CHEN Z H. Magnesium alloy[M]. Beijing: Chemical Industry Press, 2004. |
| [7] |
YAMASHITA A, HORITA Z, LANGDON T G, et al. Improving the mechanical properties of magnesium alloy through severe plastic deformation[J]. Materials Science and Engineering: A, 2001, 300(1/2): 142-147. |
| [8] |
XU C, FURUKAWA M, HORITA Z. The evolution of homogeneity and grain refinement during equal-channel angular pressing: a model for grain refinement in ECAP[J]. Materials Science and Engineering: A, 2005, 398(1/2): 66-76. |
| [9] |
SEGAL V M, REZNIKOVVI, DROTYSHEVKIJAE A, et al. Plastic working of metals by simple shear[J]. Russian Metallugy, 1981, 1: 99-105. |
| [10] |
JAMALI A, MAHMUDI R. Evolution of microstructure, texture, and mechanical properties in a multi-directionally forged zk60 mg alloy[J]. Materials Science and Engineering: A, 2019, 752: 55-62. DOI:10.1016/j.msea.2019.02.095 |
| [11] |
XIA X S, CHEN Q, ZHAO Z D, et al. Microstructure, texture and mechanical properties of coarse-grained Mg-Gd-Y-Nd-Zr alloy processed by multidirectional forging[J]. Journal of Alloys and Compounds, 2015, 623: 62-68. DOI:10.1016/j.jallcom.2014.10.084 |
| [12] |
CHEN C, SONG L H, DU X H, et al. Enhanced mechanical property of AZ31B magnesium alloy processed by multi-directional forging method[J]. Materials Characterization, 2017, 131: 72-77. DOI:10.1016/j.matchar.2017.05.010 |
| [13] |
刘克威, 谭安平. AZ40M镁合金的Fields-Backofen模型及加工图[J]. 特种铸造及有色合金, 2020, 40(2): 143-147. LIU K W, TAN A P. Fields-Backofen model and processing map of AZ40M alloy[J]. Special Casting & Nonferrous Alloy, 2020, 40(2): 143-147. |
| [14] |
蔡志伟, 陈拂晓, 郭俊卿. AZ41M镁合金热变形行为及本构方程[J]. 材料热处理学报, 2015, 36(11): 65-71. CAI Z W, CHEN F X, GUO J Q. Hot deformation behavior and constitutive equation of AZ41M magnesium alloy[J]. Transactions of Materials and Heat Treatment, 2015, 36(11): 65-71. |
| [15] |
翟显伟, 秦聪祥. AZ41镁合金热变形动力学及其应变硬化行为的研究[J]. 热加工工艺, 2015, 36(10): 103-105. ZHAI X W, QIN C X. Study on hot deformation kinetics and strain hardening[J]. Hot Working Technology, 2015, 36(11): 65-71. |
| [16] |
SELLARS C M, MCTEGAR W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138. DOI:10.1016/0001-6160(66)90207-0 |
| [17] |
ZENER M, HOLLOMON J. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15: 22-23. DOI:10.1063/1.1707363 |
| [18] |
王家毅, 米振莉, 李辉, 等. 基于热加工图6082铝合金锻造工艺优化及强化机制研究[J]. 稀有金属, 2019, 43(2): 113-121. WANG J Y, MI Z L, LI H, et al. Isothermal forging process and strengthening mechanism of 6082 aluminum alloy through processing map[J]. Chinese Journal of Rare Metals, 2019, 43(2): 113-121. |
| [19] |
夏麒帆, 梁益龙, 杨春林, 等. TC4钛合金拉伸变形行为的研究[J]. 稀有金属, 2019, 43(7): 765-773. XIA Q F, LIANG Y L, YANG C L, et al. Tensile deformation behavior of TC4 titanium alloy[J]. Chinese Journal of Rare Metals, 2019, 43(7): 765-773. |
| [20] |
MA Q, LI B, WHITTINGTON W R, et al. Texture evolution during dynamic recrystallization in a magnesium alloy at 450℃[J]. Acta Materialia, 2014, 67: 102-115. |
| [21] |
PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of dynamic material behavior in hot deformation: forging of Ti-6242[J]. Metall Trans A, 1984, 15(10): 1883-1892. |
 2021, Vol. 49
2021, Vol. 49


