文章信息
- 唐闻远, 许英杰, 孙勇毅, 张卫红, 惠新育
- TANG Wen-yuan, XU Ying-jie, SUN Yong-yi, ZHANG Wei-hong, HUI Xin-yu
- 基于温度曲线优化的复合材料热压罐固化时间与固化质量协同控制
- Simultaneous control of curing time and curing quality of auto-clave processed composite based on optimization of temperature profile
- 材料工程, 2021, 49(9): 142-150
- Journal of Materials Engineering, 2021, 49(9): 142-150.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000716
-
文章历史
- 收稿日期: 2020-08-05
- 修订日期: 2021-02-07
热压罐成型工艺是纤维增强树脂基复合材料构件广泛使用的成型技术,尤其适用于大尺寸复合材料构件的成型。由于成型过程中热压罐内需要保持长时间的高温与高压条件,相对于非热压罐工艺,热压罐成型通常会导致较高的电力能源消耗。显然,减少热压罐成型时间可以有效降低能源消耗,但是如果缺乏合理的工艺设计,成型时间的缩短会直接造成固化不充分等缺陷,从而降低复合材料构件的固化质量。温度曲线是复合材料热压罐成型的重要工艺参数,一个完整的固化温度曲线包括升温速率、恒温温度、恒温时间、降温速率等参数,对温度曲线进行合理的优化设计,可以实现对成型时间与固化质量(固化程度、固化均匀性、固化变形)的协同控制。
近年来基于工艺优化的热压罐成型过程控制得到了广泛研究,特别是随着复合材料固化成型数值模拟方法[1-5]的日益完善,基于数值模拟结果对工艺参数进行优选或结合优化算法对工艺参数进行优化设计[6-10],为复合材料热压罐成型控制提供了重要参考。现有研究工作大多针对复合材料构件成型后的残余应力[6]、固化变形[7]、成型过程中的温度均匀性[8]、固化度均匀性[9-10]、温度峰值[11]等开展工艺优化,如何在控制质量的前提下缩短成型周期仍然存在很多问题,所以考虑对成型时间与固化质量的协同控制优化成为目前国内外学者的研究重点。
本工作基于复合材料热压罐固化成型的模拟计算方法,针对复合材料C形构件开展了固化成型的数值仿真,固化变形预测结果与实验测试结果吻合较好,验证了计算方法的合理性;在此基础上,以温度曲线的关键参数为设计变量,考虑成型时间与固化质量的协同控制需求,以热压罐成型时间最小化为目标,C形构件固化程度、固化均匀性、固化变形为约束,开展了温度曲线优化设计研究,并进一步开展了优化结果的实验验证。
1 固化成型数值模拟方法复合材料构件的固化成型过程中,预浸料树脂发生固化反应放热,导致复合材料内部形成复杂的温度梯度[12],温度和固化度互相耦合,引起非均匀固化,产生内应力;此外,成型过程中树脂基体会发生固化收缩[13],也会导致内应力的产生。本工作主要考虑固化成型过程中复合材料构件的固化程度、固化均匀性,以及内应力导致的构件固化变形,建立复合材料固化成型的数值模拟方法。
1.1 固化反应动力学模型树脂的固化反应动力学模型表征了固化过程中反应速率、温度以及固化度之间的关系。固化反应动力学模型按照构造机理可以分为微观模型[14]和唯象模型[15-16],由于唯象模型形式简单、易于通过实验拟合获得模型参数,被广泛应用于树脂的固化反应动力学建模。本工作采用文献[16]中的唯象模型如下:
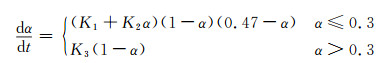
|
(1) |
式中:dα/dt表示固化速率;α表示固化度;t表示时间;Ki为固化反应速率常数并采用Arrhenius方程表示:

|
(2) |
式中:Ai为模型的频率因子;ΔEi为模型的活化能;T表示温度;R为理想气体常数。
1.2 热-化学耦合传热模型固化成型过程中,固化温度曲线、预浸料和模具的热传导以及树脂固化反应释放的热量,共同决定了复合材料构件的温度,固化反应放热可以视作内热源,且与固化反应相互耦合,构造热-化学耦合传热模型如下[17]:
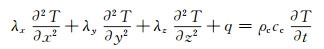
|
(3) |
式中:λx,λy和λz分别表示复合材料x,y和z方向的导热系数; ρc,cc分别表示复合材料的密度和比热容; q为热生成率,其表达式为:
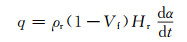
|
(4) |
式中:ρr为树脂密度;Vf为纤维体积分数;Hr为单位质量树脂固化反应释放的总热量,其数值可通过实验测得,固化速率dα/dt可通过式(1)求得。
1.3 树脂固化收缩固化反应过程中,树脂由黏流态逐渐固化并伴随有化学收缩,导致内应力的产生,这部分内应力与构件非均匀温度所形成的内应力共同作用,导致固化变形的产生。树脂的凝胶点是固化反应到达一定程度的标准,当树脂固化度到达凝胶点后,树脂的黏度会突然的变大,表现为一种不溶不熔的凝胶状态。通常可以采用黏度传感器对黏度变化进行观察计算以得到凝胶点。树脂在达到凝胶点之前,由于黏度较低,树脂流动明显从而抵消固化收缩导致的内应力。树脂达到凝胶点后,树脂流动困难无法抵消固化收缩导致的内应力。环氧树脂体系凝胶点一般在0.4左右,本工作取其值为0.38。
因此,本工作主要考虑凝胶点之后的树脂固化收缩,假设只有在凝胶点之后产生的固化收缩才对固化变形有影响。通常可采用热机械分析仪测量固化过程中的树脂固化收缩率[12]。仿真计算过程中,将固化收缩应变叠加到复合材料的应力应变计算中,即可耦合固化收缩的影响。
1.4 基于有限元方法的固化成型模拟本工作基于商业化有限元软件ABAQUS,建立了固化成型模拟计算方法。通过编写ABAQUS用户子程序,将固化动力学模型以及热-化学模型引入复合材料构件温度场与固化度场的计算,模拟复合材料的热-化学耦合传热过程;并定义复合材料的化学反应收缩应变,考虑树脂化学收缩对复合材料整体固化变形的影响。
计算流程如下:首先通过热-化学耦合传热分析来模拟复合材料的传热过程,计算得到单元每一节点在固化过程中的温度和固化度值;其次,将计算得到的各节点温度值和固化度值作为已知条件,考虑化学反应收缩应变,计算得到复合材料构件的内应力及后续的固化变形。
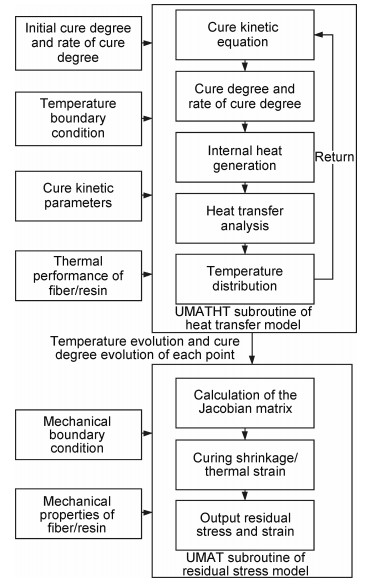
具体实现过程如下:通过USDFLD定义初始固化度及固化速率的场变量,并通过建立在UMATHT中的固化动力学方程计算当前固化度以及固化速率;在DISP以及FILM中添加有限元模型的温度边界条件;最后在Heat Transfer分析步中对以上子程序调用进行模型温度场的计算;将得到的温度与固化度等结果代入UMAT程序中,计算Jacobian矩阵,并结合UEXPAN定义的预浸料在固化过程中热胀冷缩以及树脂的化学收缩的热应变量,最终计算得到应力、应变。如图 1所示。
|
图 1 固化成型模拟方法流程图 Fig. 1 Workflow of cure simulation |
文献[18]给出了热压罐成型T800/M21 C形复合材料构件的固化变形测量结果,本工作针对上述C形构件,开展了固化成型后固化变形的模拟计算,并与测量结果进行了对比验证。
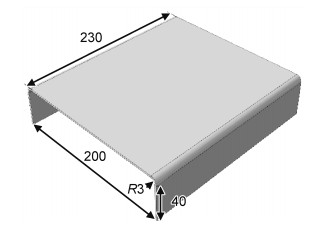
C形构件结构如图 2所示,先后采用三种铺层顺序成型,分别为[0/90]4s,[45/-45]4s和[0/45/-45/90]2s。预浸料单层厚度为0.125 mm,具体的性能参数[18]如表 1所示。本工作此处对复合材料固化过程中的力学性能进行了假设和简化,实际固化过程中,复合材料的性能具有时变演化特性,如何有效描述固化过程中材料的性能变化是固化仿真领域研究的难点。由于本工作的研究主要侧重于工艺优化模型与方法的建立和应用,尚未兼顾复合材料固化仿真模型的细化完善,因此忽略了复合材料的时变演化性能,假定材料性能为弹性且固化过程中不变。
|
图 2 C形构件几何模型 Fig. 2 Geometrical model of C-shaped part |
| Parameter | Value |
| E1/GPa | 157 |
| (E2=E3)/GPa | 8.5 |
| (G12=G23)/GPa | 4.5 |
| v12=v23 | 0.35 |
| ρ/(kg·m-3) | 1578 |
| c/(J·kg-1·K-1) | 862 |
| λ1/(W·m-1·K-1) | 5.43 |
| (λ2=λ3)/(W·m-1·K-1) | 0.4135 |
| β1/K-1 | -9×10-8 |
| β2=β3/K-1 | 3×10-5 |
| αC1 | 0 |
| αC2=αC3 | -1×10-2 |
| Note: E1, E2, E3—elastic modulus; G12, G23—shear modulus; ρ—density of composite; c—specific heat composite; λ1, λ2, λ3—heat conduction coefficient; β1, β2, β3—thermal expansion coefficient; αC1, αC2, αC3—chemical shrinkage coefficient | |
采用式(1)所示的固化反应动力学模型来描述树脂的固化速率,模型中各参数值[18]如表 2所示。
| Parameter | Value |
| A1/min-1 | 2.101×109 |
| A2/min-1 | -2.014×109 |
| A3/min-1 | 1.96×105 |
| ΔE1/(J·mol-1) | 8.07×104 |
| ΔE2/(J·mol-1) | 7.78×104 |
| ΔE3/(J·mol-1) | 5.66×104 |
| Hr/(J·kg-1) | 4.736×105 |
| R/(J·K-1·mol-1) | 8.3143 |
| Note: A1, A2, A3—frequency factors; ΔE1, ΔE2, ΔE3—activation energy; Hr—total heat of the curing of unit mass; R—perfect gas constant | |
固化工艺参数如下:初始温度为297 K,以2 K/min的升温速率升温到453 K,保温2 h,然后以2 K/min的降温速率降温至297 K,固化过程压力保持为0.6 MPa。
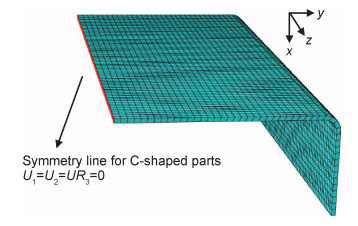
在成型过程中,由于复合材料与模具热变形的不匹配,会导致复合材料构件与模具之间产生相互作用,从而对构件的固化变形产生影响。本工作在成型C形构件时,在模具和复合材料之间使用了脱模剂,可以弱化模具-构件之间的相互作用,从而降低了模具的影响;此外,本工作中的C形构件尺寸较小,模具作用引起的固化变形非常小,因此,本工作在模拟固化变形时忽略了模具的影响。根据C形构件的几何尺寸与材料参数,在ABAQUS中构造了C形构件的有限元模型,单元类型为C3D8,单元尺寸为3 mm。模拟施加的边界条件如下:C形复合材料构件受到模具、辅助封装材料及罐内压力的作用,构件下表面直接与模具接触,施加沿模具型面法线方向的位移约束和三个方向上的旋转约束;构件上表面及侧面在辅助材料的封装下,处于罐内压力中,由于多余的树脂材料在成型过程中会在侧面被排出,因此仅在构件上表面施加压力场作用,以此来模拟构件在脱模前的约束状态。在脱模后,为防止有限元模型产生刚体位移,对缘条一侧的自由度进行约束,使构件在该状态下进行应力释放,如图 3所示,计算得到C形构件的固化变形。其中,仿真过程中的1,2,3方向分别对应坐标系的x,y,z 3个方向, U1是x方向轴向位移,U2是y方向轴向位移,UR3是z方向旋转。
|
图 3 C形构件有限元模型 Fig. 3 Finite element model of C-shaped part |
此外,固化过程中对构件下表面、上表面与侧面分布施加温度边界条件。构件下表面直接与模具接触,故在构件下表面施加与模具温度相等的温度场边界条件;构件上表面、侧面被辅助材料封装,与热空气进行对流换热,本工作设置构件上表面、侧面的对流换热系数为20 W·m-2·K-1[7]。
通过热-化学耦合分析计算得到模型中各个节点在固化过程中的温度和固化度值,然后将该温度值和固化度值作为已知条件,考虑化学反应收缩应变,计算得到复合材料构件的内应力与固化变形。
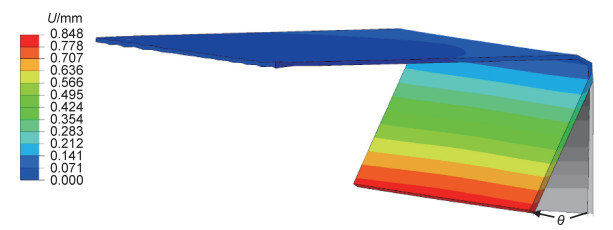
图 4给出了C形构件的固化变形模拟结果,可以看到变形方式主要为回弹变形,本工作以回弹角度θ表示。计算得到的不同铺层顺序C形构件的回弹角度与文献中测量结果[17]吻合较好,如表 3所示,验证了计算模型的合理性。
|
图 4 C形构件固化变形模拟结果 Fig. 4 Curing deformation simulation result of C-shaped part |
| Lay-up | Experimental spring-back angle/(°) | Numerical spring-back angle/(°) | Error/% |
| [0/90]4s | 1.34 | 1.358 | 1.34 |
| [0/45/-45/90]2s | 1.36 | 1.366 | 0.44 |
| [45/-45]4s | 1.48 | 1.370 | -7.43 |
本工作考虑热压罐成型复合材料C形构件成型时间与固化质量(固化程度、固化均匀性、固化变形)的协同控制,开展热压罐固化温度工艺曲线优化设计。
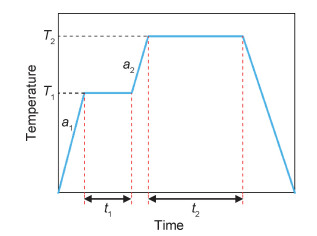
以温度工艺曲线作为优化参数,将温度曲线简化为如图 5的6个参数。其中,α1为第一段升温速率, K/min;α2为第二段升温速率, K/min;t1为第一平台保温时间, s;t2为第二平台保温时间, s;T1为第一平台保温温度, K;T2为第二平台保温温度, K;各参数取值范围如表 4所示。
|
图 5 温度曲线 Fig. 5 Temperature profile |
| Parameter | Range |
| α1/(K·min-1) | [0.5, 5.0] |
| α2/(K·min-1) | [0.5, 5.0] |
| T1/K | [388, 428] |
| T2/K | [448, 488] |
| t1/s | [0, 6000] |
| t2/s | [0, 9000] |
本工作分别开展两组优化设计,优化数学模型如下:
(1) 成型时间与固化程度、固化均匀性的协同控制优化
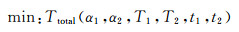
|
(5) |
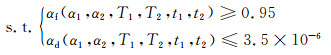
|
(6) |
(2) 成型时间与固化程度、固化变形的协同控制优化
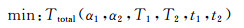
|
(7) |
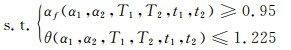
|
(8) |
式中:Ttotal为成型时间;αf为最终固化度;θ为固化变形回弹角;αd为固化度差值。本工作中固化度差值为成型过程各时刻下构件固化度最大值与最小值差值的集合取最大值,用以衡量固化的均匀性。
上述两类优化模型分别适用于工程应用中不同类型的复合材料构件:壁厚较厚的零件,固化过程中固化不均的问题更加突出,因此适合开展成型时间与固化程度、固化均匀性协同控制优化,同时,由于固化不均也是导致变形的一个重要因素,所以在减少固化度差值的同时,也可以减少固化变形;壁厚较薄的零件,固化变形的问题更加突出,因此适合开展成型时间与固化程度、固化变形协同控制优化。针对工程中同时包含薄壁与厚壁部分的较为复杂的零件,可视为同时考虑成型时间与固化程度、固化均匀性、固化变形的协同控制优化,需要在优化模型中同时选择固化程度、固化均匀性、固化变形为约束函数。
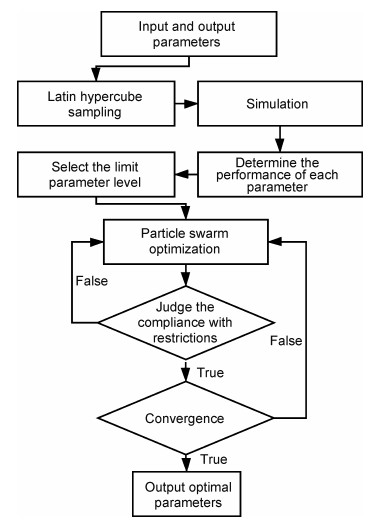
为了提高优化设计的效率,本工作采用了DOE(design of experiments)[19]与粒子群算法[20]集成的优化策略,如图 6所示。首先利用拉丁超立方抽样方法在参数范围内对工艺参数取样,进行固化成型仿真计算;然后通过DOE确定成型时间与固化质量接近最优值时的工艺参数水平,并对工艺参数范围进行重新界定;以DOE所得最优点作为粒子群算法起始组粒子点,在此基础上进行粒子群算法优化设计。
|
图 6 集成优化策略 Fig. 6 Integrated optimization strategy |
集成优化策略的优势包括:首先,超立方抽样可使样本点更均匀地分布在设计空间中,具有较好的全局性、均衡性与空间填充性;其次,DOE可确定各参数在理想条件时下水平,并确定协同控制参数的限制水平,对工艺参数的取值范围进行重新界定,增快收敛速度;最后,起始组粒子群中由于存在较为靠近全局最优解的粒子点,将加速对最优点的搜索,故集成优化策略可以快速寻找到全局最优解。
3.2 优化粒子群算法粒子群算法的速度更新、位置更新公式[21]为:
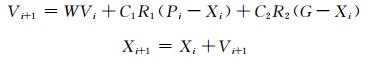
|
(9) |
式中:W为惯性因子;Vi为第i步速度;C1为单粒子速度更新常数,即粒子向自己历史最优解处移动的能力,称为认知参数;C2为全局速度更新常数,即粒子向当前全局最优解处移动的能力,称为环境参数;R1,R2为两个0到1之间的随机数;Pi为单个粒子点目前最优位置;G为全局粒子点最优位置。优化过程中还需设置Vmax值,当更新速度大于最大速度时,更新速度调整为最大速度。
惯性因子过大时,会造成粒子受较好结果的影响降低,不利于收敛,过小则会限制粒子扩展搜索空间的趋势,降低搜索新区域的能力,最终收敛于局部解。认知参数与环境参数的改变可以调整环境与粒子、粒子与粒子对收敛的影响,因集成优化策略在第一组粒子中就存在较为接近全局最优解的粒子,故在优化过程中稍放大这两个参数。过大的速度最大值会造成优化过程中,粒子群在最优解周围震荡,过小的速度会限制优化算法的搜索能力,增加计算成本。综合以上分析,本工作选取的参数值为:W=1,C1=2.2,C2=2.2,Vmax=1。
利用拉丁超立方抽样在取值范围内抽取50个粒子点,进行固化成型仿真计算,建立DOE空间,将DOE最优点输入粒子群算法,进行群组粒子数为20的粒子群算法优化,当参数超过80步没有波动判定为收敛。
3.3 优化结果与分析(1) 成型时间与固化程度、固化均匀性协同控制优化
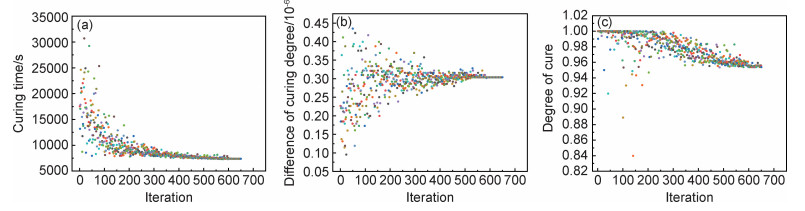
优化过程中固化时间、固化度最大差值以及最终固化度的迭代曲线(算例1)如图 7所示。
|
图 7 算例1各参数的迭代曲线(a)固化时间; (b)固化度差值; (c)固化度 Fig. 7 Iteration of parameters for case 1 (a)curing time; (b)difference of curing degree; (c)degree of cure |
表 5列出了初始工艺参数和优化后工艺参数的对比,可以看到,相比初始工艺参数,优化后的第一段升温速率与第二段升温速率均显著增大,第一平台保温温度和第二平台保温温度均升高,第一平台保温时间与第二平台保温时间则大幅减少。通过成型时间与固化程度、固化均匀性的协同控制优化,在满足固化程度与固化均匀性要求的前提下,成型时间降至7300 s,相比初始成型时间缩短了64%。此外,表 5给出了优化前后构件内的最大温差dT(成型过程中构件的最高温度和最低温度点的温差)。可以看到,优化后的温度曲线提高了升温速率和保温温度,虽然会一定程度增加构件的最高温度和最低温度点的温差,但由于本工作考虑的C形构件尺寸较小、壁厚较薄,构件具有较好的温度均匀性,零件内部与表面的温差较小,因此,与低升温速率条件下的最大温差dT相比差别很小。
| Parameter | Initial value | Optimized value |
| α1/(K·min-1) | 2.5 | 4.67046 |
| α2/(K·min-1) | 2.5 | 4.60595 |
| T1/K | 389 | 418 |
| T2/K | 450 | 468.95008 |
| t1/s | 3600 | 1111 |
| t2/s | 3600 | 600 |
| αf | 0.98 | 0.95386 |
| Ttotal/s | 20052 | 7300 |
| αd | 5.43773×10-3 | 3.03984×10-6 |
| dT/K | 3.6 | 4.5 |
(2) 成型时间与固化程度、固化变形协同控制优化
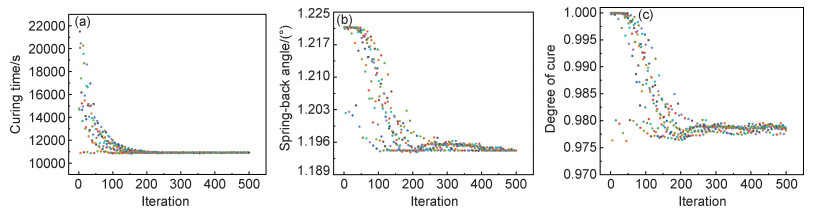
优化过程中固化时间、固化变形以及最终固化度的迭代曲线(算例2)如图 8所示。
|
图 8 算例2各参数的迭代曲线(a)固化时间; (b)固化变形; (c)固化度 Fig. 8 Iteration of parameters for case 2 (a)curing time; (b)curing deformation; (c)degree of cure |
表 6列出了初始工艺参数和优化后工艺参数的对比,可以看到,相比初始工艺参数,优化后的第一段升温速率与第二段升温速率略有增大,第一平台保温温度和第二平台保温温度均略有升高,第一平台保温时间与第二平台保温时间则大幅减少。通过成型时间与固化程度、固化变形的协同控制优化,在满足固化程度与固化变形要求的前提下,成型时间降至11000 s,相比初始成型时间缩短了45%。与上一组优化结果类似,优化后的温度曲线提高升温速率和保温温度,虽然会一定程度增加构件的最高温度和最低温度点的温差,但由于本工作考虑的C形构件尺寸较小、壁厚较薄,构件具有较好的温度均匀性,零件内部与表面的温差较小,如表 6所示,最大温差较低升温速率条件下的差别很小。
| Parameter | Initial value | Optimized value |
| α1/(K·min-1) | 2.5 | 3.17381 |
| α2/(K·min-1) | 2.5 | 2.60717 |
| T1/K | 389 | 399.50162 |
| T2/K | 450 | 452.73763 |
| t1/s | 3600 | 2686.39912 |
| t2/s | 3600 | 1952.44893 |
| αf | 0.98 | 0.97819 |
| Ttotal/s | 20052 | 11000 |
| θ/(°) | 1.225 | 1.194 |
| dT/K | 3.6 | 4.3 |
本工作进一步开展了优化结果的实验验证,考虑优化算例一中的固化均匀性指标目前实验过程中难以有效测试,本工作针对优化算例二开展了实验验证。实验验证思路如下:采用表 6中优化前与优化后的温度工艺曲线参数,分别进行T800/M21 C形复合材料构件的热压罐成型,构件几何尺寸与铺层参数与优化算例中一致,成型后对构件的固化变形进行测量。
热压罐成型中使用的预浸料铺层和钢模具如图 9所示,每种温度工艺曲线下各成型两件C形构件,对成型后构件的固化变形回弹角取平均值。

|
图 9 预浸料铺层和模具 Fig. 9 Prepreg laminates and mold |
成型得到的C形构件如图 10所示。采用游标万能角度尺对成型后的C形构件进行回弹角度测量,如图 11所示。优化前工艺成型构件的固化变形回弹角度平均值为1.21,优化后工艺成型构件的固化变形回弹角度平均值为1.18,可以看到,两种工艺曲线下得到的构件外形尺寸基本一致,符合固化变形要求,然而,优化后工艺曲线的成型时间相比优化前缩短了45%,显著提高了成型效率。

|
图 10 不同温度曲线成型的C形构件 Fig. 10 C-shaped part processed by different temperature profiles |

|
图 11 回弹角度测量 Fig. 11 Measure of the spring-back angle |
(1) 本工作面向热压罐成型复合材料构件的成本与质量要求,提出了基于温度曲线优化的固化时间与固化质量协同控制方法。针对T800/M21复合材料C形构件,首先开展了固化成型模拟计算与验证;在此基础上,发展了DOE与粒子群算法集成的优化策略,以C形构件固化温度曲线为设计变量,分别开展了成型时间与固化程度、固化均匀性的协同控制优化,以及成型时间与固化程度、固化变形的协同控制优化。
(2) 优化结果显示,通过温度曲线优化设计,在满足固化程度与固化均匀性要求的前提下,成型时间降至7300 s,相比初始成型时间缩短了64%,在满足固化程度与固化变形要求的前提下,成型时间降至11000 s,相比初始成型时间缩短了45%。
(3) 针对优化算例2开展了实验验证,优化前后两种工艺曲线下得到的构件外形尺寸基本一致,符合固化变形要求,然而,优化后工艺曲线的成型时间相比优化前缩短了45%,显著提高了成型效率。
(4) 未来工作中,本研究提出的优化模型和方法将进一步扩充,继续建立同时考虑成型时间与固化程度、固化均匀性、固化变形的协同控制优化模型,与其他优化方案进行对比,从而完善优化模型与方法。此外,本工作在计算C形构件温度场时并未考虑热压罐流场作用。合理考虑热压罐流场作用对提高热压罐固化成型仿真精度具有重要意义,考虑到本工作所选C形构件尺寸较小,所受热流场不均匀性的影响较小,故忽略了热压罐流场作用。后续开展大尺寸复合材料构件的固化仿真与优化时,则需要考虑热压罐流场作用。
| [1] |
YUE G Q, ZHANG B M, DAI F H, et al. Three-dimensional cure simulation of stiffened thermosetting composite panels[J]. Journal of Materials Science & Technology, 2010, 26(5): 467-471. |
| [2] |
YOO S H, HAN M G, HONG J H, et al. Simulation of curing process of carbon/epoxy composite during autoclave degassing molding by considering phase changes of epoxy resin[J]. Composites: Part B, 2015, 77: 257-267. DOI:10.1016/j.compositesb.2015.03.042 |
| [3] |
向炳东, 李敏, 李艳霞, 等. 筒状复合材料制件热压罐成型温度模拟及影响因素分析[J]. 航空学报, 2017, 38(11): 298-307. XIANG B D, LI M, LI Y X, et al. Numerical simulation and parameter analysis of temperature distribution of autoclave cured composite cylindrical structure[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(11): 298-307. |
| [4] |
李树健, 湛利华, 李常平, 等. 树脂基复合材料热压成型工艺数值模拟研究进展[J]. 宇航材料工艺, 2018, 48(1): 10-15. LI S J, ZHAN L H, LI C P, et al. Progress on numerical simulation for polymer matrix composite during hot pressing process[J]. Aerospace Materials and Technology, 2018, 48(1): 10-15. |
| [5] |
YUAN Z, WANG Y, YANG G, et al. Evolution of curing residual stresses in composite using multi-scale method[J]. Composites: Part B, 2018, 155: 49-61. DOI:10.1016/j.compositesb.2018.08.012 |
| [6] |
SHAH P H, HALLS V A, ZHENG J Q, et al. Optimal cure cycle parameters for minimizing residual stresses in fiber-reinforced polymer composite laminates[J]. Journal of Composite Materials, 2018, 52(6): 773-792. DOI:10.1177/0021998317714317 |
| [7] |
WANG H, CHEN L, YE F, et al. A multi-hierarchical successive optimization method for reduction of spring-back in autoclave forming[J]. Composite Structures, 2018, 188: 143-158. DOI:10.1016/j.compstruct.2018.01.010 |
| [8] |
STRUZZIERO G, SKORDOS A A. Multi-objective optimisation of the cure of thick components[J]. Composites: Part A, 2017, 93: 126-136. DOI:10.1016/j.compositesa.2016.11.014 |
| [9] |
DOLKUN D, ZHU W, XU Q, et al. Optimization of cure profile for thick composite parts based on finite element analysis and genetic algorithm[J]. Journal of Composite Materials, 2018, 52(28): 3885-3894. DOI:10.1177/0021998318771458 |
| [10] |
王俊敏, 郑志镇, 陈荣创, 等. 树脂基复合材料固化过程固化度场和温度场的均匀性优化[J]. 工程塑料应用, 2015, 41(4): 55-61. WANG J M, ZHENG Z Z, CHEN R C, et al. Curing degree field and temperature field uniformity optimization during curing process of resin matrix composites[J]. Engineering Plastics Application, 2015, 41(4): 55-61. DOI:10.3969/j.issn.1001-3539.2015.04.012 |
| [11] |
ZHAN S G, SHAN Y D, ZHANG B M. Temperature field of thick thermoset composite laminates during cure process[J]. Composites Science and Technology, 2005, 65: 517-523. DOI:10.1016/j.compscitech.2004.07.015 |
| [12] |
元振毅, 许英杰, 杨癸庚, 等. 基于多场耦合方法的厚截面复合材料固化过程优化研究[J]. 复合材料学报, 2021, 38(2): 526-535. YUAN Z Y, XU Y J, YANG G G, et al. Multi-objective optimization for curing process of thick composite based on multi-physics coupling method[J]. Acta Materiae Compositae Sinica, 2021, 38(2): 526-535. |
| [13] |
李雪芹, 刘刚, 张子龙, 等. 基于FBG应变监测的环氧树脂固化收缩及工艺参数优化[J]. 复合材料学报, 2016, 33(10): 2151-2157. LI X Q, LIU G, ZHANG Z L, et al. Curing shrinkage and process parameters optimization of epoxy resin based on FBG strain monitoring[J]. Acta Materiae Compositae Sinica, 2016, 33(10): 2151-2157. |
| [14] |
VAFAYAN M, BEHESHTY M H, GHOREISHY M H R, et al. The prediction capability of the kinetic models extracted from isothermal data in non-isothermal conditions for an epoxy prepreg[J]. Journal of Composite Materials, 2014, 48(9): 1039-1048. DOI:10.1177/0021998313482020 |
| [15] |
ABLIZ D, ARTYS T, ZIEGMANN G. Influence of model parameter estimation methods and regression algorithms on curing kinetics and rheological modelling[J]. Journal of Applied Polymer Science, 2017, 134(30): 45137. DOI:10.1002/app.45137 |
| [16] |
HAYATY M, BEHESHTY M H, ESFANDEH M. Cure kinetics of a glass/epoxy prepreg by dynamic differential scanning calorimetry[J]. Journal of Applied Polymer Science, 2011, 120(1): 62-69. DOI:10.1002/app.32982 |
| [17] |
BOGETTI T A, GILLESPIE J W. Two-dimensional cure simulation of thick thermosetting composites[J]. Journal of Composite Materials, 1991, 25(3): 239-273. DOI:10.1177/002199839102500302 |
| [18] |
闵荣, 元振毅, 王永军, 等. 基于黏弹性本构模型的热固性树脂基复合材料固化变形数值仿真模型[J]. 复合材料学报, 2017, 34(10): 2254-2262. MIN R, YUAN Z Y, WANG Y J, et al. Numerical simulation for curing deformation of resin matrix thermosetting composite using viscoelastic constitutive model[J]. Acta Materiae Compostitae Sinica, 2017, 34(10): 2254-2262. |
| [19] |
WIEMER H, SCHWARZENBERGER M, DIETZ G, et al. A holistic and doe-based approach to developing and putting into operation complex manufacturing process chains of composite components[J]. Procedia CIRP, 2017, 66: 147-152. DOI:10.1016/j.procir.2017.03.369 |
| [20] |
ZHAO J, ZHOU R. Particle swarm optimization applied to hypersonic reentry trajectories[J]. Chinese Journal of Aeronautics, 2015, 28(3): 822-831. DOI:10.1016/j.cja.2015.04.007 |
| [21] |
XU Y, ZHANG Q W, ZHANG W, et al. Optimization of injection molding process parameters to improve the mechanical performance of polymer product against impact[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(9/12): 2199-2208. DOI:10.1007/s00170-014-6434-y |
 2021, Vol. 49
2021, Vol. 49


