文章信息
- 王丽娜, 李志超, 武晓龙, 马丹丹, 杨平
- WANG Li-na, LI Zhi-chao, WU Xiao-long, MA Dan-dan, YANG Ping
- 高锰钢高速压缩时γ→ε-M和ε-M→α'-M的相变特征
- Transformation characteristics of γ→ε-M and ε-M→α'-M in high manganese steel under high speed compression
- 材料工程, 2021, 49(9): 101-108
- Journal of Materials Engineering, 2021, 49(9): 101-108.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2021.000323
-
文章历史
- 收稿日期: 2021-04-09
- 修订日期: 2021-06-15
2. 北京科技大学 钢铁共性技术协同创新中心, 北京 100083;
3. 北京科技大学 材料科学与工程学院, 北京 100083
2. Collaborative Innovation Center of Steel Technology, University of Science and Technology Beijing, Beijing 100083, China;
3. School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China
高锰相变诱发塑性(transformation induced plasticity, TRIP)钢在变形过程中能够发生丰富的马氏体相变,具有高的强度、塑性和应变硬化能力,可用于汽车冲击结构件的制备[1-5]。在高应变速率下高锰钢的相变行为和力学性能表现出新的特征,一些学者系统研究了应变速率对绝热剪切带形成机制和力学性能的影响[5-7],但均匀变形阶段的TRIP行为涉及较少。值得注意的是,高应变速率变形条件下更高的应力和温升可能影响高锰TRIP钢的相变动力学过程;相变取向依赖性的存在会导致不同取向晶粒的相变差异,从而表现出不同的应变硬化行为。这些高应变速率变形下马氏体相变的动力学和晶体学研究相对较少,因此有必要进行深入研究,为高锰TRIP钢在高速冲击条件下的应用提供理论依据。
形变诱发马氏体包括ε-M(六方马氏体)和α′-M(体心马氏体),α′-M可直接从γ(奥氏体)中产生,多数γ不锈钢中的马氏体是通过这种机制转变的[8]。马氏体转变也可分两个阶段完成,分别为γ→ε-M和ε-M→α′-M,高锰TRIP钢中的相变也是通过两阶段转变完成的[9]。γ→ε-M和ε-M→α′-M相变都是通过切变方式完成的,但是前者是沿〈112〉不全位错发生的切变[10-11],应与位错的分解、层错能有关,因此二者的动力学过程可能存在差异;同时在高锰TRIP钢中发现残余的ε-M,这说明γ→ε-M和ε-M→α′-M相变速率存在差异[9, 12-13]。γ的晶粒取向是影响高锰TRIP钢相变行为的重要因素之一。在静态变形条件下,形变诱发马氏体相变具有明显的取向依赖性[14-15]。高应变速率下,应变速率不同、形变量不同,在进行取向依赖性分析时需进行区分;此外,关于马氏体相变取向依赖性的研究多数仅考虑γ→ε-M阶段,未涉及ε-M→α′-M阶段。
综上所述,高速压缩高锰TRIP钢均匀变形区的相变行为对于高锰TRIP钢的组织和性能调控具有重要影响,多数TRIP行为的研究都未对γ→ε-M和ε-M→α′-M相变区分考虑,存在一定的局限性。本工作利用XRD和EBSD技术、相变晶体学计算对高锰TRIP钢在高速压缩变形条件下的γ→ε-M和ε-M→α′-M相变动力学特征、相变取向依赖性进行系统研究,阐明其机制的同时为高速变形条件下的TRIP行为控制、高锰TRIP钢的性能调控提供理论依据。
1 实验材料与方法以高锰TRIP钢作为实验材料,具体成分(质量分数/%)为:C 0.031,Mn 19.93,Si 3.30,Al 2.12,Fe余量。对铸锭进行锻造,始锻温度为1050 ℃,终锻温度为700~800 ℃。锻造后的样品在1050 ℃保温2.5 h进行固溶处理。利用CMT4305电子万能试验机和分离式霍普金森压杆分别对高锰TRIP钢进行室温压缩,应变速率分别为1×10-3 s-1和5×103 s-1,压缩试样的尺寸均为ϕ5 mm×5 mm。高速压缩时,限制试样的压缩变形量分别为20%,40%和52%。对试样进行打磨和抛光后,利用5%(体积分数)高氯酸酒精溶液进行电解抛光。利用Imager M2M型光学显微镜(OM)和QUANTA FEG 450扫描电子显微镜(SEM)进行微观组织表征,利用TSL OIM EBSD系统对压缩试样进行取向成像分析。利用D8 Advance X射线衍射仪对高锰TRIP钢样品进行物相测试。X射线衍射仪测得各衍射峰的积分强度可以确定γ, ε-M和α′-M的体积分数。但本实验涉及的压缩变形样品已形成强织构并影响各衍射峰的积分强度,使得定量计算的结果出现偏差。因此,本实验利用Topas软件进行结构精修和织构精修,拟合得到各相的体积分数。基于K-S关系的两阶段相变晶体学模型,对压应力与相变应变引起的机械功(相变机械功)进行计算,评价γ晶粒取向对马氏体(ε-M和α′-M)相变难易的影响。
2 结果与分析 2.1 高速压缩变形条件下的组织转变特征图 1为高锰TRIP钢在静态压缩(1×10-3 s-1)和高速压缩(5×103 s-1)后的显微组织。变形量为20%时,静态压缩样品的γ晶粒内观察到ε-M板条(见图 1(a)),高速压缩样品中的马氏体为ε-M和α′-M(见图 1(e))。变形量为40%时,静态压缩样品中的马氏体转变量明显增加(见图 1(b)),而高速压缩样品中的马氏体转变量无明显变化(见图 1(f))。变形量为52%时,静态压缩和高速压缩样品中均具有较多的马氏体,并且α′-M的量较多(见图 1(c), (g))。在静态压缩样品中已观察到裂纹的扩展、未出现绝热剪切带(见图 1(d))。高速压缩样品中未出现裂纹,在平行于样品边缘的方向观察到绝热剪切带(如图 1(h), (i)中箭头所示)。可见,高锰TRIP钢在不同应变速率变形条件下均发生显著的形变诱发马氏体相变。高速压缩样品中未出现裂纹的形核和扩展,这主要是由于绝热剪切带内的组织碎化、动态再结晶进一步提高了高锰TRIP钢的强度,抑制了裂纹的形核[5]。40%~52%静态和高速压缩样品已经表现出明显的形变不均匀性(局部的裂纹或强剪切),推测此时均匀变形区变形量减小、TRIP效应减弱。

|
图 1 高锰TRIP钢压缩变形后的组织 (a)20%静态压缩;(b)40%静态压缩;(c)52%静态压缩;(d)52%静态压缩样品中的裂纹;(e)20%高速压缩;(f)40%高速压缩;(g)52%高速压缩;(h)52%高速压缩样品中的绝热剪切带分布;(i)52%高速压缩中的绝热剪切带局部放大 Fig. 1 Microstructures of compressed high manganese TRIP steel (a)20% static compression; (b)40% static compression; (c)52% static compression; (d)crack in 52% static compressed sample; (e)20% high speed compression; (f)40% high speed compression; (g)52% high speed compression; (h)distribution of adiabatic shear bands in 52% high speed compressed sample; (i)amplification of adiabatic shear band in 52% high speed compressed sample |
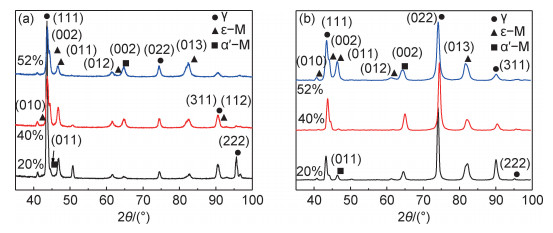
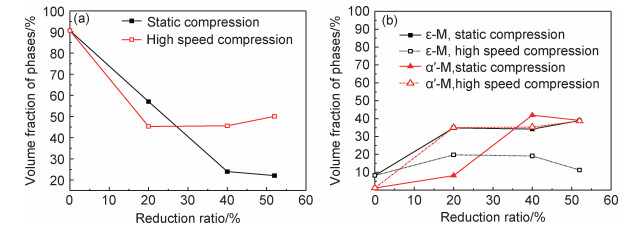
高锰TRIP钢的固溶样品以γ和ε-M为主,ε-M的体积分数约为8%。图 2为20%, 40%, 52%静态压缩和高速压缩样品的XRD图谱。利用Topas软件对图 2中的数据进行晶体结构和织构精修,全谱拟合得到各相的体积分数如图 3所示。在静态压缩条件下,20%压缩时γ, ε-M和α′-M的体积分数分别为57.04%, 34.83%和8.13%,主要发生了γ→ε-M相变,ε-M→α′-M相变不显著。变形量从20%增加至40%时,γ的体积分数减少了33%,α′-M的体积分数增加了34%,这表明γ→ε-M和ε-M→α′-M相变顺利发生。变形量增加至52%时,各相的体积分数变化不大,TRIP效应被抑制。在高速压缩条件下,20%压缩时γ, ε-M和α′-M的体积分数分别为45.29%, 19.74%和34.97%。与静态压缩相比,高速压缩有较少的残余γ(见图 3(a))、较多的α′-M(见图 3(b))。这说明在0%~20%压缩变形阶段,高应变速率提高了γ→ε-M和ε-M→α′-M相变的速率。变形量增加至40%时,高速压缩样品中各相的体积分数变化并不明显(如图 3所示),这表明γ→ε-M和ε-M→α′-M相变被抑制。变形量增加至52%时,各相的体积分数仍无显著变化。
|
图 2 高锰TRIP钢压缩变形后的XRD图谱 (a)静态压缩;(b)高速压缩 Fig. 2 XRD patterns of compressed high manganese TRIP steels (a)static compression; (b)high speed compression |
|
图 3 静态压缩和高速压缩高锰TRIP钢中三相的体积分数 (a)γ; (b)ε-M和α′-M Fig. 3 Volume fractions of three phases in static and high speed compressed high manganese TRIP steels (a)γ; (b)ε-M and α′-M |
上述可以看出,在静态压缩变形的初期以γ→ε-M相变为主。在高速压缩变形的初期发生显著的γ→ε-M和ε-M→α′-M相变。与静态压缩相比,高速压缩变形的马氏体相变尤其是ε-M→α′-M相变速率显著提高。在40%~52%静态压缩和高速压缩样品中,TRIP效应均被抑制。这与图 1(h), (i)中的结果一致,即此阶段高锰TRIP钢已经表现出明显的形变不均匀性,均匀变形区变形量减小、TRIP效应减弱。考量整个变形阶段,高速压缩变形保留了较多的残余γ(见图 3(a)),即抑制了γ→ε-M相变。52%高速压缩和静态压缩样品中的α′-M的体积分数接近,前者具有较少的残留ε-M(如图 3(b)所示),这说明高应变速率显著促进了ε-M→α′-M相变。综上所述,一方面高应变速率使得变形初期的马氏体相变速率显著提高;另一方面,应变速率的提高抑制了γ→ε-M相变,促进了ε-M→α′-M相变。
高锰TRIP钢的层错能较低,a/2〈110〉全位错可分解为两个a/6〈112〉不全位错。在应力作用下,间隔的{111}γ面沿〈112〉方向发生切动,产生ε-M,无体积膨胀。因此,形变诱发ε-M的产生需要两个条件,较低的层错能和较高的外应力。多数研究人员认为,高速变形时材料会有不同程度的温升、层错能的提高[16-19]以及应力的提高[6, 20]。高应变速率下层错能的提高限制不全位错的产生,使得γ→ε-M相变被抑制。ε-M→α′-M相变的晶格切变与不全位错无关,相变体积膨胀较大。因此,与γ→ε-M相比,ε-M→α′-M相变需克服更高的相变阻力(应变能),即ε-M→α′-M相变受外应力影响较大,高速变形时较高的应力可促进ε-M→α′-M相变的发生。ε-M→α′-M相变的组织分析同样表明,α′-M在ε-M板条碰撞的应力集中处优先出现,即高应力促进了ε-M→α′-M相变[9, 12]。综上可得,高速变形条件下的温升、层错能的提高使得γ→ε-M相变被抑制,高速变形时的高应力促进了ε-M→α′-M相变。
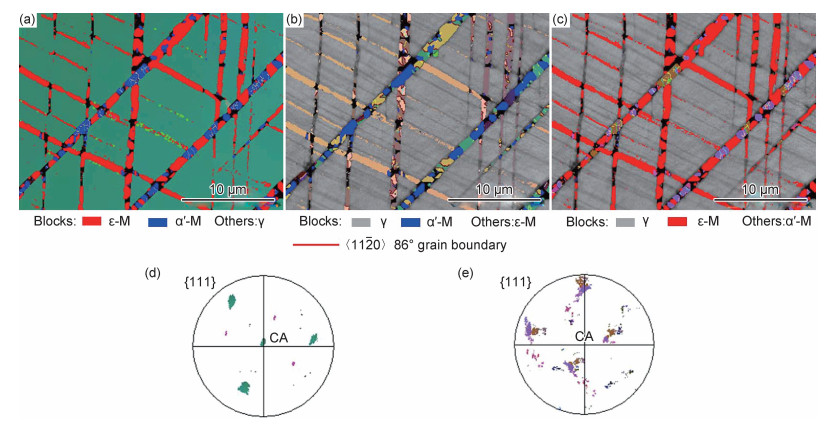
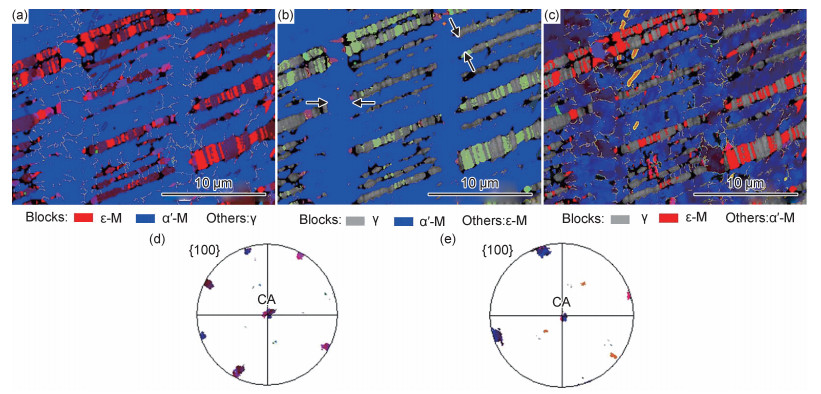
2.3 高速压缩变形条件下的取向依赖性分析取向依赖性是多晶体变形时的特征之一,高锰TRIP钢的相变取向依赖性会导致不同取向γ晶粒具有不同的相变速率、晶粒尺寸,从而造成不同的应变硬化行为。因此,基于低应变率下高锰TRIP钢相变取向依赖性的研究基础,对高应变速率下的相变取向依赖性进行研究。图 4和图 5分别为20%高速压缩样品中〈111〉γ和〈100〉γ晶粒的选区取向成像分析图。该〈111〉γ晶粒内的ε-M板条宽度约1 μm,ε-M板条内有少量α′-M形成。与〈111〉γ晶粒相比,图 5(b)中〈100〉γ晶粒内的ε-M板条较宽(箭头之间的板条),并且已经转变为尺寸较大且具有〈100〉取向的α′-M(如图 5(a)~(c)所示)。即20%高速压缩样品中,〈111〉γ晶粒内的γ→ε-M和ε-M→α′-M相变困难,马氏体转变量很少、无尺寸优势;〈100〉γ晶粒具有发生γ→ε-M和ε-M→α′-M相变的优势,马氏体转变量较多且ε-M和α′-M具有尺寸优势。
|
图 4 20%高速压缩样品中〈111〉γ晶粒的取向成像分析 (a)γ的取向成像图;(b)ε-M的取向成像图;(c)α′-M的取向成像图;(d)γ的极图;(e)α′-M的极图 Fig. 4 Orientation imaging analysis of 〈111〉γ grains in 20% high speed compressed high manganese TRIP steels (a)orientation map of γ; (b)orientation map of ε-M; (c)orientation map of α′-M; (d)pole figure of γ; (e)pole figure of α′-M |
|
图 5 20%高速压缩样品中〈100〉γ晶粒的取向成像分析 (a)γ的取向成像图;(b)ε-M的取向成像图;(c)α′-M的取向成像图;(d)γ的极图;(e)α′-M的极图 Fig. 5 Orientation imaging analysis of 〈100〉γ grains in 20% high speed compressed high manganese TRIP steels (a)orientation map of γ; (b)orientation map of ε-M; (c)orientation map of α′-M; (d)pole figure of γ; (e)pole figure of α′-M |
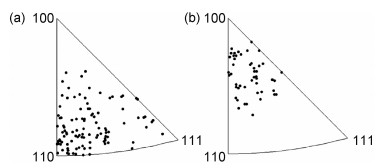
为提高马氏体相变取向依赖性分析的统计性,对20%高速压缩样品中的相变取向依赖性进行统计,如图 6所示。可以看出马氏体转变量小于45%(样品的马氏体平均转变量约为45%)时,对应的γ晶粒为非〈100〉取向并且集中分布在近〈110〉取向附近(见图 6(a))。马氏体转变量大于45%时,γ晶粒的取向为近〈100〉(见图 6(b))。即〈100〉为易发生马氏体相变的取向,Liu等[21]在静态压缩高锰TRIP钢的相变取向依赖性研究中得到类似的规律。
|
图 6 20%高速压缩高锰TRIP钢中具有不同马氏体体积分数(VM)的γ晶粒取向 (a)VM < 45%;(b)VM>45% Fig. 6 Orientations of γ grains with different volume fractions of martensite in 20% high speed compressed high manganese TRIP steels (a)VM < 45%;(b)VM>45% |
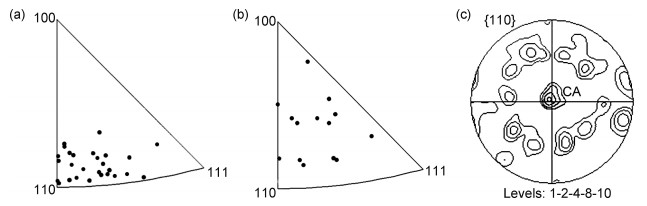
图 7为40%高速压缩样品的相变取向依赖性分析。与20%高速压缩样品相比,40%高速压缩样品内难发生马氏体相变的γ晶粒仍具有近〈110〉取向(见图 7(a)),但是马氏体转变量较大的γ晶粒取向偏离〈100〉(见图 7(b)),即相变取向依赖性减弱。由图 2~3的分析可知,20%~40%高速压缩阶段的TRIP行为被抑制,因此该阶段以形变为主。γ晶粒在压缩变形时会向稳定取向〈110〉转动[22],因此推测相变取向依赖性的减弱可能与γ晶粒的取向转动有关。图 7(c)为40%高速压缩样品内的γ织构,可以看出,此时γ形成了较强的〈110〉织构,这说明应变速率的增加并未显著降低马氏体相变的取向依赖性,但γ晶粒继续变形导致取向转动、形成〈110〉织构。
|
图 7 40%高速压缩高锰TRIP钢的马氏体相变取向依赖性 (a)VM < 45%的γ晶粒取向; (b)VM>45%的γ晶粒取向; (c)γ的极图 Fig. 7 Orientation dependence of martensitic transformation in 40% high speed compressed high manganese TRIP steels (a)γ grain orientations with VM less than 45%;(b)γ grain orientations with VM more than 45%;(c)pole figure of γ |
高锰TRIP钢在4个{111}γ面产生的4个ε-M变体记为ε1~ε4;根据γ和α′-M变体的K-S关系,24个α′-M变体记为V1~V24[23]。Humbert等[24]认为变体选择存在于γ→ε-M和ε-M→α′-M相变阶段,当应力与相变应变的交互作用功(相变机械功)超过某一临界值时,该变体有机会出现。应力引起的相变机械功可以用W=(1/2)σε来表示,式中:σ为局部应力;ε为相变应变沿应力方向的分量。不同取向γ晶粒内,马氏体变体的相变机械功不同,相变机械功最大的变体优先出现,因此,可以利用γ晶粒内各变体的相变机械功最大值进行取向依赖性分析。本工作基于K-S关系的两阶段马氏体相变晶体学模型[25],对压缩条件下不同取向γ晶粒内马氏体(ε-M和α′-M)变体的相变机械功最大值进行计算。同时结合实验数据分析γ晶粒取向对γ→ε-M和ε-M→α′-M相变难易的影响,即评价两阶段相变的取向依赖性规律。
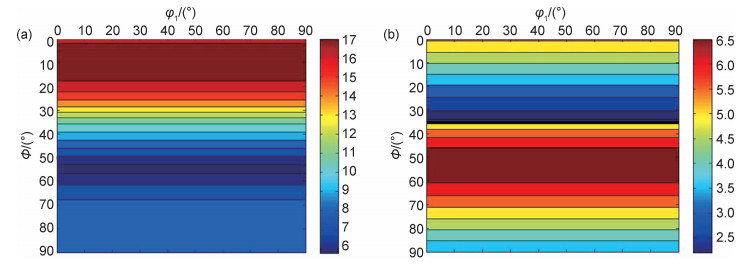
图 8(a)为采用φ2=45°取向分布函数(ODF)图表示各取向γ晶粒内ε-M相变机械功最大值。可以看出,近〈100〉γ晶粒的ε-M相变机械功最大(Φ=0°水平线),近〈111〉γ晶粒的ε-M相变机械功最小(Φ=55°水平线),前者应具有发生γ→ε-M相变的优势,后者则相变困难,这与图 4~6中的实验结果一致。这是由于每个ε-M变体沿不同方向产生相同大小的应变量,载荷方向与〈100〉γ晶粒中4个ε-M变体的应变收缩方向最小夹角为9.7°,载荷方向与〈111〉γ晶粒中4个ε-M变体的应变收缩方向最小夹角为55.1°,因此,外加载荷在〈100〉γ晶粒的ε-M变体应变收缩方向具有更大的分量,促进了γ→ε-M相变的发生。α′-M相变机械功的计算结果表明,〈111〉γ晶粒内的ε4变体优先发生ε-M→α′-M相变,α′-M相变机械功最大(如图 8(b)中Φ=55°水平线所示),但图 4中的实验数据表明〈111〉γ晶粒并不具备发生ε-M→α′-M相变的优势。这主要是由于〈111〉γ晶粒内γ→ε-M相变机械功小(如图 8(a)中Φ=55°水平线所示)、相变困难,因此,ε-M板条窄、数量少(见图 4(a)~(c)),进而抑制了ε-M→α′-M相变。即ε-M→α′-M相变的难易与ε-M, α′-M变体的相变机械功均有关。与〈111〉γ晶粒相比,〈100〉γ晶粒内ε-M板条对应的α′-M相变机械功略小(如图 8(b)中Φ=0°水平线所示),但却具有ε-M→α′-M相变的优势。这是由于〈100〉γ晶粒具有最大的ε-M相变机械功(如图 8(a)中Φ=0°水平线所示),因此,ε-M板条的数量多、尺寸大(见图 5(a), (b)),为后续的ε-M→α′-M相变提供有利的形核条件。综上可得,〈100〉γ晶粒具有发生γ→ε-M和ε-M→α′-M相变的优势。γ→ε-M相变的难易主要取决于ε-M相变机械功。ε-M→α′-M相变的难易则取决于两个因素,一是ε-M相变机械功的大小;二是α′-M相变机械功的大小。较大的ε-M和α′-M相变机械功共同促进ε-M→α′-M相变的发生。
|
图 8 单向压缩应力状态下φ2=45° ODF图中各取向γ晶粒内马氏体相变机械功的最大值(σ33=200 MPa) (a)γ→ε-M相变; (b)ε-M→α′-M相变 Fig. 8 Maximum mechanical work of martensitic transformation of γ grains in φ2=45° ODF under uniaxial compression (σ33=200 MPa) (a)γ→ε-M transformation; (b)ε-M→α′-M transformation |
(1) 在压缩变形条件下,5×103 s-1的高应变速率提高了γ的稳定性,抑制γ→ε-M相变,这是由于γ→ε-M相变主要受层错能的影响。高应变速率下具有较高的应力,促进了ε-M→α′-M相变,这是由于ε-M→α′-M相变需克服较大的相变阻力。
(2) 静态压缩变形的初期以γ→ε-M相变为主,高速压缩变形的初期发生显著的γ→ε-M和ε-M→α′-M相变。应变速率的提高使得马氏体相变速率显著提高。变形量大于40%时,静态和高速压缩样品已表现出明显的形变不均匀性,分别出现局部的裂纹和绝热剪切带。
(3) 高应变速率条件下,马氏体相变具有取向依赖性,〈100〉γ晶粒具有发生γ→ε-M和ε-M→α′-M相变的优势。γ→ε-M相变的难易取决于ε-M相变机械功的大小,而ε-M→α′-M相变的难易则取决于ε-M和α′-M相变机械功。
| [1] |
高绪涛, 赵爱民, 赵征志, 等. 热轧TRIP钢残余奥氏体及其稳定性研究[J]. 材料工程, 2011(11): 39-43. GAO X T, ZHAO A M, ZHAO Z Z, et al. Investigation of retained austenite and its stability in hot rolled TRIP steel[J]. Journal of Materials Engineering, 2011(11): 39-43. DOI:10.3969/j.issn.1001-4381.2011.11.009 |
| [2] |
SEVSEK S, BRASCHE F, MOLODOV D A, et al. On the influence of grain size on the TWIP/TRIP-effect and texture development in high-manganese steels[J]. Materials Science and Engineering: A, 2019, 754: 152-160. DOI:10.1016/j.msea.2019.03.072 |
| [3] |
GU X L, XU Y B, PENG F, et al. Role of martensite/austenite constituents in novel ultra-high strength TRIP-assisted steels subjected to non-isothermal annealing[J]. Materials Science and Engineering: A, 2019, 745: 318-329. |
| [4] |
孙秀荣, 王会珍, 杨平, 等. 不同结构金属高速压缩力学行为及微观剪切结构差异[J]. 金属学报, 2014, 50(4): 387-394. SUN X R, WANG H Z, YANG P, et al. Mechanical behaviors and micro-shear structures of metals with different structures by high-speed compression[J]. Acta Metallurgica Sinica, 2014, 50(4): 387-394. |
| [5] |
WANG H Z, SUN X R, YANG P, et al. Analysis of the transformation-induced plasticity effect during the dynamic deformation of high manganese steel[J]. Journal of Materials Science and Technology, 2015, 31(2): 191-198. DOI:10.1016/j.jmst.2014.03.027 |
| [6] |
HARIDAS R S, AGRAWAL P, THAPLIVAL S, et al. Strain rate sensitive microstructural evolution in a TRIP assisted high entropy alloy: experiments, microstructure and modeling[J]. Mechanics of Materials, 2021, 156: 103798-103814. DOI:10.1016/j.mechmat.2021.103798 |
| [7] |
LI J, YANG H Y, YANG P. Prolonged work hardening range in high manganese TRIP steel during adiabatic shear band formation[J]. Materials Letters, 2014, 134: 180-183. DOI:10.1016/j.matlet.2014.07.083 |
| [8] |
ZHANG M H, CHEN H Y, WANG Y K, et al. Deformation induced martensitic transformation kinetics and correlative micromechanical behavior of medium Mn transformation induced plasticity steel[J]. Journal of Materials Science and Technology, 2019, 35: 1779-1786. DOI:10.1016/j.jmst.2019.04.007 |
| [9] |
王会珍, 杨平, 毛卫民. 板条状马氏体形貌和惯习面的3D EBSD分析[J]. 材料工程, 2013(4): 74-80. WANG H Z, YANG P, MAO W M. 3D EBSD analysis of morphology and habit plane for lath martensite[J]. Journal of Materials Engineering, 2013(4): 74-80. DOI:10.3969/j.issn.1001-4381.2013.04.014 |
| [10] |
MAHAJAN S, GREEN M L, BRASEN D. A model for the FCC→HCP transformation, its applications, and experimental evidence[J]. Metallurgical Transactions A, 1977, 8(2): 283-293. DOI:10.1007/BF02661642 |
| [11] |
YANG J H, WAYMAN C M. On secondary variants formed at intersections of ε-martensite variants[J]. Acta Metallurgica, 1992, 40(8): 2011-2023. DOI:10.1016/0956-7151(92)90187-J |
| [12] |
鲁法云, 杨平, 孟利, 等. Fe-22Mn TRIP/TWIP钢拉伸过程组织、性能及晶体学行为分析[J]. 金属学报, 2013, 49(1): 1-9. LU F Y, YANG P, MENG L, et al. Microstructure, mechanical properties and crystallography analysis of Fe-22Mn TRIP/TWIP steel after tensile deformation[J]. Acta Metallurgica Sinica, 2013, 49(1): 1-9. |
| [13] |
SOUZA FILHO I R, SANDIM M J R, COHEN R, et al. Magnetic properties of a 17.6 Mn-TRIP steel: study of strain-induced martensite formation, austenite reversion, and athermal α'-formation[J]. Journal of Magnetism and Magnetic Materials, 2019, 473: 109-118. DOI:10.1016/j.jmmm.2018.10.034 |
| [14] |
HOU P J, LI Y, CHAE D, et al. Role of ferrite in the texture development, plastic anisotropy, martensitic transformation kinetics, and stress partitioning[J]. Materialia, 2021, 15: 100952-100972. DOI:10.1016/j.mtla.2020.100952 |
| [15] |
KANG J Y, KIM H, KIM K I. Effect of austenitic texture on tensile behavior of lean duplex stainless steel with transformation induced plasticity (TRIP)[J]. Materials Science and Engineering: A, 2017, 681: 114-120. DOI:10.1016/j.msea.2016.11.001 |
| [16] |
TALONEN J, HÄNNINEN H, NENONEN P, et al. Effect of strain rate on the strain-induced γ→α'-martensite transformation and mechanical properties of austenitic stainless steels[J]. Metallurgical and Materials Transactions A, 2005, 36(2): 421-432. DOI:10.1007/s11661-005-0313-y |
| [17] |
HE Z P, YANG H Y, HE Y L, et al. Influence of manganese on deformation behavior of lightweight steel at different strain rate[J]. Journal of Materials Research and Technology, 2020, 9(5): 11611-11621. DOI:10.1016/j.jmrt.2020.08.020 |
| [18] |
LI X, CHEN L, ZHAO Y, et al. Influence of manganese content on ε-/α'-martensite transformation and tensile properties of low-C high-Mn TRIP steels[J]. Materials & Design, 2018, 142: 190-202. |
| [19] |
ALLAIN S, CHATEAU J P, BOUAZIZ O, et al. Correlations between the calculated stacking fault energy and the plasticity mechanisms in Fe-Mn-C alloys[J]. Materials Science and Engineering: A, 2004, 387/389: 158-162. DOI:10.1016/j.msea.2004.01.059 |
| [20] |
BENZING J T, POLING W A, PIERCE D T, et al. Effects of strain rate on mechanical properties and deformation behavior of an austenitic Fe-25Mn-3Al-3Si TWIP-TRIP steel[J]. Materials Science and Engineering: A, 2018, 711(10): 78-92. |
| [21] |
LIU T Y, YANG P, MENG L, et al. Influence of austenitic orientation on martensitic transformations in a compressed high manganese steel[J]. Journal of Alloys and Compounds, 2011, 509: 8337-8344. DOI:10.1016/j.jallcom.2011.05.015 |
| [22] |
MENG L, YANG P, XIE Q G, et al. Dependence of deformation twinning on grain orientation in compressed high manganese steels[J]. Scripta Materialia, 2007, 56(11): 931-934. DOI:10.1016/j.scriptamat.2007.02.028 |
| [23] |
MIYAMOTO G, IWATA N, TAKAYAMA N, et al. Quantitative analysis of variant selection in ausformed lath martensite[J]. Acta Materialia, 2012, 60(3): 1139-1148. DOI:10.1016/j.actamat.2011.11.018 |
| [24] |
HUMBERT M, PETIT B, BOLLE B, et al. Analysis of the γ-ε-α' variant selection induced by 10% plastic deformation in 304 stainless steel at -60 ℃[J]. Materials Science and Engineering: A, 2007, 454/455: 508-517. DOI:10.1016/j.msea.2006.11.112 |
| [25] |
SCHUMANN H. Kristall geometrie[M]. Leipzig: VEB Deutscher Verlag für Grundstoffindustrie, 1979: 137-141.
|
 2021, Vol. 49
2021, Vol. 49

