文章信息
- 李晓宇, 姜良宝, 刘家希, 王敏博, 李佳明, 颜悦
- LI Xiao-yu, JIANG Liang-bao, LIU Jia-xi, WANG Min-bo, LI Jia-ming, YAN Yue
- 化学强化铝硅酸盐玻璃表面微观力学行为的有限元模拟
- Finite element modelling of surface micromechanical behavior on chemically strengthened aluminosilicate glass
- 材料工程, 2021, 49(7): 148-157
- Journal of Materials Engineering, 2021, 49(7): 148-157.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2021.000050
-
文章历史
- 收稿日期: 2021-01-19
- 修订日期: 2021-04-11
2. 北京市先进运载系统结构透明件工程技术研究中心, 北京 100095
2. Beijing Engineering Research Center of Advanced Structural Transparencies for the Modern Traffic System, Beijing 100095, China
化学强化铝硅酸盐玻璃因其高强度、高硬度和良好的抗冲击性能,广泛应用于飞机、高铁风挡及触摸屏屏幕等领域[1-3]。化学强化,又称离子交换,是熔融盐液中半径较大的碱金属离子与玻璃表面半径较小的碱金属离子发生互扩散从而产生表面压应力的过程。作为触摸屏屏幕或飞机、高铁风挡玻璃的主要材料,化学强化玻璃的表面抗损伤性能非常重要,表面硬度和模量与玻璃的抗损伤性能息息相关,通常作为评判化学强化玻璃抗损伤性能的关键指标。
纳米压痕方法是测量玻璃表面硬度和模量最为简单有效的方式。采用纳米压痕方法研究材料的力学性能,需要准确理解材料的应力-应变曲线和压痕加载-卸载曲线之间的关系[4]。纳米压痕过程中的很多参数,包括屈服应力、塑性变形区域、压痕应力场分布状态等均难以通过实验获得[5-6],这些参数的分析方法主要有解析法和数值法两类,而由于应力场的复杂性,解析法通常只能解决少量简单问题,所以数值法已成为不可替代的广泛应用的方法。有限元法就是伴随着电子计算技术的进步发展起来的新兴数值分析方法。利用有限元模拟能够更好地理解纳米压痕过程中弹塑性变形及残余应力场的变化[7],并且能够计算出一些难以通过实验测量的塑性参数,例如脆性材料的屈服强度、塑性区域应力应变关系等[8],对于研究脆性材料弹塑性变形行为、预测其力学性能具有重要科学意义。
采用有限元方法研究脆性材料在压痕过程中的弹-塑性变形行为的报道很多[9-17]。描述压痕应力场的模型中,最基本的两个模型是Yoffe[9]模型和Chiang,Marshall,Evans的CME[10]模型。Yoffe通过无限弹性介质中心点扩张理论来获得压痕过程中的弹性应力。CME模型通过空洞扩张理论将塑性区域尺寸与材料力学参数联系起来。后来,Laursen和Simo[11]在前人基础上,采用有限元方法计算了压痕过程中的应力场,指出有限元方法能够获得实验难以获得的多项参数。这些计算和模拟均基于压头为理想锥形的假设,即忽略了真实压头形状对压痕过程的影响。1994年,Giannakopoulos等[12]采用有限元方法模拟了金属材料维氏压头的压痕过程,考虑了真实压头的几何形状以及材料塑性区域应力应变关系对压痕的影响,并计算了维氏压头压痕过程中的应力分布。Larsson等[13]在1996年采用同样的方法模拟了金属材料玻氏压头的压痕过程,并对玻氏压头压痕过程中的力学理论基础展开了深入的研究。Zeng等[14]根据Giannakopoulos和Larsson的模型,对多种性能差异很大的材料(包括金属材料、脆性材料等)压痕过程进行了有限元模拟,并与实验结果进行对比,发现有限元能够很好地模拟材料压痕过程。Li等[15]采用有限元方法研究了石英玻璃在纳米压痕过程中致密化现象对其变形的影响。Kang等[16]采用有限元方法研究了玻璃表面残余应力对纳米压痕过程中裂纹萌生及扩展过程的影响。
尽管针对硅酸盐玻璃压痕过程的有限元模拟研究成果很多,但这些研究大都集中于未经化学强化的原片硅酸盐玻璃,对于经过化学强化后,表面具有压应力层的硅酸盐玻璃的压痕过程研究很少。此外,采用浮法工艺生产的硅酸盐玻璃由于下表面与锡液接触会发生渗锡现象,造成浮法玻璃上下两表面的成分和结构有所差异,通常称之为空气面和锡面,空气面和锡面在纳米压痕加载-卸载过程中的表现有所差异,针对两表面压痕过程差异性的有限元模拟研究鲜见报道。
本工作以化学强化浮法铝硅酸盐玻璃作为研究对象,采用纳米压痕方法对化学强化铝硅酸盐玻璃加载-卸载过程中的力学行为展开实验研究,并采用有限元方法对化学强化铝硅酸盐玻璃在纳米压痕实验过程中的加载-卸载曲线进行分析,与实验结果进行对照,同时采用有限元方法对纳米压痕实验过程中无法获得的玻璃应力-应变曲线、屈服应力、压痕应力场等参数进行计算分析,为化学强化铝硅酸盐玻璃弹塑性变形行为研究提供理论依据。
1 实验材料与方法 1.1 样品制备实验采用2.2 mm厚的浮法铝硅酸盐玻璃样品,其成分见表 1。化学强化过程在离子交换炉(XFT-2500)中进行,采用纯度大于99.9%的纯硝酸钾熔盐进行强化。实验样品分两组,其化学强化温度分别为450 ℃和500 ℃,化学强化时间均为1 h。化学强化后采用锡面仪对每个样品的“空气面”和“锡面”进行区分及标记,并采用表面应力仪(FSM-6000LE)对样品两表面的表面压应力(compressive stress,CS)和应力层深度进行测试(图 1),表面压应力和应力层深度测试结果见表 2。
| SiO2 | Al2O3 | MgO | Na2O | K2O | CaO | Fe2O3 | Other |
| 63.5 | 5.8 | 10.8 | 13.2 | 5.9 | 0.3 | 0.1 | Bal |

|
图 1 表面压应力和应力层深度测试 Fig. 1 Compressive stress and depth of stress layer testing |
| Ion-exchange temperature/℃ | Side | Compressive stress/MPa | Depth of stress layer/μm |
| 450 | Air side | 732 | 17 |
| Tin side | 748 | 15 | |
| 500 | Air side | 526 | 22 |
| Tin side | 538 | 20 |
纳米压痕采用Hysitron公司生产的原位纳米力学测试系统(TI 950)进行,设备载荷最大量程为10 mN。压痕实验采用玻氏压头(Berkovich indenter)进行,图 2为典型纳米压痕形貌图。每个样品的“空气面”和“锡面”均进行5次重复压痕实验,表面硬度和杨氏模量测试结果见表 3。样品的泊松比为0.25。

|
图 2 典型纳米压痕形貌图 Fig. 2 Typical image of nanoindentation |
| Ion-exchange temperature/℃ | Side | Hardness/GPa | Young’s modulus/GPa |
| 450 | Air side | 7.26±0.11 | 73.5±0.58 |
| Tin side | 7.45±0.05 | 75.6±0.83 | |
| 500 | Air side | 7.23±0.04 | 74.3±0.82 |
| Tin side | 7.25±0.05 | 74.4±0.42 |
纳米压痕的有限元模拟(FEM)有三维模拟和二维模拟两种。据文献报道[14-15],三维有限元模拟在对裂纹萌生与发展的预测中具有不可替代的作用,而对于纳米压痕加载-卸载曲线的模拟结果与二维有限元模拟非常接近。由于本工作仅对纳米压痕加载-卸载曲线及相关参数进行研究,且二维有限元模拟计算量小、计算时间短,因此采用二维有限元进行模拟。模拟采用商业软件ABAQUS 6.14进行。
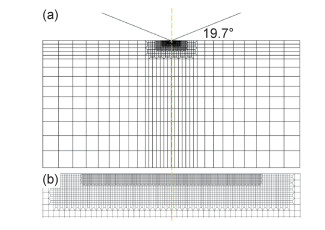
1.3.1 建立模型首先建立轴对称二维有限元模型(图 3),玻璃试样尺寸设定为半径100 μm,高100 μm的圆柱形试样,该尺寸能够保证模拟结果不受外边界约束条件变化的影响。进行有限元分析时,选用线性轴对称积分单元(CAX4)[18]对材料进行划分,在单元尺寸发生改变的过渡区域采用多点约束方式定义[19]。图 3给出了典型的网格划分示意图。为了获得精确的塑性变形和接触面积,压头下变形区域的网格必须划分得足够细致,远离压头区域的网格可以逐渐变疏,在保证精度的前提下减小计算量。同时,单元形状尽量保持正方形或长宽比尽量小的矩形以确保精度,整个试样由2940个四边形单元组成。采用圆锥形压头,圆锥母线与中轴夹角ϕ=70.3°,以确保圆锥形压头与纳米压痕实验采用的玻氏压头有相同的截面积-深度比。由于金刚石压头的硬度及杨氏模量比玻璃高出很多,模拟时将压头视为刚体。考虑到轴对称情况,为减少计算量,仅对1/2模型进行模拟,设置边界条件时,对称轴上施加r方向位移约束,材料底部设置为不可变形,外边界视为自由表面,边界条件设置情况见图 4。压头与样品之间视为无摩擦[20],压头采用位移加载。
|
图 3 有限元网格划分示意图 (a)整体网格;(b)接触区域细分网格 Fig. 3 Schematic diagrams of finite element mesh (a)entire mesh; (b)details of the mesh in the region of contact |

|
图 4 模型边界条件设置情况 Fig. 4 Boundary condition of the model |
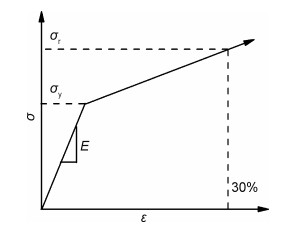
脆性材料在压应力作用下开裂前存在弹性变形和塑性变形两个阶段[13],因此,除弹性性质外,纳米压痕模拟过程中需输入玻璃材料的塑性参数。模拟时玻璃材料属性设定为均匀、各向同性,其应力-应变曲线选用双线性模型[12],认为玻璃在屈服前按照杨氏模量变化,屈服后的应力应变关系采用发生30%塑性应变时对应的应力(σr)来描述[12],如图 5所示。
|
图 5 玻璃的应力-应变曲线 Fig. 5 Stress-strain curve of glass |
其中,σ代表应力,ε代表应变。杨氏模量E由纳米压痕实验获得,泊松比υ取0.25。模拟采用的屈服准则为Von Mises屈服准则。对于陶瓷材料,通常认为屈服应力σy=0.48H(H代表硬度)[11-12],因此根据纳米压痕实验获得的玻璃硬度值能够得到玻璃的屈服应力。玻璃屈服之后的应力应变关系由参数决定。根据Larsson[10]给出的均匀、各向同性材料在玻氏压头下发生弹塑性变形时的解,压痕过程中施加的载荷可以表达为式(1):

|
(1) |
式中:P为施加的载荷;h为压入深度。
平均应力pav,即硬度,定义为施加的载荷与接触面积之间的比值,可以由式(2)得到:

|
(2) |
根据纳米压痕实验得到的硬度、杨氏模量值,以及根据硬度计算出的屈服应力值,代入式(2),即可获得σr,将σy和σr作为玻璃材料的塑性参数输入软件中进行计算。
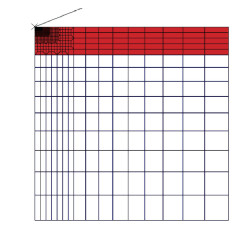
1.3.3 表面应力层的施加化学强化玻璃表面压应力层的模拟是通过施加预定义应力场实现的。图 6给出了施加预定义应力场后的应力情况示意图, 红色部分代表化学强化玻璃的压应力层。施加的预定义应力场深度为15 μm,与试样真实应力层深度一致。由于压入深度较浅(小于2 μm),因此将应力场设定为均匀分布,不考虑应力随深度的变化。
|
图 6 化学强化玻璃预定义应力场示意图 Fig. 6 Schematic diagram of the pre-defined stress field for the ion-exchanged glass |
有限元模拟输出的结果包括加载和卸载过程的载荷-位移曲线、接触面积及压痕应力场等。根据获得的载荷-位移曲线,采用Oliver-Pharr(OP)的方法,即可计算玻璃硬度和杨氏模量值。采用OP方法计算硬度和杨氏模量,需首先根据式(3)对卸载曲线进行指数拟合:
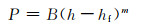
|
(3) |
式中:B和m为指数拟合参数;hf为完全卸载后获得的压痕残余深度。
根据式(3)指数拟合得到的参数,代入式(4),能够得到材料的刚度S:
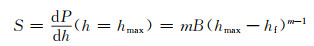
|
(4) |
式中:hmax是最大压入深度。压头与样品之间的接触深度hc可以通过式(5)得到:
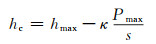
|
(5) |
式中:Pmax为最大压入载荷;κ是依赖于压头几何形状的参数,对于玻氏压头,κ=0.75。
根据hc,可以获得压痕接触面积。纳米压痕实验前,通常采用标准石英样块进行校正,在石英样块表面进行上百次压痕实验,通过经验参数拟合,得到真实压痕接触面积与接触深度的关系。而本工作模拟采用的压头为理想圆锥,根据其几何形状,其接触面积为A=πhc2tan2ϕ,其中ϕ=70.3°。因此,接触面积可以通过式(6)得到:
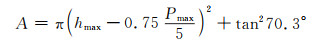
|
(6) |
硬度和折合模量可以分别通过式(7),(8)获得:

|
(7) |
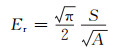
|
(8) |
折合模量与压头、样品的杨氏模量、泊松比有关:
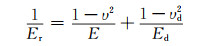
|
(9) |
式中:E和υ为样品的杨氏模量和泊松比;Ed和υd为金刚石压头的杨氏模量和泊松比。由于模拟过程中将压头视为刚体,即Ed=∞。因此,杨氏模量可以表达为:

|
(10) |
根据式(5)~(10),即可通过模拟获得的载荷-位移曲线计算出材料的硬度和杨氏模量值。
2 结果与分析 2.1 屈服应力与载荷-位移曲线模拟玻璃纳米压痕过程之前,首先需要根据纳米压痕实验获得的硬度值计算出玻璃的屈服应力。纳米压痕实验得到的化学强化前原片玻璃空气面硬度值为6.40 GPa,根据σy=0.48H的关系,可以得到原片玻璃空气面的屈服应力为σy=3.07 GPa。同样地,实验得到的原片玻璃锡面硬度值为6.41 GPa,可以得到锡面屈服应力为σy=3.08 GPa。将玻璃空气面的屈服应力σy=3.07 GPa,硬度H=pav=6.40 GPa,以及杨氏模量E=71.7 GPa值代入式(2),即可获得原片玻璃空气面σr=8.41 GPa。同样地,将玻璃锡面的屈服应力σy=3.08 GPa,硬度H=pav=6.41 GPa,以及杨氏模量E=72.7 GPa值代入式(2),得到原片玻璃锡面σr=8.35 GPa。将计算得到的σy和σr值输入ABAQUS软件塑性参数中,即可对纳米压痕过程进行计算。
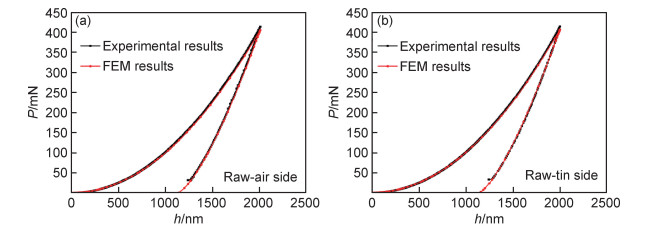
图 7对比了原片铝硅酸盐玻璃纳米压痕实验获得的载荷-位移曲线与有限元计算得到的载荷-位移曲线。从图中可以看出,原片铝硅酸盐玻璃通过有限元获得的载荷-位移曲线与实验得到的载荷-位移曲线之间重合度非常好。有限元模拟采用的是位移加载,即位移为固定值。当压头压入深度达到设定位移时,有限元计算得到的最大加载载荷与实验设定的最大载荷之间相对误差小于2%。影响有限元模拟结果的几个重要的参数包括杨氏模量、泊松比、屈服应力和塑性区域应力应变关系(即σr),分别输入空气面和锡面对应的参数后,两个表面的有限元模拟结果都与实验结果吻合度高。
|
图 7 原片铝硅酸盐玻璃纳米压痕实验与有限元计算得到的载荷-位移曲线的对比 (a)空气面; (b)锡面 Fig. 7 FEM calculated and experimentally measured indentation P-h curves for raw glass (a)air side; (b)tin side |
有限元模拟得到的载荷-位移曲线与实验得到的载荷-位移曲线的一致性说明有限元方法能够准确模拟铝硅酸盐玻璃的纳米压痕过程,铝硅酸盐玻璃的弹塑性本构精确符合图 5的双线性模型。同时,这一结果也说明通过式(2)计算得到的屈服应力及塑性区域应力应变关系与玻璃真实的塑性参数之间吻合度很高。脆性材料的塑性性质很难通过实验获得,有限元模拟可以用来验证由理论计算得到的玻璃塑性参数的准确性。此外,计算得出的玻璃塑性参数与文献报道[12]的结果十分接近,说明计算结果准确度较高。
图 8给出了具有不同表面压应力的化学强化玻璃纳米压痕实验与有限元模拟得到的载荷-位移曲线的对比。图 8(a),(b)分别给出的是在450 ℃下强化1 h的化学强化玻璃空气面和锡面的载荷-位移曲线,其表面压应力分别为732 MPa和748 MPa。图 8(c),(d)分别给出的是在500 ℃下强化1 h的化学强化玻璃空气面和锡面的载荷-位移曲线,其表面压应力分别为526 MPa和538 MPa。采用施加预定义应力场的方法模拟出的化学强化玻璃载荷-位移曲线与实验结果非常接近,当压入同一深度时,有限元计算得到的最大载荷与实验施加的最大载荷之间相对误差小于2%,有限元计算结果能够良好反应化学强化玻璃的纳米压痕过程。

|
图 8 不同表面压应力的化学强化铝硅酸盐玻璃纳米压痕实验与有限元模拟计算得到的载荷-位移曲线的对比 (a)732 MPa,空气面;(b)748 MPa,锡面;(c)526 MPa,空气面;(d)538 MPa,锡面 Fig. 8 FEM calculated and experimentally measured indentation P-h curves for ion-exchanged glass with different CS (a)732 MPa, air side; (b)748 MPa, tin side; (c)526 MPa, air side; (d)538 MPa, tin side |
图 9对比了有限元模拟的原片玻璃和具有不同表面压应力的化学强化玻璃的压痕载荷-位移曲线。从图中可以看出,当样品表面存在预定义压应力场时,载荷-位移曲线会产生明显的变化。压应力越大,压入相同深度所需载荷越大,说明表面压应力可以抵抗压头的压入。这一计算结果与实验结果一致。采用有限元方法能够准确分析压应力场对铝硅酸盐玻璃表面微观力学行为的影响规律。

|
图 9 有限元获得的原片玻璃与不同压应力化学强化玻璃压痕载荷-位移曲线 (a)空气面;(b)锡面 Fig. 9 Indentation load-displacement curves obtained from FEM for raw and ion-exchanged glasses with different CS (a)air side; (b)tin side |
图 10给出了原片铝硅酸盐玻璃和具有不同表面压应力的化学强化铝硅酸盐玻璃加载过程中压头接触面积随压入深度的变化。从放大的插图中可以看出,原片玻璃的接触面积比化学强化玻璃的接触面积大,接触面积随压应力的增大而减小,这是因为玻璃表面大的残余压应力能够抵抗压头的压入造成的[21]。

|
图 10 原片玻璃与具有不同表面压应力的化学强化玻璃加载过程中接触面积随压入深度的变化(插图为最大压入深度时接触面积的放大图) (a)空气面;(b)锡面 Fig. 10 Variation of contact area with indentetion depth during loading of raw and ion-exchanged glasses with different CS (the insets are the enlargement of the final contact area) (a)air side; (b)tin side |
如2.1节中的结果所示,有限元模拟能够精确描述原片玻璃与化学强化玻璃的压痕载荷-位移曲线。根据有限元模拟得到的载荷-位移曲线,计算了玻璃的硬度和杨氏模量,并与实验获得的硬度、杨氏模量值进行了对比分析。
首先根据式(3),对每一条有限元获得的载荷-位移曲线的卸载曲线部分进行指数拟合,然后将获得的指数拟合参数(B,m)及相关的压入深度参数代入式(4)~(10),即可得出不同玻璃样品的硬度与杨氏模量值。不同样品指数拟合参数及硬度、杨氏模量的计算结果见表 4。指数参数m是描述卸载曲线形状的一个重要参数,据文献报道,大部分金属和陶瓷材料在采用玻氏压头进行压痕实验时,其卸载曲线指数拟合获得的参数m都在1.2~1.5范围内变化[20]。从表 4中可以看出,不同玻璃样品的m值在1.22~1.37之间改变,与文献报道一致,说明有限元分析结果与实验结果吻合度较高。
| Sample | B/107 | m | S/105 Pa | A/10-11 m2 | H/GPa | E/GPa |
| Raw-air | 5.35 | 1.34 | 6.26 | 5.68 | 7.10 | 69.1 |
| Raw-tin | 1.11 | 1.22 | 6.25 | 5.62 | 7.25 | 69.3 |
| 526-air | 5.14 | 1.34 | 6.19 | 5.38 | 7.96 | 70.1 |
| 538-tin | 3.28 | 1.30 | 6.24 | 5.35 | 8.05 | 70.9 |
| 732-air | 4.02 | 1.32 | 6.25 | 5.36 | 8.10 | 71.0 |
| 748-tin | 7.66 | 1.37 | 6.38 | 5.36 | 8.21 | 72.5 |
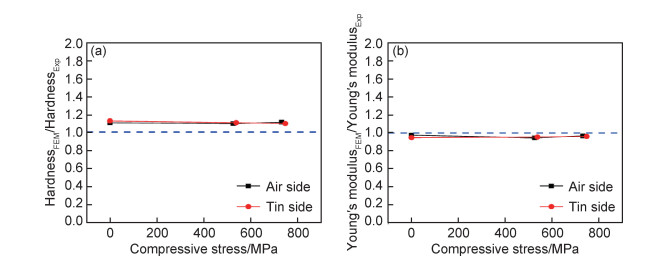
为更好地对比根据有限元结果计算出的硬度、杨氏模量值与实验得到的硬度、杨氏模量值之间的差异,图 11给出了不同压应力的玻璃样品模拟结果与实验结果之间的比值。从图 11可以看出,对于不同压应力的玻璃样品,根据有限元结果计算出的硬度值与实验得到的硬度值的相对误差为10%,而根据有限元结果计算出的杨氏模量值与实验值的相对误差为2%。
|
图 11 根据有限元结果计算的硬度值与实验硬度的比值(a)和根据有限元结果计算的杨氏模量值与实验杨氏模量的比值(b)随压应力的变化 Fig. 11 Ratio between hardness derived from the finite element results and from experimental results (a) and Young's modulus derived from the finite element results and from experimental results (b) as a function of compressive stress |
根据有限元模拟得到的载荷-位移曲线计算出的硬度值相比纳米压痕实验得出的硬度值略微偏大,造成这一结果的主要原因在于实验设备计算硬度时采用的接触面积与根据有限元结果计算时采用的接触面积不同。实验设备采用的接触面积是通过金刚石压头在标准熔融石英标样上经过上百次压痕实验后,拟合得到的接触面积关于压入深度的经验公式(如式(11)所示),能够更好地体现出压头的真实形状,例如压头在使用过程中产生磨损,采用实验方法能够将磨损后的压头产生的真实接触面积准确计算出来。然而有限元模拟采用的是理想圆锥压头,接触面积是根据圆锥的几何形状计算出的理想接触面积,理想圆锥压头在尖端处没有曲率,相比实验所用真实压头,必然会产生一个较小的接触面积,导致计算得出的硬度值偏大。有限元计算得到的杨氏模量值与实验值接近,略微偏小,产生这一偏差的原因在于压痕设备在计算杨氏模量时采用的是真实金刚石杨氏模量和泊松比,而有限元模拟过程中假设压头是完全刚性的,即与被压材料相比,压头杨氏模量视为无穷大,因此接触面积的差异以及压头完全刚性的假设导致杨氏模量计算结果与实验结果之间也存在一定偏差,但偏差非常小,说明有限元拟合结果能够很好地预测铝硅酸盐玻璃的表面微观力学性能。

|
(11) |
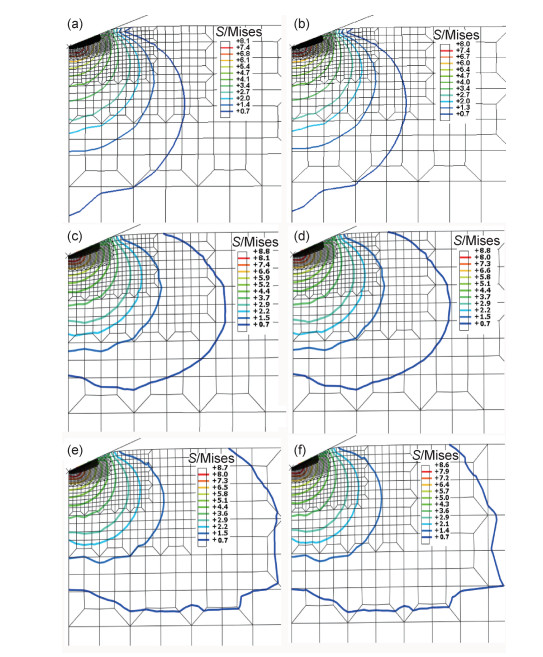
图 12给出了原片玻璃和化学强化玻璃完全加载时的压痕截面及Von Mises应力分布情况。纳米压痕过程中,被压入材料易在压痕周围产生材料堆积现象(pile-up)。表面材料堆积会导致计算接触面积时产生明显的偏差,进而影响到硬度、杨氏模量计算结果的准确度。从图 12可以看出,原片玻璃和化学强化玻璃均没有发生表面材料堆积现象。
|
图 12 原片玻璃和化学强化玻璃完全加载时Von Mises应力分布情况 (a)原片玻璃,空气面;(b)原片玻璃,锡面;(c)526 MPa,空气面;(d)538 MPa,锡面;(e)732 MPa,空气面;(f)748 MPa,锡面 Fig. 12 Von Mises stress distributions at fully loaded of raw and ion-exchanged glasses (a)raw glass, air side; (b)raw glass, tin side; (c)526 MPa, air side; (d)538 MPa, tin side; (e)732 MPa, air side; (f)748 MPa, tin side |
研究压痕过程中的应力分布状态能够更好地理解压痕实验中的物理现象。图 12反映了化学强化后残余压应力对压痕过程中压头下方应力场的大小和分布的影响。对比原片及化学强化玻璃在完全加载时Von Mises应力可知,残余压应力对压痕应力场的大小及分布状态有显著影响。Von Mises应力最大值出现在最接近压头下方的位置。从图 12(a), (b)可以看出,原片玻璃空气面和锡面的Von Mises应力最大值分别为8.1 GPa和8.0 GPa,从图 12(c)~(f)中可以看出,化学强化后玻璃空气面和锡面的Von Mises应力最大值增大至8.6~8.8 GPa之间。化学强化玻璃的表面残余压应力使得玻璃在压痕过程中产生的Von Mises应力增大。此外,化学强化前后Von Mises应力分布状态也有较大改变。据文献报道,接近压头下方的近场Mises应力与材料的塑性区域相关[14]。对比原片玻璃与化学强化玻璃的近场应力,发现二者区别很小,说明化学强化对玻璃的塑性区影响较小。然而两种玻璃样品的远场应力分布区别十分明显,化学强化玻璃的远场Mises应力比原片玻璃更局限于表面压应力层深度范围内,而在水平方向上影响区域更广。远场Mises应力与材料弹性区域相关[19],化学强化玻璃远场Mises应力与原片玻璃的差异说明化学强化对玻璃的弹性区影响较大[22]。研究表明,当化学强化玻璃发生反向离子交换使得玻璃表面离子恢复原有状态时,玻璃的体积会完全恢复至离子交换前[22],说明化学强化的离子交换过程引入的应变是弹性应变。根据脆性材料压入理论,压痕过程可以分为3个明确的阶段:全弹性、弹塑性和全塑性。当压入载荷很小时,玻璃发生弹性变形,随着压入载荷的增大,逐渐由弹性变形转变为塑性变形。前期作者在研究化学强化铝硅酸盐玻璃在加载损伤过程的弹/塑性变形行为时,发现化学强化铝硅酸盐玻璃发生弹/塑性变形转变的临界载荷高于原片铝硅酸盐玻璃,同样证明化学强化玻璃能够在更大的载荷范围内发生弹性应变[3],这些研究成果与有限元模拟的结果是一致的。
3 结论(1) 采用Larsson塑性公式计算得出的玻璃屈服应力及塑性区域应力应变关系进行有限元模拟得到的压痕载荷-位移曲线与实验结果吻合度高,有限元方法能够准确模拟化学强化铝硅酸盐玻璃的纳米压痕实验过程。
(2) 压入深度相同时,化学强化铝硅酸盐玻璃相比原片铝硅酸盐玻璃的压入载荷较大,而接触面积较小。
(3) 根据有限元模拟得到的载荷-位移曲线,采用Oliver-Pharr方法计算得到的硬度值与实验得到的硬度值的相对误差为10%,杨氏模量的相对误差为2%,表明采用有限元方法能够较好地预测样品的硬度和杨氏模量。
(4) 有限元给出的Von Mises应力分布说明化学强化对铝硅酸盐玻璃的弹性区影响较大,对塑性区影响较小。
| [1] |
WANG M B, JIANG L B, LI X Y, et al. Structure and mechanical response of chemically strengthened aluminosilicate glass under different post-annealing conditions[J]. Journal of Non-Crystalline Solids, 2021, 554: 120620. DOI:10.1016/j.jnoncrysol.2020.120620 |
| [2] |
LI X Y, JIANG L B, MOHAGHEGHIAN I, et al. New insights into nanoindentation crack initiation in ion-exchanged sodium aluminosilicate glass[J]. Journal of the American Ceramic Society, 2018, 101: 2930-2940. DOI:10.1111/jace.15465 |
| [3] |
LI X Y, JIANG L B, MOHAGHEGHIAN I, et al. Elastic-plastic deformation in ion-exchanged aluminosilicate glass by loading rate dependent nanoindentation[J]. Journal of Non-Crystalline Solids, 2018, 491: 79-88. DOI:10.1016/j.jnoncrysol.2018.04.003 |
| [4] |
YOSHIDA S. Indentation deformation and cracking in oxide glass-toward understanding of crack nucleation[J]. Journal of Non-Crystalline Solids: X, 2019, 1: 100009-100017. DOI:10.1016/j.nocx.2019.100009 |
| [5] |
ANTUNES J M, FERNANDS J V, MENEZES L F, et al. A new approach for reverse analyses in depth-sensing indentation using numerical simulation[J]. Acta Materialia, 2007, 55(1): 69-81. DOI:10.1016/j.actamat.2006.08.019 |
| [6] |
SIMOES M I, MARIA J M, ANTUNES J V, et al. Numerical simulation of the depth-sensing indentation test with knoop indenter[J]. Metals, 2018, 8(11): 885-900. DOI:10.3390/met8110885 |
| [7] |
WEN W, BECKER A, SUN W. Determination of material properties of thin films and coatings using indentation tests: a review[J]. Journal of Materials Science, 2017, 52(21): 12553-12573. DOI:10.1007/s10853-017-1348-3 |
| [8] |
ANTUNES J M, FERNANDS J V, MENEZES L F, et al. A new approach for reverse analyses in depth-sensing indentation using numerical simulation[J]. Acta Materialia, 2007, 55(1): 69-81. DOI:10.1016/j.actamat.2006.08.019 |
| [9] |
YOFFE E. Elastic stress fields caused by indenting brittle materials[J]. Philosophical Magazine A, 1982, 46(4): 617-628. DOI:10.1080/01418618208236917 |
| [10] |
CHIANG S, MARSHALL D, EVANS A. The response of solids to elastic/plastic indentation Ⅰ stresses and residual stresses[J]. Journal of Applied Physics, 1982, 53(1): 298-311. DOI:10.1063/1.329930 |
| [11] |
LAURSEN T A, SIMO J C. A study of the mechanics of microindentation using finite elements[J]. Journal of Materials Research, 1992, 7(3): 618-626. DOI:10.1557/JMR.1992.0618 |
| [12] |
GIANNAKOPOULOS A E, LARSSON P L, VESTERGAARD R. Analysis of Vickers indentation[J]. International Journal of Solids & Structures, 1994, 31(19): 2679-2708. |
| [13] |
LARSSON P L, GIANNAKOPOULOS A E, SODERLUND E, et al. Analysis of Berkovich indentation[J]. International Journal of Solids & Structures, 1996, 33(2): 221-248. |
| [14] |
ZENG K, GIANNAKOPOULOS A E, ROWCLIFFE D J. Vickers indentations in glass-Ⅱ comparison of finite element analysis and experiments[J]. Acta Metallurgica et Materialia, 1995, 43(5): 1945-1954. DOI:10.1016/0956-7151(94)00393-V |
| [15] |
LI C S, LIANG C Z, LIN S, et al. A finite element study on the effects of densification on fused silica under indentation[J]. Ceramics International, 2020, 46(17): 26861-26870. DOI:10.1016/j.ceramint.2020.07.162 |
| [16] |
KANG M, LI M, LEONG A F T, et al. Crack nucleation and growth during dynamic indentation of chemically-strengthened glass[J]. Extreme Mechanics Letters, 2020, 38: 100754-100760. DOI:10.1016/j.eml.2020.100754 |
| [17] |
ZHANG W, SUBHASH G. An elastic-plastic-cracking model for finite element analysis of indentation cracking in brittle materials[J]. International Journal of Solids & Structures, 2001, 38(34): 5893-5913. |
| [18] |
LEE H, JIN H L, PHARR G M. A numerical approach to spherical indentation techniques for material property evaluation[J]. Journal of the Mechanics & Physics of Solids, 2013, 53(9): 2037-2069. |
| [19] |
BUCHHEIT T. Measuring residual stress in glasses and ceramics using instrumented indentation[J]. Journal of Materials Research, 2007, 22(10): 2875-2887. DOI:10.1557/JMR.2007.0358 |
| [20] |
BOLSHAKOV A, PHARR G. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques[J]. Journal of Materials Research, 1998, 13(4): 1049-1058. DOI:10.1557/JMR.1998.0146 |
| [21] |
JANNOTTI P, SUBHASH G, IFJU P, et al. Influence of ultra-high residual compressive stress on the static and dynamic indentation response of a chemically strengthened glass[J]. Journal of the European Ceramic Society, 2012, 32(8): 1551-1559. DOI:10.1016/j.jeurceramsoc.2012.01.002 |
| [22] |
TANDIA A, VARGHEESE K D, MAURO J C. Elasticity of ion stuffing in chemically strengthened glass[J]. Journal of Non-Crystalline Solids, 2012, 358(12): 1569-1574. |
 2021, Vol. 49
2021, Vol. 49


