文章信息
- 高玉魁
- GAO Yu-kui
- 负泊松比超材料和结构
- Auxetic metamaterials and structures
- 材料工程, 2021, 49(5): 38-47
- Journal of Materials Engineering, 2021, 49(5): 38-47.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000391
-
文章历史
- 收稿日期: 2019-04-27
- 修订日期: 2020-09-14
2. 上海市金属功能材料开发应用重点实验室, 上海 201804
2. Shanghai Key Laboratory of R&D for Metallic Function Materials, Shanghai 201804, China
自21世纪初以来,超材料已经逐渐发展成为新材料技术的一个重要分支。超材料是设计材料的内部结构,从而人为控制材料的各种属性以获得自然界没有的新材料。超材料因其声学、光学、热传导、吸能耗能等方面具有杰出的优势,在航空航天、生物医疗、能源动力、交通运输等方面发挥着至关重要的作用[1]。超材料的发展受到世界各国的重点关注,国家“十三五”规划纲要和《中国制造2025》中明确提出了加大对超材料的投入和研发[2]。
机械超材料是一种具有违反直觉力学性质的人造结构,其特殊的性能不是取决于材料本身的属性,而是源于对其单元结构进行创新设计[3]。机械超材料的性能一般与杨氏模量(E)、剪切模量(G)、体积模量(K)和泊松比(ν)密切相关,前三个常数与材料的硬度、刚度、压缩性能相关。由经典弹性理论可知,各向同性材料的力学性能参数可以由其中的任意两个参数进行表示[4],见式(1)~(4)。
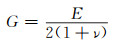
|
(1) |
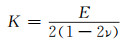
|
(2) |

|
(3) |

|
(4) |
泊松比(ν)定义为在弹性加载方向上材料的横向应变(εx)与纵向应变(εy)的比值的负数,即ν=-εx/εy。材料的弹性模量(E)和剪切模量(G)与泊松比(ν)密切相关[2]。当泊松比由正数变成负数时,材料的抗剪切能力显著提高。自从1987年Lakes[5]在Science提出了负泊松比超材料作为一种可设计材料的概念,负泊松比超材料和结构发展迅速,并在许多领域有广阔的应用前景。
本文从负泊松比超材料和结构的变形机理出发,综述了内凹结构、旋转刚体结构、手性/反手性结构、纤维/节点结构、折纸结构、褶皱结构、弯曲-诱导结构等物理模型,并对负泊松比超材料和结构未来的挑战和发展趋势进行了展望,以期为负泊松比超材料和结构的推广应用提供参考。
1 负泊松比超材料机理与结构 1.1 负泊松比超材料机理与力学性能大多数工程材料具有正泊松比,负泊松比超材料在受到轴向拉伸(或压缩)时,其垂直方向有膨胀(或收缩)的力学特性,也叫作拉胀材料(auxetic materials)。利用此特性可以设计出兼具舒适性与支撑性的鞋子、弹性座椅、护具等[6]。负泊松比效应使这种材料的力学性能得到增强,包括抗冲击性能、抗断裂性能、吸能隔振、渗透率可变性能、曲面同向性等[7]。
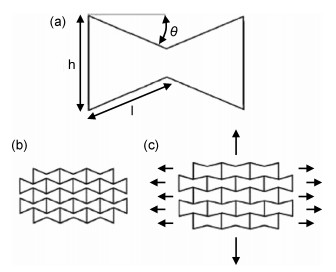
大多数工程材料(正泊松比材料)在受到冲击载荷时,垂直的冲击载荷会使材料向四周分离,如图 1(a)所示[8]。负泊松比超材料则正好相反,材料的竖向发生收缩的同时横向也会收缩,使材料向受冲击区域聚集密度瞬间增大,因此具有较好的抗冲击载荷的性能,如图 1(b)所示[8]。由经典弹性理论可知,材料的压痕阻力与硬度(H)密切相关,它与泊松比的关系如式(5)所示:

|
(5) |
式中:γ为敏感性指数,均布载荷时γ为1,集中载荷下为2/3。材料的压痕阻力现象随着负泊松比绝对值的增加而愈加明显[9]。负泊松比超材料的压痕阻力特性已经在防弹装备、聚合物、金属泡沫、纤维增强复合材料得到广泛的应用。
Choi等[10]研究发现负泊松比泡沫比传统泡沫具有较好的抗断裂性能。由于其断裂韧度受体积压缩率的影响,随着体积压缩率的增大其韧性也增大。Donoghue等[11]发现,负泊松比层压板材料比传统层压板材料裂纹的扩展需要更多能量,且具有更小的缺口敏感性,这也就意味着负泊松比超材料具有更强的抵抗裂纹的能力。
负泊松比超材料在吸能隔振方面展现了独特的优势。负泊松比泡沫因其独特的内部结构和独有的变形特性比传统泡沫更能吸能隔振,且取决于其孔的尺寸大小[12]。张梗林等[13]设计了一种新型宏观负泊松比蜂窝夹芯船舶隔振基座并分析了它的隔振性能。张相闻等[14-15]提出了具有正、负泊松比效应的新型船用抗冲击与低频隔振性能优异的蜂窝基座,并验证了该基座系统轻质和优良的隔振性能。
负泊松比超材料因其独特的多孔结构具有杰出的渗透率可变性能。当负泊松比超材料受到拉伸后孔隙在垂直方向上变宽,在横向和垂直方向上孔径变大[16]。由于负泊松比效应,这种渗透率可变性可以从宏观材料拓展到纳米材料,利用其孔洞尺寸随外力作用发生变化的特性可以用来制造过滤器、智能医药绷带。
当材料受到平面外弯矩时,会产生横向曲率。正泊松比材料会发生马鞍形的变形,其横向曲率与弯曲主曲率相反,如图 2(a)所示[17]。而负泊松比超材料横向曲率与主曲率方向一致,会发生拱形变形,也称为双曲率或同向曲率,如图 2(b)所示[17]。若发生拱形变形可以有效地减轻纯弯作用下的板或者梁的损伤,这种特性在飞机的机翼面板、整流罩及医疗领域也具有广泛的应用前景。
负泊松比超材料在自然界中早就出现,例如黄铁矿单晶体、α-方石英、沸石、硅酸盐、砷、镉以及生物材料中的多孔的松质骨骼、猫皮肤、奶牛乳头部分皮肤等[18]。由于在自然界中只有有限数量的负泊松比超材料可供使用,因此研究人员在开发具有负泊松比超材料性能的人工材料和结构方面作出了巨大的努力。一是通过对正泊松比材料的结构以及合理铺设方式获得负泊松比效应;二是通过创新材料的构筑方法和技术直接制备负泊松比超材料[19-21]。可控的变形机理产生的负泊松比行为并且易于制造已经成为研究的热点。典型的变形机理可以分为内凹结构[22-23]、旋转刚体结构[24]、手性/反手性结构[25-26]、纤维/节点结构[27]、折纸结构[28]、褶皱结构[29]、屈服-诱导结构[30]以及其他结构。
1.2.1 内凹结构常见的负泊松比超材料类型是内凹结构,它们是由薄肋和连接铰链组成的桁架结构构成的,如图 3(a)所示[9, 17]。图 3(b)[9, 17]为二维内凹六边形蜂窝结构,对其施加水平方向的单轴拉力,其h杆会向外移动,原因是l杆在受到水平方向的拉力时,内凹角θ展开,同时l杆发生旋转,整体机构膨胀产生负泊松比效应,如图 3(c)所示[9, 17]。
这种二维内凹六边形蜂窝结构的负泊松比效应主要取决于h杆、l杆的杆长、内凹角θ以及杆的厚度。随着对内凹结构的不断深入研究,对结构进行拓扑优化可以得到二维内凹三角形结构。这种结构的负泊松比效应主要取决于杆长和两杆之间的角度[31]。
星形胞元结构可以看作是由二维内凹蜂窝结构拓扑优化而得到。内凹星型结构是由3,4,6阶星型单元和连接每个单元的肋杆组成。不同星型单元分别具有3,4,6个方向的各向同性,4阶和6阶星型结构比3阶负泊松比效应更加明显,负泊松比的大小受连接杆刚度的影响,改变刚度对不同的星型结构性能的影响也不一样[32]。
三维内凹结构是由二维内凹结构基元转化设计而来,将二维内凹结构经过阵列、旋转、反转等方式镜像到三维内凹结构的方法可以设计出很多新型的三维内凹结构[33]。这种模式产生的结构有其优点也有缺点。该结构不仅具有一定的抗拉强度,而且对荷载也具有一定的抗压作用。因此,与仅在荷载的方向上具有负泊松比的效应的结构相比,这种结构具有广泛的适用性。而且,内凹结构具有高孔隙度或低密度,从轻质建筑的角度来看是有广泛应用的。然而,内凹结构是由复杂的薄肋连接而成的,这使得它们难以制造出高精度、无缺陷的内凹结构。以三维内凹结构为例,由于内部孔洞结构复杂,需要采用先进的增材制造技术。此外,解决薄肋的挠曲变形和剪切变形也是实现预期负泊松比效应的一个难题。当较大的压缩载荷施加于内凹结构时,薄肋可能发生动态模型中未考虑的屈曲现象。此外,薄肋容易发生疲劳失效,可能导致整体结构的耐久性降低。内凹结构主要应用于轻质夹层板的核心结构和分析模型中,用于研究负泊松比泡沫的微观结构。
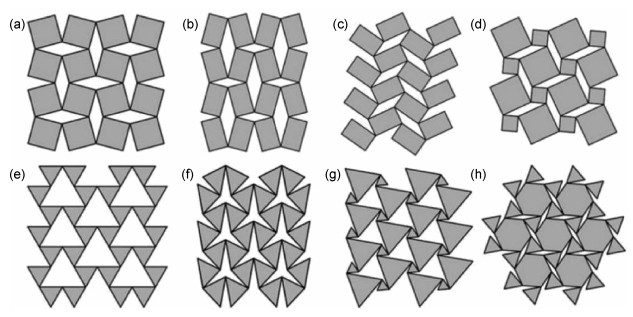
1.2.2 旋转刚体结构另一种具有代表性的负泊松比结构是旋转刚体结构。旋转刚体结构是由柔性铰链连接的刚性单元组成。刚性单元按照一定的规则排列,其初始位置以顺时针方向或逆时针方向轻微倾斜,与附近单元的倾斜方向相反。具有这种结构模型的一个典型例子是旋转正方形单元结构。正方形刚性单元按一定规律沿纵向和横向排列。四个正方形刚体单元在初始位置有轻微倾斜,并形成菱形空隙,如图 4(a)所示[34]。正方形刚体单元的初始倾斜引起相对于拉伸载荷的旋转,并直接影响横向变形。由于正方形单元的初始倾斜位置,所施加的拉伸载荷在上下铰链之间并不是共线的。当受到拉力时,扭矩将施加到正方形单元体上,单元体以顺时针方向或逆时针方向旋转,与其相邻单元体运动方向相反。由于单元体是刚性的,与铰链相比几乎不变形,单元体的局部旋转会导致侧边铰链的横向运动和侧向扩展。局部的旋转产生了负泊松比效应。旋转正方单元结构是最简单的二维结构,可以用来构造各种二维单元结构,例如,矩形结构、平行四边形结构、反矩形结构和双方单元结构,如图 4(b)~(d)所示[34]。与四边形相似,等边三角形单元也是最简单的单元,具有任意三角形或非均匀三角形的旋转单元结构是由其发展而来,如图 4(e)~(h)所示[34]。然而,由于单元是刚性的,它们不会发生明显的变形,大多数变形发生铰链弯曲。这种变形引起铰链区域的应力集中,使结构的耐久性变差。另外,由于孔隙率较低,给工程结构件减重带来了困难。
一种具有单位圆和肋杆的手性基元(物体镜像后不能与本体重合)也会引起负泊松比行为[35]。手性结构的单位圆规则地排列在三、四、六边形上,肋杆和单位圆相切,两个单位圆通过一个肋杆相连。当法向载荷施加于阵列排列的手性结构时,载荷通过肋杆转移到单位圆上,产生绕圆心的转动力矩。该单位圆然后向某一方向旋转,并通过与负载不同方向连接的肋杆拉或推相邻的单位圆。二维手性结构是由单位圆和肋杆组成的,与其他类型的无限制变化的负泊松比结构不同。根据单位圆排列规律,手性结构主要分为三切向、四切向和六切向结构,根据单位圆的旋转方向被划分为手性结构和反手性结构。
Chan等[36]研究具有负泊松比的三维手性各向同性晶格发现,三维手性晶格由刚性立方体节点和多个肋杆组成。泊松比与晶格的几何形状相关,可以调控到负值。随着晶格单元的增加,泊松比由正向负递减,晶格易受到尺寸效应的影响。
1.2.4 纤维/节点结构纤维/节点结构是由传递拉伸载荷的纤维和刚性节点单元组成。纤维连接到节点,如果没有作用力,节点与纤维交织在一起。然而,当拉伸载荷施加于纤维/节点结构时,拉伸载荷会使纤维伸直。在此过程中,纤维向垂直载荷方向推拉节点,增加与相邻纤维和节点的距离。纤维上的拉伸力使纤维发生膨胀,从而产生负泊松比效应[37]。根据纤维和节点的连接方式,纤维/节点结构大致分为两种类型:束型和网状结构。如图 5(a)所示[38],束状纤维/节点结构由单纤维/节点链组成。每条单链都有一个各向异性的节点连在一排的纤维上。当纤维被拉伸时,纤维与结节交织在一起,从而增加纤维/节点链的有效半径。这导致单链相互推动,整个束型结构在垂直方向施加载荷间接扩展。网络型的纤维/节点结构其中一个节点连接多个纤维,是一个连接纤维的网络节点,如图 5(b),(c)所示[38]。当网状纤维/节点结构施加拉伸载荷时,相互缠绕的纤维在节点之间展开。拉伸载荷直接导致纤维/节点结构在各方向产生膨胀,从而引起负泊松比效应。
三浦折纸(Miura origami)具有周期性、可展开性等特点,可应用于空间展开结构-太阳能帆板中。Miura折纸结构的面内和离面泊松比大小相等,符号相反且与材料的性质无关。Lv等[39]研究发现Miura型折叠机械超材料的尺寸往往是有限的,并不是折叠基本单元的理想周期分布,因此需要考虑边界效应。通过调整平行四边形网格的角度、底部形状和结构的高度,可以调节材料的力学性能。折纸结构不需要使用增材制造技术,操作简单。因该结构存在折叠线,导致该结构比其负泊松比超材料结构的刚性要小,耐久性低,且存在应力集中。
褶皱结构内部为随机和各向同性的结构单元。压缩或化学缺陷会使材料中产生微观的皱褶,去除褶皱会产生负泊松比效应[40]。因此当拉伸载荷施加在皱缩的结构上时,皱褶会向各个方向展开和膨胀。与其他负泊松比效应机制不同,皱缩结构可以应用于处理流体的工程问题,如流体输送。与制造过程中要求高精度的其他结构相比,这使得获得高质量的负泊松比超材料变得容易。此外,通过压缩褶皱结构和控制其中的缺陷,可以有效地控制整个材料的力学性能。
1.2.6 弯曲-诱导、螺旋纱线和其他结构弯曲-诱导结构是一种特殊的结构,负泊松比效应是由弯曲产生的,弯曲-诱导结构材料只有在施加的压缩力大于临界值时才具有负泊松比效应。此外,具有弯曲-诱导结构的负泊松比超材料在初始形状或小应变范围内不表现出负泊松比效应。弯曲-诱导结构是用简单的圆形图案在竖直和水平方向上按一定规则间隔排列在二维薄板上,如图 6(a)所示[41]。由于受压载荷和应变大小的影响,弯曲-诱导结构表现出特性不同。在较小的应变范围内,由于放置圆的对称性,由弯曲引起的负泊松比效应经历了与传统结构相似的线弹性变形。在线性变形阶段,或预弯曲阶段,没有出现较大的横向变形。然而,随着载荷的增加超过临界应变点,它会向弯曲阶段转移,从而出现非线性变形。在施加的压缩载荷作用下,圆形图案之间薄弱部分被对称地弯曲和变形。圆形图案呈椭圆形或哑铃状,在纵向和横向交替。在这一过程中,整个结构不仅在压缩载荷方向上收缩,而且在侧向方向上也在收缩,从而导致了负泊松比行为。在后屈曲阶段,载荷进一步增加,负泊松比效应保持不变。在这个阶段,结构不再像线性变形阶段那样具有负泊松比效应。弯曲-诱导结构的机理可以较容易地从2D圆形图案片材转换到3D结构中,如图 6(b), (c)所示[42]。
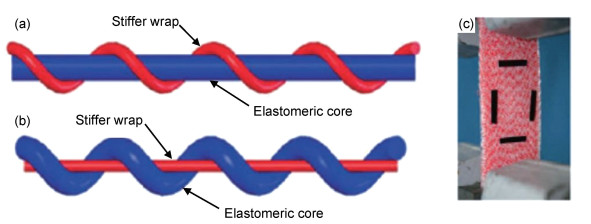
螺旋纱线是一种独特的负泊松比结构,它由两种类型纱线组成。其中一种芯部纱线弹性模量较小,在无应力状态下呈直线形。另一种包缠纱线的弹性模量较大,但有很高的刚度。包缠纱线螺旋缠绕紧贴在芯部纱线上,两个纱线之间不存在相对移动。在初始状态下,整个螺旋负泊松比纱线的有效直径定义为芯部纱线的直径加上包裹纱线直径的两倍,如图 7(a)所示[43]。当拉伸载荷施加在螺旋纱线上时,由于两个纱线之间刚度值的差异,形状会发生巨大的变化。由于包裹纱线比芯部纱线弹性模量大伸长量较小,螺旋缠绕的纱线在拉伸载荷方向上被拉直,伸长量较大的芯部纱线被包缠纱线压弯,并沿着包缠纱线螺旋缠绕,两种纱线的位置发生了互换,如图 7(b)所示[43]。因此,在无应力状态下,整体纱线的有效直径为包裹纱线的直径加上芯部纱线直径的两倍。由于芯部纱线直径比缠绕包缠纱线直径大,整体纱线有效直径因受拉伸而增大。因此,螺旋纱线组成的整个织物具有负泊松比效应,如图 7(c)所示[43]。不同于其他负泊松比结构,螺旋负泊松比纱线的优点是可以很容易地将自由形状的表面(如人体)包围起来。然而,这种结构由没有抗剪能力的芯部纱线和包缠纱线组成,因此在受压荷载作用下,相对于其他结构它们并不能表现出优异的负泊松比性能。
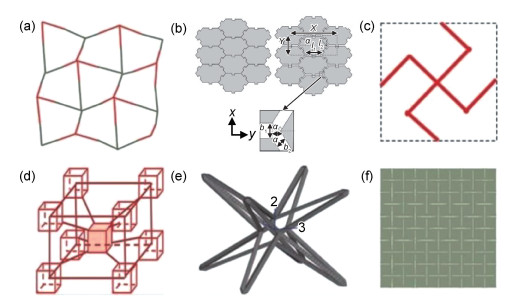
鸡蛋架结构(egg rack structure)主要由四爪结构构成,如图 8(a)所示[44]。四爪结构受横向拉力展开,从而发生负泊松比效应[44]。联锁六边形模型由多个六边形刚体组成,相邻两刚体互相扣接,形成锁结。当结构受拉伸时,会产生负泊松比效应,如图 8(b)所示[45]。图 8(c)为一种新型交错肋结构,研究发现交错肋结构适用于预测聚氨酯泡沫的泊松比和应力-应变关系[46]。图 8(d)为三维节点连杆结构[47],由四方节点组成的周期性结构,通过杆状单元互相连接,通过连杆的弯曲来实现负泊松比效应,可以用来解释e-PTFE、e-UHMWPE、e-PA、体心立方金属和泡沫的负泊松比行为。图 8(e)为一种六面体结构,具有优异的压陷阻力,可用作结构件[48]。图 8(f)为穿孔板结构,该结构可以模拟出内凹结构、旋转刚体结构、手性/反手性结合及纤维-节点结构的变形机制[49-50]。
|
图 8 其他负泊松比超材料结构[44-50] (a)四爪结构;(b)联锁六边形模型;(c)交错肋结构;(d)三维节连杆结构;(e)六面体结构;(f)穿孔板结构 Fig. 8 Other auxetic metamaterial structure[44-50] (a)four claw structure; (b)interlocking hexagon model; (c)staggered rib structure; (d)three-dimensional link structure; (e)hexahedral structure; (f)perforated plate construction |
负泊松比超材料独特的结构和性能,使其在许多领域具有潜在广泛的应用,如表 1所示[8, 13-14, 48, 51-59]。立方金属中负泊松比效应的存在具有重要的意义,尤其是负泊松比逆转了正泊松比对单轴应力引起的体积和面积变化的补偿效应。最小泊松系数为-0.18的单晶Ni3Al可以用来制作燃气涡轮发动机的叶片,因其优异的抗冲击性能可以应用于飞机机翼、机身[51]。负泊松比浮筏结构具有隔振效果好、降噪性能强、质量轻等优点,在航海船舶动力设备舱室减振中具有重要的应用[13-14]。基于形状记忆合金混合蜂窝桁架的深空天线,可展开特性通过蜂窝结构的负泊松比行为得到增强[53]。双箭头型负泊松比结构的新型吸能盒在汽车碰撞过程中可以通过变形吸能,从而减轻碰撞,对乘客起到一定的保护作用[56]。采用负泊松比超材料制作的汽车安全带、汽车缓冲垫、头盔、座椅等,比传统材料更加安全舒适[54]。在生物医疗方面,负泊松比超材料可以用于制造医用绷带、人造皮肤、血管支架、脉搏监测器等医疗设备。采用负泊松比胞元结构的设计可以很好地解决传统血管支架径向膨胀撑开血管的同时轴向缩短的难题。既有效保护了血管壁,也保证了支架的准确定位[8]。在军事国防方面,负泊松比超材料可以用来制作防弹背心、作战服、头盔等[58]。在纺织工业,负泊松比超材料可以用来制作纱线、保暖内衣、鞋、孕妇服等[59]。
| Field | Application | Reference |
| Aerospace industry, navigation | Jet engine turbine blade, aerocraft wing, rocket fuselage, ship, antenna | [13-14, 51-53] |
| Mechanical automation | Vehicle bumpers and seat cushions, adapting piece, safety belt, sensors, heatset, tyre, crash box | [48, 54-56] |
| Biomedical | Bandage, dental floss, artificial blood vessel, artificial skin, esophagus and stents, heart valve ring, pulse monitor | [8, 57] |
| Military science | Helmet, bulletproof vest, combat dress, silencer, bullet | [58] |
| Textile industry | Yarn, fiber, texture, kneecap, gloves, shoes, thermal underwear | [59] |
近年来负泊松比超材料和结构发展十分迅速。大量的负泊松比超材料和结构被发现、制造和研究,其中包含金属、复合材料、纤维、纱线、泡沫、陶瓷等。但负泊松比超材料和结构实际应用仍然处于初级阶段,未来的工作重点是发展具有实际工程应用的负泊松比超材料。应该考虑负泊松比效应与其他超材料性能的结合,如形状记忆和电磁效应,以制作多功能的负泊松比超材料和结构,提升材料的性能和扩大材料的应用范围。航空航天和航海、生物医疗、军事等领域的实际应用是负泊松比超材料和结构未来发展的一个趋势。其次,将负泊松比超材料和结构与常规材料相结合将扩大仅通过负泊松比效应或者使用常规材料未达到力学性能的设计空间。此外,不同材料或者不同技术制造同样的负泊松比结构表现出不同的力学性能也需要进行深入研究。
3 结束语基于前述关于负泊松比超材料的分析结果,本文可得到如下结论:
(1) 负泊松比超材料有着优异的抗剪切性能、抗断裂性能、抗冲击隔振性能、消音吸能性能、渗透率可变性能、曲面同向性能等。但是,大多数负泊松比结构都有铰链和孔隙,而且由于其几何形状和变形机制的特点,这些结构往往比传统的实体材料刚度、硬度要低。因此,负泊松比超材料在大型承重结构中的使用是有限的。此外,在铰链区域附近会产生应力集中,使负泊松比结构材料易受循环疲劳荷载的影响。因此,在设计和使用负泊松比结构材料时,必须特别注意考虑负泊松比效应对材料性能弱化的影响。
(2) 本文基于材料力学,即3个弹性模量与泊松比之间的关系,对负泊松比超材料原理及结构进行了总结,从原理-结构-应用关系的角度出发,综述了负泊松比超材料最新的研究进展及应用,其中结构包括:内凹结构、旋转刚体结构、手性/反手性结构、纤维/节点结构、折纸结构、褶皱结构、弯曲-诱导结构等。
(3) 不同的增材制造技术制备负泊松比超材料可以增加制造柔性,减小尺寸的晶粒,扩大负泊松比超材料的使用范围。但是如何降低增材制造的成本是实现负泊松比结构材料广泛应用的一个难题。其次,负泊松比超材料是通过人工结构设计来调节材料的力学性能,需要尽可能地缩小结构的尺寸,负泊松比超材料就越接近材料本身的性质。新型高精度高分辨率的微纳加工技术与测量技术的深入研究对负泊松比超材料的发展起着至关重要的作用。采用拓扑结构优化方法和有限元仿真模拟来设计具有优异性能的负泊松比超材料将是未来发展的一个重要趋势。将负泊松比结构材料与智能材料相结合可以使材料本身具备感知外界环境变化的能力,并且做出相应的响应。因此,关于负泊松比超材料和结构的理论研究与应用有待进一步深入探索。
| [1] |
YU X L, ZHOU J, LIANG H Y, et al. Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review[J]. Progress in Materials Science, 2018, 94: 114-173. DOI:10.1016/j.pmatsci.2017.12.003 |
| [2] |
于靖军, 谢岩, 裴旭. 负泊松比超材料研究进展[J]. 机械工程学报, 2018, 54(13): 1-14. YU J J, XIE Y, PEI X. State-of-art of metamaterials with negative Poisson's ratio[J]. Journal of Mechanical Engineering, 2018, 54(13): 1-14. |
| [3] |
杨智春, 邓庆田. 负泊松比材料与结构的力学性能研究及应用[J]. 力学进展, 2011(3): 335-350. YANG Z C, DENG Q T. Mechanical property and application of materials and structures with nagative Possion's ratio[J]. Advances in Mechanics, 2011(3): 335-350. |
| [4] |
YANG W, LI Z M, SHI W, et al. Review on auxetic materials[J]. Journal of Materials Science, 2004, 39: 3269-3279. DOI:10.1023/B:JMSC.0000026928.93231.e0 |
| [5] |
LAKES R. Foam structures with a negative Poisson's ratio[J]. Science, 1987, 235: 1038-1040. DOI:10.1126/science.235.4792.1038 |
| [6] |
NOVAK N, VESENJAK M, REN Z. Auxetic cellular materials-a review[J]. Journal of Mechanical Engineering, 2016(9): 485-493. |
| [7] |
HVEONHO C, DONGSIK S, KIM D N. Mechanics of auxetic materials. handbook of mechanics of materials[M]. Singapore: Springer, 2018: 1-25.
|
| [8] |
任鑫, 张相玉, 谢亿民. 负泊松比材料和结构的研究进展[J]. 力学学报, 2019, 51(3): 656-689. REN X, ZHANG X Y, XIE Y M. Research progress in auxetic materials and structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 656-689. |
| [9] |
KOLKEN H M A, ZADPOOR A A. Auxetic mechanical metamaterials[J]. RSC Advances, 2017, 7: 5111-5129. DOI:10.1039/C6RA27333E |
| [10] |
CHOI J B, LAKES R S. Non-linear properties of metallic cellular materialswith a negative Poisson's ratio[J]. Journal of Materials Science, 1992, 27(19): 5375-5381. DOI:10.1007/BF02403846 |
| [11] |
DONOGHUE J P, ALDERSON K L, EVANS K E. The fracture toughness of composite laminates with a negative Poisson's ratio[J]. Physica Status Solidi (B), 2009, 246(9): 2011-2017. DOI:10.1002/pssb.200982031 |
| [12] |
CHEKKAL I, BIANCHI M, REMILLAT C, et al. Vibro-acoustic properties of auxetic open cell foam: model and experimental results[J]. Acta Acustica United Acustica, 2010, 96: 266-274. DOI:10.3813/AAA.918276 |
| [13] |
张梗林, 杨德庆. 船舶宏观负泊松比蜂窝夹芯隔振器优化设计[J]. 振动与冲击, 2013, 32(22): 68-72. ZHANG G L, YANG D Q. Optimization design of an auxetic honeycomb isolator in a ship[J]. Journal of Vibration and Shock, 2013, 32(22): 68-72. DOI:10.3969/j.issn.1000-3835.2013.22.013 |
| [14] |
张相闻, 杨德庆. 船用新型抗冲击隔振蜂窝基座[J]. 振动与冲击, 2015, 34(10): 40-45. ZHANG X W, YANG D Q. A novel marine impact resistance and vibration isolation cellular base[J]. Journal of Vibration and Shock, 2015, 34(10): 40-45. |
| [15] |
ZHANG X W, YANG D Q. Numerical and experimental studies of a light-weight auxetic cellular vibration isolation base[J]. Shock and Vibration, 2016, 9: 1-16. |
| [16] |
WANG Z Y, HU H. Auxetic materials and their potential applications in textiles[J]. Textile Research Journal, 2014, 84(15): 1600-1611. DOI:10.1177/0040517512449051 |
| [17] |
EVANS K E, ALDERSON A. Auxetic materials: functional materials and structures from lateral thinking[J]. Advanced Materials, 2000, 12: 617-628. DOI:10.1002/(SICI)1521-4095(200005)12:9<617::AID-ADMA617>3.0.CO;2-3 |
| [18] |
CARNEIRO V H, MEIRELES J, PUGA H. Auxetic materials-a review[J]. Materials Science-Poland, 2013, 31(4): 561-571. DOI:10.2478/s13536-013-0140-6 |
| [19] |
CRESPO J, FRANCISCO J M. A continuum approach for the large strain finite element analysis of auxetic materials[J]. International Journal of Mechanical Sciences, 2018, 135: 441-457. DOI:10.1016/j.ijmecsci.2017.11.038 |
| [20] |
YANG L, HARRYSSON O, WEST H, et al. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing[J]. International Journal of Solids and Structures, 2015, 69/70: 475-490. DOI:10.1016/j.ijsolstr.2015.05.005 |
| [21] |
CARNEIRO V H, PUGA H. Axisymmetric auxetics[J]. Composite Structures, 2018, 195: 232-248. DOI:10.1016/j.compstruct.2018.04.058 |
| [22] |
HU L L, LUO Z R, ZHANG Z Y, et al. Mechanical property of re-entrant anti-trichiral honeycombs under large deformation[J]. Composites: Part B, 2019, 163: 107-120. DOI:10.1016/j.compositesb.2018.11.010 |
| [23] |
WANG H, LU Z X, YANG Z Y, et al. A novel re-entrant auxetic honeycomb with enhanced in-plane impact resistance[J]. Composite Structures, 2019, 8: 758-770. |
| [24] |
KIM J, SHIN D, YOO D S, et al. Regularly configured structures with polygonal prisms for three-dimensional auxetic behavior[J]. Proceedings of the Royal Society A, 2017, 473(2202): 20160926. DOI:10.1098/rspa.2016.0926 |
| [25] |
LAKES R. Deformation mechanisms in negative Poisson's ratio materials: structural aspects[J]. Journal of Materials Science, 1991, 26(9): 2287-2292. DOI:10.1007/BF01130170 |
| [26] |
GRIMA J N, GATT R, FARRUGIA P S, et al. On the properties of auxetic meta-tetrachiral structures[J]. Physica Status Solidi (b), 2008, 245(3): 511-520. DOI:10.1002/pssb.200777704 |
| [27] |
ALDERSON A, EVANS K E. Modelling concurrent deformation mechanisms in auxetic microporous polymers[J]. Journal of Materials Science, 1997, 32(11): 2797-2809. DOI:10.1023/A:1018660130501 |
| [28] |
MAHADEVAN L, RICA S. Self-organized origami[J]. Science, 2005, 307: 1740. DOI:10.1126/science.1105169 |
| [29] |
LAKES R. Deformation mechanisms in negative Poisson's ratio materials: structural aspects[J]. Journal of Materials Science, 1991, 26(9): 2287-2292. DOI:10.1007/BF01130170 |
| [30] |
JAVID F, LIU J, SHIM J, et al. Mechanics of instability-induced pattern transformations in elastomeric porous cylinders[J]. Journal of the Mechanics and Physics of Solids, 2016, 96: 1-17. DOI:10.1016/j.jmps.2016.06.015 |
| [31] |
SAXENA K K, DAS R, CALIUS E P. Three decades of auxetics research-materials with negative Poisson's ratio: a review[J]. Advanced Engineering Materials, 2016, 18(11): 1847-1870. DOI:10.1002/adem.201600053 |
| [32] |
GRIMA J N, GATT R, ALDERSON A. On the potential of connected stars as auxetic systems[J]. Molecular Simulation, 2005, 13: 923-934. |
| [33] |
LI Y, OLA H, HARVEY W, et al. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing[J]. International Journal of Solids and Structures, 2015, 69/70: 475-490. DOI:10.1016/j.ijsolstr.2015.05.005 |
| [34] |
GRIMA J N, GATT R, ALDERSON A, et al. On the auxetic properties of rotating rectangles' with different connectivity[J]. Journal of the Physical Society of Japan, 2005, 74: 2866-2867. DOI:10.1143/JPSJ.74.2866 |
| [35] |
ALSERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science and Technology, 2010, 70: 1042-1048. DOI:10.1016/j.compscitech.2009.07.009 |
| [36] |
CHAN S H, MICHAEL E. P, RODERIC S L. Chiral three-dimensional isotropic lattices with negative Poisson's ratio[J]. Physics Status Solidi B, 2016, 253(7): 1243-125. DOI:10.1002/pssb.201600055 |
| [37] |
EVANS K E, CADDOCK B D. Microporous materials with negative Poisson's ratios Ⅱ. mechanismsand interpretation[J]. Journal of Physics D, 1989, 22: 1877-1883. DOI:10.1088/0022-3727/22/12/012 |
| [38] |
HE C, LIU P, GRIFFIN A C. Toward negative Poisson ratio polymers through molecular design[J]. Macromolecules, 1998, 31: 3145-3147. DOI:10.1021/ma970787m |
| [39] |
LV C, KRISHNARAJU D, KONJEVOD G, et al. Origami based mechanical metamaterials[J]. Scientific Reports, 2014, 4: 5979. |
| [40] |
BOUAZIZ O, MASSE J P, ALLAIN S, et al. Compression of crumpled aluminum thin foils and comparison with other cellular materials[J]. Materials Science and Engineering: A, 2013, 570: 1-17. DOI:10.1016/j.msea.2013.01.031 |
| [41] |
BERTOLDI K, BOYCE M C, DESCHANEL S, et al. Mechanics of deformation-triggered pattern transformations and superelastic behavior in periodic elastomeric structures[J]. Journal of the Mechanics and Physics of Solids, 2008, 56: 2642-2668. DOI:10.1016/j.jmps.2008.03.006 |
| [42] |
SHIM J, PERDIGOU C, CHEN E R, et al. Buckling-induced encapsulation of structured elastic shells under pressure[J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109: 5978-5983. DOI:10.1073/pnas.1115674109 |
| [43] |
MILLER W, HOOK P B, SMITH C W, et al. The manufacture and characterisation of a novel, low modulus, negative Poisson's ratio composite[J]. Composite Science Technology, 2009, 69: 651-655. DOI:10.1016/j.compscitech.2008.12.016 |
| [44] |
GRIMA J N, RAVIRALA, GALEA R, et al. Modelling and testing of a foldable macrostructure exhibiting auxetic behaviour[J]. Physica Status Solidi (b), 2011, 248(1): 117-122. DOI:10.1002/pssb.201083982 |
| [45] |
RAVIRALA N, ALDERSON A, ALDERSON K L. Interlocking hexagons model for auxetic behaviour[J]. Journal of Materials Science, 2007, 42(17): 7433-7445. DOI:10.1007/s10853-007-1583-0 |
| [46] |
SMITH C W, GRIMA J N, EVANS K E. A novel mechanism for generating auxetic behaviour in reticulated foams: missing rib foam model[J]. Acta Materialia, 2000, 48(17): 4349-4356. DOI:10.1016/S1359-6454(00)00269-X |
| [47] |
GASPAR N, SMITH C W, ALDERSON A, et al. A generalised three-dimensional tethered-nodule model for auxetic materials[J]. Journal of Materials Science, 2011, 46(2): 372-384. DOI:10.1007/s10853-010-4846-0 |
| [48] |
DIRRENBERGER J, FOREST S, JEULIN D. Effective elastic properties of auxetic microstructures: anisotropy and structural applications[J]. International Journal of Mechanics and Materials in Design, 2013, 9(1): 21-33. DOI:10.1007/s10999-012-9192-8 |
| [49] |
GRIMA J N, GATT R. Perforated sheets exhibiting negative Poisson's ratios[J]. Advanced Engineering Materials, 2010, 12(6): 460-464. DOI:10.1002/adem.201000005 |
| [50] |
MIZZI L, AZZOPARDI K M, ATTARD D, et al. Auxetic metamaterials exhibiting giant negative Poisson's ratios[J]. Physica Status Solidi-rapid Research Letters, 2015, 9(7): 425-430. DOI:10.1002/pssr.201510178 |
| [51] |
BAUGHMAN R H, SHACKLETTE J M, ZAKHIDOV A A, et al. Negative Poisson's ratios as a common feature of cubic metals[J]. Nature, 1998, 392: 362-365. DOI:10.1038/32842 |
| [52] |
颜芳芳, 徐晓东. 负泊松比柔性蜂窝结构在变体机翼中的应用[J]. 中国机械工程, 2012(5): 542-546. YAN F F, XU X D. Negative Poisson's ratio honeycomb structure and its applications in structure design of morphing aircraft[J]. China Mechanical Engineering, 2012(5): 542-546. DOI:10.3969/j.issn.1004-132X.2012.05.007 |
| [53] |
JACOBS S, COCONNIER C, DIMIAIO D, et al. Deployable auxetic shape memory alloy cellular antenna demonstrator: design, manufacturing and modal testing[J]. Smart Materials and Structures, 2012, 21(7): 075013. DOI:10.1088/0964-1726/21/7/075013 |
| [54] |
亓昌, 安文姿, 杨姝. 负泊松比安全带织带乘员碰撞保护性能的FE仿真[J]. 汽车安全与节能学报, 2013, 4(3): 215-222. QI C, AN W Z, YANG S. FE simulation of the occupant crash protection performance of the negative Poisson's ratio seat belt webbing[J]. Journal of Automotive Safety and Energy, 2013, 4(3): 215-222. DOI:10.3969/j.issn.1674-8484.2013.03.003 |
| [55] |
AVELLANEDA M, SWART P J. Calculating the performance of 1-3 piezocomposites for hydrophone applications: an effective medium approach[J]. Journal of the Acoustica1 Society of America, 1998, 103: 1449-1467. DOI:10.1121/1.421306 |
| [56] |
ZHOU G, MA Z D, LI G Y, et al. Design optimization of a novel NPR crash box based on multi-objective genetic algorithm[J]. Struct Multidisc Optim, 2016, 54: 673-684. DOI:10.1007/s00158-016-1452-z |
| [57] |
马丕波, 常玉萍, 蒋高明. 负泊松比针织结构及其应用[J]. 纺织导报, 2015, 7: 47-50. MA P B, CHANG Y P, JIANG G M. Knitted structures with negative Poisson's ratio[J]. China Textile Leader, 2015, 7: 47-50. |
| [58] |
SAXENA K K, DAS R, CALIUS E P. Three decades of auxetics research-materials with negative Poisson's ratio: a review[J]. Advanced Engineering Materials, 2016, 18(11): 1847-1870. DOI:10.1002/adem.201600053 |
| [59] |
ALI M, ZEESHAN M, AHMED S, et al. Development and comfort characterization of 2D-woven auxetic fabric for wearable and medical textile applications[J]. Clothing and Textiles Research Journal, 2018, 36(3): 199-214. DOI:10.1177/0887302X18768048 |
 2021, Vol. 49
2021, Vol. 49