文章信息
- 赵家祥, 李建, 梁志鸿, 邱博, 阚前华
- ZHAO Jia-xiang, LI Jian, LIANG Zhi-hong, QIU Bo, KAN Qian-hua
- 超弹性NiTi合金率相关相变图案演化模拟
- Simulation on rate-dependent transformation pattern evolution of super-elastic NiTi alloy
- 材料工程, 2021, 49(4): 102-110
- Journal of Materials Engineering, 2021, 49(4): 102-110.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000672
-
文章历史
- 收稿日期: 2020-07-23
- 修订日期: 2020-12-14
超弹性NiTi合金作为一种性能优良的形状记忆合金,一经问世就引起学者们的广泛关注。除了对其在各种加载工况下的力学响应以及本构模型进行研究之外[1-2],加/卸载过程中的相变图案演化也吸引着研究者们的关注。实验研究发现,超弹性NiTi合金构件(微管、薄板)受拉时表面会出现吕德斯带(Lüders bands)[3-4],与金属位错机制所致的局部变形不同,该现象由应力诱发马氏体相变所致。马氏体相变过程中的潜热释放与吸收影响了相变应力[5-6],从而导致相变图案发生演化,其具有显著的热-力耦合特征。超弹性NiTi合金板的拉伸实验发现,随着加载应变率的提高,试样表面最大相变条带的数量增多,与其对应位置的材料表面温度也随之提高[7-8],即相变图案的演化依赖于加载应变率;同时,相变图案演化的率相关性还影响应力-应变曲线,相变带的萌生导致应力-应变曲线上出现应力跌落现象[7, 9],应变率的增加导致相变硬化增加[10-11]。超弹性NiTi合金相变图案演化与其热力学响应密切相关,开展该类现象的研究将有助于揭示超弹性NiTi合金相变图案演化机理。
随着计算机科学技术和有限元方法的飞速发展,许多学者通过数值模拟来重现超弹性NiTi合金的相变图案演化。例如,Shaw和Kyriakides[3]基于多线性本构模型,类比低碳钢拉伸时吕德斯带的萌生与扩展行为,将应力诱发马氏体相变过程视为不可逆的塑性流动,重现了超弹性NiTi合金薄板在拉伸过程中的相变图案演化过程,且该方法被胡振东等[12]进一步拓展到薄壁圆管的相变图案演化模拟中。Shaw[13]基于多线性本构模型,考虑相变过程中的热-力耦合效应,成功模拟了超弹性NiTi合金薄板在拉伸过程中的相变带图案演化和温度场演化规律。Jiang等[14-15]通过在ABAQUS中实现马氏体相变本构模型,成功模拟了超弹性NiTi合金薄板在拉伸、压缩和扭转过程中相变图案的演化。Iadicola等[9]进一步模拟了不同环境介质下超弹性NiTi合金细丝拉伸时相变带数量变化、温度场和应力场演化。已有工作为超弹性NiTi合金率相关相变图案演化模拟提供了较好的思路和技术路径,然而它们对于不同加载应变率下超弹性NiTi合金相变图案演化机理还缺乏深入分析,尤其是对相变带的形成机制、锋面扩展、温度场变化及其对加载应变率的依赖关系研究还不够充分。
本工作基于有限元软件ABAQUS/Standard,通过不同温度下的实验应力-应变曲线确定多线性本构模型参数,通过热物理参数等效方法来考虑相变潜热的释放,对超弹性NiTi合金薄板在拉伸过程中相变图案演化的率相关性进行数值模拟,详细讨论不同应变率下的相变带萌生、扩展与合并规律,并与实验观察结果进行对比,从而深入揭示超弹性NiTi合金率相关相变图案演化机理。
1 有限元模型根据Zhang等[8]采用的试件尺寸建立有限元模型,如图 1(a)所示。试件长度L=60.0 mm,工作段l=30.0 mm,宽度w=2.6 mm,厚度t=0.5 mm。采用热-位移耦合单元C3D8HT划分网格,宽度方向和长度方向单元长度为0.1 mm,厚度方向单元长度为0.0625 mm。由于夹持端处于弹性变形范围,网格划分较为稀疏。在试件表面建立局部坐标系,如图 1(a)所示,确定坐标原点位于试样下端中心。建模时厚度方向取1/2,并施加对称约束,其他位置的位移约束和初始温度如式(1)所示:
|
图 1 薄板拉伸有限元模型 (a)几何尺寸和网格;(b)初始缺陷类型 Fig. 1 Finite element model of thin plate tension (a)geometrical size and mesh; (b)initial dent type |
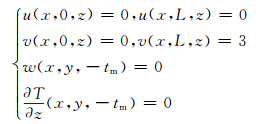
|
(1) |
式中:T为试样温度;u,v,w分别为x,y,z三个方向的位移;tm为厚度t的1/2。
通过对已有的相变带演化实验结果[8]分析可知,相变带更容易从试样过渡段处萌生,其原因是该处加工缺陷容易产生应力集中。因此,在过渡段位置施加不同尺寸的初始缺陷进行模拟。这里考虑Ⅰ型与Ⅱ型两类初始缺陷,如图 1(b)所示。两类缺陷厚度方向均贯穿试件,即tm=0.25 mm,长度均为ldⅠ=ldⅡ=2tm,宽度分别取dⅠ=0.1tm,dⅡ=0.05tm,缺陷形状为梯形。
2 材料模型为了模拟超弹性NiTi合金相变过程中相变形核应力大于相变开始应力从而引起的失稳现象,可将应力-应变关系简化为三段线性分别描述奥氏体弹性变形、应力诱发马氏体相变、马氏体弹性变形三个变形阶段[3],具体表达如式(2)所示:
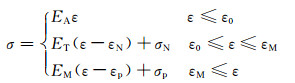
|
(2) |
式中:EA和EM分别为奥氏体与马氏体的弹性模量;ET为马氏体相变硬化模量;σN为相变开始应力;σP为相变结束应力;ε,ε0和εM分别为当前应变,相变开始处的弹性应变与单轴最大相变应变。
通过实验得到材料在22, 36, 50, 70, 90 ℃下的单调拉伸应力-应变曲线(见图 2虚线)。由于实验中相变形核后突然出现应力跌落,在有限元模拟中将产生收敛问题,这里按照图示方法确定相变开始应力σN和结束应力σP后,按照本构方程式(2)对应力-应变曲线进行修正[13](见图 2实线),获得过渡平缓的相变应力变化,从而可以考虑相变失稳过程。

|
图 2 超弹性NiTi合金不同温度下实验和模拟的拉伸应力-应变曲线 Fig. 2 Experimental and simulated tensile stress-strain curves of super-elastic NiTi alloy at different temperatures |
宏观上,由于相变带图案演化与低碳钢的吕德斯带变形过程相似,可将应力诱发马氏体相变过程视为不可逆的塑性流动[3],只研究超弹性NiTi合金薄带拉伸过程中相变图案演化以及热-力耦合变形行为。为模拟率相关的相变图案演化,需要输入的热物理常数参考He等[16]的工作,具体如表 1所示。
超弹性NiTi合金的马氏体相变为一级相变,相变潜热远大于塑性耗散生热,因此无法通过ABAQUS中的塑性耗散生热系数来考虑。Shaw[13]提出了热物理常数等效方法来考虑相变潜热效应:首先根据比塑性功率可计算出生热率:
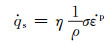
|
(3) |
式中: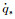
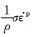
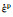
马氏体相变潜热释放可由式(4)计算:
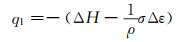
|
(4) |
式中:ql代表相变潜热释放的热能,可分解为应力相关项与应力无关项:ΔH为应力无关项,表征温度诱发马氏体相变时的焓变;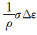
相变潜热在数值上可通过塑性耗散生热进行等效,令qs=ql,通过对式(3)进行积分并联合式(4)可得等效系数:
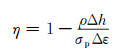
|
(5) |
由式(5)可计算出在22, 36, 50, 70, 90 ℃下,η分别为7.52, 5.72, 4.56, 3.87, 3.38。
获得不同温度下的等效系数η值后,将比热系数、热传导系数、热对流系数通过η值进行缩放,从而获得考虑相变潜热时的修正温度场。进而在ABAQUS中输入图 1所示的应力-应变曲线数据点和不同温度等效后的热物理常数,采用瞬态温度-位移耦合分析,对超弹性NiTi合金薄板进行热-力耦合拉伸过程模拟。
需要说明的是,超弹性NiTi合金的率效应与金属材料不同(金属材料的率相关性一般由黏塑性或蠕变引起),其主要原因是热-力耦合作用:由于相变潜热释放,导致材料内部温度升高;同时由于奥氏体在高温下更加稳定,导致奥氏体向马氏体转变所需的驱动应力升高,出现相变硬化效应;加载速率越高,温升越高,马氏体相变驱动力越大,相变硬化效应就越明显,即应力-应变曲线体现出率效应。因此,采用ABAQUS中考虑温度相关的弹塑性模型,通过物理参数等效来考虑相变潜热,施加热边界条件来考虑内部温升与外界热交换的竞争作用,进而模拟应力-应变曲线的率效应。
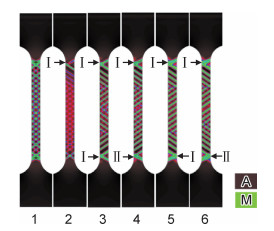
3 结果与讨论图 3显示了缺陷Ⅰ, Ⅱ预制方式对相变带图案的影响。由图 3可知,未预制缺陷试样的相变带从两侧同时萌生,呈交叉状;第2种为单侧预制缺陷,试件一端也出现了交叉的相变带;第3~6种情况下模拟的相变带清晰可见,其形状与个数也十分接近,即当缺陷预制位置相同时,缺陷类型Ⅰ和Ⅱ对相变带图案演化影响不大,后续分析中将采用第4种缺陷预制形式进行讨论。
|
图 3 初始缺陷对相变带演化的影响 Fig. 3 Effects of initial defects on the evolutions of transformation pattern |
图 4给出了应变率为3.33×10-3s-1时,拉伸过程中实验与模拟的相变带图案和温度场分布。由图 4(a)可知,相变带从试样缺陷处萌生,随着拉伸应变的增加,相变带逐渐扩展,并逐渐萌生更多的相变带;相变过程中出现了两种方向的相变带,它们与加载方向夹角分别为51°和60°,这与模拟结果图 4(b)十分接近。测量数值模拟中相变带与加载方向夹角,发现其也在Lomer[17]观测的48°~65°和Butler[18]观测的50°~70°夹角范围内。结合图 4(c)可知,相变潜热导致局部温升,根据Clausius-Clapeyron关系[19],相变扩展应力σP随着温升的增加而增大[19],进一步使薄板整体平均的应力响应增加;应力一旦达到薄板低温区的相变应力σN时,将诱发较低温处材料先发生马氏体相变,如此循环往复,导致相变带从不同位置不断萌生与扩展;当相变带增至一定数量后开始合并,直至薄板工作段全部完成相变。观察拉伸过程中的温度场演化可以发现,马氏体相变导致材料局部温度升高,形成不均匀温度场,随着不同相变带锋面的移动与合并,材料表面温度逐渐升高,直到相变带合并全部完成,材料表面温度达到最大值。对比数值模拟与实验的温度场分布发现,模拟结果与实验结果具有相似的演化规律,数值上也较为接近,如图 4(c)和图 4(d)所示。
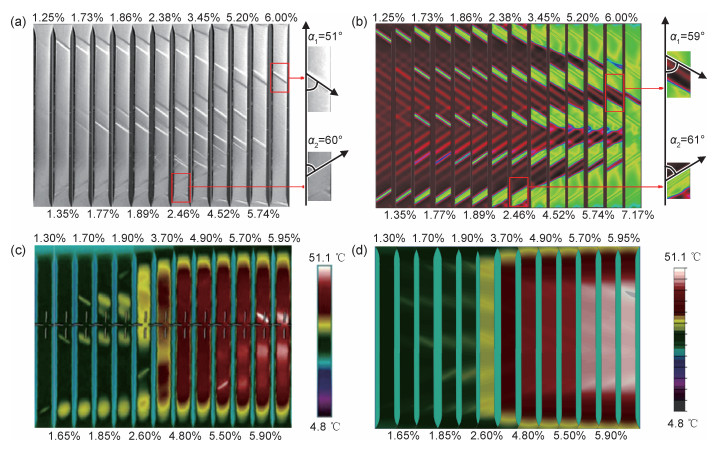
|
图 4 应变率为3.33×10-3 s-1时试样表面相变带图案和温度场演化 (a)实验相变带[8];(b)模拟相变带;(c)实验温度场[8];(d)模拟温度场 Fig. 4 Evolutions of transformation bands and temperature field with strain rate of 3.33×10-3 s-1 (a)experimental transformation bands[8]; (b)simulated transformation bands; (c)experimental temperature field[8]; (d)simulated temperature field |
图 5(a)显示了拉伸过程中模拟和实验的名义应力-应变曲线,即试样工作段平均的应力-应变曲线。可以观察到,当相变带萌生以及锋面合并时,名义应力-应变曲线将会出现应力下降现象。由于相变潜热释放导致相变应力不断增加,名义应力-应变曲线出现应变硬化现象。进一步提取拉伸过程中相变带数量随名义应变的变化曲线,如图 5(b)所示。可以看出,实验和模拟的最大相变带数量一致,相变带数量均是先增加再减少,即相变带萌生、扩展和合并过程。
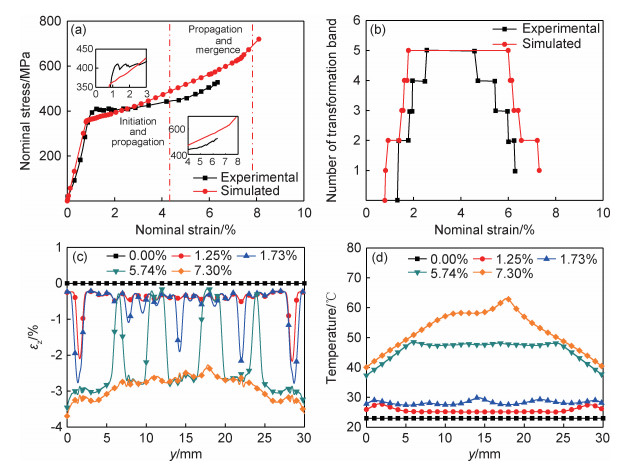
|
图 5 应变率为3.33×10-3 s-1时定量分析结果 (a)实验与数值模拟的名义应力-应变曲线[8];(b)实验和模拟的相变带数量[8];(c)εz沿加载方向的演化;(d)试件表面温度沿加载方向的演化 Fig. 5 Quantitative analysis results with strain rate of 3.33×10-3 s-1 (a)experimental and simulated nominal stress-strain curves[8]; (b)the number of experimental and simulated transformation bands[8]; (c)evolution of εz along loading direction; (d)evolution of specimen surface temperature along loading direction |
通过数值模拟可以很方便地对应变场和温度场分布进行定量分析。图 5(c), (d)绘制了拉伸过程中试样工作段位于Y轴(见图 1)上节点应变εz和温度的分布曲线。由图 5(c)可观察到,随着相变带的不断萌生与扩展,产生的应变峰不断增加;随着相变带的合并,相变逐渐全部完成,节点应变εz趋于均匀。观察不同加载名义应变时εz和温度的分布(见图 5(c)),明显可见温升方向随着相变带萌生、扩展与合并而变化;由于相变完成后材料局部不再产生新的相变潜热释放,再考虑到试样两端表面先与环境进行热交换,导致相变结束后试件中部温度高于两端约20 ℃。
图 6给出了应变率为3.33×10-2 s-1时,拉伸过程中实验与模拟的相变带图案和温度场演化过程。对比应变率为3.33×10-3 s-1时的实验结果发现,较高速率下的相变带萌生数量增加,试件表面温度更高。这是材料相变潜热释放以及材料表面与环境进行热交换的竞争结果:较高应变率下由于热量不能及时散出,导致材料相变局部温升增加,进而导致相变扩展应力增大,更容易在未相变的低温区域萌生更多的相变带。

|
图 6 应变率为3.33×10-2 s-1时试样表面相变带图案和温度场演化 (a)实验相变带[8];(b)模拟相变带;(c)实验温度场[8];(d)模拟温度场 Fig. 6 Evolutions of transformation pattern and temperature field with strain rate of 3.33×10-2 s-1 (a)experimental transformation bands[8]; (b)simulated transformation bands; (c)experimental temperature field[8]; (d)simulated temperature field |
图 7(a)显示了加载过程中实验与模拟的名义应力-应变曲线,相比于较低应变率下(3.33×10-3 s-1,蓝色实线),较高应变率导致相变硬化增强,数值模拟结果与实验结果吻合较好;另外,较高应变率下名义应力-应变曲线变得相对光滑,相变带萌生与扩展时的应力下降现象不再明显,这是由于较高应变率下局部温升更加明显,相变硬化增强所致。已有的实验研究也发现[8, 11],随着加载应变率的增加,名义应力-应变曲线将由等温状态转变为绝热状态,同时从应力跌落曲线向光滑曲线转变。图 7(b)显示了拉伸过程中相变带数量随着名义应变的变化,可以看出,在相变带萌生与扩展阶段,相变带数量随名义应变的增加而增加;在相变带合并阶段,相变带数量随名义应变的增加而减少,模拟结果与实验结果趋势上吻合较好,但模拟的相变带数量的峰值高于实验结果。图 7(c), (d)分别给出了拉伸过程中试样工作段Y轴上节点应变εz和温度的变化曲线。对比图 6(c)和图 7(c)可以看出,较高应变率下的相变带萌生数量增多,与之对应的温度分布也更加均匀,温升更高,这是由于高应变率下热量与外界交换较少所致。

|
图 7 应变率为3.33×10-2 s-1时定量分析结果 (a)实验与数值模拟的名义应力-应变曲线[8];(b)实验与数值模拟的相变带数量[8];(c)εz沿加载方向的演化;(d)试件表面温度沿加载方向的演化 Fig. 7 Quantitative analysis results with strain rate of 3.33×10-2 s-1 (a)experimental and simulated nominal stress-strain curves[8]; (b)number of experimental and simulated transformation bands[8]; (c)evolutions of εz along the loading direction; (d)evolution of specimen surface temperature along loading direction |
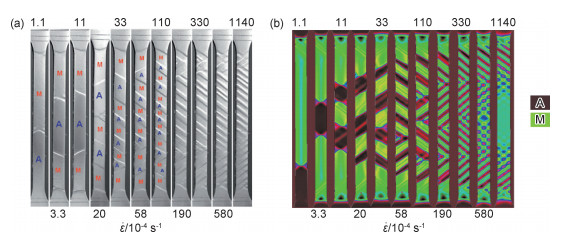
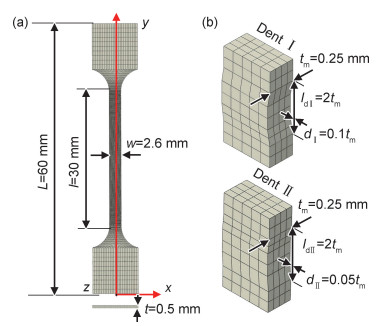
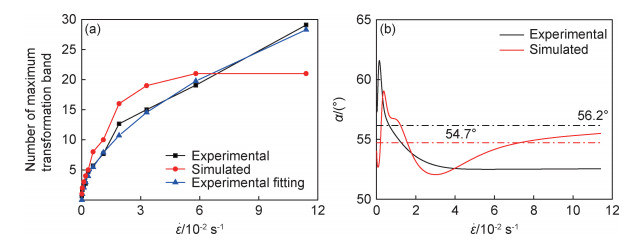
实验和模拟的不同应变率下的相变带图案对比如图 8所示。可以清晰看到,由于相变潜热的释放以及试样表面与环境热交换的共同作用,相变带的数量随着应变率的增大而增加,实验结果和模拟结果呈现出相同的趋势。
He等[16]推导得出最大相变带数量与加载应变率之间满足关系式(6):
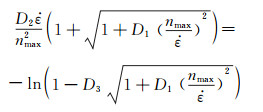
|
(6) |
其中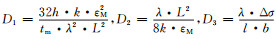
| Latent heat/(mJ·mm-3) | Heat capacity/(J·m-3·℃-1) | Transformation strain/% | Isothermal stress drop/MPa | Temperature coefficient of transformation stress/(MPa·℃-1) |
Specimen length/mm | Half strip’s thickness/mm |
| 96.8 | 3.2×106 | 4.8 | 18 | 5.7 | 30 | 0.25 |
|
图 9 不同应变率下最大相变带数量随应变率的变化曲线(a)以及相变锋面与拉伸方向的平均夹角(b) Fig. 9 Curves of the number of maximum transformation bands with the strain rate (a) and average angles between transformation front and axial direction (b) at different strain rates |
不同加载应变率下马氏体相变完成后Y轴上节点应变εz和温度沿加载方向的演化曲线如图 10所示。由图 10(a)可知,高应变率下(1.9×10-2~1.1×10-1 s-1),相变完成后应变分布较为均匀,而其他加载工况下由于相变带于两端萌生,且相变带数量较少,试件两端相变锋面上εz要高于试件中部。图 10(b), (c)给出了不同应变率下模拟所得的温度场演化曲线以及名义应力-应变曲线。可以观察到,随着加载速率的提高,相变潜热不能及时与外界进行热交换,导致温度升高,马氏体相变过程逐渐由等温状态向绝热状态转变。根据Clausius-Clapeyron关系,材料发生相变所需的驱动应力也随之增大,导致相变硬化增强,该位置马氏体相变更加困难,从而促进材料在较低温度区域发生相变,增加了局部相变带个数,进而影响相变图案演化。

|
图 10 不同应变率下的模拟结果 (a)εz沿加载方向的演化;(b)温度沿加载方向的演化;(c)名义应力-应变曲线 Fig. 10 Simulated results at different strain rates (a)evolution of εz along the loading direction; (b)evolution of temperature along the loading direction; (c)nominal stress-strain curves |
综上所述,超弹性NiTi合金相变图案演化的率相关性可归结于热-力耦合作用和材料温度敏感性的共同作用:在加载应变率较低时,由于相变潜热有充足的时间与环境进行热交换,因而温升很小,试样温度在拉伸过程中近似均匀分布;由于应力集中,相变带仅从初始缺陷处萌生,并不断向未相变区域进行扩展;当加载应变率较高时,相变带从缺陷处萌生,该处由于相变潜热的快速释放(相变潜热释放时间与热交换时间存在时间差),材料内部储存热量来不及与外界进行充分热交换,导致相变处的温度迅速升高;由于材料的温度敏感性,温度越高,马氏体相变所需的应力越大,一旦温度升高引起的相变应力超过其他未相变区域的相变开始应力,相变将优先从其他区域萌生;下一个萌生位置将会重复此过程,最终导致加载速率越高,相变萌生位置的迁移越快,可迁移的区域越充分,相变带数量就越多,从而体现出显著的率相关相变图案演化。
4 结论(1) 试样拉伸时表面萌生局部相变带,与加载方向成一定夹角,并随机出现两种取向,该夹角在50°~65°之间,模拟结果与实验结果接近。
(2) 相变带在初始缺陷处产生,其数量先增加再减少,即相变带经历萌生、扩展和合并的过程;相变完成后试件厚度方向的应变在高应变率下分布更为均匀。
(3) 萌生的局部相变带诱导局部温升,形成非均匀温度场分布,分布规律与应变场类似;由于相变扩展应力随温升的增加而增大,提高了材料的平均应力,相变扩展受阻,在温度低的区域更容易发生马氏体相变,从而导致更多的相变带萌生,直至相变全部完成。
(4) 由于相变潜热与热交换存在时间差,随着加载应变率的增加,试样从等温状态逐步过渡到绝热状态,最大相变带数量随着加载应变率的增加而增多,模拟结果与实验结果和已有解析结果在较低应变率下较为吻合,在较高应变率时低于实验结果。
| [1] |
周廷, 阚前华, 康国政, 等. 超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型[J]. 力学学报, 2017, 49(3): 588-596. ZHOU T, KAN Q H, KANG G Z, et al. A macroscopic phenomenological constitutive model for the uniaxial transformation ratcheting of super-elastic NiTi shape memory alloy[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 588-596. |
| [2] |
YU C, KANG G Z, KAN Q H. A micromechanical constitutive model for grain size dependent thermo-mechanically coupled inelastic deformation of super-elastic NiTi shape memory alloy[J]. International Journal of Plasticity, 2018, 105: 99-127. DOI:10.1016/j.ijplas.2018.02.005 |
| [3] |
SHAW J A, KYRIAKIDES S. Initiation and propagation of localized deformation in elasto-plastic strips under uniaxial tension[J]. International Journal of Plasticity, 1997, 13(10): 837-871. DOI:10.1016/S0749-6419(97)00062-4 |
| [4] |
HAJIDEHI M R, STUPKIEWICZ S. Gradient-enhanced model and its micromorphic regularization for simulation of Lüders-like bands in shape memory alloys[J]. International Journal of Solids and Structures, 2018, 135: 208-218. DOI:10.1016/j.ijsolstr.2017.11.021 |
| [5] |
XIAO Y, ZENG P, LEI L P, et al. In situ observation on temperature dependence of martensitic transformation and plastic deformation in superelastic NiTi shape memory alloy[J]. Materials & Design, 2017, 134: 111-120. |
| [6] |
YU C, KANG G Z, KAN Q H. A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy: one-dimensional model[J]. Mechanics of Materials, 2014, 78: 1-10. DOI:10.1016/j.mechmat.2014.07.011 |
| [7] |
SHAW J A, KYRIAKIDES S. On the nucleation and propagation of phase transformation fronts in a NiTi alloy[J]. Acta Materialia, 1997, 45(2): 683-700. DOI:10.1016/S1359-6454(96)00189-9 |
| [8] |
ZHANG X H, FENG P, HE Y J, et al. Experimental study on rate dependence of macroscopic domain and stress hysteresis in NiTi shape memory alloy strips[J]. International Journal of Mechanical Sciences, 2010, 52(12): 1660-1670. DOI:10.1016/j.ijmecsci.2010.08.007 |
| [9] |
IADICOLA M A, SHAW J A. Rate and thermal sensitivities of unstable transformation behavior in a shape memory alloy[J]. International Journal of Plasticity, 2004, 20(4/5): 577-605. |
| [10] |
YANG Z L, WANG H, HUANG Y L, et al. Strain rate dependent mechanical response for monoclinic NiTi shape memory alloy: micromechanical decomposition and model validation via neutron diffraction[J]. Materials & Design, 2020, 191: 108656. |
| [11] |
KAN Q H, YU C, KANG G Z, et al. Experimental observations on rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy[J]. Mechanics of Materials, 2016, 97: 48-58. DOI:10.1016/j.mechmat.2016.02.011 |
| [12] |
胡振东, 孙庆平. 超弹性形状记忆合金管单向拉伸试验的数值模拟[J]. 力学季刊, 2005, 26(3): 389-392. HU Z D, SUN Q P. Numerical simulation for tension experiment of superelastic shape memory alloys tube[J]. Chinese Quarterly of Mechanics, 2005, 26(3): 389-392. DOI:10.3969/j.issn.0254-0053.2005.03.010 |
| [13] |
SHAW J A. Simulations of localized thermo-mechanical behavior in a NiTi shape memory alloy[J]. International Journal of Plasticity, 2000, 16(5): 541-562. DOI:10.1016/S0749-6419(99)00075-3 |
| [14] |
JIANG D J, BECHLE N J, LANDIS C M, et al. Buckling and recovery of NiTi tubes under axial compression[J]. International Journal of Solids and Structures, 2016, 80: 52-63. DOI:10.1016/j.ijsolstr.2015.10.022 |
| [15] |
JIANG D J, KYRIAKIDES S, LANDIS C M, et al. Modeling of propagation of phase transformation fronts in NiTi under uniaxial tension[J]. European Journal of Mechanics-A/Solids, 2017, 64: 131-142. DOI:10.1016/j.euromechsol.2017.02.004 |
| [16] |
HE Y J, SUN Q P. Rate-dependent domain spacing in a stretched NiTi strip[J]. International Journal of Solids and Structures, 2010, 47(20): 2775-2783. DOI:10.1016/j.ijsolstr.2010.06.006 |
| [17] |
LOMER W M. The yield phenomenon in polycrystalline mild steel[J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 64-73. DOI:10.1016/0022-5096(52)90007-0 |
| [18] |
BUTLER J F. Lüders front propagation in low carbon steels[J]. Journal of the Mechanics and Physics of Solids, 1962, 10(4): 313-318. DOI:10.1016/0022-5096(62)90003-0 |
| [19] |
GRASSI E N D, CHAGNON G, De OLIVEIRA H M R, et al. Anisotropy and Clausius-Clapeyron relation for forward and reverse stress-induced martensitic transformations in polycrystalline NiTi thin walled tubes[J]. Mechanics of Materials, 2020, 146: 103392. DOI:10.1016/j.mechmat.2020.103392 |
 2021, Vol. 49
2021, Vol. 49