文章信息
- 刘敬勇, 卢磊, 钟政烨
- LIU Jing-yong, LU Lei, ZHONG Zheng-ye
- 高应变速率下等径角挤压高纯粗晶铝中的形变孪晶与退火孪晶
- Deformation twins and annealing twins in high purity coarse-grained aluminum by equal channel angular pressing at high strain rate
- 材料工程, 2021, 49(4): 89-94
- Journal of Materials Engineering, 2021, 49(4): 89-94.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000288
-
文章历史
- 收稿日期: 2020-04-02
- 修订日期: 2020-09-14
孪晶界(twin boundary,TB)作为一种特殊的大角度晶界(high angle grain boundary,HAGB),对材料的强度、塑性、韧性以及导电性等有显著的影响[1-2]。根据孪晶的形成方式,可将其分为形变孪晶、退火孪晶以及生长孪晶,这三种孪晶形成的难易均和材料的层错能相关。在Cu和Fe这类中低层错能金属中,通过大塑性变形、电解沉积以及退火等工艺可形成孪晶[3]。然而,在高层错能金属中,由于拖拽不全位错和先导不全位错的复合,使得层错恢复到正常的原子堆垛顺序[4],孪晶的形成较难。
铝的层错能约为172 mJ·m-2[5],是一种典型的高层错能金属。Han等[6]通过等径通道挤压在单晶铝中观察到少量原子级别厚度的形变孪晶和层错。对于铝合金而言,其他元素的加入有效地降低了层错能,在低应变率下就能够形成少量的形变孪晶[7]。但是高纯铝仅在某些极限条件下,如裂纹尖端、低温以及高应变率[8]下才能形成纳米尺寸的形变孪晶。Zhao等[9]通过动态等径角挤压(dynamic equal channel angular pressing, D-ECAP),即同时实现高应变率和大剪切变形(应变率约为106 s-1,剪应变约为2),在单晶铝中制备出了尺寸达到百微米级别的形变孪晶。Han等[10]认为,当晶粒尺寸大于一定值时,形成孪晶的临界剪切应力主要取决于层错能以及取向,但粗晶铝中百微米级别形变孪晶的形成仍然较困难。
传统的ECAP变形工艺应变率较低,挤压过程中温度变化不明显,如Yamaguchi等[11]发现当挤压速率从0.18 mm·s-1提高至18 mm·s-1时,高纯铝试样内部的温度由11 ℃上升至40 ℃。Kapoor等[12]发现在高应变率(3×103 s-1)绝热变形下,6061铝合金中的变形功完全转化为热时,内部温度上升幅度达到70 ℃。而D-ECAP挤压的速率能够达到数百米每秒,应变率可达到106s-1[9],温度上升幅度理论上更大,使得材料塑性变形能力提高且能够开启不同类型的滑移系[13]。此外,温度还会促使材料在塑性变形过程中发生动态再结晶。纯铜在大塑性变形过程中,内部的温升会导致动态再结晶,从而产生退火孪晶[14]。粗晶铝在D-ECAP挤压过程中能否形成退火孪晶,以及高应变率大剪切变形如何影响退火孪晶的形成,至今鲜有报道。
本研究采用D-ECAP高应变率和大剪切变形的优点,在高纯粗晶铝中同时制备出了形变孪晶以及退火孪晶,利用EBSD表征手段对比了两种孪晶之间的差异,分析了D-ECAP过程中形变孪晶和退火孪晶产生的可能方式。
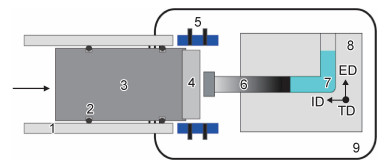
1 实验材料与方法实验材料为高纯铝(99.999%,质量分数)铸锭,晶粒尺寸在1 mm左右,将铸锭按照D-ECAP模具尺寸切割成10 mm×10 mm×30 mm的块状试样。为了减小样品在挤压过程中与内壁的摩擦力,在试样表面涂抹一层MoS2后放入外角ψ为37°、内角Φ为90°的D-ECAP模具中挤压一道次,其等效应变约为1。图 1为D-ECAP实验装置示意图,在炮筒中,压缩氦气瞬间从左侧释放推动铝弹托向右运动。为降低铝弹托与压杆撞击过程中的能量损失,在其前端粘一个厚度为4 mm的不锈钢飞片。当铝弹托携带不锈钢飞片向右飞行至激光遮断测速系统时,系统测得弹托的飞行速率约为235 m·s-1,应变率约在105~106 s-1之间。当飞片撞击到预先放置在D-ECAP模具中的压杆时,动能传递给压杆,从而推动高纯铝试样完成瞬时的等径角挤压。如图 1所示,试样插入方向用ID表示,挤出方向用ED表示,垂直于纸面向外用TD表示。限于D-ECAP实验装置的结构,无法测试挤压过程中试样具体的温度变化。
|
图 1 D-ECAP实验装置示意图 Fig. 1 Schematic diagram of D-ECAP experimental device 1-gun barrel; 2-O-ring; 3-aluminum sabot; 4-flyer plate; 5-optical beam block system; 6-driving rod; 7-sample; 8-D-ECAP die; 9-target chamber |
为减轻挤压过程中摩擦力、不同位置变形速率以及受力状态的影响,本实验仅取D-ECAP挤压后高纯铝试样中心厚度处ID-ED面心部6 mm×10 mm的矩形区域进行EBSD表征。依次将挤压后试样经400#, 800#, 1200#, 1600#和2000#砂纸打磨,SiO2悬浊液机械抛光和电解抛光(电解抛光消除制样过程中引入的残余应力和微小划痕)。电解抛光液由90 mL无水乙醇,5 mL高氯酸和5 mL去离子水组成。将经过电解抛光后的试样放入无水乙醇中进行超声清洗后,再放入配置了牛津EBSD探头的FEI Quanta 250扫描电子显微镜中进行EBSD表征,表征结果用HKL Channel 5软件分析,原始标定率在90%以上。将取向差大于15°的晶界定义为大角度晶界,形变孪晶界的标定采用Brandon准则[15],即偏离60°〈111〉 8.6°以内的为∑3孪晶界。
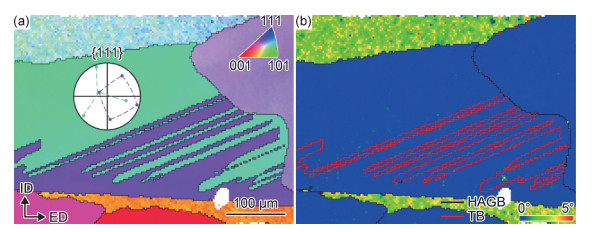
2 实验结果 2.1 形变孪晶图 2给出了经过D-ECAP挤压一道次后高纯铝中形变孪晶的EBSD表征结果,可以看出原始铸锭晶粒的晶界得到了保留,从下端晶界处产生了一簇取向相近的透镜状晶粒。图 2(a)中的插图为矩形方框内所对应的{111}极图,可以看出绿色与紫色晶粒满足孪晶关系。孪晶的片层厚度、长轴尺寸分别在15~230 μm和50~850 μm之间变化。这是因为D-ECAP变形不均匀,不同位置受到的剪切力不同而造成的,类似Lou等[16]发现镁合金中形变孪晶的片层厚度随着应变量的增加而减小。图 2(b)为该区域Kernel平均取向差(Kernel average misorientation, KAM)分布图。KAM通过计算晶粒内部相邻的扫描点之间的平均取向差,从而定性反映塑性变形的程度,KAM值越大的地方其塑性变形程度越高,而对于缺陷密度较低的再结晶晶粒而言,其KAM值往往较低[17]。图 2(b)表明整个区域经历了较大的塑性变形,但孪晶的KAM值大于周围基体,即孪晶相对于基体发生了更大的塑性变形。值得注意的是,基体接近孪晶尖端处的KAM值大于周围,这可能是孪晶界作为位错源在变形过程中不断产生位错射向基体,使得靠近孪晶尖端处的应变更大[9]。图 2(a)中划线处的取向差变化如图 2(c)所示,可以看出孪晶界两端的取向差接近于60°,部分孪晶界会偏离60°约5°左右,表明孪晶形成后经历了较大的塑性变形,使得孪晶偏离了标准的孪晶取向[9]。

|
图 2 D-ECAP变形后高纯铝中形变孪晶EBSD表征结果 (a)取向成像图;(b)图(a)对应的KAM图;(c)孪晶界取向差图 Fig. 2 EBSD results of deformation twins in high purity aluminum processed by D-ECAP (a)inverse pole figure map; (b)corresponding KAM map of fig.(a); (c)twin boundaries misorientation profile |
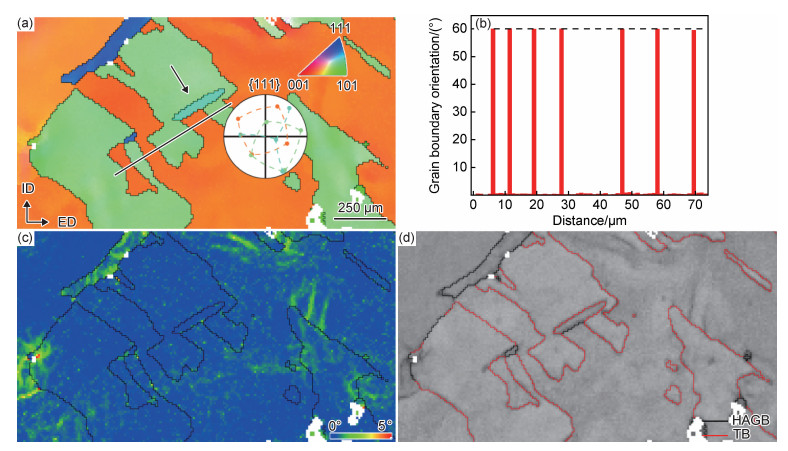
粗晶铝经过D-ECAP挤压一道次后,退火孪晶微观结构的EBSD结果如图 3所示。由图 3(a)中的插图{111}极图可知,紫色与浅绿色部分互为孪晶关系,退火孪晶界较为平直,这与图 2(a)中透镜状的孪晶不同。由图 3(b)可知,整个区域由KAM值较高的变形部分和KAM值较低的再结晶部分构成,变形部分KAM值较分散表明D-ECAP变形不均匀,再结晶部分KAM值很低,这与相关文献利用KAM值判断再结晶晶粒的结论是一致的[18]。由此可知,图 3中孪晶界两端的晶粒均为再结晶晶粒,与图 2(c)中形变孪晶存在较大区别。此外,图 3(b)中的孪晶界(红线)是以偏离∑3 60°〈111〉 2°以内标定,这也符合退火孪晶的特点。类似的情况在D-ECAP变形后高纯铝中退火孪晶EBSD表征结果(图 4)中也存在。图 4(a)中的插图为中部区域对应的{111}极图,该区域存在两种孪晶关系的退火孪晶,即黄色与浅绿色部分互为孪晶关系,浅绿色与箭头所指的青色晶粒互为孪晶关系。结合图 4(d)可知,退火孪晶界形态较为不规则(红线表示孪晶界),这是由于不均匀变形导致局部储存能存在差异,退火孪晶在后续的长大过程中朝着储存能高的地方生长[19]。图 4(a)划线处的孪晶界取向差如图 4(b)所示,退火孪晶界的取向差等于60°。图 4(c)表明整个区域基本上发生了再结晶,其KAM值接近于0°。
|
图 3 D-ECAP变形后高纯铝中退火孪晶微观结构的EBSD表征结果 (a)取向成像图;(b)图(a)对应的KAM图 Fig. 3 EBSD results of microstructure of annealing twins in high purity aluminum processed by D-ECAP (a)inverse pole figure map; (b)corresponding KAM map of fig.(a) |
|
图 4 D-ECAP变形后高纯铝中退火孪晶EBSD表征结果 (a)取向成像图;(b)孪晶界取向差图;(c)图(a)对应的KAM图;(d)菊池带衬度分布图 Fig. 4 EBSD results of annealing twins in high purity aluminum processed by D-ECAP (a)inverse pole figure map; (b)twin boundaries misorientation profile; (c)corresponding KAM map of fig.(a); (d)Kikuchi band contrast map |
多晶铝中当晶粒尺寸小于15 nm时,位错形成的临界应力高于形变孪晶,因此形变孪晶容易形成[20]。当晶粒尺寸逐渐增大时,形变孪晶形成的临界剪切应力大于位错滑移,变形以位错滑移的方式进行,此时多晶铝中的形变孪晶较难形成[10]。但D-ECAP是一种结合高应变率和大剪切变形的加载方式,其局部剪切应力能够达到1.5 GPa,大于粗晶铝中孪晶形成所需的临界剪切应力(≈1 GPa)[9-10],并且高应变率变形条件下,位错的缠结会抑制位错进一步的运动[21],且大的剪切变形在极短的时间内完成。在这种情况下,高应变率下的大剪切变形需要额外的变形机制去协调变形,导致高层错能金属铝中出现形变孪晶。因此,当粗晶铝经过D-ECAP转角处时,某些取向的晶粒受到的剪切应力大于孪晶形成所需的临界剪切应力。大剪切力将推动相邻的{111}面不断释放Shockley不全位错从而形成形变孪晶[22]。
研究发现铝在静态再结晶过程中仅形成很少的∑3 60°〈111〉晶界[23],而本研究发现,粗晶铝在D-ECAP挤压过程中就产生了较多的退火孪晶。Cahoon等[24]发现每单位长度的退火孪晶密度(ρ)与残余应变(s)、层错能(γ)、晶界能(δ)以及晶粒尺寸(d)相关,并遵循以下关系:
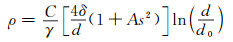
|
(1) |
式中:C和A是常数;d0是孪晶形核的临界晶粒尺寸,低于此尺寸,退火孪晶将无法形成,且Al的层错能较高,根据式(1)可知退火孪晶很难形成。但在D-ECAP高应变率、大剪切变形过程中铝中的退火孪晶相对容易形成。高应变率变形产生的位错分布更均匀且形成的位错胞较小,位错被困在位错胞内,阻碍了位错重排及动态回复过程,因此变形基体中的位错密度较高[21],引起铝在D-ECAP变形过程中的储存能更高,即残余应变s更大;而且储存能越高,孪晶形核的临界晶粒尺寸d0越小[25]。结合式(1)可知,高应变率促进了铝中退火孪晶的形成。关于大剪切变形的作用,Field等[26]发现,相同应变量下,经过剪切变形的纯铜退火后能产生更多的退火孪晶,这是因为残余剪切变形能促进Shockley不全位错的产生,从而促进退火孪晶的形成。
退火孪晶形成机制表明,退火孪晶的密度随着晶界迁移速率的增加而增加[27]。在D-ECAP挤压过程中,晶界迁移速率加快主要有以下原因:第一,粗晶铝经过高应变率剪切变形产生了更高的储存能,使得再结晶晶粒与变形基体之间的能量梯度增加;第二,由于孪晶形成的临界晶粒尺寸d0减小,使得晶界的曲率增加;第三,动态挤压过程中,温度上升幅度较大。上述原因使得晶界迁移速率提高[25, 28],从而增加{111}界面上出现层错的概率,促进退火孪晶的形成。此外,本实验形变孪晶的形成可能是因为D-ECAP变形过程中形成大量层错[9],层错有助于退火孪晶的形成。
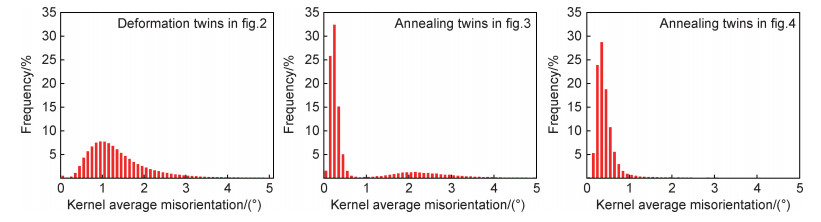
粗晶铝中透镜状形变孪晶形成后,孪晶界与位错相互作用将会导致孪晶面取向的改变[29]。协调变形使得孪晶与基体之间相互旋转,致使孪晶与基体的取向差可能偏离∑3 60°〈111〉±8.6°。此外,由于形变孪晶的施密特因子大于基体,后续塑性变形程度更高。图 5统计了图 2~4中的KAM值,形变孪晶与退火孪晶的KAM值分布存在较大区别,整体上形变孪晶的不均匀塑性变形程度较高且KAM值主要集中于0.6°~1.8°,退火孪晶的KAM值分布主要集中于0.2°~0.5°。图 3中由再结晶晶粒与变形基体两部分构成,其KAM柱状图出现了两个峰,归因于D-ECAP挤压时间短,动态再结晶不充分。粗晶铝中退火孪晶的形成消耗了形变储存能,因此KAM值较低且孪晶界两侧的取向差更接近于60°,但退火孪晶的长大过程受到储存能和曲率等因素的影响,孪晶沿着不同方向的长大速率不同[19],故存在不规则形态的退火孪晶界(见图 4)。但D-ECAP实际上包含了剪切、拉伸和压缩三种变形方式,本研究在表征区域的不同位置都发现了形变/退火孪晶的存在,故起始材料结构的不均匀性也许对孪晶在高应变率大剪切变形下的形成影响更大。此外,不同位置的应变率和受力状态也存在较大差异。因此,材料内部的变形以及再结晶行为更加复杂,需要更多的实验数据来阐明其机理。
4 结论(1) 利用D-ECAP加载手段在高纯粗晶铝中同时制备出形变孪晶和退火孪晶。
(2) D-ECAP高应变率和大剪切变形使高层错能铝中形成了百微米级的形变孪晶,其形态为透镜状,孪晶形成后由于发生了二次变形,使得孪晶界偏离∑3 60°〈111〉且整体KAM值集中于0.6°~1.8°。
(3) 高应变率剪切变形下形成的大量层错和复杂的位错组态以及高储存能在变形温升作用下促进了退火孪晶的形成。孪晶形态较为不规则,孪晶界两侧更接近∑3 60°〈111〉且其KAM值主要集中于0.2°~0.5°。
| [1] |
宋广胜, 纪开盛, 张士宏. AZ31镁合金棒材循环扭转变形及其对力学性能的影响[J]. 材料工程, 2019, 47(9): 46-54. SONG G S, JI K S, ZHANG S H. Cyclic torsion of AZ31 magnesium alloy rod and its effect on mechanical property[J]. Journal of Materials Engineering, 2019, 47(9): 46-54. |
| [2] |
LU L, SHEN Y, CHEN X, et al. Ultrahigh strength and high electrical conductivity in copper[J]. Science, 2004, 304(5669): 422-426. DOI:10.1126/science.1092905 |
| [3] |
卢磊, 卢柯. 纳米孪晶金属材料[J]. 金属学报, 2010, 46(11): 1422-1427. LU L, LU K. Metallic materials with nano-scale twins[J]. Acta Metallurgica Sinica, 2010, 46(11): 1422-1427. |
| [4] |
HUNTER A, BEYERLEIN I J. Stacking fault emission from grain boundaries: material dependencies and grain size effects[J]. Materials Science and Engineering: A, 2014, 600: 200-210. DOI:10.1016/j.msea.2014.02.030 |
| [5] |
董明慧, 韩培德, 张彩丽, 等. Al-Mg合金中层错和孪晶形变能的第一性原理研究[J]. 金属学报, 2011, 47(5): 573-577. DONG M H, HAN P D, ZHANG C L, et al. First-principles study of stacking fault energy and deformation twin energy in Al-Mg alloys[J]. Acta Metallurgica Sinica, 2011, 47(5): 573-577. |
| [6] |
HAN W, CHENG G, LI S, et al. Deformation induced microtwins and stacking faults in aluminum single crystal[J]. Physical Review Letters, 2008, 101(11): 115505. DOI:10.1103/PhysRevLett.101.115505 |
| [7] |
刘满平, 王俊, 蒋婷慧, 等. 高压扭转大塑性变形Al-Mg铝合金中的层错和形变孪晶[J]. 中国有色金属学报, 2014, 24(6): 1383-1392. LIU M P, WANG J, JIANG T H, et al. Stacking faults and deformation twins in Al-Mg alloys subjected to high pressure torsion[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1383-1392. |
| [8] |
CAO B, DAPHALAPURKAR N P, RAMESH K T. Ultra-high-strain-rate shearing and deformation twinning in nanocrystalline aluminum[J]. Meccanica, 2015, 50(2): 561-574. DOI:10.1007/s11012-014-9952-7 |
| [9] |
ZHAO F, WANG L, FAN D, et al. Macrodeformation twins in single-crystal aluminum[J]. Physical Review Letters, 2016, 116(7): 075501. DOI:10.1103/PhysRevLett.116.075501 |
| [10] |
HAN W, ZHANG Z, WU S, et al. Combined effects of crystallographic orientation, stacking fault energy and grain size on deformation twinning in fcc crystals[J]. Philosophical Magazine, 2008, 88(24): 3011-3029. DOI:10.1080/14786430802438168 |
| [11] |
YAMAGUCHI D, HORITA Z, NEMOTO M, et al. Significance of adiabatic heating in equal-channel angular pressing[J]. Scripta Materialia, 1999, 41(8): 791-796. DOI:10.1016/S1359-6462(99)00233-X |
| [12] |
KAPOOR R, NEMATN S. Determination of temperature rise during high strain rate deformation[J]. Mechanics of Materials, 1998, 27(1): 1-12. DOI:10.1016/S0167-6636(97)00036-7 |
| [13] |
PEROCHEAU F, DRIVER J. Slip system rheology of Al-1% Mn crystals deformed by hot plane strain compression[J]. International Journal of Plasticity, 2002, 18(2): 185-202. DOI:10.1016/S0749-6419(00)00075-9 |
| [14] |
LUGO N, LLORCA N, CABRERA J, et al. Microstructures and mechanical properties of pure copper deformed severely by equal-channel angular pressing and high pressure torsion[J]. Materials Science and Engineering: A, 2008, 477(1/2): 366-371. |
| [15] |
BRANDON D. The structure of high-angle grain boundaries[J]. Acta Metallurgica, 1966, 14(11): 1479-1484. DOI:10.1016/0001-6160(66)90168-4 |
| [16] |
LOU C, ZHANG X, DUAN G, et al. Characteristics of twin lamellar structure in magnesium alloy during room temperature dynamic plastic deformation[J]. Journal of Materials Science & Technology, 2014, 30(1): 41-46. |
| [17] |
LIN H P, CHEN Y C, CHEN D, et al. Effect of cold deformation on the recrystallization behavior of FePd alloy at the ordering temperature using electron backscatter diffraction[J]. Materials Characterization, 2014, 94: 138-148. DOI:10.1016/j.matchar.2014.05.018 |
| [18] |
LU H, SIVAPRASAD P, DAVIES C H J. Treatment of misorientation data to determine the fraction of recrystallized grains in a partially recrystallized metal[J]. Materials Characterization, 2003, 51(5): 293-300. DOI:10.1016/j.matchar.2004.01.005 |
| [19] |
JIN Y, LIN B, BERNACKI M, et al. Annealing twin development during recrystallization and grain growth in pure nickel[J]. Materials Science and Engineering: A, 2014, 597: 295-303. DOI:10.1016/j.msea.2014.01.018 |
| [20] |
CHEN M, MA E, HEMKER K J, et al. Deformation twinning in nanocrystalline aluminum[J]. Science, 2003, 300(5623): 1275-1277. DOI:10.1126/science.1083727 |
| [21] |
GRAY G T Ⅲ. High-strain-rate deformation: mechanical behavior and deformation substructures induced[J]. Annual Review of Materials Research, 2012, 42: 285-303. DOI:10.1146/annurev-matsci-070511-155034 |
| [22] |
VENABLES J. Deformation twinning in face-centred cubic metals[J]. Philosophical Magazine, 1961, 6(63): 379-396. DOI:10.1080/14786436108235892 |
| [23] |
MISZCZYK M M, PAUL H, DRIVER J H, et al. Recrystallization nucleation in stable aluminium-base single crystals: crystallography and mechanisms[J]. Acta Materialia, 2017, 125: 109-124. DOI:10.1016/j.actamat.2016.11.054 |
| [24] |
CAHOON J R, LI Q Y, RICHARDS N L. Microstructural and processing factors influencing the formation of annealing twins[J]. Materials Science and Engineering: A, 2009, 526(1/2): 56-61. |
| [25] |
WANG W, BRISSET F, HELBERT A, et al. Influence of stored energy on twin formation during primary recrystallization[J]. Materials Science and Engineering: A, 2014, 589: 112-118. DOI:10.1016/j.msea.2013.09.071 |
| [26] |
FIELD D P, EAMES R C, LILLO T M. The role of shear stress in the formation of annealing twin boundaries in copper[J]. Scripta Materialia, 2006, 54(6): 983-986. DOI:10.1016/j.scriptamat.2005.11.037 |
| [27] |
MAHAJAN S, PANDE C, IMAM M, et al. Formation of annealing twins in fcc crystals[J]. Acta Materialia, 1997, 45(6): 2633-2638. DOI:10.1016/S1359-6454(96)00336-9 |
| [28] |
UPMANYU M, SROLOVITZ D, SHVINDLERMAN L, et al. Misorientation dependence of intrinsic grain boundary mobility: simulation and experiment[J]. Acta Materialia, 1999, 47(14): 3901-3914. DOI:10.1016/S1359-6454(99)00240-2 |
| [29] |
JIN Z H, GUMBSCH P, ALBE K, et al. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals[J]. Acta Materialia, 2008, 56(5): 1126-1135. DOI:10.1016/j.actamat.2007.11.020 |
 2021, Vol. 49
2021, Vol. 49