文章信息
- 乔及森, 孔海勇, 苗红丽, 李明
- QIAO Ji-sen, KONG Hai-yong, MIAO Hong-li, LI Ming
- 梯度铝蜂窝夹芯板的力学行为
- Mechanical behavior of gradient aluminum honeycomb sandwich panels
- 材料工程, 2021, 49(3): 167-174
- Journal of Materials Engineering, 2021, 49(3): 167-174.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.001150
-
文章历史
- 收稿日期: 2019-12-10
- 修订日期: 2020-10-22
2. 兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 兰州 730050
2. State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals, Lanzhou University of Technology, Lanzhou 730050, China
铝合金蜂窝三明治板结构,比强度和比刚度大,并具备优良的缓冲吸能特性和耐腐蚀性能,不仅在铁路车辆、汽车、地铁上得到了充分的重视,而且在飞机、船舶、航天器返回舱等领域也得到了广泛的应用[1-4]。近年来,随着工程科学的发展,尤其是高速列车时速的提升,使其在碰撞过程中需要消耗大量的动能,传统蜂窝结构的能量吸收性能已不能满足其要求,因此,创新型蜂窝结构成为人们研究的热点[5-8]。
梯度铝蜂窝夹芯结构作为创新型蜂窝结构的一种,众多学者对其进行了大量的研究。Palomba等[9]分析了不同芯层密度的双层蜂窝夹层结构,将双层板的比能量吸收与单层蜂窝板和其他轻质板相比较,通过低速冲击实验评估了它们的能量吸收能力,结果发现相同冲击能量下,双层蜂窝夹芯板的比能量吸收优于单层蜂窝夹芯板的比能量吸收。Wang等[10]通过实验和有限元模拟,研究了均匀夹芯板与分层梯度铝泡沫芯冲击载荷下的动态响应,结果表明,分层泡沫芯的密度梯度对前板的变形和破坏行为有显著影响,由有限元分析可知,导致前面板失效的临界冲击能随第一芯层密度的增加而增加,此外,通过调整前后密度比可以有效提高夹芯板的冲击性能。Tian等[11]采用有限元模拟研究了功能梯度闭孔泡沫铝芯全金属夹层板的动态响应和抗爆性能,并与单层夹芯板进行了对比,结果表明,相对于经受相同爆炸冲击加载的常规单层夹芯板,梯度分层夹芯板具有较小的中心横向偏转和优异的抗爆性。Li等[12]对爆炸载荷作用下金属夹芯板的分层梯度铝蜂窝芯的响应进行了实验研究,经研究发现,夹层板的抗爆性能对芯层相对密度和梯度分布比较敏感,在相同加载条件下,对于芯层相对密度下降排列的蜂窝夹芯板,芯层塑性能耗和传递力衰减均大于未分层的蜂窝板。Yu等[13]通过在芯中引入非均匀质量分布(梯度),利用有限元模拟系统地研究了具有线性面内芯梯度夹层板的响应,在准静态和爆破载荷情况下,发现正梯度芯层与没有梯度或具有负梯度的芯层相比在刚度,强度以及塑性能量耗散方面均表现出优势。
通过以上分析可知,众多关于分层铝蜂窝夹芯板研究主要围绕着低速冲击、高速冲击以及爆炸冲击条件下铝蜂窝的变形模式、平台应力、比吸能展开,然而对于相同质量下不同的线性梯度(梯度率)对铝蜂窝夹芯板结构能量吸收影响的研究却相对有限,针对这一问题,本工作通过实验和模拟相结合的方法对准静态以及冲击载荷作用下,不同的梯度率对蜂窝夹芯板的力学响应做了系统的研究,对比了在不同梯度率下,梯度夹芯蜂窝板的力学性能和能量吸收,为铝蜂窝夹芯板的优化设计和应用提供理论和实验指导。
1 梯度铝蜂窝板的结构设计 1.1 相对密度蜂窝结构的性能取决于其相对密度,相对密度指铝蜂窝密度与蜂窝基体密度之比[14]。不考虑环氧树脂胶层的影响,则每一个六边形铝蜂窝胞元由两个2t厚的竖(或横)边和4个t厚的斜边组成,边与边之间的夹角为120°,六边形铝蜂窝胞元的边长为L,六边形铝蜂窝拓扑结构如图 1(a),阴影部分的尺寸如图 1(b)所示。

|
图 1 铝蜂窝拓扑结构尺寸示意图 (a)铝蜂窝拓扑结构;(b)阴影部分尺寸 Fig. 1 Schematic diagram of the topology of the aluminum honeycomb (a)aluminum honeycomb topology; (b)shadow part size |
阴影部分的面积Ay:
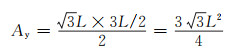
|
(1) |
式中L为铝蜂窝胞元边长尺寸。
阴影部分中铝蜂窝基体的面积Ab:
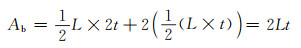
|
(2) |
式中t为铝蜂窝胞元壁厚。
假设每层铝蜂窝高度为h,铝蜂窝基体密度为ρb,铝蜂窝的密度ρy可由式(3)计算:
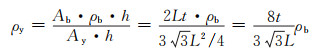
|
(3) |
铝蜂窝的相对密度可表示为:
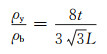
|
(4) |
由式(4)可知,铝蜂窝的相对密度仅与蜂窝胞元的边长和厚度有关。
1.2 梯度率在分层铝蜂窝夹芯板的设计中有一种是根据相邻层间的相对密度变化呈线性而进行设计出的结构形式,这种铝蜂窝结构通常被称为分段线性梯度蜂窝。到目前为止,研究人员已经对梯度系数对能量吸收的影响做了大量的实验研究,然而关于梯度率的大小对能量吸收影响的研究相对较少,借鉴文献[15]对于梯度率的定义,本工作中梯度率的公式为:

|
(5) |
式中:ρn为蜂窝板第n层的相对密度;h为第n层的高;H为试样总高度;γ为无量纲的数值,表示梯度率。
根据相对密度和梯度率式(4),(5)设计了3种不同梯度率的蜂窝夹芯板,其层级之间的关系如下:
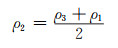
|
(6) |
在中间层蜂窝芯的相对密度一定的情况下,2ρ2≥ρ2>ρ3, ρ1≥ρ2>0, 根据GB/T 1453-2005的要求规范,对于蜂窝、波纹等格子型芯子,试样边长或直径为60 mm,或至少应包括4个完整格子,因此密度最小层级的胞元边长范围为12 mm≥Lmin≥4 mm,密度最大层级的胞元边长范围为4 mm≥Lmax≥2.4 mm,则0.0334>γ≥0。根据胞元的边长范围,本次实验选用胞元厚度为t=0.04 mm,设计了4种不同梯度率的蜂窝夹芯板,具体的设计参数如表 1所示。
| Gradient rate | Cell side length/mm | Layered relative density | Average relative density |
| γ1=0.0276 | 2.5 | 0.0246 | 0.0154 |
| 4 | 0.0154 | ||
| 10 | 0.0062 | ||
| γ2=0.0153 | 3 | 0.0205 | 0.0154 |
| 4 | 0.0154 | ||
| 6 | 0.0103 | ||
| γ3=0.0059 | 3.5 | 0.0176 | 0.0156 |
| 4 | 0.0154 | ||
| 4.5 | 0.0137 | ||
| γ4=0 | 4 | 0.0154 | 0.0154 |
| 4 | 0.0154 | ||
| 4 | 0.0154 |
本实验选用了1060铝合金材料作为面板,选用3003H18铝合金材料作为蜂窝芯层,以环氧树脂胶作为黏合剂对两种材料进行连接,其材料合金成分如表 2和表 3所示。
| Si | Fe | Cu | Mn | Zn | Al |
| 0.6 | 0.7 | 0.05-0.2 | 1.0-1.5 | 0.1 | Bal |
| Si | Fe | Cu | Mn | Zn | Mg | Ti | Al |
| ≤0.25 | 0-0.40 | ≤0.05 | ≤0.05 | ≤0.05 | ≤0.05 | ≤0.03 | Bal |
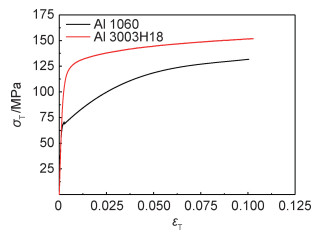
分别对两种材料进行力学性能测试。根据GB/T228.1-2010制备了1060铝合金和3003H18铝合金的拉伸试样,然后通过拉伸实验测出两种材料的应力-应变,并计算出真实应力-应变值,图 2所示为两种材料的真应力-真应变曲线。
|
图 2 拉伸试样及材料真应力-真应变曲线 Fig. 2 True stress-strain curves of tensile samples and materials |
多层梯度蜂窝夹芯板试件前后面板及中间隔板均采用1060铝合金,厚度为0.5 mm,铝蜂窝芯层材料采用3003H18铝合金,铝蜂窝芯胞孔形状为正六边形,壁厚为t=0.04 mm,芯层高度h1=h2=h3=8 mm,试样总高度H=26 mm,每级芯层所对应的铝蜂窝胞元边长L分别为:L1=3 mm,L2=4 mm,L3=6 mm。将其利用环氧树脂胶进行粘接,粘接好的夹芯板试件如图 3所示,面板及芯层的材料通过拉伸实验测得的力学性能参数如表 4所示,其中σ0.2为材料的屈服应力,E为材料的弹性模量,ρs为材料密度,ν为泊松比。

|
图 3 夹芯板试样 Fig. 3 Sample of sandwich panel |
| Materials | σ0.2/MPa | E/GPa | ρs/(g·cm-3) | ν |
| AL1060 | 66.7 | 69 | 2.7 | 0.33 |
| AL3003H18 | 123 | 69 | 2.73 | 0.33 |
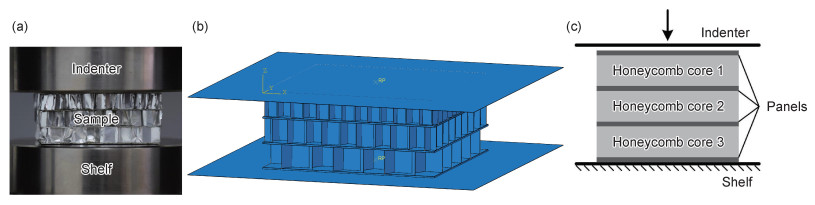
利用SHIMADZU-10TA的万能试验机对制备好的梯度夹芯板试件进行准静态压缩实验。压缩速度为2 mm/min,试件放置位置及状态如图 4(a)所示,实验过程中使用微焦照相机记录夹芯板变形过程的载荷-位移数据。
|
图 4 实验模型图 (a)试件放置;(b)有限元模型;(c)冲击装配图 Fig. 4 Experimental and model diagrams (a)specimen placement; (b)finite element model; (c)impact assembly drawing |
采用ABAQUS/EXPLICIT对实验进行准静态压缩模拟。假定各向同性并忽略应变率的影响,各部件材料属性为拉伸实验所测得的材料参数,面板使用实体单元,由于在平压过程中面板几乎无塑性变形,因此网格尺寸设置为1 mm,共3600个C3D8R个单元,六边形蜂窝芯采用壳单元计算,厚度偏移设置为中面,网格尺寸大小为0.5,共98816个S4R单元,模型尺寸为60 mm×60 mm×26 mm,蜂窝板各部件之间采用绑定约束,根据压缩实验状态,蜂窝板需置于上下压头之间,因此构造离散刚体代替试验机压头,如图 4(b)所示,上下面板与离散刚体之间的约束设为表面与表面接触,摩擦因数设为0.5,与蜂窝板下面板接触的刚体固定,与上面板接触的刚体施加位移边界条件,压缩位移设为20 mm。
根据标准EN15227-2008确定蜂窝夹芯板的高速冲击碰撞仿真情形,通过ABAQUS/EXPLICIT对冲击实验进行模拟。假定用于冲击试件的面板和芯层在冲击过程没有分离现象的发生,各部件材料属性为拉伸实验所测得的材料参数,面板选用的是实体单元,采用C3D8R的线性六面体单元,进行减缩积分和沙漏控制,网格尺寸为1 mm,蜂窝芯为壳单元,采用S4R的线性四边形单元,此类单元为四结点曲面薄壳或厚壳,减缩积分,沙漏控制,有限膜应变,网格尺寸设定为0.5 mm,面板与芯层设置成绑定约束,根据实际冲击实验状况,构造两个离散刚体代替冲击实验的冲击端压头和工作台,冲击端压头质量为5 kg,压头尺寸(长×宽)为100 mm×100 mm,给定X3方向自由度,其余方向自由度设置为0,刚体与试样之间留存0.5 mm的距离,以此来更好地还原冲击实验的实际状态,冲击端在实验过程中是在自由状态下获得一个向下的速度,虽然在实际工作中它具有加速过程,但在仿真模拟中可将其简化为具有一个初速度并以此初速度匀速向下,直到撞击到梯度蜂窝夹芯板试件,具体设定方式是在设置载荷时在预定义场中对冲击端的初始状态添加一个速度,本次实验模拟所设置的速度为50 m/s,冲击的初始能量值为6.25 kJ;工作台的刚体边界条件通过约束全部自由度来施加,刚体与工作台之间的相互关系设为表面与表面接触,摩擦因数为0.2,冲击装配图如图 4(c)所示。
3 力学性能分析 3.1 梯度蜂窝板准静态压缩性能为了确定准静态下梯度蜂窝夹芯板力学性能,分别进行了实验和数值模拟研究。图 5是在微焦摄像机下观察到的准静态压缩下面板与芯层交接处的局部放大图,通过实验研究发现在准静态压缩全程,面板与芯层之间胶接层未出现开裂,可能有以下几种原因:一是由于芯层胞壁较薄,在压缩过程中蜂窝夹芯板中芯层胞壁率先屈曲变形,对胶接层起到了缓冲卸载的作用;二是相比薄壁蜂窝铝及面板层材料,胶结层的压缩强度较高,经过压缩逐渐密实后的软金属层嵌入硬胶层之间,可以有效减缓胶层的应力集中,从而降低了胶层启裂的概率;三是压缩应力状态有利于微裂纹的闭合,抑制其扩展。

|
图 5 准静态压缩下面板与芯层交接处的局部放大图 (a)d1=8.3;(b)d2=14.8;(c)d3=20.8 Fig. 5 Partially enlarged view of the interface between the quasi-static compression lower panel and the core layer (a)d1=8.3;(b)d2=14.8;(c)d3=20.8 |
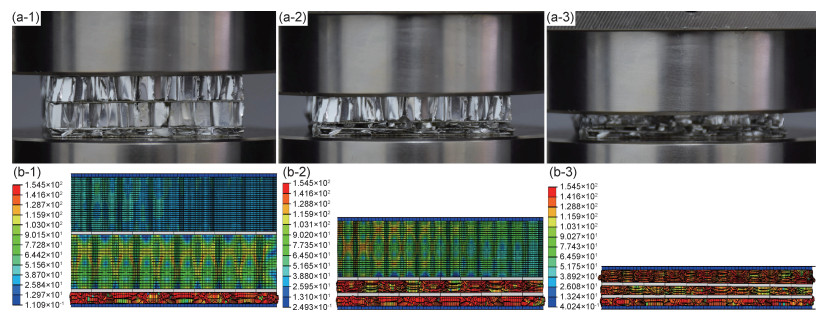
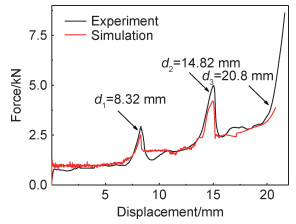
图 6为准静态下实验和模拟压缩示意图,图 7为准静态下实验和模拟的载荷-位移曲线。由图 6可以发现铝蜂窝梯度夹芯板的变形根据各蜂窝芯层密度的不同,蜂窝芯的变形顺序是从低密度向高密度逐级变形的,直至蜂窝板完全密实,另外由于在准静态压缩过程中,试件的受力较为均匀,所以蜂窝夹芯板中间的隔板基本没有发生明显的形变。根据图 7的载荷-位移曲线可以观察到曲线出现了3个密实化峰值点,所对应的位移分别是d1=8.32 mm,d2=14.82 mm,d3=20.8 mm,结合图 6可以发现,曲线出现峰值点时的位移与实验过程中试样芯层逐级密实时的位移是吻合的,说明在准静态压缩过程中,梯度蜂窝板的变形是根据芯层密度的变化而逐层变形,从另一方面也说明了蜂窝芯层密度越大,梯度蜂窝夹芯板所能承受的载荷也就越大,芯层抵抗变形的能力也就越强。另外,由各芯层密实时的压缩位移可以看出,随芯层密度的增大,各芯层的达到密实时所压缩的位移之差是逐渐减小的,根据Wierzbicki[16]的研究可知,孔壁是按波长(渐进折叠,而波长约等于蜂窝胞元边长,芯层密度是根据胞元边长的改变而变化的,而密度越大的芯层其胞元边长越小,孔壁折叠次数越多,芯层会越快速地密实化,因此,层级之间的密实化时所压缩的位移之差会逐渐变小。
|
图 6 铝蜂窝梯度夹芯板变形过程 (a)实验压缩过程;(b)模拟压缩过程; (1)d1=8.3;(2)d2=14.8;(3)d3=20.8 Fig. 6 Deformation process of aluminum honeycomb gradient sandwich panel (a)testing pressure reduction process; (b)analoging compression process; (1)d1=8.3;(2)d2=14.8;(3)d3=20.8 |
|
图 7 准静态载荷-位移曲线 Fig. 7 Quasi-static load-displacement curve |
为了确定在高速冲击载荷下梯度率对蜂窝夹芯板抗冲击性能的影响,现保持冲击速率v=50 m/s,蜂窝板总高度H=26 mm,使用4种同等质量的不同梯度率的梯度夹芯蜂窝板,即γ1=0.0276,γ2=0.0153,γ3=0.0059,γ4=0进行了相应的数值模拟。
图 8为冲击压头的载荷-位移关系,图 9为位移d=4.6 mm时γ1, γ2, γ3的试件变形图。由图 9可以观察到,在高速冲击下,梯度蜂窝板并非严格按照准静态过程中逐级变形密实,这是因为在冲击过程中,靠近冲击端的蜂窝芯层的变形主要依靠锤头的冲击惯性决定的,芯层密度起次要作用,而随着芯层的增加,锤头的冲击惯性逐渐减小,此时影响蜂窝芯层形变的是芯层密度,整块蜂窝板在锤头冲击惯性及芯层密度的相互影响下,各芯层胞壁先后发生弹性屈曲变形,随后芯层才逐渐被压溃密实,由图 8中γ1, γ2, γ3的载荷位移曲线也可以看出,梯度蜂窝板在塑性变形阶段载荷较平缓,并未出现峰值,这说明冲击过程中,在锤头冲击惯性及芯层密度的相互作用下,梯度蜂窝板的变形是整体发生的线弹性变形、弹性屈曲、塑性坍塌及密实化。同时,从图 8中还可以观察到,不同的梯度率有不同的冲击载荷峰值,载荷峰值与梯度率成正比关系,联系前面所叙述的梯度蜂窝板芯层的变形情况,可以发现冲击端芯层的密度越大,蜂窝板的冲击载荷峰值越高,蜂窝板的抗冲击性能越好。

|
图 8 不同梯度率试样冲击载荷-位移曲线 Fig. 8 Impact load-displacement curves of samples with different gradient rates |

|
图 9 试样变形图(d=4.6 mm) (a)γ1=0.0276;(b)γ2=0.0153;(c)γ3=0.0059 Fig. 9 Deformation diagram of specimen(d=4.6 mm) (a)γ1=0.0276;(b)γ2=0.0153;(c)γ3=0.0059 |
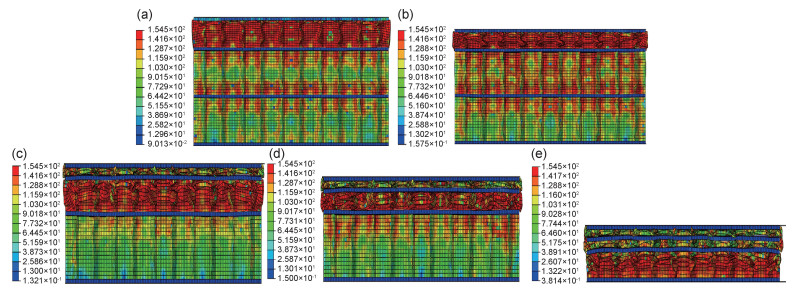
图 10中γ4的试样变形图显示当梯度率γ4=0时,由于各级芯层的密度均相同,此时分层蜂窝板的变形主要依靠冲击惯性的作用决定,而冲击惯性随冲击压头首先作用在最上层面板及最上层的蜂窝芯,因此蜂窝夹芯板的变形模式是从冲击端开始逐层变形,从图 8中也可以观察到梯度率γ4=0时,蜂窝夹芯板的载荷-位移曲线有多个密实化峰值,这也验证了在冲击过程中均质蜂窝板是从冲击端开始逐层密实的。
|
图 10 试样变形图(γ4=0) (a)d=3.2 mm; (b)d=8.5 mm; (c)d=11.6 mm; (d)d=15 mm; (e)d=18.3 mm Fig. 10 Deformation diagram of specimen(γ4=0) (a)d=3.2 mm; (b)d=8.5 mm; (c)d=11.6 mm; (d)d=15 mm; (e)d=18.3 mm |
为了确定在高速冲击载荷下梯度率对蜂窝夹芯板抗冲击性能的影响,模拟了上述同等质量的3种不同梯度率以及均质的夹芯蜂窝板,其塑性变形能随位移的变化如图 11所示。
|
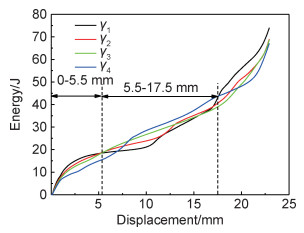
图 11 不同梯度率下夹芯蜂窝板的能量吸收 Fig. 11 Energy absorption of sandwich honeycomb panels at different gradient rates |
由图 11可以观察到,当冲击压缩位移达到5.5 mm之前,梯度蜂窝板曲线呈明显的外凸形,并且塑性变形能都要高于均匀蜂窝板,另外,当梯度率越大,曲线外凸越明显即吸能越多,这主要是因为在冲击过程中,由于受冲击惯性和芯层本身密度共同影响,因此靠近冲击端的蜂窝芯层优先变形,而能量吸收又与蜂窝芯层的塑性铰有关,根据Wierzbicki[16]的蜂窝芯孔壁折叠理论,相同高度下,蜂窝芯胞元的边长越小压缩过程中所形成的塑性铰越多,所以在塑性变形过程中芯层胞元边长越小其吸能性越好;当压缩位移大于5.5 mm之后,曲线转变为内凹状,此时均质的吸能性要优于梯度试样的吸能性,直到压缩位移至17.5 mm之后,梯度试样的吸能性又好于均匀试样,这主要是因为随着冲击过程的进行,梯度蜂窝芯层的孔壁折叠由胞元边长小的芯层延伸到胞元边长较大的芯层,在这段位移过程中,主要是由胞元边长较大的芯层所形成的塑性铰来进行能量吸收,因此均质蜂窝板此时吸能性会优于梯度蜂窝板,但随着冲击的进行,当梯度蜂窝芯胞元边长较大的芯层塑性铰形成结束后,未密实的边长较小的胞元芯层又开始形成塑性铰直至芯层完全密实,此时梯度蜂窝板的吸能性又好于均质蜂窝板。由以上分析可知,对蜂窝板进行梯度的设计可以提高其在冲击前期的能量吸收能力。
另外,蜂窝板发生变形时所需要的能量是反映其吸能性的重要指标。Zhang等[7]在研究帽形结构耐撞性问题时,提出一种表征结构碰撞过程中所需能量的方法,即
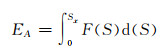
|
(7) |
式中:EA为结构冲击过程中所需要的能量;S为冲击过程中锤头的位移;F(S)为动态冲击力;Sx为动态冲击过程中蜂窝板密实化之前锤头的位移值。
通过表 5对不同梯度率的蜂窝夹芯板能量吸收情况的分析可知,当梯度率为γ1=0.0276时,梯度蜂窝夹芯板的吸能性达到最好,相较于同等质量下的均质蜂窝夹芯板,能量吸收提高了10.63%,所以同等质量下梯度蜂窝板的吸能性要优于均质蜂窝板的吸能性。
| Gradient rate | Absorbed energy/J | Energy absorption increase rate/% |
| γ1=0.0276 | 74.034 | 10.63 |
| γ2=0.0153 | 68.995 | 3.10 |
| γ3=0.0059 | 68.704 | 2.66 |
| γ4=0 | 66.922 | 0 |
(1) 在准静态压缩过程中,铝蜂窝梯度夹芯板的变形具有明显的局部化特征,蜂窝芯的变形顺序为低密度优先变形直至密实,层级之间的密实化应变差随芯层密度的增大而逐渐减小。
(2) 在高速冲击下,梯度蜂窝板并非严格按照准静态过程中逐级变形直至密实,而是在锤头冲击惯性及芯层密度的相互作用下整体发生的线弹性变形、弹性屈曲、塑性坍塌及密实化,并且不同梯度率的蜂窝板的冲击载荷峰值与冲击端芯层的密度有关,冲击端芯层的密度越大,蜂窝板的冲击载荷峰值越高,蜂窝板的抗冲击性能越好。
(3) 对蜂窝板进行梯度的设计可以提高其在冲击前期的能量吸收能力,当梯度率为γ1=0.0276时,梯度蜂窝夹芯板的吸能性达到最好,相较于同等质量下的均质蜂窝夹芯板,能量吸收提高了10.63%。
| [1] |
WANG Y, MAO H, ZUO Q, et al. Dynamic crushing and energy absorption of functionally graded aluminum cellular metal with cubic structure[C]//2016 IEEE International Conference on Information and Automation (ICIA). IEEE, 2016.
|
| [2] |
李超超, 向建华, 王慧敏. 汽车保险杠系统吸能盒结构参数对低速碰撞下吸能特性的影响[J]. 西安交通大学学报, 2017, 51(10): 77-81. LI C C, XIANG J H, WANG H M. Influence of structural parameters of energy absorbing box of automobile bumper system on energy absorption characteristics under low velocity collision[J]. Journal of Xi'an Jiaotong University, 2017, 51(10): 77-81. |
| [3] |
LI M, DENG Z, LIU R, et al. Crashworthiness design optimisation of metal honeycomb energy absorber used in lunar lander[J]. International Journal of Crashworthiness, 2011, 16(4): 411-419. DOI:10.1080/13588265.2011.596677 |
| [4] |
敬霖, 王志华. 多孔金属及其夹芯结构力学性能的研究进展[J]. 力学与实践, 2015, 37(1): 1-24. JING L, WANG Z H. Research progress on mechanical properties of porous metal and its sandwich structure[J]. Mechanics in Engineering, 2015, 37(1): 1-24. |
| [5] |
XING Y, YANG X, YANG J, et al. A theoretical model of honeycomb material arresting system for aircrafts[J]. Applied Mathematical Modelling, 2017, 48: 316-337. DOI:10.1016/j.apm.2017.04.006 |
| [6] |
QI C, SUN Y, YANG S. A comparative study on empty and foam-filled hybrid material double-hat beams under lateral impact[J]. Thin-Walled Structures, 2018, 129: 327-341. DOI:10.1016/j.tws.2018.04.018 |
| [7] |
ZHANG H, SUN G, XIAO Z, et al. Bending characteristics of top-hat structures through tailor rolled blank (TRB) process[J]. Thin-Walled Structures, 2018, 123: 420-440. DOI:10.1016/j.tws.2017.10.032 |
| [8] |
WANG Z. Recent advances in novel metallic honeycomb structure[J]. Composites: Part B, 2019, 166: 731-741. DOI:10.1016/j.compositesb.2019.02.011 |
| [9] |
PALOMBA G, EPASTO G, CRUPI V, et al. Single and double-layer honeycomb sandwich panels under impact loading[J]. International Journal of Impact Engineering, 2018, 121: 77-90. DOI:10.1016/j.ijimpeng.2018.07.013 |
| [10] |
SUN G, WANG E, WANG H, et al. Low-velocity impact behavior of sandwich panels with homogeneous and stepwise graded foam cores[J]. Materials & Design, 2018, 160: 1117-1136. |
| [11] |
LIU X R, TIAN X G, LU T J, et al. Sandwich plates with functionally graded metallic foam cores subjected to air blast loading[J]. International Journal of Mechanical Sciences, 2014, 84: 61-72. DOI:10.1016/j.ijmecsci.2014.03.021 |
| [12] |
LI S, XIN L, WANG Z, et al. Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading[J]. Composites: Part A, 2016, 80: 1-12. DOI:10.1016/j.compositesa.2015.09.025 |
| [13] |
YU B, HAN B, SU P B, et al. Graded square honeycomb as sandwich core for enhanced mechanical performance[J]. Materials & Design, 2016, 89: 642-652. |
| [14] |
王闯, 刘荣强, 邓宗全, 等. 铝蜂窝结构的冲击动力学性能的实验及数值研究[J]. 振动与冲击, 2008, 27(11): 56-61. WANG C, LIU R Q, DENG Z Q, et al. Experimental and numerical study on impact dynamic properties of aluminum honeycomb structures[J]. Journal of Vibration & Shock, 2008, 27(11): 56-61. |
| [15] |
张金山. 金属圆形蜂窝制备及其面内压缩力学性能和吸能性研究[D]. 兰州: 兰州理工大学, 2019. ZHANG J S. Fabrication of metal circular honeycomb and study on its in-plane compressive mechanical properties and energy absorption[D]. Lanzhou: Lanzhou University of Technology, 2019. |
| [16] |
WIERZBICK T. Crushing analysis of metal honeycombs[J]. International Journal of Impact Engineering, 1983, 1(2): 157-174. DOI:10.1016/0734-743X(83)90004-0 |
 2021, Vol. 49
2021, Vol. 49


