文章信息
- 乔士宾, 何西扣, 刘敬杰, 赵德利, 刘正东
- QIAO Shi-bin, HE Xi-kou, LIU Jing-jie, ZHAO De-li, LIU Zheng-dong
- SA508Gr.4N钢热变形过程微观组织演变及流变应力模型
- Microstructure evolution and flow stress modeling of SA508Gr.4N steel during hot deformation process
- 材料工程, 2021, 49(3): 67-77
- Journal of Materials Engineering, 2021, 49(3): 67-77.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000566
-
文章历史
- 收稿日期: 2020-06-23
- 修订日期: 2020-12-14
2. 天津重型装备工程研究有限公司, 天津 300457
2. Tianjin Heavy Industries Research & Development Co., Ltd., Tianjin 300457, China
金属材料热变形过程中,由于温度和变形的耦合作用,使得其内部组织会发生多种机制的变化,如热变形阶段的加工硬化、动态回复和动态再结晶(dynamic recrystallization, DRX)[1-2],热变形结束后的静态再结晶和亚动态再结晶[3-5]。其中,动态再结晶对金属材料内部微观组织的变化起着至关重要的作用。掌握金属材料高温变形行为对工业过程的数值模拟具有重要意义,通过数值模拟技术成功地对热加工过程进行建模的前提是精确建立用于描述应变、应变速率、温度等对流变应力与微观组织影响规律的模型。近年来,基于实验室数据对金属材料流变应力和微观组织演变模型进行了大量的研究[6-8]。
SA508Gr.4N钢相比目前广泛应用于核电压力容器的SA508Gr.3钢,具有更高的强度和更好的低温韧性,所以将其作为核电压力容器大锻件用钢的新一代材料。许多学者对SA508Gr.4N钢进行了多方面的研究。刘宁等[9]研究了预备热处理工艺对消除粗大晶粒组织遗传性的影响。Yang等[10]研究了SA508Gr.4N钢微观组织对冲击韧性和回火脆性的影响。Park等[11]研究了Ni, Cr, Mo元素对Ni-Mo-Cr系低合金钢微观组织和力学性能的影响。SA508Gr.4N钢属于Ni-Cr-Mo系低合金钢,具有严重的粗大晶粒组织遗传性,不合理的锻造方式会造成锻件出现混晶,并且混晶组织通过后续热处理是很难消除的。因此,通过建立SA508Gr.4N钢的流变应力模型和微观组织演变模型为大锻件的有限元模拟及工业锻造提供理论基础数据,进而优选出最佳的锻造工艺,使锻件内部获得细小、均匀的等轴晶组织[12-14]。
本工作对SA508Gr.4N钢进行了等温热压缩实验,系统研究了变形温度和应变速率对流变应力与微观组织的影响。在实验结果的基础上,建立了基于物象的两阶段流变应力模型(包括动态回复和动态再结晶)和动态再结晶晶粒尺寸模型,并验证了模型准确性。
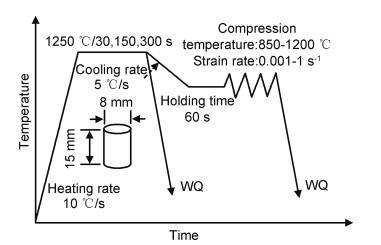
1 实验材料与方法实验用SA508Gr.4N钢的化学成分如表 1所示。单道次热压缩实验在Gleeble-1500D热模拟试验机上进行。为了降低工件与压头之间的摩擦,减小不均匀变形同时避免变形后工件焊接到压头之上,在压头与工件之间放置了厚度为0.5 mm的钽片。试样以10 ℃/s的加热速率加热到1250 ℃,然后保温300 s,再以5 ℃/s的速率降至设定的热变形温度,将试样保温60 s以确保实验在恒温下进行,所有试样以0.9真应变热压缩结束后,立即水淬以保留变形后的奥氏体晶粒形貌。热变形温度分别为850, 950, 1050, 1150, 1200 ℃,变形速率分别为0.001, 0.01, 0.1, 1 s-1,如图 1所示。
| C | Si | Mn | Ni | Cr | Mo | P | S | Al | Fe |
| 0.17 | 0.015 | 0.35 | 3.71 | 1.69 | 0.51 | 0.0016 | 0.0018 | 0.030 | Bal |
|
图 1 热压缩变形工艺图 Fig. 1 Scheme of hot compression process |
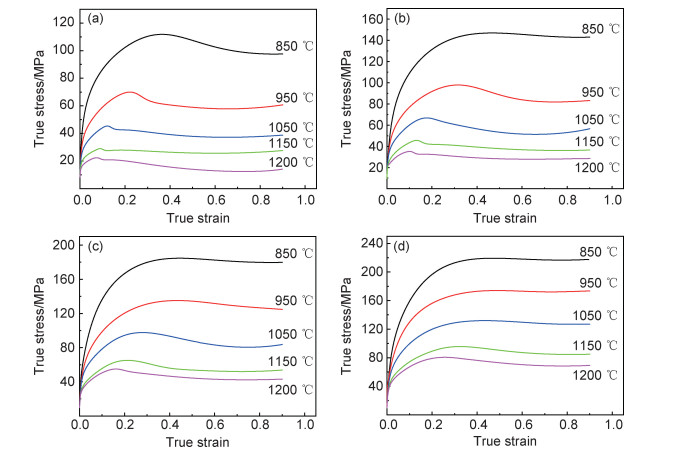
SA508Gr.4N钢在不同实验条件下的流变应力曲线如图 2所示。初始阶段由于加工硬化的影响,应力快速增加;真应变超过临界应变后,由于动态再结晶和动态回复的作用,使得流变应力增加幅度降低,直到达到峰值应力(σp);当软化速率大于加工硬化速率时,应力开始下降,在软化速率和加工硬化速率达到新的动态平衡时,应力进入稳态阶段。由图 2可知,所有的流变应力曲线都表现为达到峰值应力后,逐渐降到稳态应力,这说明SA508Gr.4N钢在变形温度为850~1200 ℃、应变速率为0.001~1 s-1条件下的流变应力曲线表现为典型的动态再结晶型。随着变形温度的增加和应变速率的降低,峰值应力和峰值应变(εp)逐渐降低。在相同真应变量下,当温度一定时,随着应变速率的增加,变形时间缩短,将导致在短时间内位错密度急剧增加,增强了加工硬化效果,同时由于变形时间的缩短,降低了动态回复和动态再结晶的软化作用,二者同时作用使得变形抗力增大,流变应力增加[15-16];而当应变速率不变时,随着变形温度的升高,增强了原子的热激活作用,加速了位错运动,使得位错滑移阻力降低,从而导致流变应力下降[17]。
|
图 2 不同变形条件下SA508Gr.4N钢的真应力-真应变曲线 (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 Fig. 2 True stress-true strain curves of SA508Gr.4N steel under different deformation conditions (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 |
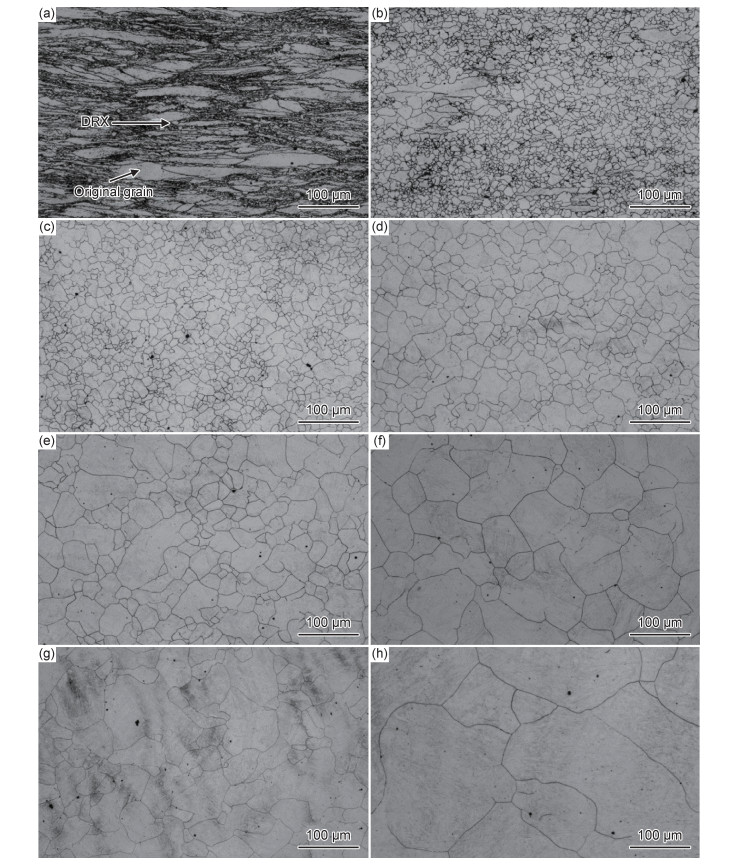
当真应变量为0.9时,变形温度和应变速率对SA508Gr.4N钢发生动态再结晶后的微观组织影响如图 3所示。从图 3(a)~(e)可知,当变形温度为850 ℃时仅发生部分动态再结晶(partial dynamic recrystallization, PDRX),且动态再结晶形成于原始晶粒的晶界处,最终形成项链状组织。随着变形温度的升高,动态再结晶体积分数逐渐增加,到1050 ℃以后,材料内部的组织已经被动态再结晶组织完全替代。随着变形温度的进一步升高,晶粒尺寸逐渐增加。当温度为1050, 1150 ℃和1200 ℃时,再结晶晶粒尺寸分别为11.48, 24.09 μm和29.50 μm。其主要原因是,随着变形温度的升高,有利于降低晶体缺陷密度从而降低储能,使动态再结晶的形核速率和动态再结晶体积分数逐渐增加;且由于变形温度的升高使界面能降低,导致动态再结晶的晶粒尺寸逐渐增大。
|
图 3 真应变为0.9时不同变形条件下SA508Gr.4N钢的晶粒微观组织 (a)850 ℃, 1 s-1; (b)950 ℃, 1 s-1; (c)1050 ℃, 1 s-1; (d)1150 ℃, 1 s-1; (e)1200 ℃, 1 s-1; (f)1200 ℃, 0.1 s-1; (g)1200 ℃, 0.01 s-1; (h)1200 ℃, 0.001 s-1 Fig. 3 Grain microstructures of SA508Gr.4N steel under different deformation conditions with the true strain of 0.9 (a)850 ℃, 1 s-1; (b)950 ℃, 1 s-1; (c)1050 ℃, 1 s-1; (d)1150 ℃, 1 s-1; (e)1200 ℃, 1 s-1; (f)1200 ℃, 0.1 s-1; (g)1200 ℃, 0.01 s-1; (h)1200 ℃, 0.001 s-1 |
从图 3(e)~(h)可知,随变形速率的降低,动态再结晶的平均晶粒尺寸逐渐增加。当变形速率为1, 0.1, 0.01 s-1和0.001 s-1时,再结晶晶粒尺寸分别为29.50, 65.15, 108.16 μm和190.05 μm。造成这种现象的主要原因包括以下两方面:一方面为应变速率的增加,变形组织中存储更多的形变能,这将增大变形组织中的位错密度和形核点位,使得再结晶后的晶粒尺寸更加细小;另一方面为应变速率增加,使得相同变形量下的变形时间缩短,再结晶后的新晶粒来不及长大,从而也造成了晶粒尺寸的降低[18]。
表 2为不同变形工艺下SA508Gr.4N钢的动态再结晶晶粒尺寸统计。由表 2可知,为满足大锻件SA508Gr.4N钢的晶粒度要求(平均晶粒尺寸≥5级,平均截距≤56.6 μm),锻造工艺应选择在以下范围内:变形温度1200 ℃,应变速率1 s-1;变形温度1150 ℃,应变速率0.1~1 s-1;变形温度950~1050 ℃,应变速率0.001~1 s-1;变形温度850 ℃,应变速率0.001 s-1。锻造结束后,内部无粗大晶粒组织,可避免SA508Gr.4N钢的粗大晶粒组织遗传性,为后续热处理提供均匀的组织,提高大锻件的组织及力学性能均匀性。
| Strain rate/s-1 | Compression temperature | ||||
| 850 ℃ | 950 ℃ | 1050 ℃ | 1150 ℃ | 1200 ℃ | |
| 0.001 | 9.84 | 25.50 | 56.43 | 116.97 | 190.05 |
| 0.01 | PDRX | 14.03 | 31.05 | 59.99 | 108.16 |
| 0.1 | PDRX | 10.02 | 21.62 | 45.13 | 65.15 |
| 1 | PDRX | 6.11 | 11.48 | 24.09 | 29.50 |
根据变形过程的微观组织机制,加工硬化和动态回复可用位错密度的演化来表示,如式(1)所示[1]:
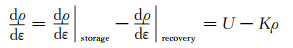
|
(1) |
式中:

|
(2) |
式中ρ0为初始位错密度。在高温状态下,位错密度的平方根与流变应力呈线性关系[19]:
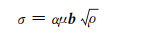
|
(3) |
式中:α为位错交互作用系数,对大多数金属而言,通常取0.5;μ为剪切模量;b为柏氏矢量。将式(3)结合式(1)进行积分,得到在动态回复阶段的流变应力(σDRV)表达式:
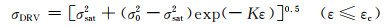
|
(4) |
式中:σsat为饱和应力,且

通常认为动态再结晶体积分数与应变量的关系可由Johnson-Mehl-Avrami-Kolmogorov(JMAK)方程表示[15],如式(5), (6)所示。

|
(6) |
式中:XDRX为动态再结晶体积分数;β,k1,a,m1均为材料常数;Q1为动态再结晶50%时的激活能。
此外,动态再结晶体积分数还可由真应力-真应变曲线获得,其表达式如下[20]:

|
(7) |
结合式(5), (7)可得动态再结晶阶段的流变应力(σDRX)模型,如式(8)所示:

|
(8) |
式中σss为稳态应力。
2.3.1 动态再结晶特征点的确定热变形过程中,通常认为只有达到临界应变(εc)以后才能发生动态再结晶[21]。临界应力可以通过加工硬化率与真应力-真应变曲线获得。
加工硬化率θ可由式(9)获得:
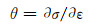
|
(9) |
不同热变形条件下SA508Gr.4N钢的加工硬化曲线如图 4所示。动态再结晶的临界应力(σc)可以利用Poliak和Jonas[22]提出的通过达到峰值应力之前的加工硬化曲线的拐点的方法计算得出,之后根据真应力-真应变曲线得出临界应变,具体公式如下:
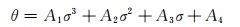
|
(10) |

|
图 4 不同热变形参数下SA508Gr.4N钢的加工硬化曲线 (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 Fig. 4 Work hardening curves for SA508Gr.4N steel under different hot deformation parameters (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 |
式中:A1,A2,A3,A4在恒定变形条件下都为常数,将式(10)两边对σ的偏导可得:
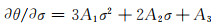
|
(11) |
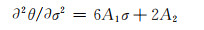
|
(12) |
θ-σ曲线的二次偏导的最小值即为临界应力(σc)。当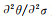
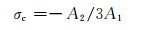
|
(13) |
将式(13)代入式(11)可以得出临界加工硬化率即为:
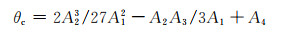
|
(14) |
如图 4(a)所示,饱和应力(σsat)是加工硬化曲线在点(θc, σc)处切线的延长线与θ=0的交点,如式(15)所示。峰值应力(σp)和稳态应力(σss)分别为θ-σ曲线上,加工硬化值为0时的两个值。根据以上方法可求出不同变形条件下的特征值。
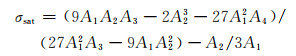
|
(15) |
金属材料热变形过程中广泛应用Arrhenius方程来描述流变应力与应变速率、变形温度的关系[23]。
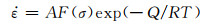
|
(16) |
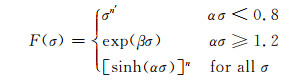
|
(17) |
式中:F(σ)为流变应力相关的函数,在不同的应力水平下,F(σ)有如式(17)所示三种表现形式;σ为流变应力,MPa;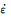
温度与应变速率对热变形行为的影响也可以用Zener-Hollomon参数(Z)表示。峰值应力σp和Z参数的关系通常如式(18)所示:

|
(18) |
图 5为SA508Gr.4N钢不同变形条件下峰值应力、变形温度与应变速率之间的关系。为了确定上述参数,将式(16), (17), (18)两边取自然对数可得到如图 5(a)和图 5(b)所示的应变速率与峰值应力的关系以及图 5(c)和图 5(d)所示的ln[sinh (ασp)]与应变速率和温度的关系。图 5表明,

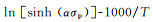

|
(19) |
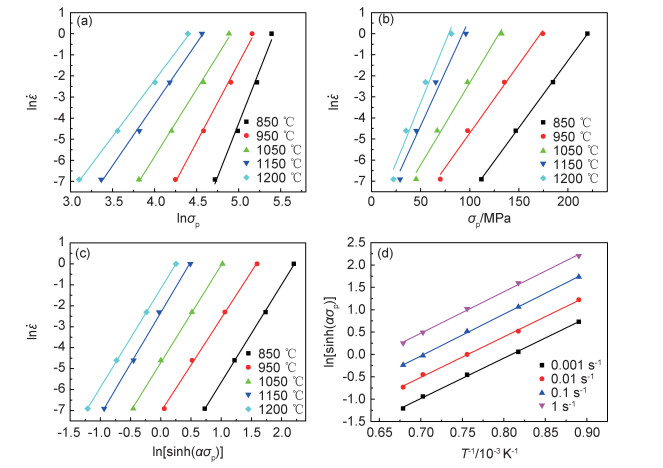
|
图 5 峰值应力、变形温度和应变速率之间的关系 (a)ln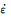 -lnσp; (b)ln -lnσp; (b)ln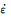 -σp; (c)ln -σp; (c)ln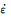 -ln [sinh (ασp)]; (d)ln [sinh (ασp)]-1000/T Fig. 5 Relationship between peak stress, deformation temperature and strain rate (a)ln -ln [sinh (ασp)]; (d)ln [sinh (ασp)]-1000/T Fig. 5 Relationship between peak stress, deformation temperature and strain rate (a)ln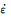 -lnσp; (b)ln -lnσp; (b)ln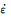 -σp; (c)ln -σp; (c)ln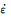 -ln [sinh (ασp)]; (d)ln [sinh (ασp)]-1000/T -ln [sinh (ασp)]; (d)ln [sinh (ασp)]-1000/T |
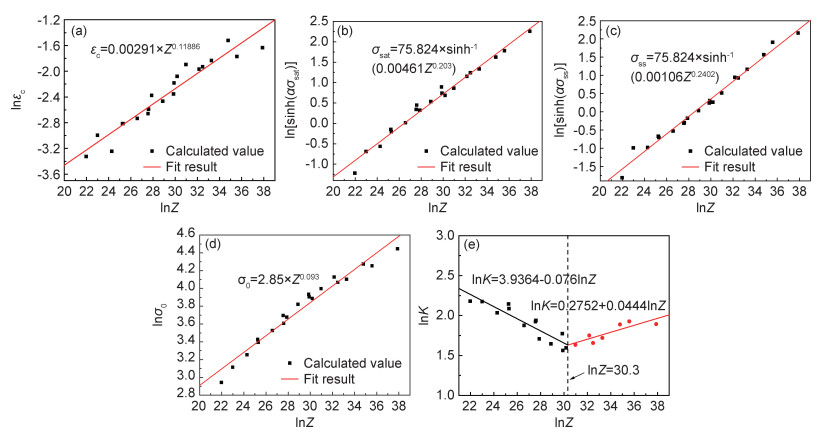
为了更加方便地表示特征值(临界应变、饱和应力、稳态应力、屈服应力),分别将lnεc, ln[sinh(ασsat)], ln[sinh(ασss)], lnσ0与lnZ作图,如图 6所示。通过图 6的线性拟合关系,εc, σsat, σss, σ0分别可以由Zener-Hollomon参数(Z)表示,如式(20)~(23)所示。将特征值代入式(4)可得出不同变形温度和变形速率下的K值,然后将lnK与lnZ作图,如图 6(e)所示,其表达式如式(24)所示。

|
(20) |
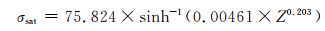
|
(21) |

|
(22) |

|
(23) |
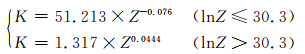
|
(24) |
|
图 6 特征值与lnZ的关系 (a)lnεc-lnZ; (b)ln[sinh(ασsat)]-lnZ; (c)ln[sinh(ασss)]-lnZ; (d)lnσ0-lnZ; (e)lnK-lnZ Fig. 6 Relationship between the characteristic value and lnZ (a)lnεc-lnZ; (b)ln[sinh(ασsat)]-lnZ; (c)ln[sinh(ασss)]-lnZ; (d)lnσ0-lnZ; (e)lnK-lnZ |
根据式(7)可计算出不同变形条件下的动态再结晶体积分数,可得动态再结晶体积分数为50%(ε0.5)时的真应变,如表 3所示。
| Strain rate/s-1 | Deformation temperature | ||||
| 850 ℃ | 950 ℃ | 1050 ℃ | 1150 ℃ | 1200 ℃ | |
| 0.001 | 0.47 | 0.29 | 0.21 | 0.15 | 0.09 |
| 0.01 | 0.55 | 0.41 | 0.25 | 0.22 | 0.17 |
| 0.1 | 0.84 | 0.54 | 0.39 | 0.31 | 0.23 |
| 1 | 0.60 | 0.51 | 0.45 | 0.35 | |
将式(6)两边取对数可得:
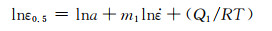
|
(25) |
将lnε0.5分别与ln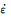

|
图 7 lnε0.5与ln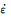 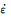 ; (b)lnε0.5-1000T-1
Fig. 7 Relationship between lnε0.5 and ln ; (b)lnε0.5-1000T-1
Fig. 7 Relationship between lnε0.5 and ln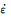 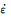 ; (b)lnε0.5-1000T-1 ; (b)lnε0.5-1000T-1
|
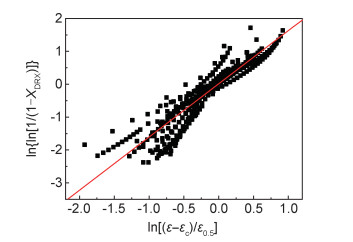
将式(5)两边取两次对数可得式(26),并将ε0.5的预测值和动态再结晶的计算值代入式(26),同时绘制图 8,经线性回归可得β为1.125,k1为1.618。
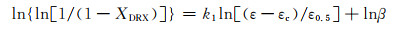
|
(26) |
|
图 8 ln{ln[1/(1-XDRX)]}和ln[(ε-εc)/ε0.5]之间的关系 Fig. 8 Relationship between ln{ln[1/(1-XDRX)]} and ln[(ε-εc)/ε0.5] |
|
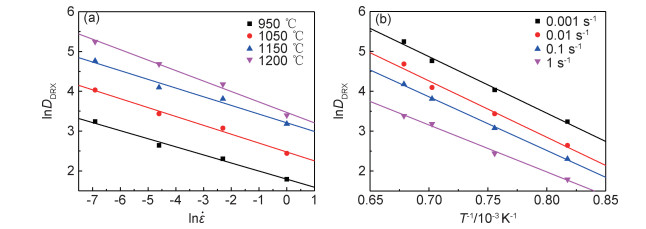
图 9 晶粒尺寸与应变速率和变形温度的线性拟合关系 (a)lnDDRX-ln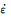 ; (b)lnDDRX-1000T-1
Fig. 9 Linear fitting relationship between grain size and strain rate, deformation temperature (a)lnDDRX-ln ; (b)lnDDRX-1000T-1
Fig. 9 Linear fitting relationship between grain size and strain rate, deformation temperature (a)lnDDRX-ln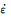 ; (b)lnDDRX-1000T-1 ; (b)lnDDRX-1000T-1
|
将所得特征值k1,a,h,Q1代入式(5)和式(6)可得SA508Gr.4N钢的动态再结晶体积分数方程,如式(27)所示:
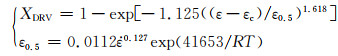
|
(27) |
因此,SA508Gr.4N钢的基于物象的流变应力本构方程可描述为:

|
(28) |
其中,σsat=75.824×sinh-1(0.00461×Z0.203);σss=75.824×sinh-1(0.00106×Z0.240);σ0=2.131×Z0.1046;εc=2.85×Z0.093;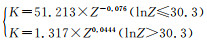
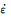
根据上述研究发现,发生完全动态再结晶后的晶粒尺寸主要受变形温度和应变速率的影响,初始晶粒尺寸影响较小。完全动态再结晶晶粒尺寸可由式(29)表示[24]。将式(29)两边取对数可得式(30),将统计后的动态再结晶晶粒尺寸、应变速率和变形温度代入式(30)可得出如图(9)所示lnDDRX-ln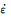
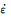
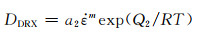
|
(29) |
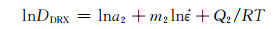
|
(30) |
式中:DDRX为动态再结晶晶粒尺寸,μm;a2, m为材料常数;Q2为晶界扩散激活能,J/mol。
综上所述,SA508Gr.4N钢的动态再结晶晶粒尺寸模型为:
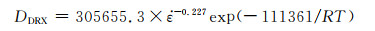
|
(31) |
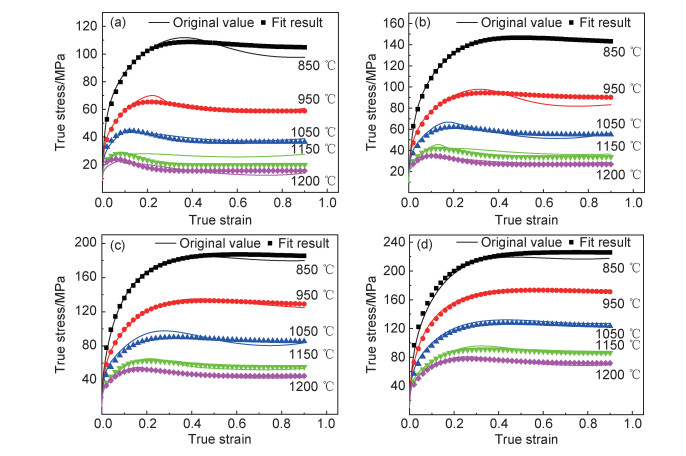
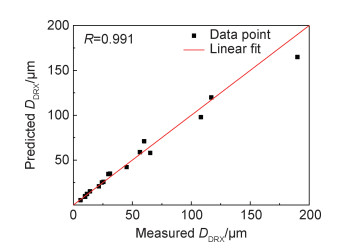
分别取真应变量0.02~0.9(共45个应变量),来验证基于物象的两阶段流变应力模型及动态再结晶晶粒尺寸模型的准确性。图 10和图 11分别为不同变形条件下的流变应力和动态再结晶晶粒尺寸的实验值与预测值对比,结果显示,流变应力预测相关系数(R)及平均相对误差(mean relative error, MRE)分别为0.998和4.76%,动态再结晶晶粒尺寸预测相关系数(R)及平均相对误差(MRE)分别为0.991和8.69%。可见该模型能较为准确地预测热变形过程中的流变应力和动态再结晶晶粒尺寸,对SA508Gr.4N钢的锻造工艺制定具有重要的参考价值。
|
图 10 不同应变速率下变形温度为850~1200 ℃时的流变应力预测值与实验值对比 (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 Fig. 10 Comparison of predicted and experimental flow stress at deformation temperature of 850-1200 ℃ under different strain rates (a)0.001 s-1; (b)0.01 s-1; (c)0.1 s-1; (d)1 s-1 |
|
图 11 不同变形条件下动态再结晶晶粒尺寸预测值与实验值对比 Fig. 11 Comparison of predicted and experimental dynamic recrystallization grain size under different deformation conditions |
(1) SA508Gr.4N钢在变形温度为850~1200 ℃、应变速率为0.001~1 s-1条件下的高温流变应力曲线为典型的动态再结晶型,随着变形温度的增加和应变速率的降低,再结晶体积分数和晶粒尺寸逐渐增加。避免粗大晶粒组织遗传性的锻造工艺为:变形温度1200 ℃,应变速率1 s-1;变形温度1150 ℃,应变速率0.1~1 s-1;变形温度950~1050 ℃,应变速率0.001~1 s-1;变形温度850 ℃,应变速率0.001 s-1。
(2) SA508Gr.4N钢基于物象的高温流变应力模型可表示为:

|
其中,σsat=75.824×sinh-1(0.00461×Z0.203); σss=75.824×sinh-1(0.00106×Z0.240); σ0=2.131×Z0.1046; εc=2.85×Z0.093; 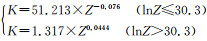
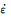
(3) SA508Gr.4N钢的动态再结晶晶粒尺寸模型可表示为:DDRX=305655.3×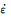
(4) 通过实验值和模型预测值对比可得:流变应力预测相关系数(R)及平均相对误差(MRE)分别为0.998和4.76%;动态再结晶晶粒尺寸预测相关系数(R)及平均相对误差(MRE)分别为0.991和8.69%。
| [1] |
王梦寒, 王根田, 王瑞, 等. Mn-Ni-Mo系核电用钢高温流变行为及热加工图[J]. 中南大学学报(自然科学版), 2017, 48(3): 592-600. WANG M H, WANG G T, WANG R, et al. Hot deformation and processing map of Mn-Ni-Mo system nuclear power steel[J]. Journal of Central South University (Science and Technology), 2017, 48(3): 592-600. |
| [2] |
DONG D Q, CHEN F, CUI Z S. A physically-based constitutive model for SA508-Ⅲ steel: modeling and experimental verification[J]. Materials Science and Engineering: A, 2015, 634: 103-115. DOI:10.1016/j.msea.2015.03.036 |
| [3] |
LI L X, ZHENG L Y, YE B, et al. Metadynamic and static recrystallization softening behavior of a bainite steel[J]. Metals and Materials International, 2018, 24(1): 60-66. DOI:10.1007/s12540-017-7201-z |
| [4] |
DONG D Q, CHEN F, CUI Z S. Investigation on metadynamic recrystallization behavior in SA508-Ⅲ steel during hot deformation[J]. Journal of Manufacturing Processes, 2017, 29: 18-28. DOI:10.1016/j.jmapro.2017.07.008 |
| [5] |
ZHOU P, MA Q X. Static recrystallization behavior of 25CrMo4 mirror plate steel during two-pass hot deformation[J]. Journal of Iron and Steel Research, International, 2017, 24(2): 222-228. DOI:10.1016/S1006-706X(17)30031-6 |
| [6] |
程明阳, 郝世明, 谢敬佩, 等. SiCP/Al-Cu复合材料的高温热变形行为[J]. 材料工程, 2017, 45(2): 17-23. CHENG M Y, HAO S M, XIE J P, et al. Hot deformation behavior of SiCP/Al-Cu composite[J]. Journal of Materials Engineering, 2017, 45(2): 17-23. |
| [7] |
张施琦, 冯定, 张跃, 等. 新型超高强度热冲压用钢的热变形行为及本构关系[J]. 材料工程, 2016, 44(5): 15-21. ZHANG S Q, FENG D, ZHANG Y, et al. Hot deformation behavior and constitutive model of advanced ultra-high strength hot stamping steel[J]. Journal of Materials Engineering, 2016, 44(5): 15-21. DOI:10.3969/j.issn.1673-1433.2016.05.004 |
| [8] |
SUI D S, WANG T, ZHU L L, et al. Mathematical modeling of high-temperature constitutive equations and hot processing maps for as-cast SA508-3 steel[J]. Journal of Metals, 2016, 68(11): 2944-2951. DOI:10.1007/s11837-016-2074-z |
| [9] |
刘宁, 刘正东, 何西扣, 等. 核压力容器用SA508Gr.4N钢组织遗传性的消除[J]. 钢铁研究学报, 2017, 29(5): 402-410. LIU N, LIU Z D, HE X K, et al. Structure inheritance removing of SA508Gr.4N steel for nuclear reactor pressure vessels[J]. Journal of Iron and Steel Research, 2017, 29(5): 402-410. |
| [10] |
YANG Z Q, LIU Z D, HE X K, et al. Effect of microstructure on the impact toughness and temper embrittlement of SA508Gr.4N steel for advanced pressure vessel materials[J]. Scientific Reports, 2018, 8(1): 207-218. DOI:10.1038/s41598-017-18434-3 |
| [11] |
PARK S G, KIM M C, LEE B S, et al. Correlation of the thermodynamic calculation and the experimental observation of Ni-Mo-Cr low alloy steel changing Ni, Mo, and Cr contents[J]. Journal of Nuclear Materials, 2010, 407(2): 126-135. DOI:10.1016/j.jnucmat.2010.09.004 |
| [12] |
TAKU S, ANDREY B, RUSTAM K, et al. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions[J]. Progress in Materials Science, 2014, 60: 130-207. DOI:10.1016/j.pmatsci.2013.09.002 |
| [13] |
WU C, HAN S. Hot deformation behavior and dynamic recrystallization characteristics in a low-alloy high-strength Ni-Cr-Mo-V steel[J]. Acta Metallurgica Sinica, 2018, 31: 963-974. |
| [14] |
朱鸿昌, 罗军明, 朱知寿. TB17钛合金β相区动态再结晶行为及转变机理[J]. 材料工程, 2020, 48(2): 108-113. ZHU H C, LUO J M, ZHU Z S. Dynamic recrystallization behavior and transformation mechanism in β-phase region of TB17 titanium alloy[J]. Journal of Materials Engineering, 2020, 48(2): 108-113. |
| [15] |
XU Y K, BIRNBAUM P, PILZ S, et al. Investigation of constitutive relationship and dynamic recrystallization behavior of 22MnB5 during hot deformation[J]. Results in Physics, 2019, 14: 102426. DOI:10.1016/j.rinp.2019.102426 |
| [16] |
HAN Y, YAN S, YIN B G, et al. Effects of temperature and strain rate on the dynamic recrystallization of a medium-high-carbon high-silicon bainitic steel during hot deformation[J]. Vacuum, 2018, 148: 78-87. DOI:10.1016/j.vacuum.2017.11.007 |
| [17] |
包喜荣, 王均安, 王晓东, 等. 一种Cr-Mo-Ni系贝氏体钢的动态再结晶行为[J]. 材料热处理学报, 2016, 37(4): 222-227. BAO X R, WANG J A, WANG X D, et al. Dynamic recrystallization behavior of Cr-Mo-Ni bainitic steel[J]. Transactions of Materials and Heat Treatment, 2016, 37(4): 222-227. |
| [18] |
CHEN X M, LIN Y C, WEN D X, et al. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation[J]. Materials & Design, 2014, 57: 568-577. |
| [19] |
DING R, GUO Z X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization[J]. Acta Materialia, 2001, 49(16): 3163-3175. DOI:10.1016/S1359-6454(01)00233-6 |
| [20] |
CHEN G J, CHEN L, ZHAO G Q, et al. Microstructure analysis of an Al-Zn-Mg alloy during porthole die extrusion based on modeling of constitutive equation and dynamic recrystallization[J]. Journal of Alloys and Compounds, 2017, 710: 80-91. DOI:10.1016/j.jallcom.2017.03.240 |
| [21] |
杨志强, 刘正东, 何西扣, 等. 反应堆压力容器用SA508Gr.4N钢的热变形行为[J]. 材料工程, 2017, 45(8): 88-95. YANG Z Q, LIU Z D, HE X K, et al. Hot deformation behavior of SA508Gr.4N steel for reactor pressure vessels[J]. Journal of Materials Engineering, 2017, 45(8): 88-95. |
| [22] |
POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1): 127-136. DOI:10.1016/1359-6454(95)00146-7 |
| [23] |
LIU N, LIU Z D, HE X K, et al. Hot deformation behavior of SA508Gr.4N steel for nuclear reactor pressure vessels[J]. Journal of Iron and Steel Research, International, 2016, 23(12): 1342-1348. DOI:10.1016/S1006-706X(16)30197-2 |
| [24] |
杨晓雅, 何岸, 谢甘霖, 等. 核电用奥氏体不锈钢的动态再结晶行为[J]. 工程科学学报, 2015, 37(11): 1447-1455. YANG X Y, HE A, XIE G L, et al. Dynamic recrystallization behavior of an austenitic stainless steel for nuclear power plants[J]. Chinese Journal of Engineering, 2015, 37(11): 1447-1455. |
 2021, Vol. 49
2021, Vol. 49


