文章信息
- 虞兮凡, 赵伶玲
- YU Xi-fan, ZHAO Ling-ling
- 热电材料β-Cu2-xSe热传导性能模拟研究
- Simulation research on thermal conductivity of thermoelectric material β-Cu2-xSe
- 材料工程, 2021, 49(2): 121-126
- Journal of Materials Engineering, 2021, 49(2): 121-126.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000077
-
文章历史
- 收稿日期: 2020-02-01
- 修订日期: 2020-05-15
热电材料利用塞贝克效应和帕尔贴效应以实现热能和电能之间的直接相互转化,在工业余热发电、热电制冷、太阳能综合利用等领域具有广泛而重要的应用前景[1-2]。研究表明[3-4],材料热电转换效率的提高依赖于热电优值[5]相关物理特性的综合提高,需要在提高电输运能力的同时降低材料的导热系数。一类新型的热电材料—“声子液体”材料[6]内含固定的亚晶格框架,可提供良好的电输运通道,同时在晶体内部又存在其他类“液态”离子可强烈散射声子,降低材料的晶格热导率,实现了热传导和电输运的协同优化。因此,研究“声子液体”热电材料的类“液态”结构特殊性,并分析该特殊性对材料热传导性能的影响,可以为热电转换效率的提高和热传导过程机理的理解提供借鉴与指导。
“声子液体”热电材料的结构特殊性在于其中包含的类“液态”离子。Liu等[7]发现Cu2-xSe晶体随着温度的升高会经历结构的相变过程,即由低温的非立方相(α相)转变为高温的立方相(β相)。在高温立方相(下文称β-Cu2-xSe)中Cu+不再有序排列,成为可迁移扩散的快离子,构成了类“液态”的亚晶格结构,而其具有的强烈散射声子能力使得Cu2-xSe晶体在高温下具有极低的热导率。Ouyang等[8]和Liang[9]分别研究了Ag2Te和Cu2S两种“声子液体”热电材料,发现这些材料中存在的类“液态”离子同样可以散射声子,降低材料的热导率,进一步验证了“声子液体”类热电材料的结构特征和优异性能。此外,Kim等[10]应用第一性原理的方法对β-Cu2-xSe的导热过程进行机理性研究,计算材料在热传导过程中的声子传输性质,尝试解释其较低热导率产生的原因。然而,目前研究更多关注“声子液体”材料的结构性质,未能深入探讨类“液态”离子对材料导热性能的影响。此外,掺杂和空位是优化材料热电性能的常用手段,然而目前对此类材料处理手段的研究鲜见报道。
本工作采用分子动力学模拟的方法研究压强为0.1 MPa,温度为500~1000 K下β-Cu2-xSe的热传导性能和扩散特性,通过计算材料的扩散系数D、导热系数k和声子输运特征,分析“声子液体”材料中类“液态”离子对导热系数的相关性,同时探讨掺杂和空位对材料导热系数所造成的影响,并解释其影响机制。
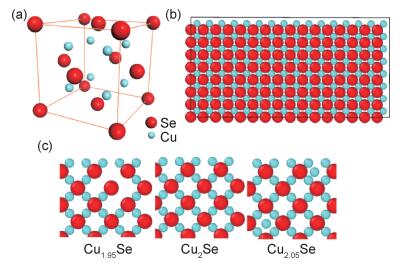
1 模型建构及研究方法 1.1 模拟方法及模型构建本工作的研究对象为β-Cu2-xSe,一种典型的“声子液体”热电材料。β-Cu2-xSe具有反萤火石结构,Se2-形成相对稳定面心立方亚晶格网络结构,Cu+则分布在硒亚晶格框架的间隙空间,同时具有随机迁移特性,其结构示于图 1。为了消除尺寸因素对导热系数计算的影响,构建2.3 nm ×2.3 nm ×4.6 nm的计算域,包含128个β-Cu2Se晶胞,共计1536个原子。此外,通过随机增添和删减Cu+的手段反映掺杂(β-Cu2.05Se)和空位(β-Cu1.95Se)对材料在微观层面上所做出的改变。
|
图 1 β-Cu2-xSe结构示意图(红色:Cu; 绿蓝色:Se) (a)β-Cu2Se的单胞结构;(b)β-Cu2Se系统的YZ平面; (c)β-Cu1.95Se,β-Cu2Se和β-Cu2.05Se的微观结构 Fig. 1 Crystal structure of β-Cu2-xSe(red: Cu; turquoise: Se) (a)unit cell of β-Cu2Se; (b)YZ plane of the β-Cu2Se system; (c)micro structure of β-Cu1.95Se, β-Cu2Se and β-Cu2.05Se |
β-Cu2-xSe中的铜和硒均为金属原子,故粒子间相互作用势能函数采用莫尔斯势[11]进行描述,莫尔斯势广泛应用于计算金属化合物的导热系数,具有良好的计算精度。莫尔斯势可化简为:
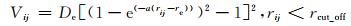
|
(1) |
式中:Vij为粒子间势能函数;De为势能阱深度;a为控制势阱的宽度参数;rij为粒子间的距离;re表示平衡时的粒子对键长;rcut_off为截断半径。
模拟采用Namsani等[12]拟合的莫尔斯势参数,示于表 1。
| Pair | De/eV | a/nm | re/nm | rcut_off/nm |
| Cu-Se | 0.1517 | 0.1391 | 0.300 | 0.35 |
| Cu-Cu | 0.4370 | 0.3034 | 0.244 | 0.35 |
| Se-Se | 0.9745 | 0.0605 | 0.468 | 0.45 |
考虑到Cu2-xSe以430 K为界,存在低温的α相和高温的β相两种不同的相态结构[13-14],因此选择β-Cu2-xSe存在的温度区间500~1000 K进行研究,设定时间步长为1 ps。模拟中首先对系统进行能量最小化以消除系统内不合理的应力,然后在NPT(恒压、恒温)系综下运行50 ps,使系统达到平衡状态,并在之后的60 ns内以5 ns为周期输出材料的导热系数和扩散系数。本工作使用的控温方法为Nose-Hoover法[15]。模拟中均采用周期性边界条件,使用分子模拟软件LAMMPS[16]进行计算。
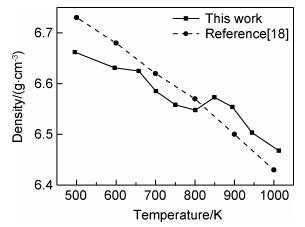
1.2 模型验证为了验证莫尔斯势参数和所建立模型的正确性,计算β-Cu2Se在压强为0.1 MPa,温度区间为500~1000 K的密度,结果示于图 2。由图 2可知,β-Cu2Se在500 K时的密度为6.67 g/cm3,与文献[17]中实验所得高温相Cu2Se密度(6.703 g/cm3)相一致。将计算所得500~1000 K的密度与文献[18]实验所得结果进行对比验证,相对误差在2%之内,因此模拟结果具有可靠性和准确性。此外,曲线在850 K左右出现转折,密度增加到6.573 g/cm3,这和文献[10]发现β-Cu2-xSe在800 K左右存在的玻璃化转变相符。
|
图 2 β-Cu2Se在不同温度下的密度 Fig. 2 Density of β-Cu2Se at different temperatures |
扩散系数通过计算系统的均方位移而得到,均方位移由式(2)所定义:
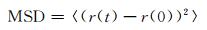
|
(2) |
式中:MSD为粒子的均方位移;r(t)为时间t时粒子的位置;r(0)为开始时刻粒子的位置。
依据爱因斯坦扩散定律[19],在长时间跨度下均方位移对时间曲线斜率的1/6即为系统整体的扩散系数:
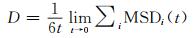
|
(3) |
式中:D为系统中粒子的扩散系数;t为模拟时长;MSD为粒子的均方位移。
导热系数的计算采用平衡分子动力学(equilibrium molecule dynamics,EMD)模拟方法,也称为Green-Kubo法[20-21],该算法的基本思想是通过计算热流量自相关函数(heat flux auto correlation function,HFACF)得到材料的导热系数k,即:
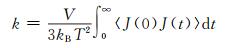
|
(4) |
式中:kB为玻尔兹曼常数;T为热力学温度;V为系统体积;t为模拟时长;尖括号意指对时间的平均;J(0)和J(t)表示在0时刻和t时刻的热流量,并且可以由式(5)得到:
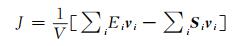
|
(5) |
式中:J为热流量;V为体积;Ei表示第i个粒子所具有的能量,包含势能和动能;vi为速度矢量;Si表示作用在第i个粒子上的应力张量。
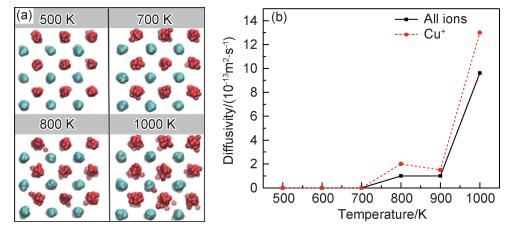
2 结果与讨论 2.1 扩散特性及导热系数相关性“声子液体”热电材料的结构特殊性在于其中存在的类“液态”离子。本工作分析在500,700,800 K和1000 K时系统内离子的运动轨迹范围,结果示于图 3(a)。由图 3(a)可知,随着温度的升高,离子的运动范围扩大。值得注意的是,相比Se2-,Cu+的移动范围更大,运动更剧烈。此外,离子“液态”性可由扩散系数来具体衡量。对于所有离子、Cu+和Se2-分别应用爱因斯坦扩散定律,计算得到β-Cu2-xSe在500~1000 K间的动态扩散系数,500~1000 K下Se2-均未出现扩散现象,整个系统和Cu+的扩散系数示于图 3(b),由图 3(b)可以看出,随着温度的升高,系统在700 K时出现扩散现象,并在800 K时出现了扩散系数的下降,这和通过密度分析发现的800 K左右玻璃化转变一致。此外,Cu+的扩散系数在趋势与数值上都和整体扩散系数一致。由此可见,β-Cu2-xSe的扩散系数主要由其中的类“液态”的Cu+所贡献,而Se2-构成了十分稳定的亚晶格结构。
|
图 3 β-Cu2Se中的离子扩散 (a)在NPT系综下运行10 ps时离子运动轨迹示意图;(b)所有离子和Cu+的扩散系数随温度的变化曲线 Fig. 3 Diffusion of ions in β-Cu2Se (a)trajectories of ions under the NPT ensemble for 10 ps; (b)diffusivities of all ions and Cu+ in β-Cu2Se at different temperatures |
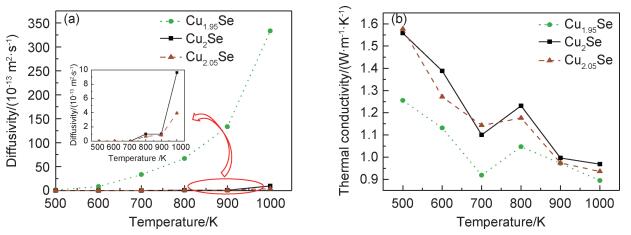
为研究类“液态”离子的扩散和β-Cu2-xSe导热系数的相关性,计算不同温度(500~1000 K)和不同配位数(1.95,2.00和2.05)下的导热系数和扩散系数,所得结果示于图 4。图 4(a)表明对于β-Cu2-xSe,温度的升高和配位数的下降都会导致材料扩散系数的增加。在温度为800 K左右时出现的导热系数“逆”增长也符合β-Cu2-xSe在800 K左右存在的玻璃化转变现象(图 4(b))。排除玻璃态转化的影响,β-Cu2-xSe的导热系数整体随温度升高而下降。这意味着温度的升高加剧了离子的运动,导致晶格非简谐振动的增加,传热过程中晶格非简谐振动的加剧则使得声子散射更加强烈,在宏观层面上体现为导热系数的下降。
|
图 4 β-Cu1.95Se,β-Cu2Se和β-Cu2.05Se在不同温度下的扩散系数(a)和导热系数(b) Fig. 4 Diffusivity(a) and thermal conductivity(b) of β-Cu1.95Se, β-Cu2Se and β-Cu2.05Se at different temperatures |
综合比较β-Cu2-xSe的扩散系数和导热系数,β-Cu2-xSe扩散系数的增加和导热系数的降低具有同步性。Cu+的扩散能力提高引起晶格非简谐振动的增加,从而导致材料导热系数的降低。以上结果表明类“液态”离子的扩散能力和材料导热系数具有很强的相关性。
2.2 掺杂和空位为了分析掺杂和空位对β-Cu2-xSe的导热性能的影响,计算3种不同配位数β-Cu1.95Se,β-Cu2Se和β-Cu2.05Se的导热系数,结果示于图 4(b)。由图 4(b)可知,β-Cu2Se和β-Cu2.05Se导热系数的变化趋势和范围大致相同,均从1.56 W/(m·K)下降至0.97 W/(m·K)左右,但当温度处于500~800 K,β-Cu1.95Se的导热系数相比前两者都更低。上述结果表明,当材料形成空位时,Cu+获得更多的移动空间,使得晶格存在更多的非简谐振动,从而降低了导热系数;与此相反,掺杂对导热系数的影响不明显,当晶体内未留有明显的移动空间给Cu+时,增加Cu+的数量不能明显增加晶格整体的非简谐振动,对导热系数的影响并不显著。由此可见,晶体结构的完备性对导热系数造成的影响主要体现在晶体内部是否提供足够空间给类“液态”离子进行移动迁移。
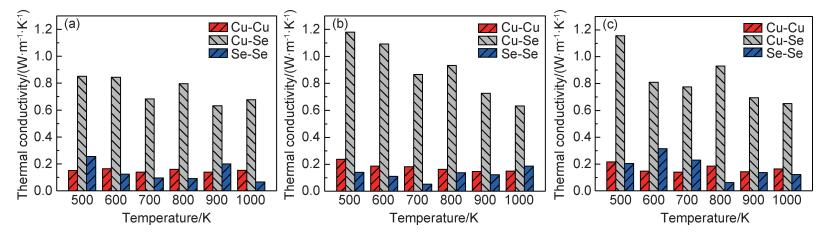
2.2.1 不同离子作用为了进一步分析掺杂和空位对热传导过程的影响,将导热系数分解为不同离子作用贡献项以研究掺杂和空位处理后不同离子间相互作用对导热系数的影响。依据公式(6)将导热系数分为铜-铜相互作用项(Cu-Cu项)、铜-硒相互作用项(Cu-Se项)和硒-硒相互作用项(Se-Se项)[22],所得结果示于图 5。
|
图 5 不同离子热导率贡献项在不同温度下的分布 (a)β-Cu1.95Se;(b)β-Cu2Se;(c) β-Cu2.05Se Fig. 5 Contribution of different ion pairs to the total conductivity at different temperatures (a)β-Cu1.95Se; (b)β-Cu2Se; (c)β-Cu2.05Se |
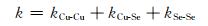
|
(6) |
式中:k为导热系数,不同下标表示对应离子间相互作用对导热系数的贡献项。
从图 5可以看出,在β-Cu2-xSe导热系数的构成中,Cu-Se项构成了最大组成部分,贡献了约占72%的能量传递,成为最主要的热量传递方式。掺杂和空位处理后导热系数的区别也主要体现在Cu-Se项的异同。相比β-Cu2Se和β-Cu2.05Se,存在空位的β-Cu1.95Se中Cu-Se项更低并且随温度的变化不明显,说明当材料内部存在足够移动空间时,类“液态”离子倾向于在内部空位间的移动,与固定框架的碰撞概率降低。此外,温度的提高对类“液态”离子移动的选位影响不大。由此可知,材料内部存在的空位使得类“液态”离子的移动集中于空间缺陷点,降低了和晶格框架的碰撞概率,有效地降低了导热系数。相比空位,掺杂的影响则不明显。
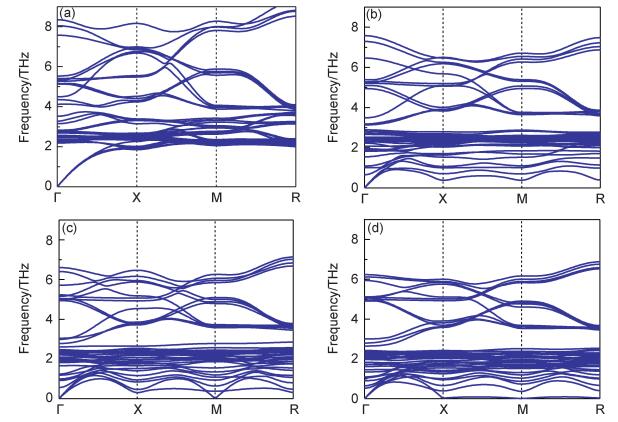
2.2.2 声子输运特征晶格振动理论[23]认为,晶体中的热传导主要依靠声子输运来完成。晶体内部存在温度梯度时,材料内部声子的移动把能量从高温端传递到低温端。为进一步分析空位对导热系数的影响机制,本工作应用Kong等[24-26]提出的方法分别计算700 K下配位数2.000,1.969,1.938和1.906的声子色散曲线,结果示于图 6。由图 6可知,随着材料内部空位的增加,热传导相关的声学支声子频率下降,声学支声子的散射增强。材料内部的空位影响了声学支声子的输运,影响了晶体内部能量的传递,从而降低了材料的导热系数。
|
图 6 β-Cu2-xSe在700 K的色散关系 (a)β-Cu2Se;(b)β-Cu1.969Se;(c)β-Cu1.938Se;(d)β-Cu1.906Se Fig. 6 Dispersion relations of β-Cu2-xSe at 700 K (a)β-Cu2Se; (b)β-Cu1.969Se; (c)β-Cu1.938Se; (d)β-Cu1.906Se |
(1)“声子液体”热电材料中类“液态”离子扩散能力的增大和材料导热系数的降低具有极强的相关性。类“液态”离子移动能力的提高会导致晶格的非简谐振动增加,从而降低材料的导热系数。
(2) 材料内部形成的空位有利于离子的移动,从而降低导热系数;材料掺杂对导热系数的影响不明显。空位的存在使得Cu+在移动过程中倾向于在内部空间的移动,其具体影响在于空位使得声子声学支频率降低,影响了晶体内部能量的传递,降低材料的导热系数。
| [1] |
BELL L E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems[J]. Science, 2008, 321(5895): 1457-1461. DOI:10.1126/science.1158899 |
| [2] |
SNYDER G J, TOBERER E S. Complex thermoelectric materials[J]. Nature Materials, 2008, 7(2): 105-114. DOI:10.1038/nmat2090 |
| [3] |
YANG J, XI L, QIU W, et al. On the tuning of electrical and thermal transport in thermoelectrics: an integrated theory-experiment perspective[J]. Npj Computational Materials, 2016(2): 15015. |
| [4] |
ZEBARJADI M, ESFARJANI K, DRESSELHAUS M S, et al. Perspectives on thermoelectrics: from fundamentals to device applications[J]. Energy & Environmental Science, 2012, 5(1): 5147-5162. |
| [5] |
GOLDSMID H J. Introduction to thermoelectricity[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2010.
|
| [6] |
刘灰礼, 何颖, 史迅, 等. "声子液体"热电材料研究进展[J]. 科学通报, 2013, 57(25): 2603-2608. LIU H L, HE Y, SHI X, et al. Recent progress in "phonon-liquid" thermoelectric materials(in Chinese)[J]. China Sci Bull(Chin Ver), 2013, 57(25): 2603-2608. |
| [7] |
LIU H, SHI X, XU F, et al. Copper ion liquid-like thermoelectrics[J]. Nature Materials, 2012, 11(5): 422-425. DOI:10.1038/nmat3273 |
| [8] |
OUYANG T, ZHANG X, HU M. Thermal conductivity of ordered-disordered material: a case study of superionic Ag2Te[J]. Nanotechnology, 2014, 26(2): 025702. |
| [9] |
LIANG X. Mobile copper ions as heat carriers in polymorphous copper sulfide superionic conductors[J]. Applied Physics Letters, 2017, 111(13): 133902. DOI:10.1063/1.4997501 |
| [10] |
KIM H, BALLIKAYA S, CHI H, et al. Ultralow thermal conductivity of β-Cu2Se by atomic fluidity and structure distortion[J]. Acta Materialia, 2015, 86: 247-253. DOI:10.1016/j.actamat.2014.12.008 |
| [11] |
MORSE P M. Diatomic molecules according to the wave mechanics[J]. Physical Review, 1929, 34(1): 57-64. DOI:10.1103/PhysRev.34.57 |
| [12] |
NAMSANI S, GAHTORI B, AULUCK S, et al. An interaction potential to study the thermal structure evolution of a thermoelectric material: β-Cu2Se[J]. Journal of Computational Chemistry, 2017, 38(25): 2161-2170. DOI:10.1002/jcc.24865 |
| [13] |
MACHADO K D, DE LIMA J C, GRANDI T A, et al. Structural study of Cu2-xSe alloys produced by mechanical alloying[J]. Acta Crystallographica Section: B, 2004, 60(3): 282-286. DOI:10.1107/S0108768104007475 |
| [14] |
何新民, 张婷, 陈飞, 等. Cu2Se基"声子液体"类热电材料[J]. 化学进展, 2017, 29(11): 1357-1365. HE X M, ZHANG T, CHEN F, et al. Cu2Se-based phonon liquid thermoelectric materials[J]. Progress in Chemistry, 2017, 29(11): 1357-1365. |
| [15] |
MARTYNA G J, KLEIN M L, TUCKERMAN M. Nosé-Hoover chains: the canonical ensemble via continuous dynamics[J]. The Journal of Chemical Physics, 1992, 97(4): 2635-2643. DOI:10.1063/1.463940 |
| [16] |
PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19. DOI:10.1006/jcph.1995.1039 |
| [17] |
GULAY L, DASZKIEWICZ M, STROK O, et al. Crystal structure of Cu2Se[J]. Chemistry of Metals and Alloys, 2011(4): 200-205. |
| [18] |
GAHTORI B, BATHULA S, TYAGI K, et al. Giant enhancement in thermoelectric performance of copper selenide by incorporation of different nanoscale dimensional defect features[J]. Nano Energy, 2015, 13: 36-46. DOI:10.1016/j.nanoen.2015.02.008 |
| [19] |
陈正隆, 徐为人, 汤立达. 分子模拟的理论与实践[M]. 北京: 化学工业出版社, 2007. CHEN Z L, XU W R, TANG L D. Theory and practice of molecular simulation[M]. Beijing: Chemical Industry Press, 2007. |
| [20] |
GREEN M S. Markoff random processes and the statistical mechanics of time-dependent phenomena[J]. Journal of Chemical Physics, 1952, 20(8): 1281-1295. DOI:10.1063/1.1700722 |
| [21] |
KUBO R. Statistical physics Ⅱ: nonequilibrium statistical mechanics[M]. Berlin: Springer-Verlag, 2012.
|
| [22] |
LIN S, BUEHLER M J. Thermal transport in monolayer graphene oxide: atomistic insights into phonon engineering through surface chemistry[J]. Carbon, 2014, 77: 351-359. DOI:10.1016/j.carbon.2014.05.038 |
| [23] |
KITTEL C. Introduction to solid state physics[M]. New York: Wiley, 1976.
|
| [24] |
KONG L T, DENNISTON C, MVSER M H. Improved version of the Green's function molecular dynamics method[J]. Computer Physics Communications, 2011, 182(2): 540-541. DOI:10.1016/j.cpc.2010.10.006 |
| [25] |
KONG L T, BARTELS G, CAMPAÑÁ C, et al. Implementation of Green's function molecular dynamics: an extension to LAMMPS[J]. Computer Physics Communications, 2009, 180(6): 1004-1010. DOI:10.1016/j.cpc.2008.12.035 |
| [26] |
KONG L T. Phonon dispersion measured directly from molecular dynamics simulations[J]. Computer Physics Communications, 2011, 182(10): 2201-2207. DOI:10.1016/j.cpc.2011.04.019 |
 2021, Vol. 49
2021, Vol. 49


