文章信息
- 周亚利, 杨秋月, 张文玮, 刘田文, 何威, 吴珍, 伍铭, 谭元标
- ZHOU Ya-li, YANG Qiu-yue, ZHANG Wen-wei, LIU Tian-wen, HE Wei, WU Zhen, WU Ming, TAN Yuan-biao
- 具有层片状α相组织的TB8钛合金热变形行为及本构方程
- Hot deformation behavior and constitutive equation of TB8 titanium alloy with a lamellar structure of α phase
- 材料工程, 2021, 49(1): 75-81
- Journal of Materials Engineering, 2021, 49(1): 75-81.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000307
-
文章历史
- 收稿日期: 2020-04-11
- 修订日期: 2020-10-12
2. 贵州大学 贵州省材料结构与强度重点实验室, 贵阳 550025
 三者之间的关系已通过Arrhenius-type本构方程进行表征,建立了材料常数α,A,n和Q值与真应变之间的关系模型,并分析了应变对α,A,n和Q值的影响。α值随真应变的增加而增加,而A,n和Q的值随真应变的增加而逐渐降低。实验应力值和预测应力值之间的相关系数和平均相对误差参数分别为0.945和9.08%。这表明本工作建立的应变补偿的热变形本构方程能够很好地预测具有层片状α相组织的TB8钛合金在α+β双相区热变形过程中的流变应力。
三者之间的关系已通过Arrhenius-type本构方程进行表征,建立了材料常数α,A,n和Q值与真应变之间的关系模型,并分析了应变对α,A,n和Q值的影响。α值随真应变的增加而增加,而A,n和Q的值随真应变的增加而逐渐降低。实验应力值和预测应力值之间的相关系数和平均相对误差参数分别为0.945和9.08%。这表明本工作建立的应变补偿的热变形本构方程能够很好地预测具有层片状α相组织的TB8钛合金在α+β双相区热变形过程中的流变应力。2. Guizhou Key Laboratory of Materials Mechanical Behaviour and Microstructure, Guizhou University, Guiyang 550025, China
 and is characterized by Arrhenius-type constitutive equation. The equation between the material constants (α, Q, n and lnA) and strain is constructed. The effect of strain on the material constants (α, Q, n and lnA) of the Arrhenius-type constitutive equation is analyzed. The value of α is increased with true strain, while the values of Q, n and lnA are gradually decreased. The correlation coefficient (R2) and the AARE value between the experimental and the predicted stress are 0.945 and 9.08%, respectively. This indicates that the strain-compensates Arrhenius type constitutive equation can better predict the flow stress value under different deformation conditions for the TB8 titanium alloy with a lamellar α structure deformed in the α+β dulex phase region.
and is characterized by Arrhenius-type constitutive equation. The equation between the material constants (α, Q, n and lnA) and strain is constructed. The effect of strain on the material constants (α, Q, n and lnA) of the Arrhenius-type constitutive equation is analyzed. The value of α is increased with true strain, while the values of Q, n and lnA are gradually decreased. The correlation coefficient (R2) and the AARE value between the experimental and the predicted stress are 0.945 and 9.08%, respectively. This indicates that the strain-compensates Arrhenius type constitutive equation can better predict the flow stress value under different deformation conditions for the TB8 titanium alloy with a lamellar α structure deformed in the α+β dulex phase region.钛合金因优异的室温和高温力学性能、良好的焊接性能和耐腐蚀性能被广泛用作航空领域的钣金零件、大型锻件、焊接件以及紧固件[1-2]。钛合金构件的力学性能取决于热成形加工后所形成的微观组织。采用合适的热成形加工工艺可获得力学性能优异的微观组织[3]。目前,对于钛合金的热锻成形加工方法,主要在α+β双相区加工、近β相区加工和单β相区加工[4-6]。但是,在不同温度区间进行热加工,合金构件的组织会有所区别,这会导致其力学性能也呈现出较大差异。
TB8钛合金是一种亚稳态β型钛合金,因超高的强度以及高的合金含量,导致其热加工范围较窄。为了控制合金构件的微观组织和改善合金的力学性能,需要深入研究该合金的热变形行为。近年来,关于TB8钛合金热变形行为的研究仅有少量文献报道[7-9]。Duan等[7]和Tang等[8]研究了锻态具有少量α相组织的TB8钛合金的热变形行为,构建了该合金的热变形本构方程。前期工作中,本课题组已研究了具有不同初始β晶粒尺寸的TB8钛合金单β相区的热变形行为,分析了不同晶粒尺寸和热加工参数对该合金热加工行为的作用机理,构建了热变形本构模型。基于热加工图分析,获得了具有不同晶粒尺寸的TB8钛合金的最优热加工参数[9]。TB8钛合金的热变形行为是显著依赖于合金的初始组织和热加工参数。根据文献报道[10-12],对于具有层片状α相组织的钛合金在α+β双相区进行热加工,可获得球状α相和β相的双相组织。这种组织表现出高的塑性和室温强度以及优异的疲劳性能[2]。然而,具有层片状α相组织的TB8钛合金在α+β双相区的热变形行为鲜见报道。
为了改善TB8钛合金的疲劳性能,本工作将深入研究具有层片状α相组织的TB8钛合金在α+β双相区的热变形行为,分析具有层片状α相组织的TB8钛合金的流变行为,建立热加工参数与流变应力之间的本构模型,并预测不同变形条件下的流变应力。
1 实验材料与方法本工作采用TB8钛合金为锻造棒材,Tβ转变温度为815 ℃[9],该合金的成分如表 1所示。将初始态合金进行1200 ℃,保温1 h的退火热处理,随后炉冷至室温。合金经热处理后的初始组织如图 1所示,粗大的β相晶粒内部包含大量层片状α相。将经热处理的样品加工成ϕ8 mm×12 mm的热变形试样。为了研究具有初始层片状α相组织的TB8钛合金的热变形行为及本构模型,采用Gleeble 3500热模拟压缩机对合金进行热变形实验。变形温度为650~800 ℃,温度间隔为50 ℃,应变速率为0.001~1 s-1,真应变为0.7。将试样以10 ℃/s的速率直接加热到实验设定的变形温度,保温5 min以消除试样内外的温度梯度。变形后立即水冷到室温。
| Mo | Al | Nb | Si | Fe | C | N | O | H | Ti |
| 14.5 | 2.9 | 2.85 | 0.19 | 0.07 | 0.02 | 0.02 | 0.09 | 0.002 | Bal |

|
图 1 TB8钛合金在1200 ℃,保温1 h退火处理后的金相组织 Fig. 1 Microstructure of the TB8 titanium alloy after annealing treatment at 1200 ℃ for 1 h |
图 2为TB8钛合金在不同变形条件下的真应力-应变曲线,在变形条件为650 ℃/1 s-1时,如图 2(a)所示,流变应力随真应变增加快速增加,并达到一个峰值,随后随真应变的增加缓慢降低,呈现一个连续屈服现象。类似的现象也曾在具有初始层片状α相组织的47Zr-45Ti-5Al-3V合金中观察到[12]。这种连续的屈服现象主要与流变局部带的形成、变形热、层状α相的球化等微观组织变化有关。随着变形温度从700 ℃升高到800 ℃,变形初期阶段的流变曲线可观察到一个显著的不连续屈服现象。对于钛合金,这种不连续屈服现象主要发生在β相区的热变形过程中或者是具有单β相组织的钛合金在β相区的热变形过程中。在钛合金中,这种不连续屈服现象目前有两种理论可以解释:静态理论[13]和动态理论[14-15]。但Ankem等[16]研究发现Ti-V和Ti-Mn合金在高温拉伸变形后,在同一温度下再次变形时并未再现不连续屈服现象。因此,他们认为静态理论并不能很好地解释这种现象。对于动态理论,该理论认为不连续屈服现象与大量可动位错突然从晶界增殖有关。在本工作中,具有初始层片状α相的TB8钛合金的热成形是在α+β双相区进行,这表明合金在变形过程中发生了α→β相的转变。众所周知,热变形过程中,可动位错密度是依赖于应变速率。两者之间可用如下关系描述[16]:
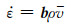
|
(1) |
|
图 2 TB8钛合金在不同变形条件下的真应力-应变曲线
(a) = 1 s-1; (b) = 1 s-1; (b) =0.1 s-1; (c) =0.1 s-1; (c) =0.01 s-1; (d) =0.01 s-1; (d) =0.001 s-1
Fig. 2 True stress-strain curves for the TB8 titanium alloy deformed under different conditions
(a) =0.001 s-1
Fig. 2 True stress-strain curves for the TB8 titanium alloy deformed under different conditions
(a) =1 s-1; (b) =1 s-1; (b) =0.1 s-1; (c) =0.1 s-1; (c) =0.01 s-1; (d) =0.01 s-1; (d) =0.001 s-1 =0.001 s-1
|
式中:
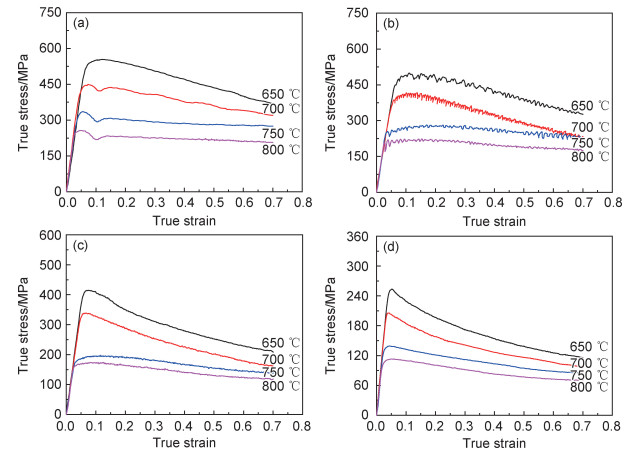
热变形过程中,应变速率(


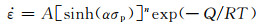
|
(2) |
|
图 3 TB8钛合金峰值应力与应变速率的关系 Fig. 3 Relationship between the peak-stress and strain rate for the TB8 titanium alloy |
|
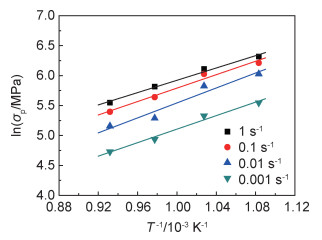
图 4 TB8钛合金峰值应力与变形温度的关系 Fig. 4 Relationship between the peak-stress and deformation temperature for the TB8 titanium alloy |
式中:Q为形变激活能;R为理想气体常数;A,α,n为与温度无关的材料常数。将式(2)取对数,得出以下公式:
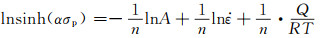
|
(3) |
将实验数据代入式(3),计算分析可得:α=0.00344 MPa-1;Q=415.096 kJ/mol;n=6.57;A=7.46×1019 s-1。
因此,σp, T和
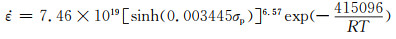
|
(4) |
在金属热加工过程中,T和

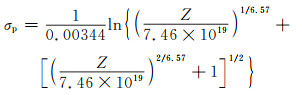
|
(5) |
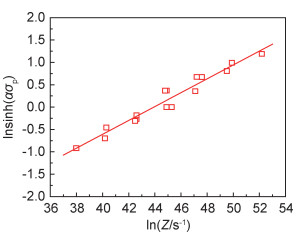
|
图 5 TB8钛合金峰值应力(σp)与Z参数之间的关系 Fig. 5 Relationship between the peak-stress (σp) and the Z parameter for the TB8 titanium alloy |
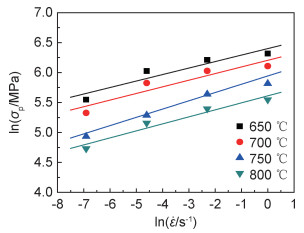
通过式(3)计算出Q=415.096 kJ/mol, 代入Zener-Hollomon(Z=
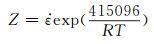
|
(6) |
通常,根据公式(3)计算合金热变形激活能以及材料常数时忽略了应变对流变行为的作用。然而,一些文献已报道,热变形过程中的热变形激活能和材料常数会受到应变的影响[19-20]。为了分析热变形激活能和材料常数与应变之间的定量关系,可认为Q,α,n和lnA是与应变相关的多项式函数,在本构方程中考虑应变的影响。α,A,n和Q与真应变ε之间可分别用式(7)~(10)的五次多项式表示。
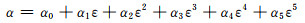
|
(7) |
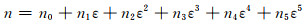
|
(8) |
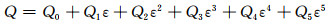
|
(9) |
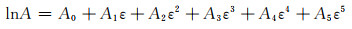
|
(10) |
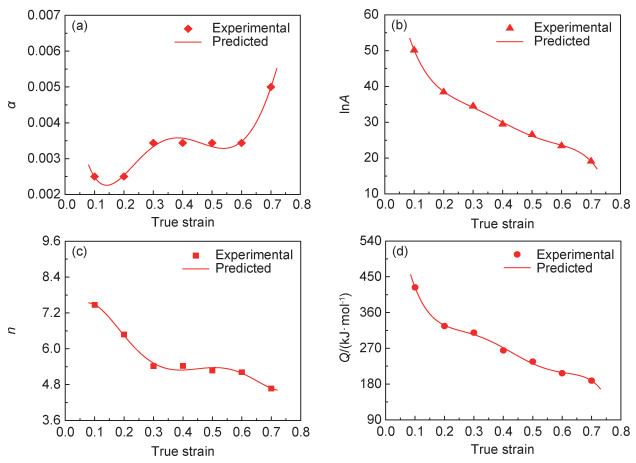
先根据式(2),(3)计算出不同应变条件下的α,A,n和Q值。然后将其带入式(7)~(10)求出方程的各项系数,即可获得α,A,n和Q值与ε之间多项式关系表达式。式(7)~(10)的各项系数如表 2所示。不同应变条件下α,lnA,n和Q值的变化情况如图 6所示,表明根据实验数据和多项式函数计算获得的形变激活能和材料常数保持良好的相关性。从图 6中可以观察到,α值是随真应变的增加而增加,而A,n和Q值是随真应变的增加而逐渐降低。
| α | n | Q/(kJ·mol-1) | ln(A/s-1) |
| α0=0.00653 | n0=6.36 | Q0=816.93 | A0=87.37 |
| α1=-0.07831 | n1=35.27 | Q1=-6683.08 | A1=-604.09 |
| α2=0.4905 | n2=-330.13 | Q2=-35624.08 | A2=2994.58 |
| α3=-1.24693 | n3=-1019.87 | Q3=-92680.42 | A3=-7689.02 |
| α4=1.3697 | n4=-1327.65 | Q4=-112958.33 | A4=9511.36 |
| α5=-0.525 | n5=620.83 | Q5=51991.67 | A5=-4516.67 |
|
图 6 不同应变条件下α, lnA, n和Q值的变化情况 (a)α; (b)lnA; (c)n; (d)Q Fig. 6 Value of the α, lnA, n and Q under different true strains (a)α; (b)lnA; (c)n; (d)Q |
当修正的α,A,n和Q值计算出之后,可根据如下方程预测不同应变条件下的流变应力值:
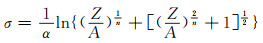
|
(11) |
图 7为TB8钛合金在不同应变速率下实验流变应力与预测流变应力的比较。如图 7所示,在所有变形条件下实验获得的流变应力值与式(11)预测的流变应力值之间都保持较高的吻合度。为了进一步分析实验获得的流变应力与本构方程预测的流变应力之间的相关性,可利用两者之间的相关系数(R2)和平均相对误差(AARE)参数来进行定量分析。两者之间的R2和AARE值可通过式(12),(13)进行计算[20-21]:
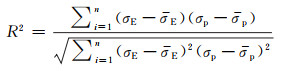
|
(12) |
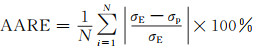
|
(13) |
|
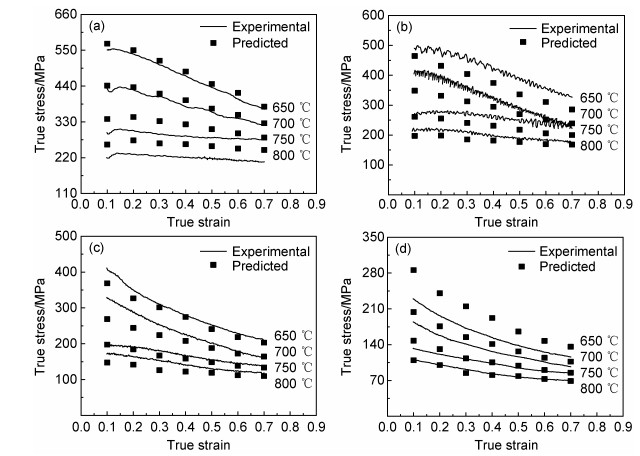
图 7 TB8钛合金在不同应变速率下实验流变应力与预测流变应力的比较
(a) = 1 s-1; (b) = 1 s-1; (b) =0.1 s-1; (c) =0.1 s-1; (c) =0.01 s-1; (d) =0.01 s-1; (d) =0.001 s-1
Fig. 7 Comparison of the experimental and predicted flow stress for the TB8 titanium alloy deformed under different conditions
(a) =0.001 s-1
Fig. 7 Comparison of the experimental and predicted flow stress for the TB8 titanium alloy deformed under different conditions
(a) = 1 s-1; (b) = 1 s-1; (b) =0.1 s-1; (c) =0.1 s-1; (c) =0.01 s-1; (d) =0.01 s-1; (d) =0.001 s-1 =0.001 s-1
|
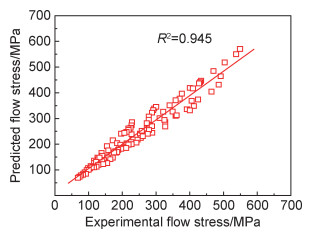
式中:σE和σp分别为实验应力和预测应力;σE和σp分别为对应的应力平均值;N为本工作测试的实验条件总数。图 8为不同变形条件下预测应力与实验应力的相关性,由图可知,实验应力和本构方程预测的流变应力之间具有良好的相关性。在本工作中,R和AARE值经计算分别为0.945和9.08%,这表明了上述建立的本构方程能够很好地表征σp,T和
|
图 8 不同变形条件下预测应力与实验应力的相关性 Fig. 8 Correlation between the predicted and experimental flow stress under different deformation conditions |
(1) 在应变速率为1 s-1时,650 ℃变形的流变曲线展现出连续的流变软化,当温度高于650 ℃时,流变曲线展现出一个应力降现象。随应变速率的降低和温度的增加,应力降现象消失。当应变速率为0.001 s-1时,750 ℃和800 ℃的流变曲线呈现出动态再结晶特征。
(2) σp,T和
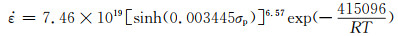
|
(3) α,A,n和Q值与真应变ε之间的关系模型已建立。应变对α,A,n和Q值的影响已分析。α值是随真应变的增加而增加,而A,n和Q值是随应变的增加而逐渐降低。实验应力值和预测应力值之间的相关系数和平均相对误差参数分别为0.945和9.08%。
| [1] |
LIN Y C, TANG Y, ZHANG X Y, et al. Effects of solution temperature and cooling rate on microstructure and micro-hardness of a hot compressed Ti-6Al-4V alloy[J]. Vacuum, 2019, 159: 191-199. DOI:10.1016/j.vacuum.2018.10.035 |
| [2] |
AI Y, ZHU S P, LIAO D, et al. Probabilistic modelling of notch fatigue and size effect of components using highly stressed volume approach[J]. International Journal of Fatigue, 2019, 127: 110-119. DOI:10.1016/j.ijfatigue.2019.06.002 |
| [3] |
WU Y, KOU H C, WU Z H, et al. Dynamic recrystallization and texture evolution of Ti-22Al-25Nb alloy during plane-strain compression[J]. Journal of Alloys and Compounds, 2018, 749: 844-852. DOI:10.1016/j.jallcom.2018.03.372 |
| [4] |
GHASEMI E, ZAREI-HANZAKI A, FARABI E, et al. Flow softening and dynamic recrystallization behavior of BT9 titanium alloy:a study using process map development[J]. Journal of Alloys and Compounds, 2017, 695: 1706-1718. DOI:10.1016/j.jallcom.2016.10.322 |
| [5] |
GAO Y, MA G Q, ZHANG X Y, et al. Microstructure evolution and hot deformation behavior of Ti-6.5Al-2Zr-1Mo-1V alloy with starting lamellar structure[J]. Journal of Alloys and Compounds, 2019, 809: 151852. DOI:10.1016/j.jallcom.2019.151852 |
| [6] |
LIN Y C, PANG G D, JIANG Y Q, et al. Hot compressive deformation behavior and microstructure evolution of a Ti-55511 alloy with basket-weave microstructures[J]. Vacuum, 2019, 169: 108878. DOI:10.1016/j.vacuum.2019.108878 |
| [7] |
DUAN Y P, LI P, XUE K M, et al. Flow behavior and microstructure evolution of TB8 alloy during hot deformation process[J]. Transactions of Nonferrous Metals Society of China, 2007, 17: 1199-1204. DOI:10.1016/S1003-6326(07)60249-0 |
| [8] |
TANG B, TANG B, HAN F B, et al. Hot deformation behavior of TB8 alloy near the β-Transus[J]. Rare Metal Materials and Engineering, 2013, 42(9): 1761-1766. DOI:10.1016/S1875-5372(14)60001-1 |
| [9] |
YANG Q Y, MA M, TAN Y B, et al. Initial β grain size effect on high-temperature flow behavior of TB8 titanium alloys in single β phase field[J]. Metals, 2019, 9(8): 890-909. DOI:10.3390/met9080890 |
| [10] |
ZHAO Y L, LI B L, ZHU Z S, et al. The high temperature deformation behavior and microstructure of TC21 titanium alloy[J]. Materials Science and Engineering:A, 2010, 527: 5360-5367. DOI:10.1016/j.msea.2010.05.076 |
| [11] |
MA X, ZENG W D, SUN Y, et al. Modeling constitutive relationship of Ti17 titanium alloy with lamellar starting microstructure[J]. Materials Science and Engineering:A, 2012, 538: 182-189. DOI:10.1016/j.msea.2012.01.027 |
| [12] |
TAN Y B, JI L Y, DUAN J L, et al. A study on the hot deformation behavior of 47Zr-45Ti-5Al-3V alloy with initial lamellar α structure[J]. Metallurgical and Materials Transactions A, 2016, 47(12): 5974-5984. DOI:10.1007/s11661-016-3703-4 |
| [13] |
赖运金, 曾卫东, 张驰, 等. Ti-17合金高温变形中的不连续屈服与流变软化研究[J]. 机械科学与技术, 2007(9): 1183-1186. LAI Y J, ZENG W D, ZHANG C, et al. Study on discontinuous yield and rheological softening of Ti-17 alloy during high temperature deformation[J]. Mechanical Science and Technology, 2007(9): 1183-1186. DOI:10.3321/j.issn:1003-8728.2007.09.022 |
| [14] |
PHILIPPART I, RACK H J. High temperature dynamic yielding in metastable Ti-6.8Mo-4.5F-1.5A[J]. Materials Science and Engineering:A, 1998, 243: 196-200. DOI:10.1016/S0921-5093(97)00800-9 |
| [15] |
ZHOU W, GE P, ZHAO Y Q, et al. Discontinuous yielding in high temperature deformation of Ti-5553 alloy[J]. Rare Metal Materials and Engineering, 2015, 44(10): 2415-2418. DOI:10.1016/S1875-5372(16)30032-7 |
| [16] |
ANKEM S, SHYUE J G, VIJAYSHANKAR M N, et al. The effect of volume percent of phase on the high temperature tensile deformation of two-phase Ti-Mn alloys[J]. Materials Science and Engineering:A, 1989, 111: 51-61. DOI:10.1016/0921-5093(89)90197-4 |
| [17] |
TAN Y B, JI L Y, LIU W C, et al. Effect of hot deformation on α→β phase transformation in 47Zr-45Ti-5Al-3V alloy[J]. Transactions of Nonferrous Metals Society of China, 2018, 28: 1947-1957. DOI:10.1016/S1003-6326(18)64840-X |
| [18] |
钱匡武, 彭开萍, 陈文哲. 金属动态应变时效现象中的"锯齿屈服"[J]. 福建工程学院学报, 2003, 1(1): 4-8. QIAN K W, PENG K P, CHEN W Z. Features of serrated yielding of dynamic strain aging phenomenon in metals and alloys[J]. Journal of Fujian University of Technology, 2003, 1(1): 4-8. DOI:10.3969/j.issn.1672-4348.2003.01.002 |
| [19] |
RADOVIC N, DROBNJAK D. Effect of interpass time and cooling rate on apparent activation energy for hot working and critical recrystallization temperature of Nb-microalloyed steel[J]. ISIJ International, 1999, 39(6): 575-582. DOI:10.2355/isijinternational.39.575 |
| [20] |
ABBASI-BANI A, ZAREI-HANZAKI A, PISHBIN M H, et al. A comparative study on the capability of Johnson-Cook and Arrhenius-type constitutive equations to describe the flow behaviour of Mg-6Al-1Zn alloy[J]. Mechanics of Materials, 2014, 71: 52-61. DOI:10.1016/j.mechmat.2013.12.001 |
| [21] |
MANDAL S, RAKESH V, SIVAPRASAD P V, et al. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel[J]. Materials Science and Engineering:A, 2009, 500(1/2): 114-121. |
 2021, Vol. 49
2021, Vol. 49


