文章信息
- 张景祺, 林健, 雷永平, 许海亮, 王细波
- ZHANG Jing-qi, LIN Jian, LEI Yong-ping, XU Hai-liang, WANG Xi-bo
- 316L超薄板激光焊接的失稳变形规律
- Instability deformation analysis of laser welded joint of 316L ultra-thin plate
- 材料工程, 2020, 48(12): 126-134
- Journal of Materials Engineering, 2020, 48(12): 126-134.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.001168
-
文章历史
- 收稿日期: 2019-12-17
- 修订日期: 2020-09-16
2. 北京宇航系统工程研究所, 北京 100076
2. Beijing Institute of Astronautical System Engineering, Beijing 100076, China
超薄板由于其轻薄和易于加工成型的特点,在精密电子、航空航天和核工业等制造领域有着广泛的应用[1-2]。316L不锈钢超薄板具有机械强度高,导电、导热性好,成形性好等优点。但由于其厚度往往仅有0.1 mm,甚至更薄,对热输入极为敏感,容易发生失稳变形。脉冲激光焊具有焊接过程稳定、熔池平静、效率高等特点,在针对316L不锈钢超薄板的连接应用中得到普遍采用[3]。但是由于焊接过程不可避免的局部高密度热量输入与非均匀冷却过程,以及薄板自身刚度较小的原因,其焊接过程与焊后常会发生屈曲。这不仅影响构件的制造精度,而且会因焊后矫直而增加生产成本[4]。使用数值模拟工具分析焊接屈曲的机理,掌握失稳变形规律,可以为相关焊接工艺的选择与优化提供依据。
近年来,国内外学者对焊接屈曲变形问题开展了系列研究并取得了一些成果:Deng等[5]对低碳钢薄板堆焊接头在电弧焊接过程中产生的焊接变形进行了研究。模拟结果表明,随着热输入的增加,屈曲倾向也相应增大。Wang等[6]利用固有应变预测了薄板平面外焊接变形。分析认为纵向固有收缩是引起屈曲的主要原因,而初始挠度和固有弯曲被认为是屈曲的诱因。叶延洪等[7]以3 mm厚铝合金薄板TIG焊单道重熔和MIG对接接头为例,模拟分析焊接残余应力和变形,基于数值模拟结果和实验结果验证了铝合金薄板焊接接头面外变形的形成机理。Huang等[8]基于固有应变理论,采用局部实体模型和整体壳体模型对不同尺寸的激光焊接接头的变形模式和变形幅度进行了较为准确的预测。梁伟等[9]以1 mm厚的薄板为分析对象,通过比较热-弹-塑性有限元法及固有应变法预测的变形结果,分析了焊缝长度对固有变形分布的影响。
针对厚度在1 mm以下的薄板激光焊的研究目前主要有以下工作:Fan等[10]分别使用Nd:YAG激光器、二极管激光器和光纤激光器对0.7 mm厚钛合金薄板进行了焊接实验,实验对比发现Nd:YAG激光焊所得的焊缝质量最佳。Yi等[11]通过模拟与实验对0.1 mm/0.2 mm双层不锈钢薄板的激光叠焊进行了研究,提出了计算焊后薄板整体变形的公式,发现构件的最大形状误差可达3.2 mm。王波等[12]对0.4 mm厚不锈钢板进行了有夹具作用的激光对接焊的实验测量,得到4种不同约束状态下的薄板焊接变形量。结果表明,薄板变形量随着约束强度的增加而减小。然而现有工作中对厚度小于0.1 mm的超薄板焊接过程与焊后的失稳变形的研究还较少。
本研究基于薄板特征值屈曲与后屈曲分析理论,针对0.07 mm厚316L钢箔的激光焊过程建立数值模型,采用有限元软件ABAQUS分析了焊后失稳现象以及相关影响因素,并与实验观测结果进行对比,对数值模型进行验证。
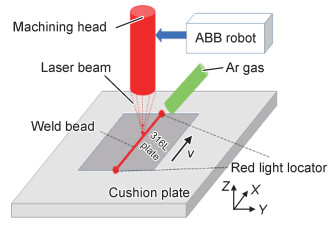
1 实验与测量焊接实验的对象为316L不锈钢箔片,尺寸规格:100 mm(长)×100 mm(宽)×0.07 mm(厚)。焊接前,用丙酮清洗试样表面。采用脉冲激光焊,焊接时通氩气进行保护,气体流量为15 L/min。焊接沿箔片的长度方向(图中的X向)进行。
|
图 1 激光焊接示意图 Fig. 1 Sketch map of laser welding process |
实验中的焊接工艺参数见表 1,焊接过程中激光的焦点在试板的上表面。脉冲激光焊的频率为500 Hz,占空比为20%。对薄板采用Keyence LK-GD500激光位移传感器测量焊后变形,见图 2。
| Welding power/W | Welding speed/(mm·s-1) |
| 100 | 20 |
| 120 | 20 |
| 140 | 20 |
| 140 | 22.5 |

|
图 2 激光位移传感器测量焊后薄板变形 Fig. 2 Deformation measurement of thin plate after welding by laser displacement sensor |
建立10个厚度为0.07 mm的薄板模型, 其几何尺寸(长×宽)分布分别如表 2所示(√表示该平面尺寸(长×宽)的超薄板)。
| Width/mm | Length/mm | ||||
| 36 | 84 | 100 | 160 | 200 | |
| 50 | √ | ||||
| 76 | √ | ||||
| 100 | √ | √ | √ | √ | √ |
| 124 | √ | ||||
| 140 | √ | ||||
| 189 | √ | ||||
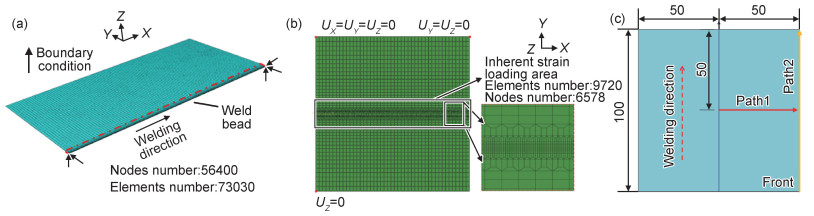
以100 mm×100 mm的模型为例,考虑到结构的对称性,对其1/2大小建立热力耦合模型,其焊缝与邻近区域网格划分较细,远离焊缝区域网格较粗,沿板材厚度方向,共有四层单元。按先后顺序对薄板激光焊接温度场和应力场进行顺序耦合模拟。图 3(a)边界条件的箭头表示模型约束运动的方向(UX, UY, UZ)。
|
图 3 有限元模型与数据选取路径 (a)热力耦合模型;(b)屈曲分析模型;(c)数据选取路径 Fig. 3 Finite element model and data selection path (a)thermo-mechanical coupling model; (b)model of buckling analysis; (c)data selection path |
根据热力耦合的模拟结果确定等效加载区,然后对此区域施加应变载荷进行特征值屈曲分析[13]。屈曲分析有限元模型的网格划分模式与热-弹-塑性模型类似,按比例由焊缝过渡至热影响区。
特征值屈曲分析可以得到薄板在焊后的屈曲变形模态,根据其相应的特征值可以判断薄板是否失稳,失稳时系统的载荷-位移响应出现负刚度,需释放应变能用以维持平衡,要进行后屈曲分析来求解薄板焊后失稳变形量[14]。后屈曲分析模型沿用了特征值屈曲的模型参数,将第一阶正特征值屈曲模态位移向量的1%做为后屈曲分析的初始变形量引入进行计算。
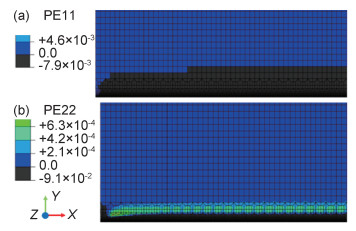
2.2 固有应变载荷的提取提取热力分析计算结果中的残余塑性应变数据,获得固有应变(本研究中主要为塑性应变)的大小与分布,确定等效加载区,将固有应变施加到屈曲分析模型中,进行特征值屈曲分析。图 4为焊接功率P=100 W,焊接速率v=20 mm/s的激光焊后沿焊缝方向压缩塑性应变的分布情况,可以看出此时固有应变区可以认为是包含焊缝及临近区域的一个长方体区域,其截面面积为AW=8 mm(宽度方向)×0.07 mm(厚度方向)。
|
图 4 超薄板激光焊后纵向(a)和横向(b)残余压缩应变场 Fig. 4 Longitudinal (a) and transverse (b) plastic strain distributions of residual plastic strain field of ultra-thin plate after laser welding |
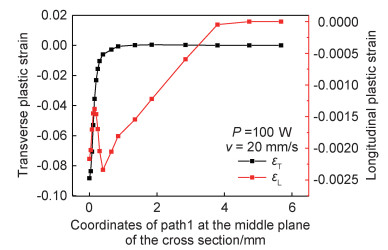
图 5为焊缝中央截面处沿图 3(c) Path1的残余塑性应变的分布情况,可以看出纵向塑性应变值沿此路径呈现绝对值先减小后增大,再减小为0的变化趋势,分布区域较宽;而横向塑性应变的分布区域整体上看明显窄于纵向塑性应变,可以认为纵向固有应变是屈曲变形的主要驱动力来源[15]。
|
图 5 焊缝中点处截面单侧残余塑性应变的分布 Fig. 5 Distributions of unilateral residual plastic strain at midpoint of weld seam |
对于较长焊缝,塑性应变在焊接起始端和末端以外的部位可以近似认为为常数,所以沿着焊接方向选取处于焊缝区域代表性位置(x1,x2……x6)的垂直于焊缝方向的6个截面,对各截面节点上的纵向和横向残余塑性应变值按下式进行积分:
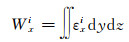
|
(1) |
式中:dy和dz代表模型中相应坐标方向上的距离微分。分别求出各截面处的固有应变εxi与面积的乘积,对各个截面的固有应变与面积乘积的总和(Wx1,Wx2……Wxi)(见表 3)在焊缝方向上求均值,并除以固有应变的分布面积AW,可以得到平均纵向固有应变εL和平均横向固有应变εT。
| Cross section position x/mm | Sum of natural strain/10-5 mm2 |
| 1 | 87 |
| 19 | 53 |
| 36 | 102 |
| 56 | 105 |
| 81 | 108 |
| 98 | 114 |
总体焊缝长度上平均固有应变εa的计算公式:
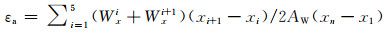
|
(2) |
计算得出在此焊接参数下平均纵向固有应变εL为-1.68×10-3,同理统计并计算得出其平均横向固有应变εT为-2.95×10-2。
2.3 失稳变形有限元分析判据超薄板的焊后失稳变形直接来源于超薄板平面内存在于焊缝区域外的与拉应力平衡的残余压应力[16],该应力的大小取决于焊缝及附近的残余压缩塑性变形量。特征值屈曲分析通过施加位移约束等效载荷,计算薄板刚度矩阵奇异时的特征值,并获得各阶屈曲模态的临界失稳载荷。适用于计算理想弹性薄板的理论屈曲强度。
采用ABAQUS特征值屈曲求解器(buckle),在模型相应区域施加计算得到的固有应变,进行屈曲变形计算。以模型总刚度矩阵进行失稳判断,载荷P按一定的比例因子λ增加,即P=λPapp(Papp为残余塑性应变等效热载荷),此时第N个应力矩阵也按同一比例因子增大,即KN=λK1,如在载荷第n级时|K|n为正,n+1级时|K|n+1为负,那么在此级处有Δσ载荷增加的区间内存在着屈曲点,即|K|=0的点。此时有:
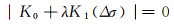
|
(3) |
稳定平衡位移与P成正比,故当λ到达临界值时,P也到达了临界载荷,此时薄板开始向失稳平衡转变,对应每一个特征值都代表了薄板结构的一种失稳变形状态,相应的屈曲虚位移矩阵{ψ}i满足以下条件[17]:
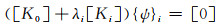
|
(4) |
根据上式,通过有限元计算求出最小特征值λ=λcr。若λcr小于1则可判定系统发生失稳变形[18]。通常认为纵向固有应变是屈曲失稳的主要原因,即可求出临界载荷Pcr:
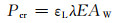
|
(5) |
式中:E为材料的弹性模量,取常温1.95×105 MPa。
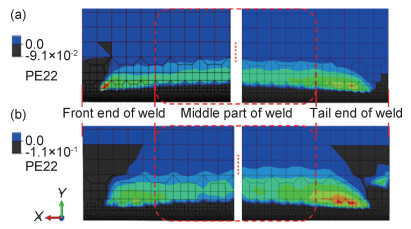
3 计算结果与验证 3.1 特征值屈曲模拟与实测结果的对比对比较低热输入(100 W)和较高热输入(140 W)激光焊后的固有应变的分布,以及平均固有应变值的计算结果,发现相对于较低热输入而言,较高热输入下虽然固有应变的分布区域较宽,但平均纵向塑性应变的数值较为接近(约为-1.56×10-3)。两种热输入的主要差别体现在高热输入下横向塑性应变的平均值较大(-4.54×10-2),而且分布区域有明显的拓宽,小功率与大功率下横向残余塑性应变在焊缝与邻近区域的分布状况(薄板背面边界处与部分中部区域)如图 6所示,热输入较小时,横向塑性应变主要集中在试板的焊缝中心位置,如图 6(a)所示;热输入条件较大时,横向塑性变形除了在焊缝中心附近之外,还在试板的起始端和末尾段的宽度方向上有较大的分布,如图 6(b)所示。
|
图 6 不同热输入下焊后横向残余塑性应变分布区域与大小的对比 (a)低热输入;(b)高热输入 Fig. 6 Comparison of distribution region and size of transverse residual plastic strain after welding under different heat input (a)low heat input; (b)high heat input |
由此,在进行屈曲分析时,在如图 7所示的区域中施加固有应变数值。不同的热输入条件对比通过施加不同的固有应变数值来区分:在较高的热输入条件下,施加包括纵向和横向在内双向固有应变,在较低的热输入条件下,仅施加纵向固有应变,与图 6中的结果相对应。

|
图 7 横向塑性应变的固有应变加载方式 Fig. 7 Inherent strain loading mode considering transverse plastic strain |
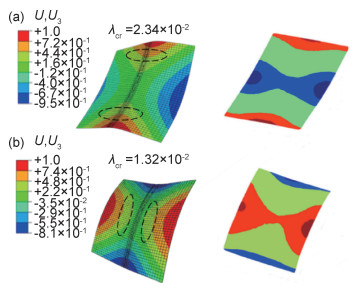
两种加载方式的计算结果如图 8所示。在考虑双向塑性应变条件下,形成的变形形态为两端翘起“横凸纵凹”的马鞍状变形(图 8(a));在仅考虑纵向塑性应变条件下,形成平行焊缝两边中部翘起“横凹纵凸”的反马鞍状变形形态(图 8(b))。
|
图 8 两种普遍的屈曲变形模态 (a)马鞍状变形(高热输入条件,施加双向塑性应变);(b)反马鞍状变形(低热输入条件,仅施加纵向塑性应变) Fig. 8 Two common modes of buckling deformation (a)saddle deformation(high heat input, biaxial plastic strain); (b)reverse saddle deformation(low heat input, longitudinal plastic strain) |
为了验证模型的准确性,研究中测量了不同热输入条件下的焊接变形形态。结果如图 8(a)和(b)的右侧图所示。在较高热输入条件下,横向塑性变形和纵向塑性变形的数值均较大,形成的焊接变形为马鞍状变形;在较低热输入下,以纵向塑性变形为主,变形形态为反马鞍形状。由此可见,通过调整固有应变加载区,并考虑到横向塑性应变作用的特征值屈曲分析可获得焊后由于发生失稳而出现的较为普遍的屈曲模态,该模拟方法能够预测结构的可能变形模式。
分析认为,当试板局部区域受到的压应力超过临界失稳载荷时,试板发生朝向面外的失稳变形[19]。由于试板的底部有垫板作为支撑,因此该区域的面外变形表现为向上凸起。
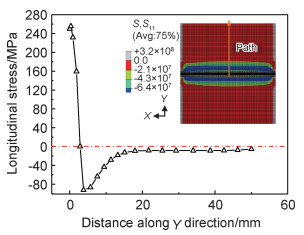
当热输入较小时,试板焊缝附近主要发生了纵向压缩塑性变形,施加在图 7中用橙色标识出的区域,在此情况下,在试样长度方向(X向)的中截面上,焊缝及附近区域受到纵向拉应力,远离焊缝区域受到纵向压应力,在离焊缝中心线约3.79 mm处,纵向压应力值最大,面外变形起始阶段纵向应力的分布如图 9所示。由此,在纵向压应力相对较大的区域,容易发生向上凸起的面外变形,即图 8(b)中的云图为黄色的区域(虚线框处)向上的凸起变形。所以,在试样长度方向(X向)的中截面上,发生两端向上凸起的角变形。
|
图 9 低热输入条件下试样长度方向(X向)的中截面上纵向应力分布示意图 Fig. 9 Longitudinal stress distribution on the middle section of the X direction of the specimen(low heat input) |
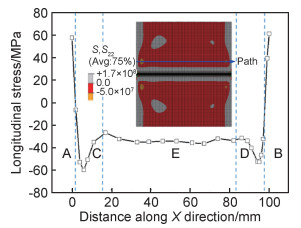
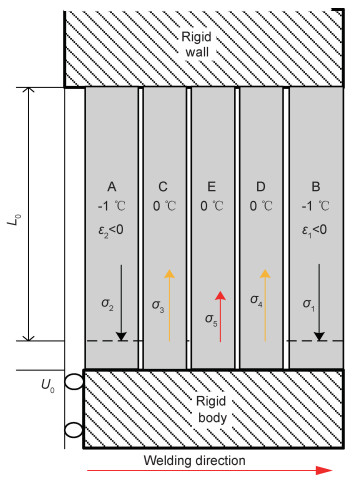
当热输入较大时,横向塑性应变的数值较大,已不可忽略,因此,在图 7中用橙色标识出的区域内同时施加纵向和横向压缩塑性应变。在此情况下,在试板的两端位置(x=0和L0的附近区域),施加横向压缩塑性应变处受到横向拉应力,远离两端的位置受到横向压应力,在X方向坐标为5 mm时,横向压应力值最大,面外变形起始阶段横向应力的分布如图 10所示。由此,在横向压应力最大的区域,容易发生向上凸起的面外变形,即如图 8(a)中的云图为黄色的区域向上的凸起变形。所以,在试样长度方向(X向)的横截面上,发生两端向上凸起的角变形,发现其横向应力的分布在焊缝长度方向上可以大致分为A~E 5个区域。图 11给出了高热输入下薄板的变形机制,A~E为理想化的金属杆,对A, B施加冷源使其收缩,发生位移U。但由于C, D, E的抵抗刚体板运动作用,使A, B受到拉应力作用,而C, D, E此时也会受到相应的压应力作用,使整体截面力平衡。同时由于C, D所受压应力较大,相应区域会发生明显的面外大变形。
|
图 10 高热输入条件下试样长度方向(X向)上横向应力分布示意图 Fig. 10 Transverse stress distribution on the X direction of the specimen(high heat input) |
|
图 11 高热输入焊后薄板变形机制 Fig. 11 Deformation mechanism of thin plate after high heat input welding |
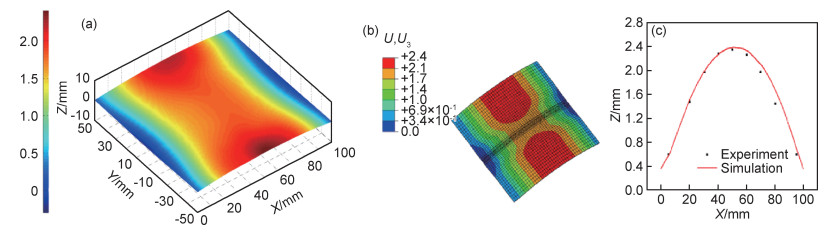
以特征值分析的变形模态作为初始的变形趋势引入后屈曲分析,获得薄板在发生屈曲后的载荷与实际位移的响应方式[20]。功率100 W、焊接速率为20 mm/s条件下,尺寸为100 mm×100 mm试样的后屈曲变形模拟与实验结果对比如图 12所示。图 12(a)为变形测量云图,图 12(b)为数值模拟云图,图 12(c)为数值模拟和实验结果沿着Path2(图 3)的Z方向变形数据比较,从图中可以看出两者在整体变形分布趋势上相同,数值吻合良好。
|
图 12 薄板试样的变形测量与模拟结果对比(P=100 W, v=200 mm/s) (a)测量结果;(b)模拟结果;(c)沿path2的变形测量结果 Fig. 12 Comparison of deformation measurement and simulation results(P=100 W, v=200 mm/s) (a)measurement results; (b)simulation results; (c)deformation measurement results along path2 |
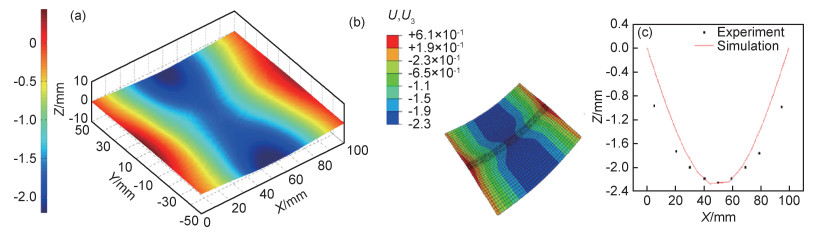
相似,比较了功率为140 W,焊接速率为20 mm/s,尺寸为100 mm×100 mm试样后屈曲变形数值模拟与实验结果,如图 13所示。从图中可以看出此参数下超薄板的变形方向与图 12的变形方向正好相反。数值模拟结果与测量结果趋势相同,数值相当。由此表明,通过后屈曲分析,可以获得超薄板激光焊接头在不同热输入条件下的焊接变形量。
|
图 13 薄板试样的变形测量与模拟结果对比(P=140 W, v=200 mm/s) (a)测量结果;(b)模拟结果;(c)沿path2的变形测量结果 Fig. 13 Comparison of deformation measurement and simulation results (P=140 W, v=200 mm/s) (a)measurement results; (b)simulation results; (c)deformation measurement results along path2 |
对于超薄板焊接接头而言,在厚度确定的条件下,板的尺寸通过影响其刚度,决定了其抵抗失稳变形的阻力Pcr的大小。在屈曲分析模型的基础上,采用特征值屈曲分析方法研究不同板长对薄板屈曲变形的影响。首先,在固定板宽为100 mm,板厚为0.07 mm和热输入条件不变的情况下,计算不同焊缝方向板长薄板的屈曲特征值,取屈曲分析的第一阶模态进行对比,如表 4所示。
| Plate length/mm | First order eigenvalue | Critical buckling load/N |
| 36 | -4.96×10-3 | 0.89 |
| 84 | 2.4×10-2 | 4.29 |
| 100 | 1.64×10-2 | 2.93 |
| 160 | 8.4×10-3 | 1.50 |
| 200 | 7.1×10-3 | 1.27 |
计算结果显示,随着板长的增加,平行于焊缝方向的刚度不断降低,导致焊后失稳临界载荷越来越小。由此,可以通过在薄板内部残余压应力较大的位置加装平行焊缝方向的肋板加强筋,以加大板材的局部横截面积,提升焊缝方向的刚度,从而提高临界失稳载荷,抑制屈曲变形的发生。
4.2 薄板宽度对屈曲特征值的影响研究不同板宽对薄板屈曲变形的影响,在固定板长为100 mm,板厚为0.07 mm和热输入条件不变的情况下,计算不同宽度薄板所对应的屈曲特征值,同样取屈曲分析的第一阶模态进行对比分析。
| Plate width/mm | First order eigenvalue | Critical buckling load/N |
| 50 | 1.86×10-2 | 3.32 |
| 76 | 1.48×10-2 | 2.65 |
| 124 | 2×10-2 | 3.58 |
| 140 | 2.23×10-2 | 3.97 |
| 189 | 2.68×10-2 | 4.79 |
分析计算结果可以发现,随着板宽的增加(50~76 mm),此时薄板的面积增大,整体刚度降低会使临界失稳载荷减小。当板宽超过76 mm后,平行焊缝方向的刚度增加的影响超过面积增大导致的刚度减小带来的影响,板宽的增加使薄板的整体失稳临界载荷又增大。由此,通过增加板宽,有利于增加结构的稳定性,减小失稳变形的可能性。
4.3 薄板厚度对屈曲特征值的影响研究板厚度增大对100 mm边长的正方形薄板焊接屈曲变形带来的影响,在其他条件与0.07 mm厚板模型保持相同的情况下,计算更厚的3个薄板模型所对应的屈曲特征值,同样取屈曲分析的第一阶模态进行对比分析。
| Plate thickness/mm | First order eigenvalue | Critical buckling load /N |
| 0.15 | 7.53×10-2 | 13.44 |
| 0.3 | 3.14×10-1 | 56.05 |
| 0.6 | 1.2 | 214.20 |
对比计算结果,可以发现随着薄板厚度的增大,临界屈曲载荷显著增大,从厚度为0.07 mm的2.93 N增至厚度为0.6 mm的214.2 N。在厚度增加到0.6 mm时,第一阶屈曲特征值已经超过1,说明在理想条件下薄板发生面外屈曲变形的可能性较小。分析认为,薄板厚度的增大,提升了结构的刚度,从而降低了焊接结构发生屈曲变形的可能性。
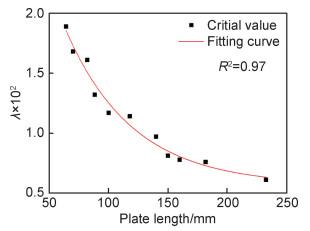
4.4 薄板整体尺寸对屈曲特征值的影响在长宽比不变(1:1)的情况下,薄板的整体尺寸越小,其抵抗失稳变形的能力越强。研究薄板尺寸对临界失稳载荷的影响规律,按比例改变长宽建立不同尺寸的薄板模型,模型尺寸由64 mm×64 mm逐渐增至233 mm×233 mm,在相同的条件下进行特征值屈曲分析,取第一阶正特征值λcr计算,拟合λ(λcr×100)与板长的关系如图 14所示。可以看出薄板的临界失稳载荷随着尺寸的增大而减小,下降速度逐渐趋于缓慢。拟合结果如下式:
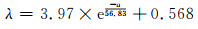
|
(6) |
|
图 14 特征值与板长的关系(特征值屈曲分析) Fig. 14 Relationship between eigenvalues and plate length (eigenvalue buckling analysis) |
根据数值模拟得出的薄板屈曲变形规律,对于存在薄板焊接结构的构件,为了防止薄板发生较大的屈曲失稳现象,在厚度不变的前提下,在设计时应尽量减小所用薄板的尺寸。
5 结论(1) 通过对超薄板激光焊接过程的热力耦合分析,获得固有应变的分布,进而以固有应变为载荷,开展超薄板的焊后屈曲分析,可获得超薄板焊接过程的屈曲模态和失稳变形量。数值分析的失稳变形量与实验测试结果趋势相同,数值接近,由此表明基于固有应变建立的模型可以用于超薄板激光焊过程的屈曲分析。
(2) 薄板尺寸是影响屈曲特征值的重要因素。当薄板长宽比为1:1时,随着薄板整体尺寸的增大,其最大临界屈曲失稳载荷逐渐减小,可采用特征值公式λ=3.97×e-a/56.83+0.568进行拟合。
(3) 在较低热输入下,超薄金属板产生凹-凸变形,在较高热输入下产生凸-凹变形。从屈曲分析的角度看,其主要原因是:在较低热输入下,超薄板内以纵向塑性应变作用为主,在纵向压应力整体偏大的区域,容易发生向上凸起的面外变形。当热输入较大时,超薄板内横向塑性应变的数值较大,已不可忽略,在横向压应力最大的区域,容易发生向上凸起的面外变形。
| [1] |
郭玉泉.核主泵屏蔽套用薄板激光焊接变形预测及调控[D].大连: 大连理工大学, 2014. GUO Y Q. Prediction and control of laser welding deformation of thin plate shielded by nuclear main pump[D]. Dalian: Dalian University of Technology, 2014. |
| [2] |
王健超, 张瑄珺, 张伟, 等. 激光塑料焊接工艺研究与数值模拟分析[J]. 应用激光, 2014, 34(3): 233-237. WANG J C, ZHANG X J, ZHANG W, et al. Research and numerical simulation analysis of laser plastic welding process[J]. Applied Laser, 2014, 34(3): 233-237. |
| [3] |
阚玉艳.超薄不锈钢板激光焊接变形预测建模研究[D].上海: 上海交通大学, 2014. KAN Y Y. Study on prediction modeling of laser welding deformation of ultra-thin stainless steel plate[D]. Shanghai: Shanghai Jiaotong University, 2014. |
| [4] |
毛志涛.初期变形和拘束条件对薄板焊接接头及结构焊接变形影响的研究[D].重庆: 重庆大学, 2017. MAO Z T. Study on the influence of initial deformation and restraint conditions on welding deformation of thin plate welded joints and structures[D]. Chongqing: Chongqing University, 2017. |
| [5] |
DENG D, ZHOU Y, BI T, et al. Experimental and numerical investigations of welding distortion induced by CO2 gas arc welding in thin-plate bead-on joints[J]. Materials & Design, 2013, 52(24): 720-729. |
| [6] |
WANG J, YIN X, MURAKAWA H. Experimental and computational analysis of residual buckling distortion of bead-on-plate welded joint[J]. Journal of Materials Processing Technology, 2013, 213(8): 1447-1458. DOI:10.1016/j.jmatprotec.2013.02.009 |
| [7] |
叶延洪, 何静, 蔡建鹏, 等. 6061-T651铝合金薄板接头的焊接变形[J]. 中国有色金属学报, 2014, 24(10): 2435-2442. YE Y H, HE J, CAI J P, et al. Welding deformation of 6061-T651 aluminum alloy sheet joint[J]. Chinese Journal of Nonferrous Metals, 2014, 24(10): 2435-2442. |
| [8] |
HUANG H, WANG J, LI L, et al. Prediction of laser welding induced deformation in thin sheets by efficient numerical modeling[J]. Journal of Materials Processing Technology, 2016, 227: 117-128. DOI:10.1016/j.jmatprotec.2015.08.002 |
| [9] |
梁伟, 周亮, 孙晓露, 等. 采用固有应变法预测超薄板的焊接变形[J]. 焊接学报, 2017, 38(3): 103-106. LIANG W, ZHOU L, SUN X L, et al. The inherent strain method of predicting the welding deformation of ultra-thin plate[J]. Welding Journal, 2017, 38(3): 103-106. |
| [10] |
FAN Y, CHEN Z, ZHANG C H, et al. A comparison of microstructure and mechanical properties of welded thin Ti6Al4V with three different types of laser[J]. Materials Research Innovations, 2015, 19(Suppl 4): 187-192. |
| [11] |
YI P, DU X, KAN Y, et al. Modeling and experimental study of laser welding distortion of thin metallic bipolar plates for PEM fuel cells[J]. International Journal of Hydrogen Energy, 2015, 40(14): 4850-4860. DOI:10.1016/j.ijhydene.2015.02.025 |
| [12] |
王波, 舒林森. 约束状态对SUS304薄钢板单面激光焊接变形的影响[J]. 热加工工艺, 2019, 48(7): 203-207. WANG B, SHU L S. Effect of constraint state on single-side laser welding deformation of SUS304 thin steel plate[J]. Hot Working Technology, 2019, 48(7): 203-207. |
| [13] |
高辰.基于固有应变法的舰船标准平台焊接失稳变形预测研究[D].镇江: 江苏科技大学, 2017. GAO C. Study on prediction of welding instability deformation of warship standard platform based on inherent strain method[D]. Zhenjiang: Jiangsu University of Science and Technology, 2017. |
| [14] |
闫俊霞, 霍立兴, 张玉凤, 等. 焊接薄板失稳变形预测方法[J]. 焊接学报, 2005(6): 50-53. YAN J X, HUO L X, ZHANG Y F, et al. Prediction method of instability deformation of welded thin plate[J]. Welding Journal, 2005(6): 50-53. DOI:10.3321/j.issn:0253-360X.2005.06.013 |
| [15] |
冯超, 梁晋, 郭楠, 等. 板料焊接屈曲变形测量[J]. 焊接学报, 2016, 37(7): 61-64. FENG C, LIANG J, GUO N, et al. Measurement of buckling deformation in sheet metal welding[J]. Welding Journal, 2016, 37(7): 61-64. |
| [16] |
郭楠, 梁晋, 龚春园, 等. 在线测量薄板焊缝区的变形[J]. 焊接学报, 2016(8): 1-4. GUO N, LIANG J, GONG C Y, et al. On-line measurement of the deformation in the weld zone of thin plate[J]. Welding Journal, 2016(8): 1-4. |
| [17] |
WANG J, RASHED S, MURAKAWA H. Mechanism investigation of welding induced buckling using inherent deformation method[J]. Thin-Walled Structures, 2014, 80: 103-119. DOI:10.1016/j.tws.2014.03.003 |
| [18] |
LIANG W, MURAKAWA H, DENG D. Estimating inherent deformation in thin-plate Al-alloy joint by means of inverse analysis with the help of cutting technique[J]. Advances in Engineering Software, 2016, 99: 89-99. DOI:10.1016/j.advengsoft.2016.05.003 |
| [19] |
王江超. 薄板船体结构焊接失稳变形的数值分析进展[J]. 造船技术, 2017(2): 73-78. WANG J C. Progress in numerical analysis of welding instability deformation of thin plate hull structures[J]. Shipbuilding Technology, 2017(2): 73-78. |
| [20] |
李欣涛, 龙连春. 局部激光辐照下薄板结构的屈曲承载力分析[J]. 高压物理学报, 2016, 30(2): 142-148. LI X T, LONG L C. Analysis of buckling bearing capacity of thin plate structures irradiated by local laser[J]. Journal of High Pressure Physics, 2016, 30(2): 142-148. |
 2020, Vol. 48
2020, Vol. 48


