文章信息
- 廖向娜, 贺雍律, 张鉴炜, 鞠苏, 江大志, 刘佳音, 刘钧
- LIAO Xiang-na, HE Yong-lyu, ZHANG Jian-wei, JU Su, JIANG Da-zhi, LIU Jia-yin, LIU Jun
- CNTs-纤维增强树脂基复合材料纳米-介观尺度数值模拟研究进展
- Research progress in nano-meso scale modelling of carbon nanotube reinforced FRP composites
- 材料工程, 2020, 48(12): 1-11
- Journal of Materials Engineering, 2020, 48(12): 1-11.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2020.000154
-
文章历史
- 收稿日期: 2020-02-24
- 修订日期: 2020-06-20
2. 中山大学 材料学院, 广州 510006
2. School of Materials, Sun Yat-sen University, Guangzhou 510006, China
碳纳米管(CNTs)是一类轻质高强[1]的一维管状纳米材料,其尺寸小(径向尺寸纳米量级、轴向尺寸微米量级)、密度低、强度高,引入复合材料后不会显著增加结构质量,基本不会影响纤维的排布及含量,是一种理想的复合材料增强相。
目前已经有实验表明[2-6],在传统碳纤维复合材料的聚合物基体中分散适量的CNTs可以有效提高复合材料的力学性能,亦可赋予传统碳纤维复合材料在宏观尺度下所不具备的功能特性,拓展其应用范围。研究者们为将CNTs引入碳纤维复合材料中开发了多种技术途径,包括CNTs和树脂共混[2-3]、CNTs原位生长/化学接枝[5-6]、阵列插层[7]、巴基纸增强[8]等,但上述技术途径往往无法得到预期的CNTs增强效果[8-9]。
CNTs比表面积高(达1300 m2/g)[10],长径比大(100~5000)[11],加入复合材料时会出现团聚现象[12-13],无法充分发挥CNTs的增强效果。CNTs本征结构特征,如直径、长度、曲直度、管壁结构、管壁缺陷等因素以及CNTs化学性质,如表面化学性能、表面官能团等因素对纳米复合材料力学性能和失效模式的影响机制复杂。Gojny等[11]指出CNTs的比表面积和分散性之间有联系,比表面积越大,分散性越差,不同的表面功能化情况也可以显著引起分散性的变化;此外,从CNTs/树脂微观结构角度出发,CNTs的增强效果强烈依赖于其在基体中的空间位置和取向分布(CNTs网络的形态)[14]。因此,在CNTs/树脂基复合材料中,多因素影响的复杂性非常突出,为基于实验方法的研究与分析带来很大难度[15]。在目前实验制备与表征技术不完善的情况下,通过数值模拟方法来研究CNTs对树脂的增强效果以及增强机理是一种可行,且更为快捷、有效的途径[9]。
通过模型建立和数值模拟获得准确、系统的CNTs-纤维增强树脂基复合材料性能评价机制尤为必要。因此,本文将从CNTs增强树脂基复合材料的数值模拟研究尺度、数值模拟方法、CNTs对复合材料力学性能影响规律三方面,综述目前CNTs-纤维增强树脂基复合材料纳米-介观尺度数值模拟研究进展。
1 纳米-介观尺度模型CNTs-纤维增强树脂基复合材料是多尺度、多相材料,具体来说包括:CNTs增强相(纳米-微米尺度);纤维增强相(微米-宏观尺度);基体相;基体与CNTs、纤维界面相。在不考虑CNTs与纤维相互作用的情况下,CNTs对复合材料的影响主要体现在两个方面:(1)CNTs对树脂基体的增强作用。CNTs模量在270~950 GPa之间,添加到纤维复合材料中后,可以对性能相对薄弱的树脂区域进行增强。Gojny等[3]观察到CNTs通过裂纹桥联[16]的方式桥联环氧树脂基体中宽度为几微米的裂纹,从而增强树脂基体。此外,在CNTs/树脂基体界面相互作用的主导下,CNTs可以通过脱粘或者拔出的方式增强树脂基体。Needleman等[17]分析了界面强度变化对复合材料应力-应变响应的影响,并指出CNTs/树脂界面的存在可以增加复合材料的刚度,但同时也会促进CNTs脱粘,最终降低复合材料应力承载能力。(2)CNTs对周边纤维及基体应力分布的影响。如图 1[18]所示,研究者们构建了五种具有明显区别的CNTs分布方式模型,发现除了单个CNTs产生的局部应力变化外,不同分布方式的CNTs可作为微观实体共同作用,产生微观级别的应力分布影响。比如,在CNTs浓度高于周围材料的团聚体中,CNTs团块开始表现为微尺度的刚性颗粒,在纤维表面附近产生高的微观尺度的应力集中。
目前基于CNTs/基体界面对复合材料增强机制的研究主要针对CNTs脱粘和拔出[17]、裂纹桥联[16]等,基于CNTs在树脂中的分布状态对复合材料增强机制的研究主要针对损伤扩散[19]、裂纹偏转[20]、裂纹钉扎和断裂[21-22]等。CNTs脱粘和拔出、裂纹桥联是纳米尺度增强机制。介观尺度下CNTs的增强效果依赖于CNTs的空间形态(空间位置和排列方向)。为了充分利用纳米填料的增强效应,需要从纳米尺度出发,并辅之以合适的模型来预测复合材料的性能,以便为复合材料的特定应用设计提供解决方案。随着研究的进一步深入,Liu等[14]发现,CNTs的真正增强能力在于介观尺度和纳米尺度的复合激活作用,而且此种复合作用对CNTs空间分布形态和CNTs/基体界面的性质有复杂的依赖关系。因此,在考虑CNTs-纤维复合材料数值模拟时,我们应重点考察CNTs的本征性能、CNTs/基体界面性能以及CNTs在基体中的分布状态等三个关键要素,建立CNTs-纤维增强复合材料纳米-介观尺度模型。
2 纳米-介观尺度模型数值模拟方法从CNTs对复合材料性能影响的角度出发进行数值模拟研究时应建立纳米-介观尺度模型,即建立的模型应该反映纳米、介观尺度上的材料特性,能达成这一目标的建模方法目前主要包括三类,分别是分子动力学方法、有限元方法和解析法。
2.1 分子动力学方法分子动力学方法是一种基于计算机模拟的技术手段,可以准确预测在一定时间跨度下的原子、分子、晶粒等的相互作用,从而给出体系相关的物理性能(电、磁、热相关性能、聚合物玻璃化转变温度等)。具体来说,它可以基于原子位置、速度、力等信息计算材料宏观性能(压力、能量、热容、模量等)。分子动力学模拟主要包含三个环节,即初始条件、势函数以及基于经典牛顿力学运动方程的系统演进过程。分子动力学方法通过采用离散的方法计算固定单元内粒子的功,最终将许多化学物理相互作用性质如界面弹性性质、界面能等评估出来。这些界面性质和界面能对于复合材料整体性能的改善具有指导性作用。Quaresimin等[23]认为分子动力学方法是解决纳米复合材料性能评估问题的有效方法。具体来说,分子动力学方法可以从分子间作用力角度,有效预测不同CNTs/基体分子构型下,CNTs、基体本征强度,以及CNTs-基体间界面相互作用等实验无法或无法准确表征的参量。
Li等[24]分别建立了纯交联环氧树脂和(6,6)CNTs增强树脂复合材料的分子模型(图 2)。通过去除两种分子结构中相应区域的原子和化学键,在两种结构中都形成了宽度为0.3 nm、长度为1.8 nm的中心单侧裂纹。基于上述两种分子模型,采用恒应变法模拟CNTs/环氧复合材料的断裂性能。Zhang等[25]将两个管间桥联的单壁CNTs嵌在聚乙烯(PE)基体中,并通过分子动力学方法研究CNTs从PE基体中的拔出现象。Alian等[26]采用分子动力学方法解释了CNTs波纹度和团聚对纳米复合材料界面强度及其载荷传递能力的影响。波纹度的影响通过模拟不同曲率的CNTs来考虑,团聚的影响则通过模拟不同尺寸的纳米管束来考虑。Frankland等[27]建立了连续的长CNTs复合材料和不连续的短CNTs复合材料模型,每个复合材料的单元尺寸为5 nm×5 nm×10 nm。在两个分子模型上分别施加横向载荷和纵向载荷后,通过应力-应变响应来观察两种CNTs对聚合物基体的增强效果。在应变模拟中,作者指出高应变速率是分子动力学仿真的固有特性,通常包含10-12~10-9s时间尺度上的动态信息;在应力模拟中,作者将连续水平的应力张量计算公式(式(1))扩展到原子水平,总内能E可以表示为单个原子的能量之和。
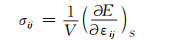
|
(1) |
式中:V是固体的体积;E是总内能,εij是应变张量,下标S表示恒定熵。应变的施加通过在变形方向上均匀拓展复合材料单元的尺寸并重新校正原子的坐标以适应新的复合材料单元尺寸来完成。在模拟中,作者每增加2%的应变之后,将系统松弛2×10-12 s,然后在10×10-12 s的间隔内平均系统上的应力。对于每种复合材料单元,在72×10-12 s的时间内施加六次增量为2%的应变,相应的应变速率为1×1010 s-1。分子动力学模拟中,应变速率与实际应变速率相比通常高8~10个数量级,超高应变速率对复合材料力学性能的预测尤其是强度性能会带来显著影响,其具体影响规律与材料属性相关。
分子动力学方法虽然能够预测CNTs与基体之间的分子相互作用,但仅限于非常小的几何尺度(10-10~10-9 m)和时间跨度(10-15~10-9 s)。此外,由于计算力的制约,原子量为数亿的复合材料模型在分子动力学模拟中是不可行的。基于分子动力学的此种缺陷,研究者们提出了“粗颗粒模型(coarse grained(CG) simulations)”[28-30]。该模型的原理是将一组原子映射到一个粗颗粒(CG bead)上,在保持原子系统分子细节的同时,拓宽可仿真的时间跨度和模型几何尺度。在文献[30]中,研究者采用基于CG模型的J积分计算方法(J-integral)成功预测了CNTs/PMMA复合材料的弹塑性性能。该方法超越了传统分子模拟的仿真能力,与全原子体系相比,能够大大增加可计算的尺度。但CG模型在简化全原子体系过程中也会遇到诸多问题,Duan等[31]证实CNTs/树脂复合材料全原子体系的界面特性与CG体系存在明显的偏差,会对材料力学性能的预测带来影响。他们指出了以下两点区别:(1)CG模型中的界面内聚能明显高于全原子模型,会导致界面载荷传递能力的过高评估;(2)粗粒化程度(degree of coarse graining λ, 相邻两个粗颗粒间的距离,单位为1 nm)的选择也会对CG模型中界面载荷传递能力产生影响,当采用不同的λ值来建立CG模型时,与全原子体系相比,纳米复合材料的力学性能预测偏差较大。
2.2 有限元方法有限元方法是一种常用的高效能数值计算方法。科学计算领域常常需要求解各类微分方程,而许多微分方程的解析解一般很难得到,使用有限元方法将微分方程离散化后,可以使用计算机辅助求解。有限元方法中的重要步骤是网格划分,该步骤能使模型应用到高度非均质的情况下,能将复杂的非线性应力-应变关系考虑进模型中。
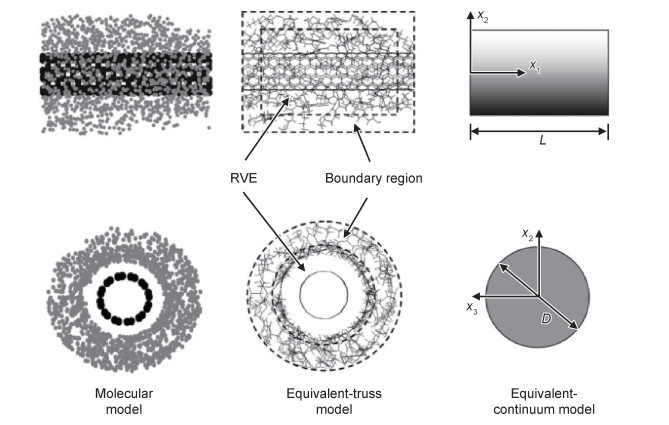
为了将纳米尺度和介观尺度统一起来,从而完成计算结果的有效传递,Odegard等[32]提出可以作为连接分子模型和等效连续体模型中间步骤的等效桁架模型(图 3)。首先,考虑纳米尺度原子的离散性,利用分子动力学模拟确定的原子结构建立纳米管及其邻近聚合物的分子结构模型(图 3左侧)。其次,利用从分子动力学方法模拟得到的平衡分子结构,建立复合材料的等效连续介质模型(图 3右侧),将CNTs、CNTs附近的局部聚合物以及CNTs/聚合物界面等效为有效的连续介质模型。最后,将该连续模型应用于微观力学模型中,通过考虑CNTs排列方式、CNTs类型、CNTs体积分数等因素计算CNTs增强复合材料的特性。从分子模型到等效连续模型,通过建立不连续的、由许多原子组成的代表性体积单元的等效桁架模型来完成(图 3中间)。在相同加载条件下,分子模型的总分子势能与等效桁架的应变能相等。因此在相同加载条件下,将CNTs及其附近聚合物建模为有效连续纤维的等效连续介质模型与分子动力学模型的总应变能也是相等的。该方法全面有效,具有广泛的适用性,适用于既要求原子级描述的准确性又要求连续级模型的通用性的情况下。Jia等[33]采用连续介质力学方法,将CNTs看作薄膜单元用空间中的薄表面来表示,采用轴对称内聚单元(cohesive zone)来定义CNTs与基体界面之间的黏聚区域,从而通过有限元方法模拟单个CNTs从聚合物基体中的拔出过程。内聚单元模型(cohesive zone model)[34]是研究由于裂纹或脱粘扩展引起的破坏的常用方法,被证明可以与Cooper等[35]的实验结果很好地拟合。
中间均质化就是采用具有均质性能的有效材料(如连续体实心梁、连续体实心壳)来代替CNTs增强区域的方法。由于该方法忽略了CNTs及其界面区域应力状态,从而无法捕获纤维和CNTs之间真实的应力传递行为。比利时的Romanov团队基于上述问题,提出了一种新的基于有限元方法的ER(embedded region)技术[18, 36-38]来预测CNTs增强纤维复合材料的应力-应变响应。该方法克服了传统的跨尺度模拟中,在模拟纳米尺度CNTs与介观尺度碳纤维时由于网格不适配而必须分次模拟再提取参数均质化的过程,能在一次计算中完成跨尺度计算,有效地提高了计算准确性,节省了计算步骤与时间。ER技术(亦称EE技术)是基于独立生成的有限元网格之间相互作用的技术,两个有限元网格是独立创建的:主区域网格(基体)和嵌入区域网格(单个CNTs)。在有限元网格划分的过程中,分先后两步独立地划分CNTs以及周边基体。在计算过程中,将和CNTs临近的基体单元节点位移进行线性插值近似,并赋给临近CNTs节点,从而达到CNTs与基体的耦合。比如,CNTs接枝在纤维上对复合材料强度和韧性影响的研究中[39],纤维和CNTs依据其真实尺寸建模,基体采用ER技术进行模型建立和网格划分。CNTs的外层定义为嵌入区域,基体的外层定义为主区域,随后将嵌入域的节点位移从主域的节点位移中进行插值近似,使两个区域耦合在一起。
ER技术的有效性已经得到了系统的验证[40-41],并应用于分析CNTs脱附对CNTs复合材料性能的影响[14]。Liu等[40]指出EE-CZM方法的准确性依赖于纤维、界面和基体的网格尺寸大小,并就EE-CZM方法对网格尺寸的敏感性进行评估。评估结果认为,当纤维的网格尺寸不超过纤维半径的一倍,基体的网格尺寸不超过纤维半径的12倍时,建模结果足够准确,即可以与有限元建模结果吻合。Romanov等[36]采用ER技术模拟生长在纤维上的CNTs。比较高密度CNTs、低密度CNTs以及无CNTs 3种模型后得知生长在纤维上的CNTs能够有效地抑制纤维/基体界面的应力集中, 并且认为此现象是CNTs引入的纳米尺度异质性和纤维形成的微观结构之间的相互影响。Rai等[42]采用ER技术研究无规分散、团聚体两种CNTs形态下纳米复合材料的载荷转移和损伤效应。将CNTs无规分散、团聚体、质量分数等变量考虑进有限元模型中,发现CNTs周围局部区域的力学响应和复合材料整体的力学响应存在显著差异;团聚体内部会形成无应力区,导致基体与团聚体表面脱粘,从而加速损伤。由此,他们强调了在研究CNTs增强复合材料时需考虑局部力学性能,也强调在CNTs复合材料制备过程中有效分散CNTs的必要性。ER技术在预测复合材料的弹性应力场和刚度的工作中取得了良好的效果[43-44], 但是此种技术由于建模过程中物理界面的缺失而无法模拟界面损伤/脱粘。为此,Liu等[40]将内聚区模型和ER技术结合起来模拟纤维复合材料中的界面损伤,即ER-CZM(embedded region-cohesive zone model)模型。与传统的模型相比,ER-CZM模型把嵌入元素和内聚元素结合在一起,将作为内聚元素的界面层(outer-layer)嵌入模型当中。此外,ER-CZM模型准确地再现了有限元建模的结果,包括纤维中、沿纤维界面、基体中的应力分布,应变能以及纤维复合材料的界面损伤发展。Liu等[45]也将遗传算法与有限元方法结合,提出了一种新的并行双尺度优化方法来设计CNTs的位置和方向,以期获得最佳CNTs空间分布和取向。其中,有限元法用于预测应力场,遗传算法用于生成CNTs网格形态。
2.3 解析法解析法是应用数学推导、演绎去求解数学模型的一类建模方法。在研究复合材料力学性能相关问题时,该方法具有建模简单、计算方便,对研究对象的跨尺度几何特性不敏感等优点,因此得到了广泛的应用[46-49]。较为经典的解析方法有:Halpin-Tsai方法[49]、自洽法及广义自洽法、Mori-Tanaka[50-51]以及Eshelby等效加载理论[52]等。
Blanco等[46]采用纤维桥联的裂纹闭合方法,基于CNTs拔出以及剑鞘滑移模式建立了CNTs Z向层间增韧复合材料层合板的Ⅰ型断裂韧性模型,随着桥连纤维由纳米级增大至微米甚至毫米级别(长径比下降),其增韧效果下降明显,因此该模型侧面反映出CNTs这一纳米尺度纤维对于复合材料增韧的有效性。
Chen等[47]以剪滞理论为基础,假设CNTs和基体都是线弹性的,得出纤维与基体平衡条件下纤维的剪切应力分布公式,也进一步得到了界面脱粘和CNTs断裂两种失效模式下拉力与拉拔位移的曲线关系,并讨论了界面长度和界面强度对增韧效果的影响。
由于CNTs/碳纤维复合材料是一个具有大跨尺度(10-11~10-5 m)、复杂对象(CNTs的复杂形貌、树脂与CNTs界面、纤维排列、基体与纤维界面)的物理模型,一般来说该问题无法采用简单的数学解析式进行精确表达,因此通常会将物理模型简化和近似,并忽略次要变量,比如文献[47]中假设CNTs和基体都是线弹性的,文献[46]中假设将CNTs作为一种刚性长直棒进行处理。显而易见,以上过程不可避免降低了模型的精度,在需要定量分析实际问题时应用空间也较窄。
3 CNTs对FRP复合材料力学性能影响规律CNTs-纤维增强树脂基复合材料作为多尺度复合材料,在纳米-介观尺度模型建立过程中应考察CNTs的本征性能、CNTs/基体界面性能以及CNTs在基体中的分布状态等三个关键要素。因此,研究者们从以上三个关键因素出发,并根据所考察因素的特点选择合适的建模方法(分子动力学方法、解析法、有限元法),已证明CNTs的本征性能(CNTs分子结构、CNTs表面化学)、CNTs的含量和微观分布状态对复合材料的力学性能有影响。
3.1 CNTs本征性能 3.1.1 CNTs分子结构在纳米尺度下,CNTs结构比如管长度[32, 47, 53]、管直径[49]、波纹度[26, 54]、管壁缺陷[55]等,强烈影响着复合材料的整体性能。
Chen等[47, 53]发现,一味地增加CNTs界面长度(实际嵌入长度)不能直接地获得更好的断裂韧性。当CNTs/基体界面仅存在范德华相互作用时,纳米复合材料的失效模式为界面脱粘,随着界面长度的增加,增强效果会逐渐趋于稳定。当CNTs/基体界面相互作用较强时,存在一个CNTs临界长度。当CNTs界面长度小于临界长度时,失效模式为界面脱粘且断裂韧性随着界面长度的增加而增加;当CNTs界面长度超过临界长度时,失效模式转变为CNTs断裂,断裂韧性随着界面长度的增加而下降。由此可知,CNTs界面长度对断裂韧性起着重要作用,而且在实际情况下,CNTs填充物不可能以单个CNTs的形式存在,必然服从统计分布。Menna等[48]指出CNTs界面长度随CNTs长度、方向(相对于力的加载方向)以及每根管的质心在厚度方向的位置而变化,并采用经典的Weibull分布描述了CNTs长度对复合材料层间性能的影响。研究表明,随着CNTs界面长度增加,断裂韧性出现明显上升,达到一个阈值后,其断裂韧性开始下降。
Thostenson等[49]发现,在给定的CNTs直径和体积分数下,随着CNTs长度的增加,弹性模量略有增加;而CNTs直径对复合材料弹性模量的影响最为显著,这就要求在数值计算过程中精确地模拟管径在复合材料中的分布情况。比如,可采用分布函数(洛伦兹分布、高斯分布等)表示管径分布情况,再将其作为影响因子应用到纳米复合材料力学性能的模拟中。多壁CNTs和单壁CNTs的区别仅反映在原子-纳米尺度模型中,纳米-介观尺度有限元模型中,只是考虑与直径相关的计算参数的变化。多壁CNTs由同心的单壁CNTs构成,每个同心层中为共价键,层与层间为范德华相互作用。多壁CNTs的最外层几乎承担了CNTs/基体界面传递的全部载荷,因此在模拟过程中,将多壁CNTs视为有效纤维。有效纤维和多壁CNTs具有相同的变形行为,相同的直径和长度,并将外层承担的所有载荷应用到纳米管的整个截面上。这一处理方法在管外层厚度与管直径之比 < 0.25时均可应用。
Alian等[26]将长度相同,波纹度不同的CNTs嵌入热固性复合材料中,并通过拉拔实验来评估界面剪切强度。弯曲CNTs的拉拔力明显高于直的CNTs,且随着CNTs波纹度的增加进一步增大。对于直的CNTs,施加的拉拔力只负责克服CNTs原子与周围聚合物分子之间的非键合相互作用。然而,对于弯曲纳米管,还需要在开始阶段,克服弯曲纳米管对形状变化的阻力,以及伴随而来的CNTs势能的变化。也就是说,CNTs在拉直过程中消耗了额外的拉出能量。
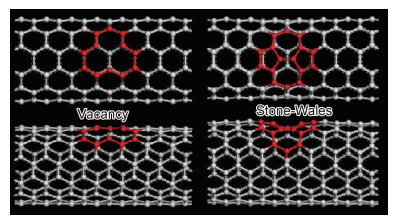
由于计算量和建模可行性的影响,多数研究认为CNTs是没有缺陷的,导致了实验结果与数值模拟之间的偏差。CNTs缺陷包括空位缺陷、SW缺陷等(图 4),空位缺陷是由于管壁上原子缺失而形成的,SW缺陷是CNTs中两个相邻碳原子的拓扑90°键旋转形成的。其中,受到广泛关注的是空位缺陷。Palacios等[56]以CNTs增强聚合物中有5%原子空位的(16,0)单壁CNTs为研究对象,发现纵向弹性模量随着聚合物中原子空位的存在而降低。缺陷使得CNTs中引入了孔洞和间隙,从而形成失效起始点,降低复合材料的力学性能。而Sharma等[57]以含有1个缺陷的(4, 4)单壁CNTs-聚丙烯复合材料为对象发现随着人为诱导的SW缺陷和空位缺陷数量的增加,CNTs的弹性模量均降低,即SWCNT结构中包含SW/空位缺陷通常会降低其力学性能。但是,随着缺陷CNTs体积分数的增加,复合材料的横观各向同性模量和剪切模量均增加。作者指出这一现象是由于缺陷位点的存在使得CNTs与周围的聚丙烯分子之间的界面强度增加,从而通过更有效的界面应力传递效果延缓了纤维桥联和CNTs脱粘的发生,增强了复合材料的力学性能。
|
图 4 空位缺陷和SW缺陷原理图 Fig. 4 Schematic diagram of vacancy and SW defects |
Chen等[47, 53]认为,一味地增加CNTs/基体界面强度不能直接地获得更好的断裂韧性。当界面强度小于临界界面强度时,失效模式为界面脱粘且断裂韧性随着界面强度的增加而增加;当界面强度超过临界界面强度时,失效模式转变为CNTs断裂,断裂韧性随着界面强度的增加而减小。Kulkarni等[34]研究发现,在CNTs体积分数不变的情况下,纳米复合材料的模量随着界面强度的增加而增加,随后模量的增加速率降低,与Chen等[47, 53]的研究结果类似。作者未指出界面强度的临界值,并认为界面强度的上限对应于聚合物基体向CNTs有良好载荷传递的情况。CNTs增强复合材料的界面强度可以通过调整CNTs表面化学键密度来控制, 也可以通过调整CNTs表面官能团来改变CNTs/基体界面相互作用。Jiang等[58]采用分子动力学方法证明添加CNTs的复合材料的玻璃化温度比添加官能团化CNTs的复合材料的玻璃化温度高,添加羟基化CNTs的复合材料比添加羧基化CNTs的复合材料的玻璃化温度高。这是因为自由的羟基和羧基导致CNTs周围更大的距离和更大的界面,因此官能团化CNTs与聚合物基体之间表面相互作用相对较弱。环氧链段即使在较低温度下也可以改变自己的位置,从而降低玻璃化转变温度。据此,有理由相信,CNTs表面改性可以改变基体与CNTs界面相互作用和界面强度,从而改变CNTs增强复合材料的力学性能。这一方法也在实验中得到了证实[59-60]。Ma等[60]对CNTs进行氨基功能化改性后发现,与原始CNTs相比其具有更高的表面能和更强的环氧润湿性,其功能化过程中附着的胺分子有效地抑制了CNTs在树脂固化过程中的重新团聚。此外,改性后的CNTs通过共价键增强与基体分子间的界面附着力,从而改善了CNTs/环氧复合材料的力学性能。
3.2 CNTs的含量与分布 3.2.1 CNTs的含量与分散情况Kulkarni等[34]提到,在界面强度保持不变的情况下,随着CNTs体积分数的增加,复合材料的弹性模量也在增加。然而,由于范德华相互作用和静电力作用,随着CNTs体积分数的增加,CNTs会团聚, 降低CNTs的分散水平,对纳米复合材料的力学性能起着负面的影响。Alian等[26]用不同直径的直线型纳米束研究团聚尺寸对于界面剪切应力的影响。界面剪切应力与管束中CNTs数量呈非线性关系,随团聚体尺寸的增大,界面剪切应力迅速减小,进一步增加管束的尺寸,界面剪切应力降低速率减慢。这是由于与分散良好的CNTs的总表面积相比,管束的有效面积显著减少,界面性能降低。CNTs块体与周围基体的界面粘接性变差,团聚体因此变成了破坏发生的起始点。Moghadam等[61]采用经典层合板理论对CNTs增强碳纤维复合材料的残余应力进行数值分析,发现CNTs团聚体由于产生应力集中而使残余应力增加,且随着团聚体的增大,这一影响会更加明显。复合材料中CNTs引起了两种类型的应力集中:(1)由于CNTs与周围基体强度的差异,单一的CNTs周围产生了纳米级的应力集中,呈现出急剧的应力梯度; (2)团聚的CNTs作为微观实体,产生了微观尺度的应力集中,影响微观尺度上损害的发生。Romanov等[62]认为在基体和纤维/基体界面上,团聚体导致了较高的应力集中现象,且该现象的严重程度取决于CNTs团聚体的密度和大小,也取决于团聚体的程度(未团聚体、部分团聚体、完全团聚体)。通过3种参数研究证实团聚体密度越大,尺寸越大,团聚程度越大,应力集中的现象就越明显,从而促进复合材料中损坏的产生,均匀分布的CNTs对应力场分布的扰动最小。
目前,研究者们除了关注团聚带来的影响外,一部分研究已经关注到了团聚体形态对于复合材料性能的影响。Alian等[63]首先建立含单个CNTs的代表性体积单元,采用分子动力学方法计算其弹性性能。然后沿用分子动力学的计算结果,采用Mori-Tanaka模型计算CNTs团聚对于纳米复合材料力学性能的影响。在采用Mori-Tanaka模型计算之前,需要先建立微观模型。先将分子动力学几何模型等效为“有效纤维”[64],然后建立微观尺度的纳米复合材料代表性体积单元。该方法存在的一个缺点是,在CNTs模拟过程中,将其等效为笔直的圆柱体,这与CNTs本身的形貌特征相差甚远。Chanteli等[65]利用TexGen软件建立不考虑CNTs/聚合物界面的团聚体单胞,然后利用有限元方法对代表性体积单元进行参数化研究。其参数包括CNTs直径、长度、曲直度、CNTs取向等因素。该方法的弊端有以下两点:(1) CNTs曲直度不符合实际情况,TexGen软件采用类似于正弦函数的方法来表征CNTs的曲直度,与实际曲直度相差甚远; (2) CNTs数量甚少。纳米复合材料中,CNTs的数量是较大的,而且相互缠结,甚至会对相间性能造成很大的影响,这一点也与实际情况相差甚远。建立能够反映团聚体真实存在形态的模型仍是纳米粒子团聚体研究中的一大难点。
3.2.2 CNTs的分布CNTs空间分布对纳米复合材料力学性能的影响是显著的。Romanov等[36]发现生长在纤维上的CNTs可以抑制纤维/基体表面的应力集中。Matveeva等[66]使用ER技术研究碳纤维/环氧单向复合材料中CNTs的存在对纤维/基体界面脱粘的影响。该研究对象包含两种CNTs构型:基体中团聚的CNTs和纤维上生长的CNTs。与没有CNTs的复合材料相比,靠近CNTs团聚体位置的纤维/基体界面存在较高的正应力和剪应力,纤维/基体界面分离也从靠近团聚体的位置开始。当CNTs生长在纤维上时,界面正应力和剪应力普遍降低,正应力沿着界面基本保持不变。破坏同时发生在CNTs周围的小块区域,且沿着界面存在许多各自独立的脱粘位点。CNTs接枝纤维和CNTs沉积在纤维表面对应力分布影响的差异较大,是由于CNTs在纤维表面的定向差异造成的[37],从而肯定了CNTs空间分布对于复合材料内部应力分布的影响是存在的。
Liu等[14]采用EE-CZM方法讨论如图 5所示的3种CNTs分布的应力集中问题。从3种CNTs分布方式的应力-应变曲线可知与无CNTs矩形板(图 5(a))相比,CNTs的加入对应力-应变响应造成了影响,均匀分布CNTs(图 5(b))矩形板的刚度,强度和韧性分别增加了4%,6%,14%;空间优化CNTs(图 5(c))板的刚度,强度和韧性分别增加了8%,90%,277%。进一步研究发现,空间优化CNTs板的应力集中因子与无CNTs分布矩形板和均匀分布CNTs矩形板相比,分别下降了54%和49%,说明优化后的CNTs位置和取向对基体应力集中有明显的抑制作用。另一方面,由于基体中应力集中的减少和应力的重新分布,空间优化CNTs板中出现了与无CNTs板和均匀分布CNTs板中的单一主裂纹不同的弥散微裂纹。微裂纹的存在验证了损伤扩散的存在,损伤扩散过程中伴随着大量的界面脱粘和拔出。多种增韧机制相互作用的情况下,能量耗散显著增加,从而起到增韧的作用。
Liu等[45]结合GA和FEM(genetic algorithm-finiteelement method)分析指出CNTs空间分布的优化在某种程度上等同于局部刚度的优化。虽然CNTs密度相同,但可以通过优化位置和方向使CNTs空间分布发生显著变化。更重要的是,通过优化CNTs位置和方向可以进一步抑制应力集中。此外,通过比较质量分数为0.15%和0.30%CNTs的应力场可知,CNTs含量的增加可以更加有效地抑制应力集中。Nazarenko等[67]同样采用带孔的矩形板模型,保持总体CNTs体积分数不变,改变CNTs在区域Ⅰ和Ⅱ中的分布情况。他们发现,改变板内CNTs的空间分布可以显著降低应力集中水平,且仅通过在孔周围的小区域内调节材料特性,就可以显著改善板中的应力集中程度。带孔的板模型只是研究应力集中程度的实例之一,该模型也可以用于研究CNTs密度分布对结构刚度等的影响。
CNTs微观分布状态对复合材料力学性能有影响,而这种影响的纳米尺度机制以及该影响与材料性能之间的关系尚不明确。Liu等[39]采用并行双尺度模型[14]验证了两个参数(CNTs的拉伸强度和CNTs/基体界面性能)对CNTs接枝效果的影响。双尺度模型中,接枝在纤维上的CNTs呈波纹状径向排列,且局部CNTs的取向与垂直于纤维表面CNTs的方向的偏差不小于10°。通过数值研究可知,要获得高性能的CNTs接枝纤维增强复合材料,CNTs强度的提高比CNTs/基体界面强度的提高更为有效。而其他特性,比如纤维以及CNTs的体积分数,几何参数等对CNTs接枝纤维增强复合材料的影响也有待研究。
4 结束语CNTs作为复合材料增强体,已被证明可以改善聚合物及其复合材料的力学性能。然而,研究者们开发的多种实验途径并不能使CNTs自身的作用在碳纤维复合材料增强过程中完全发挥出来。为了从本质上了解CNTs对复合材料性能的影响,需要辅之以合适的模型方法。
本文基于目前的研究成果提出需从纳米-介观尺度出发,采用合适的方法(分子动力学方法(MD)、有限元法(FE)、解析法)分析CNTs对碳纤维复合材料力学性能的影响。这三类方法适用于不同的尺度和情况之下,需要研究者根据需要采用单一方法或者多种方法相辅相成的途径分析影响机制。
目前,已经有大量可靠的模拟结果可证明CNTs对复合材料具有增强作用,但依然存在如下问题:
(1) 实验方法得到的结果与模拟结果之间有明显的差距,说明模拟过程中所用的输入参数并没有充分考虑到CNTs在基体当中的真实状态。
(2) 受计算能力和计算成本的限制,模拟过程无法完美呈现研究者希望达到的CNTs存在状态,直接影响计算结果的可信度。
(3) 研究者们处理CNTs增强复合材料计算问题的方法不尽相同,尚未形成一套公认的、可适用于多种情况的处理方法。
(4) 模拟过程中,由于研究思路和出发角度的不同,同一研究变量对纳米复合材料力学性能的影响规律存在差异,但CNTs可作为复合材料增强体的结论依然成立。
| [1] |
PAL G, KUMAR S. Modeling of carbon nanotubes and carbon nanotube-polymer composites[J]. Progress in Aerospace Sciences, 2016, 80: 33-58. DOI:10.1016/j.paerosci.2015.12.001 |
| [2] |
MA P C, SIDDIQUI N A, MAROM G, et al. Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites:a review[J]. Composites:Part A, 2010, 41(10): 1345-1367. DOI:10.1016/j.compositesa.2010.07.003 |
| [3] |
GOJNY F H, WICHMANN M H G, KOPKE U. Carbon nanotube-reinforced epoxy-composites: enhanced stiffness and fracture toughness at low nanotube content[J]. Composites Science & Technology, 2004, 64(15): 2363-2371. |
| [4] |
BEKYAROVA E, THOSTENSON E T, YU A, et al. Multiscale carbon nanotube?carbon fiber reinforcement for advanced epoxy composites[J]. Langmuir: the ACS Journal of Surfaces and Colloids, 2007, 23(7): 3970-3974. DOI:10.1021/la062743p |
| [5] |
WICKS S S, DE VILLORIA R G, WARDLE B L. Interlaminar and intralaminar reinforcement of composite laminates with aligned carbon nanotubes[J]. Composites Science and Technology, 2010, 70: 20-28. DOI:10.1016/j.compscitech.2009.09.001 |
| [6] |
HE X, ZHANG F, WANG R, et al. Preparation of a carbon nanotube/carbon fiber multi-scale reinforcement by grafting multi-walled carbon nanotubes onto the fibers[J]. Carbon, 2007, 45(13): 2559-2563. DOI:10.1016/j.carbon.2007.08.018 |
| [7] |
GARCIA E J, WARDLE B L, HART A J. Joining prepreg composite interfaces with aligned carbon nanotubes[J]. Composites:Part A, 2008, 39(6): 1065-1070. DOI:10.1016/j.compositesa.2008.03.011 |
| [8] |
KHAN S U, KIM J K. Improved interlaminar shear properties of multiscale carbon fiber composites with bucky paper interleaves made from carbon nanofibers[J]. Carbon, 2012, 50(14): 5265-5277. DOI:10.1016/j.carbon.2012.07.011 |
| [9] |
SHIM B S, ZHU J, JAN E, et al. Multiparameter structural optimization of single-walled carbon nanotube composites: toward record strength, stiffness, and toughness[J]. ACS Nano, 2009, 3(7): 1711-1722. DOI:10.1021/nn9002743 |
| [10] |
GOJNY F H, WICHMANN M H G, FIEDLER B, et al. Evaluation and identification of electrical and thermal conduction mechanisms in carbon nanotube/epoxy composites[J]. Polymer, 2006, 47(6): 2036-2045. DOI:10.1016/j.polymer.2006.01.029 |
| [11] |
GOJNY F H, WICHMANN M H G, FIEDLER B, et al. Influence of different carbon nanotubes on the mechanical properties of epoxy matrix composites-a comparative study[J]. Composites Science & Technology, 2005, 65(15/16): 2300-2313. |
| [12] |
PARK J J, PARK D M, YOUK J H, et al. Functionalization of multi-walled carbon nanotubes by free radical graft polymerization initiated from photoinduced surface groups[J]. Carbon, 2010, 48(10): 2899-2905. DOI:10.1016/j.carbon.2010.04.024 |
| [13] |
MORADIDASTJERDI R, PAYGANEH G, TAJDARI M. The effects of carbon nanotube orientation and aggregation on static behavior of functionally graded nanocomposite cylinders[J]. Journal of Solid Mechanics, 2017, 9(1): 198-212. |
| [14] |
LIU Q, LOMOV S V, GORBATIKH L. The interplay between multiple toughening mechanisms in nanocomposites with spatially distributed and oriented carbon nanotubes as revealed by dual-scale simulations[J]. Carbon, 2018, 142: 141-149. |
| [15] |
WAGNER H D, AJAYAN P M, SCHULTE K. Nanocomposite toughness from a pull-out mechanism[J]. Composites Science & Technology, 2013, 83: 27-31. |
| [16] |
NADIV R, SHACHAR G, PERETZ-DAMARI S, et al. Performance of nano-carbon loaded polymer composites: dimensionality matters[J]. Carbon, 2018, 126: 410-418. DOI:10.1016/j.carbon.2017.10.039 |
| [17] |
NEEDLEMAN A, BORDERS T L, BRINSON L C, et al. Effect of an interphase region on debonding of a CNT reinforced polymer composite[J]. Composites Science & Technology, 2010, 70(15): 2207-2215. |
| [18] |
ROMANOV V S, LOMOV S V, VERPOEST I, et al. Modelling evidence of stress concentration mitigation at the micro-scale in polymer composites by the addition of carbon nanotubes[J]. Carbon, 2015, 82: 184-194. DOI:10.1016/j.carbon.2014.10.061 |
| [19] |
GREEF N D, GORBATIKH L, LOMOV S V, et al. Damage development in woven carbon fiber/epoxy composites modified with carbon nanotubes under tension in the bias direction[J]. Composites: Part A, 2011, 42(11): 1635-1644. DOI:10.1016/j.compositesa.2011.07.013 |
| [20] |
ZHOU H, DU X, LIU H Y, et al. Delamination toughening of carbon fiber/epoxy laminates by hierarchical carbon nanotube-short carbon fiber interleaves[J]. Composites Science & Technology, 2017, 140: 46-53. |
| [21] |
LIU Y, WILKINSON A. Rheological percolation behaviour and fracture properties of nanocomposites of MWCNTs and a highly crosslinked aerospace-grade epoxy resin system[J]. Composites:Part A, 2018, 105: 97-107. DOI:10.1016/j.compositesa.2017.11.012 |
| [22] |
ESKIZEYBEK V, YAR A, AVC A. CNT-PAN hybrid nanofibrous mat interleaved carbon/epoxy laminates with improved mode Ⅰ interlaminar fracture toughness[J]. Composites Science & Technology, 2018, 157: 30-39. |
| [23] |
QUARESIMIN M, SALVIATO M, ZAPPALORTO M. Strategies for the assessment of nanocomposite mechanical properties[J]. Composites:Part B, 2012, 43(5): 2290-2297. DOI:10.1016/j.compositesb.2011.12.012 |
| [24] |
LI Y L, WANG S J, WANG Q, et al. Enhancement of fracture properties of polymer composites reinforced by carbon nanotubes:a molecular dynamics study[J]. Carbon, 2018, 129: 504-509. DOI:10.1016/j.carbon.2017.12.029 |
| [25] |
ZHANG J, JIANG D, SCARPA F, et al. Enhancement of pullout energy in a single-walled carbon nanotube-polyethylene composite system via auxetic effect[J]. Composites:Part A, 2013, 55: 188-194. DOI:10.1016/j.compositesa.2013.09.006 |
| [26] |
ALIAN A R, MEGUID S A. Molecular dynamics simulations of the effect of waviness and agglomeration of CNTs on interface strength of thermoset nanocomposites[J]. Physical Chemistry Chemical Physics, 2017, 19(6): 4426-4434. DOI:10.1039/C6CP07464B |
| [27] |
FRANKLAND S J V, HARIK V M, ODEGARD G M, et al. The stress-strain behavior of polymer-nanotube composites from molecular dynamics simulation[J]. Composites Science & Technology, 2003, 63(11): 1655-1661. |
| [28] |
RUIZ L, XIA W, MENG Z, et al. A coarse-grained model for the mechanical behavior of multi-layer graphene[J]. Carbon, 2015, 82: 103-115. DOI:10.1016/j.carbon.2014.10.040 |
| [29] |
ZHAO J, JIANG J W, WANG L, et al. Coarse-grained potentials of single-walled carbon nanotubes[J]. Journal of the Mechanics & Physics of Solids, 2014, 71: 197-218. |
| [30] |
ARASH B. Coarse-grained model of the J-integral of carbon nanotube reinforced polymer composites[J]. Carbon, 2015, 96(5): 1084-1092. |
| [31] |
DUAN K, LI L, WANG F, et al. Importance of interface in the coarse-grained model of CNT/epoxy nanocomposites[J]. Nanomaterials, 2019, 9(10): 1479. DOI:10.3390/nano9101479 |
| [32] |
ODEGARD G M, GATES T S, WISE K E, et al. Constitutive modeling of nanotube-reinforced polymer composites[J]. Composites Science & Technology, 2003, 63(11): 1671-1687. |
| [33] |
JIA Y Y, CHEN Z R, YAN W Y. A numerical study on carbon nanotube pullout to understand its bridging effect in carbon nanotube reinforced composites[J]. Composites: Part B, 2015, 81: 64-71. DOI:10.1016/j.compositesb.2015.07.003 |
| [34] |
KULKARNI M, CARNAHAN D, KULKARNI K, et al. Elastic response of a carbon nanotube fiber reinforced polymeric composite:a numerical and experimental study[J]. Composites:Part A, 2010, 41(5): 414-421. DOI:10.1016/j.compositesb.2009.09.003 |
| [35] |
COOPER C A, COHEN S R, BARBER A H, et al. Detachment of nanotubes from a polymer matrix[J]. Applied Physics Letters, 2002, 81(20): 3873-3875. DOI:10.1063/1.1521585 |
| [36] |
ROMANOV V S, LOMOV S V, VERPOEST I, et al. Can carbon nanotubes grown on fibers fundamentally change stress distribution in a composite?[J]. Composites: Part A, 2014, 63: 32-34. DOI:10.1016/j.compositesa.2014.03.021 |
| [37] |
ROMANOV V, LOMOV S V, VERPOEST I, et al. Inter-fiber stresses in composites with carbon nanotube grafted and coated fibers[J]. Composites Science and Technology, 2015, 114: 79-86. DOI:10.1016/j.compscitech.2015.04.013 |
| [38] |
RAI A, CHATTOPADHYAY A. Multifidelity multiscale modeling of nanocomposites for microstructure and macroscale analysis[J]. Composite Structures, 2018, 200: 204-216. DOI:10.1016/j.compstruct.2018.05.075 |
| [39] |
LIU Q, LOMOV S V, GORBATIKH L. When does nanotube grafting on fibers benefit the strength and toughness of composites?[J]. Composites Science & Technology, 2020, 188: 107989. |
| [40] |
LIU Q, GORBATIKH L, LOMOV S V. A combined use of embedded and cohesive elements to model damage development in fibrous composites[J]. Composite Structures, 2019, 223: 1-14. |
| [41] |
LU F Z, LIU Q, DRUZHININ P, et al. Reduction of the volume redundancy in combined embedded elements/cohesive zone modelling-Comments on the paper: Liu Q, Gorbatikh L, Lomov SV[J]. A combined use of embedded and cohesive elements to model damage development in fibrous composites, Composite Structures, 2019, 223: 110921. |
| [42] |
RAI A, SUBRAMANIAN N, CHATTOPADHYAY A. Investigation of damage mechanisms in CNT nanocomposites using multiscale analysis[J]. International Journal of Solids & Structures, 2017, 120: 115-124. |
| [43] |
LIU H, ZENG D, LI Y, et al. Development of RVE-embedded solid elements model for predicting effective elastic constants of discontinuous fiber reinforced composites[J]. Mechanics of Materials, 2016, 93: 109-123. DOI:10.1016/j.mechmat.2015.10.011 |
| [44] |
TABATABAEI S A, LOMOV S V, VERPOEST I. Assessment of embedded element technique in meso-FE modelling of fibre reinforced composites[J]. Composite Structures, 2014, 107: 436-446. DOI:10.1016/j.compstruct.2013.08.020 |
| [45] |
LIU Q, LOMOV S V, LARISSA G. Spatial distribution and orientation of nanotubes for suppression of stress concentrations optimized using genetic algorithm and finite element analysis[J]. Materials & Design, 2018, 158: 136-146. |
| [46] |
BLANCO J, GARCIA E J, GUZMAN D V R, et al. Limiting mechanisms of mode I interlaminar toughening of composites reinforced with aligned carbon nanotubes[J]. Journal of Composite Materials, 2009, 43(8): 825-841. DOI:10.1177/0021998309102398 |
| [47] |
LIU B, CHEN Y L. Failure analysis and the optimal toughness design of carbon nanotube-reinforced composites[J]. Composites Science & Technology, 2010, 70: 1360-1367. |
| [48] |
MENNA C, BAKIS C E, PROTA A. Effect of nanofiller length and orientation distributions on mode Ⅰ fracture toughness of unidirectional fiber composites[J]. Journal of Composite Materials, 2015, 50: 1331-1352. |
| [49] |
THOSTENSON E T, CHOU T W. On the elastic properties of carbon nanotube-based composites: modelling and characterization[J]. Journal of Physics D, 2003, 36(5): 573-582. DOI:10.1088/0022-3727/36/5/323 |
| [50] |
ZHU F, PARK C, YUN G J. An extended Mori-Tanaka micromechanics model for wavy CNT nanocomposites with interface damage[J]. Mechanics of Advanced Materials & Structures. DOI:10.1080/15376494.2018.1562135 |
| [51] |
FERRARI M, JOHNSON G C. Effective elasticities of short-fiber composites with arbitrary orientation distribution[J]. Mechanics of Materials, 1989, 8(1): 67-73. DOI:10.1016/0167-6636(89)90006-9 |
| [52] |
HESHMATI M, YAS M H. Free vibration analysis of functionally graded CNT-reinforced nanocomposite beam using Eshelby-Mori-Tanaka approach[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3403-3408. DOI:10.1007/s12206-013-0862-8 |
| [53] |
CHEN Y L, LIU B, HUANG Y, et al. Fracture toughness of carbon nanotube-reinforced metal- and ceramic-matrix composites[J]. Journal of Nanomaterials, 2011, 2011(6584): 74609. |
| [54] |
ZHANG R F, NING Z Y, XU Z W, et al. Interwall friction and sliding behavior of centimeters long double-walled carbon nanotubes[J]. Nano Letters, 2016, 16(16): 1367-1374. |
| [55] |
DAVOUDABADI M R, FARAHANI S D. Investigation of vacancy defects on the Young's modulus of carbon nanotube reinforced composites in axial direction via a multiscale modeling approach[J]. Journal of Solid Mechanics, 2010, 2(3): 248-256. |
| [56] |
PALACIOS J A, GANESAN R. Reliability evaluation of carbon-nanotube-reinforced-polymer composites based on multiscale finite element model[J]. Composite Structures, 2019, 229: 111381. DOI:10.1016/j.compstruct.2019.111381 |
| [57] |
SHARMA S, CHANDRA R, KUMAR P, et al. Effect of Stone-Wales and vacancy defects on elastic moduli of carbon nanotubes and their composites using molecular dynamics simulation[J]. Computational Materials Science, 2014, 86: 1-8. DOI:10.1016/j.commatsci.2014.01.035 |
| [58] |
JIANG C, ZHANG J, LIN S, et al. Effects of free organic groups in carbon nanotubes on glass transition temperature of epoxy matrix composites[J]. Composites Science & Technology, 2015, 118: 269-275. |
| [59] |
BRIGHT I, KOUTSOS V, LI Q, et al. Carbon nanotubes for integration into nanocomposite materials[J]. Microelectronic Engineering, 2006, 83(4/9): 1542-1546. |
| [60] |
MA P C, MO S Y, TANG B Z, et al. Dispersion, interfacial interaction and re-agglomeration of functionalized carbon nanotubes in epoxy composites[J]. Carbon, 2010, 48(6): 1824-1834. DOI:10.1016/j.carbon.2010.01.028 |
| [61] |
ZIAEI H, FAGHIDIAN S A, OMIDI M J. Agglomeration effects of carbon nanotube on residual stresses in polymer nano composite using experimental and analytical method[J]. Materials Research Express, 2018, 6(3): 035009. DOI:10.1088/2053-1591/aaf370 |
| [62] |
ROMANOV V S, LOMOV S V, VERPOEST I, et al. Stress magnification due to carbon nanotube agglomeration in composites[J]. Composite Structures, 2015, 133: 246-256. DOI:10.1016/j.compstruct.2015.07.069 |
| [63] |
ALIAN A R, KUNDALWAL S I, MEGUID S A. Multiscale modeling of carbon nanotube epoxy composites[J]. Polymer, 2015, 70: 149-160. DOI:10.1016/j.polymer.2015.06.004 |
| [64] |
PAN J, BIAN L, ZHAO H, et al. A new micromechanics model and effective elastic modulus of nanotube reinforced composites[J]. Computational Materials Science, 2016, 113: 21-26. DOI:10.1016/j.commatsci.2015.11.009 |
| [65] |
CHANTELI A, TSERPES K I. Finite element modeling of carbon nanotube agglomerates in polymers[J]. Composite Structures, 2015, 132: 1141-1148. DOI:10.1016/j.compstruct.2015.07.033 |
| [66] |
MATVEEVA A Y, LOMOV S V, GORBATIKH L. Debonding at the fiber/matrix interface in carbon nanotube reinforced composites: modelling investigation[J]. Computational Materials Science, 2019, 159: 412-419. DOI:10.1016/j.commatsci.2018.10.031 |
| [67] |
NAZARENKO L, CHIRKOV A Y, STOLARSKI H, et al. On modeling of carbon nanotubes reinforced materials and on influence of carbon nanotubes spatial distribution on mechanical behavior of structural elements[J]. International Journal of Engineering Science, 2019, 143: 1-13. DOI:10.1016/j.ijengsci.2019.06.008 |
 2020, Vol. 48
2020, Vol. 48