2. 武汉大学海洋研究院, 湖北 武汉 430079
2. Institute of Marine Science and Technology, Wuhan University, Wuhan 430079, China
海底控制网是海洋大地测量的重要研究内容,是海底板块运动监测、海洋工程定位的参考基准[1]。目前,海底网点坐标主要采用海面运动平台圆走航方式,通过测距交会实现基准的绝对传递,进一步通过海底网点间相互测距,实施网平差来确定,海洋环境场是影响其精度的首要因素。为提高点位精度,在海底控制网测量和解算方面,国内外学者开展了广泛研究,主要聚焦在声速获取、声速误差对测距影响、深度约束和声学差分定位等方面。本文将对这些研究内容进行剖析,明确其特点和适用性,为海底网点高精度测量和解算服务。
1 海洋声速及获取海底网点坐标常通过距离交会确定,距离是基本观测量,但精确距离需利用声波在海水中传播的时间和声速,借助声线跟踪技术得到[2]。若采用的换能器、应答器工作正常,声线在海水中历时准确,则声速成为影响测距的首要因素。声速可借助海水温度、盐度和密度/深度来表示,其中温度是第一影响要素,其次是盐度和深度。典型海区,海水表层和温跃层声速变化大,等温层变化小。声速还受局部流场影响。涡流、紊流等交换了不同深度海水,导致温度场紊乱,影响声速场。一天内气温变化会影响表层温度,但对深层影响较小;季节性温度、流场变化会给声速剖面(SVP)整体产生影响。综上,整个海洋声速场存在明显时空变化和局部不规律变化。图 1给出了圣地亚哥诺马角和吕宋海峡2个水域48 h的定点、等时间间隔SVP时序[3],前者变化超过10 m/s,后者达40 m/s,且无规律。这种现象在其他海域同样存在,因此无法基于声速所谓的时变规律来消除或削弱声速影响。
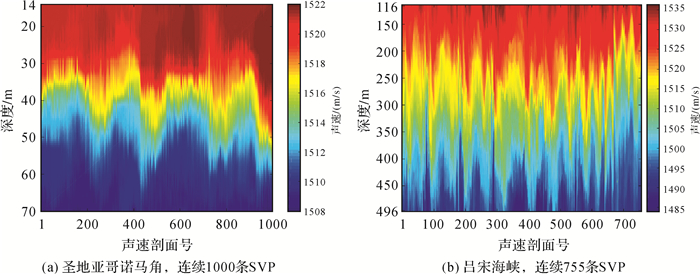
|
| 图 1 声速剖面变化 Fig. 1 Sound velocity variation with time |
为获取高精度几何距离和实现海底点高精度定位,在测量水域沿声线传播路径按一定时间和空间开展SBP测量非常必要,但同时也降低了作业效率。为提高声速获取效率和精度,近年先后出现了SVP反演法、基于声速规律时变的SVP内插法、基于有限SVP的声速场构建法[4-9]。反演法解决了无SVP时声速获取问题,但得到的是一个等效SVP,据此无法通过声线跟踪得到声波真实传播路线,且反演的SVP精度低,不建议采用。图 1已表明海洋声速具有时变特点,但规律性不强,因此基于声速规律时变假设、利用前后段SVP内插当前SVP在机理上不成立,必将带来较大内插误差。定点测量的SVP难以满足声线跟踪对声波传播路径中不同位置、深度声速的要求,由此带来的误差称为声速代表性误差。基于有限SVP构建声速场可很好地解决这一问题,但需解决SVP站间变化规律问题,是目前研究的一个难点。声速空间场建设和维护也是海底网建成后开展高精度导航定位必不可少的工作。
2 声速对测距的影响获得了声波传播路径上不同深度的声速后,借助层内常梯度/常声速声线跟踪法可获得声线及换能器到应答器间几何距离[10]。为简化,下面采用常声速声线跟踪方法开展声速对测距影响分析。将声线经历的整个水体划分为N层,第i层厚度为zi,声速为Ci,其上层入射角和声速分别为θi-1和Ci-1,根据Snell法则
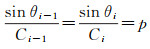 (1)
(1)
声波第i层传播时间ti和水平距离yi为
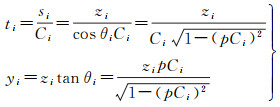 (2)
(2)
则声线总的传播时间T和水平距离Y为
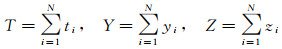 (3)
(3)
换能器至应答器间直线距离为
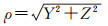 (4)
(4)
由以上可知,SVP总存在误差,也必将给ρ带来影响。若仅顾及初始入射角θ0误差影响,对式(1)两边微分可得dθ0对Snell常数p影响的表达式;对式(2)关于p偏微分可得dθ0对ti和yi影响。若zi由高精度压力传感器提供,则dθ0对ρ影响为
 (5)
(5)
式中,θ0和C0分别为初始入射角和表层声速。
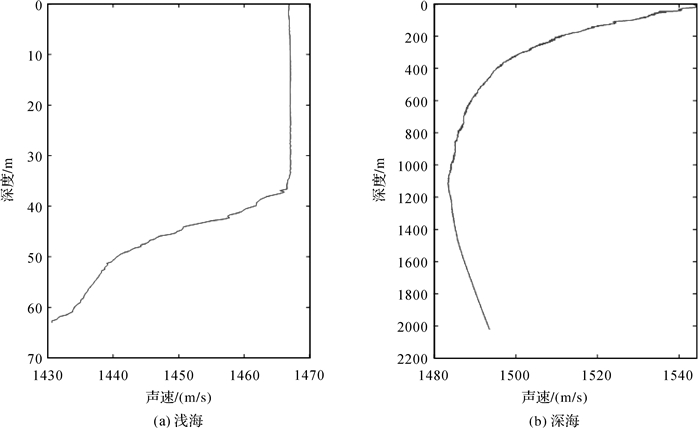
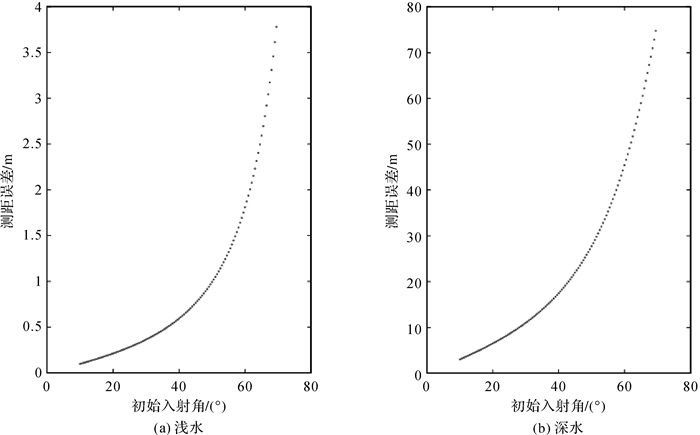
式(5)表明,dθ0对ρ影响与入射角和深度具有非线性关系。利用水深60 m、2000 m实测SVP和声学测距数据开展试验(图 2),给不同初始入射角附加0.5°误差,由此产生的ρ误差如图 3所示。
|
| 图 2 浅海(a)和深海(b)声速剖面 Fig. 2 Sound velocity profile in shallow water (a) and deep water (b) |
|
| 图 3 浅水(a)和深水(b)情况下初始入射角误差引起的测距误差 Fig. 3 Ranging error due to initial incident angle error in shallow water (a) and deep water (b) |
可以看出,dθ0对ρ的影响非线性,且随θ0和深度增大快速增大。由式(1)和式(2)可知,声速误差会影响声线折射角和距离计算。为简化,仅顾及表层声速误差,下面分析声速误差dC0对ρ的影响。对式(1)关于声速求导,获得层内声速误差dCi对层入射角影响dθi
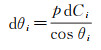
将式(6)代入式(5)中,可得表层声速误差对测距的影响为
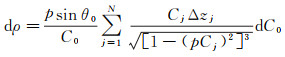
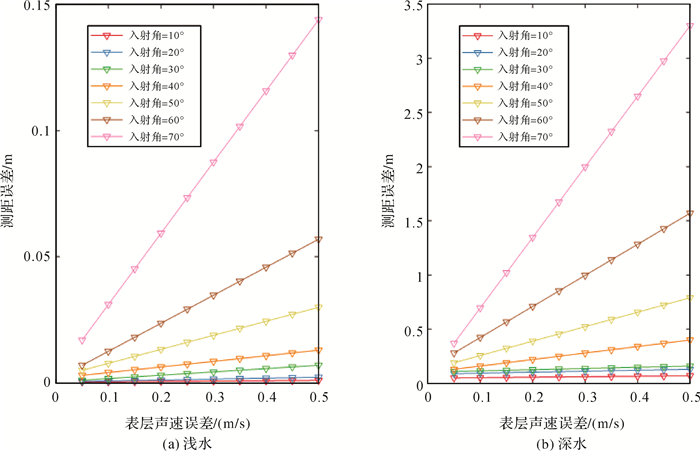
采用图 2中数据,为表层声速附加0~0.5 m/s不同声速误差,由式(7)计算得到的dρ随深度、入射角的变化如图 4所示。可以看出:①入射角相同时,dρ随dC增大而增大;②dC相同时,dρ随波束入射角的增大而增大;③浅水区,即使在大入射角情况下,测距误差依然很小;在深水区,入射角较大时,微小的声速误差会带来显著的测距误差。
|
| 图 4 浅水(a)和深水(b)情况下表层声速误差引起的测距误差 Fig. 4 Ranging error due to surface sound speed error in shallow water (a) and deep water (b) |
以上仅顾及表层声速误差,实则每层声速均存在误差,综合影响下dρ模型会更复杂,再叠加入射角误差影响,dρ随入射角、深度的变化将呈现非线性。因此,在削弱声速误差影响时应同时顾及声速、入射角和深度。
3 深度及深度差约束海底网解算中,受空间网形结构影响,控制点的垂线解z精度不高甚至出现解算不稳定问题[11-12]。为此,海底网测量时,利用压力传感器也开展深度/深度差测量,并将高精度测量值引入海底网数据解算中。许多学者以深度/深度差为约束,将换能器到应答器间空间直线转换为平面直线,借助平面距离交会确定待求点坐标;或将该深度作为高精度观测量,与空间距离方程组联合解算待求点坐标[13-14]。以上方法均确保了控制点z精度,也改善了点位精度。
压力传感器根据水面到压力传感器中心压力差变化获取精度为0.1%~0.3%的深度[14]。若两点所在海域潮高一致,则由压力传感器提供的深度和由此计算的点间深度差相对声学测距具有较高的精度,可以帮助提高测距精度和改善最终点位精度。但当点间距离较远时,如海底网点间距离为几千米到二十几千米,此时两点的海面潮高会存在较大差异,直接利用深度/深度差会给最终计算结果带来较大误差,为此必须考虑潮高差影响。潮高差消除需根据海底网测量中圆走航基准传递、海底网测量两项内容区别对待。
(1) 圆走航基准传递。大量文献已证明,圆走航半径等于水深时定位精度最高[11, 15]。浅水时圆走航半径较小,可认为船载换能器、海底应答器两处水域潮高近似。深水时圆走航半径较大,但深水区潮位变化较小,也可认为两处的潮位近似相同。
(2) 海底网测量。海底网点间距离较大,在近海各点所在水域会存在较大潮高差。各点的潮位变化可根据各自压力传感器提供的水深序列来获得,但因所得潮位均参考各自零点,需在各自位置与GNSS潮位进行短时比较或根据两站的潮位序列借助综合传递法,消除两点间零点差来获取两点间潮高差。在远海,两海底网点间的潮位变化会较小,加之定位误差会因为水深增加而降低,潮高差问题可以不予考虑。
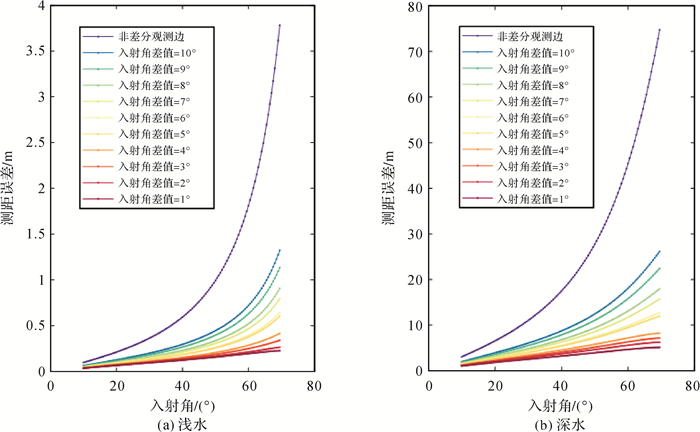
4 声学差分定位为解决无SVP时的定位问题,国内外一些学者提出了声学差分定位方法,即借助GNSS局域差分定位思想,认为局域声速稳定,声速对测距影响近似,通过对距离差分消除或削弱声速影响,并借助距离差解算点位坐标[16-18]。由声线跟踪理论可知,不同GNSS测距,声速误差带来的测距影响显著且具有累积性。声速对测距影响还与波束入射角、深度相关。目前一些研究仅顾及了声速误差,忽视了后两个因素,因此在机理上存在缺陷,且会导致定位精度较低。为验证这一结论,从图 2走航测量数据中分别抽取入射角小于设定角间隔的声线并求差,联合距离差、各距离观测时刻的GNSS三维解,确定海底点坐标。以传统声线跟踪、交会定位确定的海底点坐标结果为参考,评估差分定位精度。由图 5可以看出:
|
| 图 5 浅水(a)和深水(b)情况下差分观测边误差 Fig. 5 Differential observation range error in shallow water (a) and deep water (b) |
(1) 差分定位提高了未顾及声速情况下(图 3中初始测距误差)的定位精度;
(2) 随着水深、入射角和角度间隔越大,差分定位的精度越来越低;
(3) 若设定定位限差为10 cm,水深60 m、入射角70°时差分定位满足精度要求。但若水深达到2000 m,入射角70°时入射角度差小于1°、2°时的定位结果才能满足要求。
以上表明,差分定位时用入射角相同或相近的测量距离开展差分定位是必要的。
5 结论综上得出如下结论:①声速场变化显著且无规律,不能据此消除声速误差影响;②声速场构建是削弱声速代表性误差的有效途径;③削弱声速误差对测距定位影响应同时顾及声速、波束入射角和深度;④差分定位应利用入射角近似相同的距离开展差分计算;⑤开展深度/深度差约束定位时,在近海应顾及两点间的潮高差。
| [1] | WATANABE S I, ISHIKAWA T, YOKOTA Y. Non-volcanic crustal movements of the northernmost Philippine Sea plate detected by the GPS-acoustic seafloor positioning[J]. Earth, Planets and Space, 2015(67): 184. |
| [2] |
兰华林, 孙大军, 张殿伦, 等.
海底应答器绝对位置快速校准[J]. 计算机工程与应用, 2007, 43(22): 191–193.
LAN Hualin, SUN Dajun, ZHANG Dianlun, et al. Rapid calibration of absolute position of transponder on seabed[J]. Computer Engineering and Applications, 2007, 43(22): 191–193. DOI:10.3321/j.issn:1002-8331.2007.22.057 |
| [3] | BIANCO M, GERSTOFT P. Dictionary learning of sound speed profiles[J]. The Journal of the Acoustical Society of America, 2017, 141(3): 1749–1758. DOI:10.1121/1.4977926 |
| [4] |
张忠兵, 马远良, 倪晋平, 等.
基于声线到达时差的浅海声速剖面反演[J]. 西北工业大学学报, 2002, 20(1): 36–39.
ZHANG Zhongbing, MA Yuanliang, NI Jinping, et al. A new and practical method for inverting sound speed profile in shallow water[J]. Journal of Northwestern Polytechnical University, 2002, 20(1): 36–39. DOI:10.3969/j.issn.1000-2758.2002.01.009 |
| [5] |
张维, 杨士莪, 黄益旺, 等.
基于爆炸声传播时间的声速剖面反演[J]. 振动与冲击, 2012, 31(23): 6–11.
ZHANG Wei, YANG Shi'e, HUANG Yiwang, et al. Inversion of sound speed profile based on explosive sound transmission time[J]. Journal of Vibration and Shock, 2012, 31(23): 6–11. DOI:10.3969/j.issn.1000-3835.2012.23.002 |
| [6] |
胡合欢, 崔永胜, 周进忠, 等.
BP神经网络在构建声速场中的应用研究[J]. 海洋测绘, 2015, 35(5): 67–70.
HU Hehuan, CUI Yongsheng, ZHOU Jinzhong, et al. Application of back-propagation neural network in establishing velocity fields[J]. Hydrographic Surveying and Charting, 2015, 35(5): 67–70. DOI:10.3969/j.issn.1671-3044.2015.05.017 |
| [7] |
李洪超, 文汉江, 蔡艳辉, 等.
基于Argo浮标和EOF建立区域海水三维声速场的方法[J]. 测绘科学, 2012, 37(2): 74–76.
LI Hongchao, WEN Hanjiang, CAI Yanhui, et al. Modeling three-dimensional acoustic field in the ocean by using Argo and EOF[J]. Science of Surveying and Mapping, 2012, 37(2): 74–76. |
| [8] |
吴永亭. LBL精密定位理论方法研究及软件系统研制[D].武汉: 武汉大学, 2013. WU Yongting. Study on theory and method of precise LBL positioning and development of positioning software system[D]. Wuhan: Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135465.htm |
| [9] |
赵建虎.
现代海洋测绘[M]. 武汉: 武汉大学出版社, 2008.
ZHAO Jianhu. Modern marine surveying and charting[M]. Wuhan: Wuhan University Press, 2008. |
| [10] | ZHAO Jianhu, CHEN Xinhua, ZHANG Hongmei, et al. Localization of an underwater control network based on quasi-stable adjustment[J]. Sensors, 2018, 18(4): 950. DOI:10.3390/s18040950 |
| [11] | ZHAO Jianhu, ZOU Yajing, ZHANG Hongmei, et al. A new method for absolute datum transfer in seafloor control network measurement[J]. Journal of Marine Science and Technology, 2016, 21(2): 216–226. DOI:10.1007/s00773-015-0344-z |
| [12] |
赵建虎, 陈鑫华, 吴永亭, 等.
顾及波浪影响和深度约束的水下控制网点绝对坐标的精确确定[J]. 测绘学报, 2018, 47(3): 413–421.
ZHAO Jianhu, CHEN Xinhua, WU Yongting, et al. Determination of absolute coordinate of underwater control point taking waves and depth's constraint into account[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 413–421. DOI:10.11947/j.AGCS.2018.20170246 |
| [13] |
赵建虎, 邹亚靖, 吴永亭, 等.
深度约束的海底控制网点坐标确定方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 137–141.
ZHAO Jianhu, ZOU Yajing, WU Yongting, et al. Determination of underwater control point coordinate based on constraint of water depth[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 137–141. DOI:10.11918/j.issn.0367-6234.2016.10.020 |
| [14] |
任国晶.深度传感器的研制与实验[D].哈尔滨: 哈尔滨工业大学, 2012. REN Guojing. Research and experiment of the depth sensor[D]. Harbin: Harbin Institute of Technology, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2237096 |
| [15] | CHEN H H, WANG C C. Optimal localization of a seafloor transponder in shallow water using acoustic ranging and GPS observations[J]. Ocean Engineering, 2007, 34(17-18): 2385–2399. DOI:10.1016/j.oceaneng.2007.05.005 |
| [16] | XU Peiliang, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795–808. DOI:10.1186/BF03351859 |
| [17] |
王权, 程鹏飞, 章传银, 等.
差分GPS水下立体定位系统[J]. 测绘科学, 2006, 31(5): 18–19, 21.
WANG Quan, CHENG Pengfei, ZHANG Chuanyin, et al. Underwater positioning system Based on DGPS[J]. Science of Surveying and Mapping, 2006, 31(5): 18–19, 21. DOI:10.3771/j.issn.1009-2307.2006.05.003 |
| [18] |
蔡艳辉.差分GPS水下定位系统集成关键技术研究[D].阜新: 辽宁工程技术大学, 2007. CAI Yanhui. Investigations on integration of underwater GPS positioning system[D]. Fuxin: Liaoning Technical University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10147-2008050896.htm |



