2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 武汉大学测绘学院, 湖北 武汉 430079
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
海底大地控制网是建立海洋大地测量基准的重要手段,对我国海洋强国的战略具有重要保障作用,无论是海洋测绘工作还是海洋科学研究活动,都需要其作为基础保障设施。目前确定海底控制点三维绝对坐标的技术手段主要采用GNSS结合声学定位[1-7]。GNSS可以提供测量船高精度的三维坐标[8],声学设备可以获取测量船底换能器到海底应答器的斜距值[9],经过多次测量,利用距离交汇的方法即可解算出海底控制点的三维绝对坐标[10]。影响该方法定位精度最主要的因素是声速的不确定性所引起的测距误差[11-12]。
针对上述问题,国内外的学者提出了不同的解决办法。文献[13]将3~4个应答器在海底均匀地布设在一个圆上,将圆心作为虚拟的控制点,由于海水声速垂直分层的性质,这样做的好处可以提高虚拟控制点水平坐标解的精度,但垂直解的精度仍然较差。文献[14]将差分的思想引入控制点坐标的解算,对连续两个历元的观测方程进行差分,这种方法可以有效消除声速长周期项的影响,但短周期项依旧存在。还有一类的做法是对声速测距误差进行参数化建模,将模型的未知参数与坐标改正值一并作为待估参数进行解算[15-16],因为海水声速的变化主要发生在上层,海底处于恒温层,声速稳定,因此应答器的互测距值精度较高。文献[17]将这一性质引入到应答器坐标的测定,不但提高了应答器间相对位置的精度,同时还提高了作业的效率,但这种方法无法改进控制点绝对坐标的准确性。文献[18]对此方法进行了改进,首先利用圆走航的方法获得部分控制点的绝对坐标后,再开展应答器间的互测距,最后利用网平差的方法解算所有控制点的三维坐标[18-19],实测试验证明了这种方法可以将控制点坐标的解算精度提高一个数量级,但其自身依然存在一定的局限性,因为声线弯曲,海底地形会阻隔声波的传递,因此应答器互测距的距离有限,通常仅几百米[20-21],这很难满足深海条件下的实际需要。此外,控制点的水深值通常是由压力传感器测量的压力值转化而来,转化模型的误差会随着深度的增加指数型上涨[22-23],在深海条件下该值的准确性和可靠性将大大降低,因此目前传统方法均无法获得深海条件下控制点垂直方向准确的绝对坐标值。
通过上述的分析得知,目前确定深海海底控制点绝对坐标的问题在于垂直解的准确度低,而产生这一问题的主要原因是声速的不确定性。为改善控制点垂直解的准确性,本文首先研究了声速剖面在时间上的变化规律,并分析了声速剖面的不确定性对水下声学测距误差的影响。然后研究测量船最佳的走航路径,并提出了附加水平距离和深度差约束的控制点水下差分解算模型。最后,通过仿真试验对该方法的有效性进行了验证。
1 声速剖面的不确定性对测距误差的影响声速剖面可认为由两部分组成,包括不随时间变化的背景声速剖面和随时间变化的瞬时变化部分。由内波、潮汐、温度日变化引起声速剖面的变化具有明显周期性的特征。太阳辐射引起表层海水温度的周期性变化,表层海水热量通过热传导影响上层一定深度下温度的变化,由温度变化导致海水声速剖面产生周期性变化。内波会引起海水垂向运动,从而使上下层海水产生热量交换,同样使得某一厚度水层内声速剖面发生周期性变化,但相比于温度日变化,周期较短。潮汐的作用会产生潮内波或半潮日内波,它属于内波的一种,因此对声速剖面影响的机理与内波相同,但周期与潮汐相同,属于声速剖面变化的长周期项。声速剖面周期性的变化使得声速剖面面积也呈相同的变化规律,其中温度日变化和潮汐所引起的变化为长周期项,由内波引起的为短周期项。
声速剖面的不确定性是影响水下声学测距精度最主要的因素,它所引起的测距误差可分为两部分,一部分是由背景声速剖面测量的不准确引起,另一部分是由海洋内波、潮汐、温度日变化所引起的周期性误差[24]。内波引起的测距误差为短周期项,而潮汐和温度日变化引起的测距误差为长周期项,这些规律由实际测量经验总结而来,未能解释其内在机理[1]。本文将基于ST定理对其进行分析,揭示其内在规律。ST定理描述了声速剖面面积与传播时间的关系[25],可以将其表示为
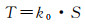 (1)
(1)
式中,T是瞬时声速剖面下声波从声源到达海底应答器经历的时间;S是瞬时声速剖面面积;k0是常系数,在背景声速剖面一定的条件下,仅与初始入射角有关。
瞬时声速剖面是难以获得的,通常用于声线跟踪法的是实际测量获得的某一固定声速剖面,同样基于ST定理可得
 (2)
(2)
式中,T′是实测声速剖面下声波从声源到达应答器经历的时间;S′是实测声速剖面面积。由此可知T与T′的差即是由声速剖面测量的不准确所引起的测时误差。
将瞬时声速剖面面积S看成由背景声速剖面面积Sb和瞬时声速剖面面积的变化量ΔS组成,将实测声速剖面面积S′看成由背景声速剖面面积Sb和两者之差ΔSb组成,若近似的认为测距误差是测时误差与底层海水声速的乘积,则将式(1)和式(2)做差得到测距误差的近似表达式
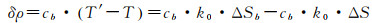 (3)
(3)
式中,cb是海底声速值。从式(3)可以看出测距误差可以认为由两部组成,前一项cb·k0·ΔSb是背景声速剖面误差,由于ΔSb是常量,所以在k0不变的情况下,这一项测距误差为常数。后一项cb·k0·ΔS是测距误差的周期项,在k0一定的情况下,它的变化规律与ΔS相同。
根据以上分析可知,声速的不确定性引起的误差包括背景声速剖面误差、误差长周期项和误差短周期项。对于周期性的误差,若能保证观测数据的时间跨度相比于误差周期项的周期足够长,且观测量足够多,那么在计算控制点坐标的最或然值时,周期项误差对坐标解算偏差的影响将被消除,这种手段适用于误差短周期但不适用于误差长周期项,因为误差长周期项的周期为一天,很难保证连续几天时间跨度的观测,而短周期的周期为几分钟到几小时,相比之下更容易满足。为消除背景声速剖面误差和误差长周期项的影响,本文进行如下设计,设计测量船的走航策略为两应答器的中垂线,这样可以保证测量船到两应答器的距离时时相等,因距离相等,这两项误差数值相同,对同一时刻两观测方程做差可消除其影响。
2 深海海底控制点绝对坐标的解算方法根据对声速不确定性引起测距误差的分析,海底控制点定位的观测方程可以写成
 (4)
(4)
式中,ρij是第i次测量船底换能器到海底应答器j的距离观测值;f( )表示两点之间直线距离;xi是测量船上船底换能器在第i次测量时的三维坐标;xoj是海底应答器j在海底的三维坐标;δρd是应答器固有测距误差;δρvb是由背景声速剖面测量不准确所引起的测距误差;δρvl是潮汐,温度日变化所引起的测距误差长周期项;δρvs是由内波引起的测距误差短周期;εi是随机误差。
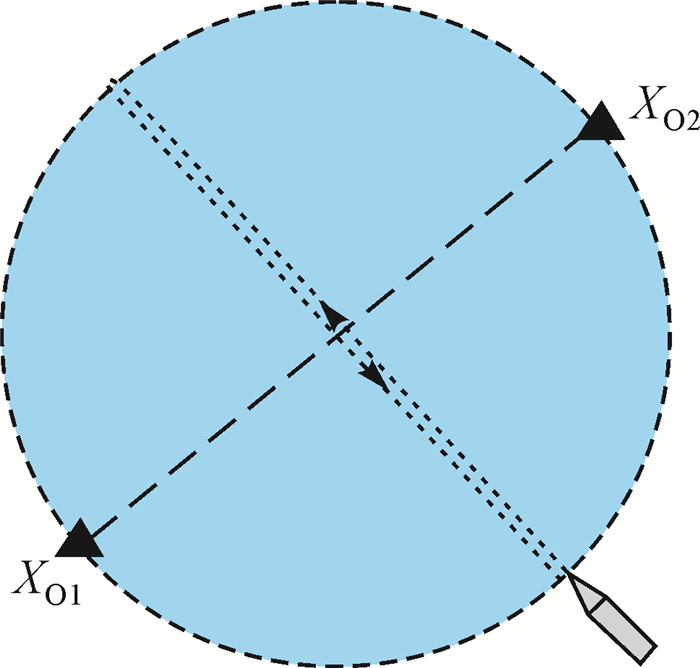
基于前文对测距误差的分析,本文设计测量船的航迹为两应答器的中垂线,如图 1所示。其中黑色三角形是海底应答器的位置,垂直于应答器连线的虚线是测量船走航的航迹。这样设计的好处在于每次采样时,测量船到两应答器的距离近似相等,测距误差δρd、δρvb、δρvl相等,利用差分的方法可将其消除,残余的测距误差短周期项和随机项可认为是附加在δρd、δρvb、δρvl之上的扰动项,通过多次观测予以消除,下面是基于此思想所建立的控制点定位解算模型。
|
| 图 1 测量船走航航迹 Fig. 1 The trajectory of the survey ship |
根据式(4)可得任一观测时刻测量船分别到应答器XO1和XO2的观测方程
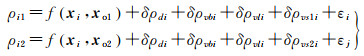 (5)
(5)
将式(5)中的两式线性化展开后得
 (6)
(6)
式中, ρi10和ρi20分别是观测量ρi1和ρi2的近似值;lo1i=(xi-xo1)/ρi10; mo1i=(yi-yo1)/ρi10;no1i=(zi-zo1)/ρi10;lo2i=(xi-xo2)/ρi20;mo2i=(yi-yo2)/ρi20;no2i=(zi-zo2)/ρi20;(xo1, yo1, zo1)和(xo2, , yo2, zo2)分别是应答器XO1和XO2的近似坐标;dxo1、dyo1、dzo1、dxo2、dyo2、dzo2, 是应答器XO1和XO2的三维坐标改正数。将式(6)两式做差可得
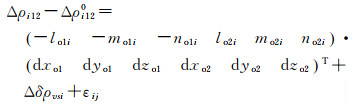 (7)
(7)
式中,Δρi12=ρi1-ρi2;Δρi120=ρi10-ρi20;Δδρvsi=Δδρvsli-Δδρvs2i, 事实上由内波引起的测距误差短周期项Δδρvsi很难消除,但是通过多次观测计算坐标改正数的最或然值可降低其影响,式(7)可写成误差方程矩阵的形式
 (8)
(8)
式中dx=[dxo1 dyo1 dzo1 dxo2 dyo2 dzo2];L=[Δρ112-Δρ1120 Δρ212-Δρ2120…Δρn12-Δρn120],B是系数阵。
压力传感器在深海的测深值不准确,但是控制点之间的深度差却可以精确的获得,同时圆走航的方法已经实现计算控制点的水平坐标可以达到厘米级的精度,因此本文在上述差分方法的基础上又附加了控制点间水平距离和深度差约束,这两项限制条件可表示为
 (9)
(9)
 (10)
(10)
式中,h为应答器的水平距离;Δz12是应答器间的深度差,限制条件方程可写为
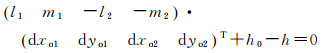 (11)
(11)
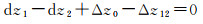 (12)
(12)
式中,Δz0是Δz12的近似值;h0是h的近似值;l1=(x1-xo1)/h0;l2=(x2-xo2)/h0;m1=(y1-yo1)/h0;m2=(y2-yo2)/h0。将式(11)和式(12)写成矩阵形式
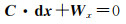 (13)
(13)
式中,

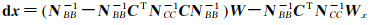 (14)
(14)
式中,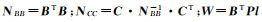
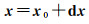 (15)
(15)
单位权中误差的无偏估值为
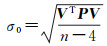 (16)
(16)
控制点XO1和XO2的点位中误差是
 (17)
(17)
 (18)
(18)
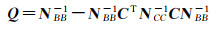 (19)
(19)
为验证新方法的有效性,本文进行了如下仿真试验,仿真试验的条件设计如下:坐标系选用笛卡尔坐标系,两应答器连线的中点在海面的投影位置是坐标原点,x轴指向东,y轴指向北,z轴指向天顶。水深设置为3000 m,应答器布放于海底,坐标分别为XO1(-1500, -1500, -3000)和XO2(1500, 1500, -2998),测量船航迹设计如图 1所示,速度6节(约3 m/s),每10 s实施一次水声测距。除此之外,设置潮汐的周期为12 h,振幅为5 m, 海面波浪的周期为20 s,振幅为2 m。测量船水平方向的定位精度为5 cm,垂直方向定位精度为10 cm,两应答器的参考深度偏差分别设置为1 m和1.2 m。
试验中背景声速剖面用Munk的标准方程构建[26]
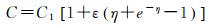 (20)
(20)
 (21)
(21)
式中,C1=1482 m/s是声道轴处的声速;Z1=1000 m是声道轴的深度;ε=7.4×10-3是扰动系数;B=1300是声道尺度厚度,仿真所得声速剖面如图 2所示;若设置声道尺度厚度B=1299,得到的声速剖面当作实测声速剖面,图 2右图为两声速剖面之差。
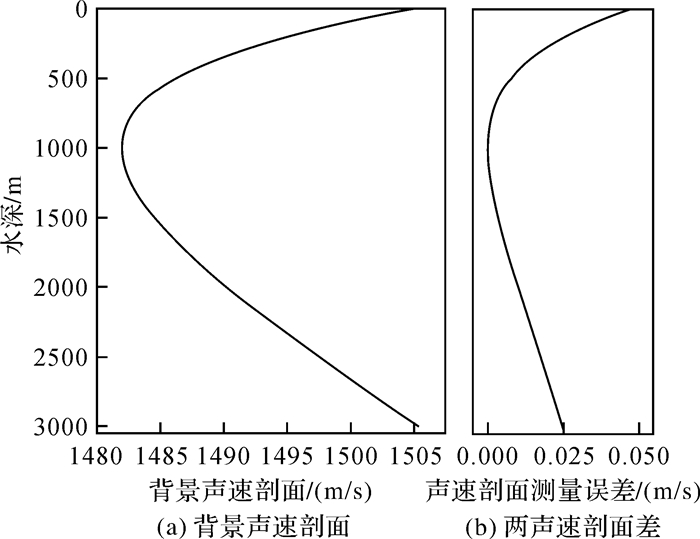
|
| 图 2 仿真所得声速剖面 Fig. 2 Sound velocity profile abtained by simulation |
实际海洋中声速剖面不断随时间变化,本文根据文献[27—28]的方法仿真了温度日变化和内波引起的声速剖面变化的部分,分别代表声速剖面的长周期和短周期变化,结果如图 3和图 4。
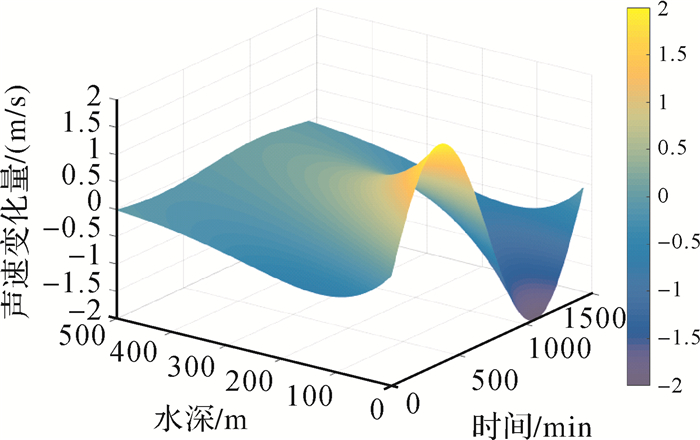
|
| 图 3 温度日变化引起的声速剖面变化 Fig. 3 Variation of sound velocity profile caused by diurnal temperature variation |

|
| 图 4 内波引起的声速剖面变化 Fig. 4 Variation of sound velocity profile caused by internal waves |
因为瞬时声速剖面已知,换能器到应答器的相对位置已知,所以观测量传播时间采用文献[20]的方法计算,利用常梯度声线跟踪法,不断调整初始入射角,当声线到达位置与应答器的位置之间的距离小于某一限差时,对应的传播时间即为所求的观测量,在此观测量基础上再附加RMS为5 μs的随机测量误差得到最终传播时间观测值。实际计算测距值是利用此观测量、应答器参考深度、包含误差的某一实测声速剖面(式(20),B=1299计算所得的声速剖面),根据牛顿迭代法计算。
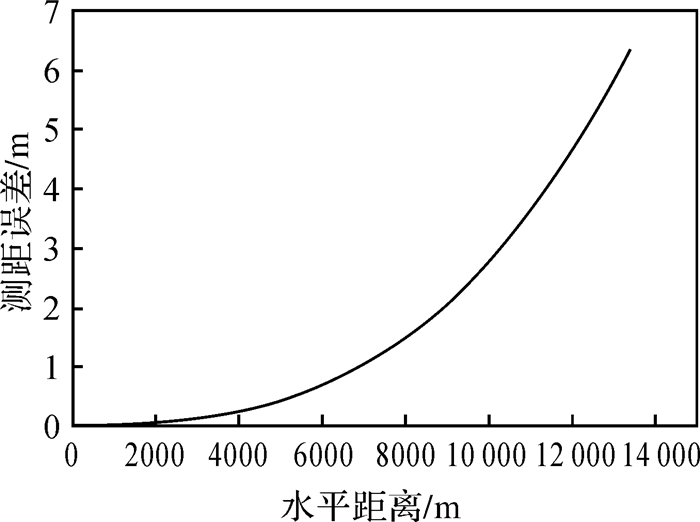
根据Munk方程构建的声速剖面来验证第2小节的结论,首先验证背景声速测量误差引起的测距误差与海底应答器到船底换能器水平距离关系,试验中不附加其他因素的影响,只考虑背景声速测量误差,结果如图 5所示。
|
| 图 5 背景声速剖面误差引起的测距误差与水平距离的关系 Fig. 5 Relationship between range error caused by background sound velocity profile error and horizontal distance |
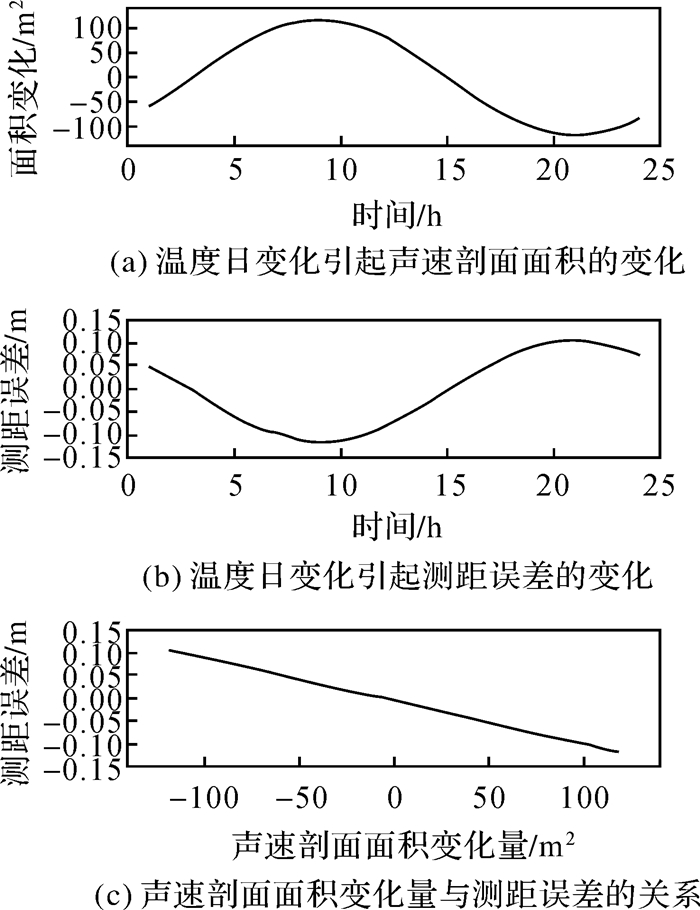
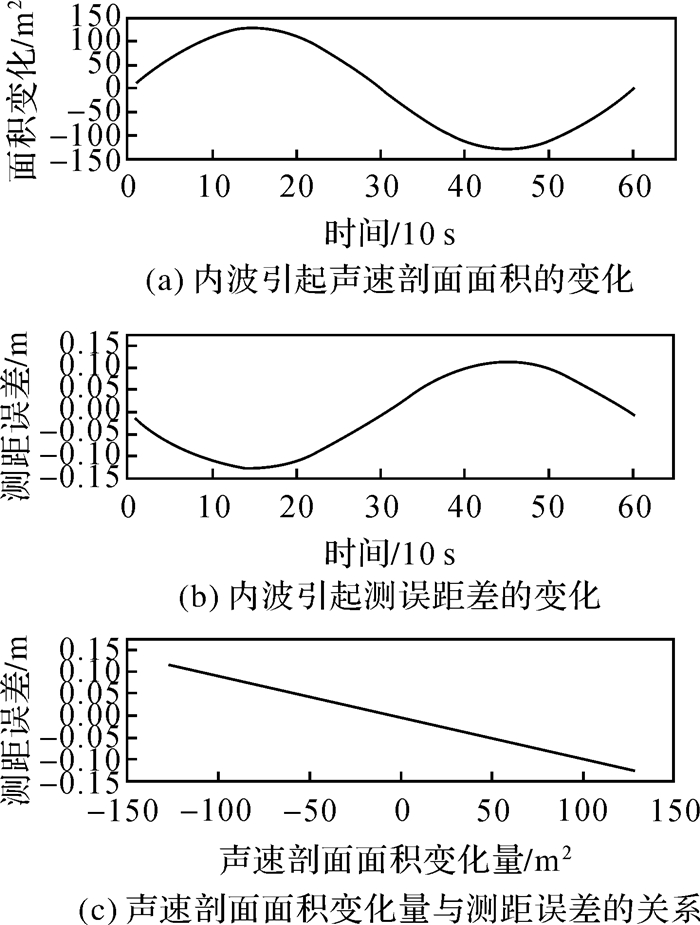
从图 5中可以看出测距误差及其增幅都随应答器到换能器水平距离的增大而增加。第2小节的分析得出结论测距误差的变化规律与声速剖面面积的变化规律相同,基于本节所设置的仿真试验条件,设置船底换能器和海底应答器的水平距离不变,对上述关于温度日变化和内波对测距误差规律影响的结论加以证明,结果如图 6和图 7所示。
|
| 图 6 温度日变化影响 Fig. 6 The influence of diurnal temperature rariation |
|
| 图 7 内波影响 Fig. 7 The influence of internal waves |
从图 6和图 7可以看出,仿真试验结果验证了声速剖面面积与传播时间存在线性关系,同时也验证了测距误差的变化规律与声速剖面面积的变化规律相同的结论,而且两者具有相同的周期,在对测距误差的变化规律分析完之后,开始对新方法有效性的验证。
本文采用目前最常用的圆走航确定水下控制点坐标的方法作为对照试验[29],测量船圆走航的半径与水深相等,单个应答器测量时间约2 h(测量船走航一圈),共获得720个采样点,两应答器的坐标偏差计算结果见表 1。
| cm | |||
| 应答器 | dx | dy | dz |
| XO1 | 3.3 | -6.5 | -35.7 |
| XO2 | 3.7 | -6.4 | -36.4 |
从表 1可以看出,应答器坐标水平解的准确度高于垂直解一个数量级,表明圆走航的方法可以减小声速误差对水平坐标解的影响,但垂直解依旧较差,这与圆走航消除水平方向误差的设计相吻合,也已被国内外研究所证实。下面采用本文方法,测量船按所设计好的测线(图 1)走航4 h,共获得1440个采样点。两应答器三维坐标的解算结果见表 2。
| cm | |||
| 应答器 | dx | dy | dz |
| XO1 | 1.1 | -4.0 | -10.1 |
| XO2 | 1.4 | -3.8 | -9.3 |
表 2的结果表明,本文方法相比于圆走航无论水平解或是垂直解的偏差都得到了改善,相比之下,垂直解的改善更加明显和有意义,垂直坐标的解算偏差由圆走航30几个cm的偏差提高到了10 cm左右。圆走航能够提高控制点水平方向坐标偏差的原因在于对观测点空间分布的优化,在确保应答器到各观测点距离相同的情况下,各主要因素引起的测距误差近似相等,因此水平方向的误差相互抵消,得到控制点坐标水平解的准确度较高。然而测量船始终处于海面,应答器布放于海底,控制点坐标垂直方向准确度的提高是无法通过优化观测点空间分布的方法实现的,因此控制点坐标垂直解的偏差要远大于水平解。与圆走航方法不同,本文方法在优化了观测点空间分布的基础上,又利用差分的思想消除了主要测距误差项,同时又附加了两项约束作为限制条件,使得控制点垂直解偏差的准确性得到了较好的改善。
4 结语本文针对确定深海海底控制点三维绝对坐标垂直解偏差大的问题,分析了声速剖面不确定性对测距误差的影响,设计了适合深海海底控制点坐标确定的测量船走航策略,并提出了附加控制点间深度差和水平距离约束的差分定位算法,通过理论分析和试验验证得出了以下结论:
(1) 声速剖面的不确定性引起的测距误差包括背景声速剖面误差、误差的长周期项和误差的短周期项;声速剖面面积与周期项测距误差具有相同的变化规律和周期;
(2) 本文提出的附加应答器水平距离和深度差约束的水下差分定位模型,相比于目前认可度较高的圆走航方法,控制点坐标水平解和垂直解的偏差都有所减小,特别是垂直解的偏差得到了较大的改善,验证了该方法的有效性。
| [1] | SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/Acoustic positioning of seafloor reference points for tectonic studies[J]. Physics of the Earth and Planetary Interiors, 1998, 108(2): 101–112. DOI:10.1016/S0031-9201(98)00089-2 |
| [2] | CHADWELL C D, SPIESS F N, HILDEBRAND J A, et al. Sea floor strain measurement using GPS and acoustics[M]//SEGAWA J, FUJIMOTO H, OKUBO S. Gravity, Geoid and Marine Geodesy. Berlin, Heidelberg: Springer, 1997: 682-689. |
| [3] | GORDON R G, STEIN S. Global tectonics and space geodesy[J]. Science, 1992, 256(5055): 333–342. DOI:10.1126/science.256.5055.333 |
| [4] | FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/Acoustic seafloor geodetic observation:method of data analysis and its application[J]. Earth Planets & Space, 2006, 58(3): 265–275. |
| [5] | KUSSAT N H, CHADWELL C D, ZIMMERMAN R. Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements[J]. IEEE Journal of Oceanic Engineering, 2005, 30(1): 153–164. DOI:10.1109/JOE.2004.835249 |
| [6] | MATSUMOTO Y, FUJITA M. Combined GPS/acoustic seafloor geodetic observation system by japan coast guard[J]. Journal of the Geodetic Society of Japan, 2006, 52(4): 273–283. |
| [7] | GAGNON K, CHADWELL C D, NORABUENA E. Measuring the onset of locking in the Peru-Chile trench with GPS and acoustic measurements[J]. Nature, 2005, 434(7030): 205–208. DOI:10.1038/nature03412 |
| [8] | WATANABE S I, ISHIKAWA T, YOKOTA Y. Non-volcanic crustal movements of the northernmost Philippine Sea plate detected by the GPS-acoustic seafloor positioning[J]. Earth, Planets and Space, 2015(67): 184. |
| [9] | SPIESS F N. Suboceanic geodetic measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 1985, GE-23(4): 502–510. DOI:10.1109/TGRS.1985.289441 |
| [10] | ZHAO Jianhu, ZOU Yajing, ZHANG Hongmei, et al. A new method for absolute datum transfer in seafloor control network measurement[J]. Journal of Marine Science and Technology, 2016, 21(2): 216–226. DOI:10.1007/s00773-015-0344-z |
| [11] | OSADA Y, FUJIMOTO H, MIURA S, et al. Estimation and correction for the effect of sound velocity variation on GPS/Acoustic seafloor positioning:an experiment off Hawaii Island[J]. Earth, Planets and Space, 2003, 55(10): e17–e20. DOI:10.1186/BF03352464 |
| [12] | FUJIMOTO H, KANAZAWA T, MURAKAMI H. Seafloor acoustic ranging and the effect of temperature variation[M]//SEGAWA J, FUJIMOTO H, OKUBO S. Gravity, Geoid and Marine Geodesy. Berlin, Heidelberg: Springer, 1997: 690-695. |
| [13] | National Research Council Panel on Crustal Movement Measurements. Geodetic monitoring of tectonic deformation: toward a strategy[R]. Washington, DC: National Academy Press, 1981. |
| [14] | XU Peiliang, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795–808. DOI:10.1186/BF03351859 |
| [15] | ASADA A, YABUKI T. Centimeter-level positioning on the seafloor[J]. Proceedings of the Japan Academy, Series B, 2001, 77(1): 7–12. DOI:10.2183/pjab.77.7 |
| [16] | YANG Fanlin, LU Xiushan, LI Jiabiao, et al. Precise positioning of underwater static objects without sound speed profile[J]. Marine Geodesy, 2011, 34(2): 138–151. DOI:10.1080/01490419.2010.518501 |
| [17] |
韩云峰, 郑翠娥, 孙大军.
长基线定位系统高精度阵型标定方法[J]. 声学学报, 2016, 41(4): 456–464.
HAN Yunfeng, ZHENG Cui'e, SUN Dajun. A high precision calibration method for long baseline acoustic positioning systems[J]. Acta Acustica, 2016, 41(4): 456–464. |
| [18] |
赵建虎, 邹亚靖, 吴永亭, 等.
深度约束的海底控制网点坐标确定方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 137–141.
ZHAO Jianhu, ZOU Yajing, WU Yongting, et al. Determination of underwater control point coordinate based on constraint of water depth[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 137–141. DOI:10.11918/j.issn.0367-6234.2016.10.020 |
| [19] |
赵建虎, 陈鑫华, 吴永亭, 等.
顾及波浪影响和深度约束的水下控制网点绝对坐标的精确确定[J]. 测绘学报, 2018, 47(3): 413–421.
ZHAO Jianhu, CHEN Xinhua, WU Yongting, et al. Determination of absolute coordinate of underwater control point taking waves and depth's constraint into account[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 413–421. DOI:10.11947/j.AGCS.2018.20170246 |
| [20] | CHADWELL C D, SWEENEY A D. Acoustic ray-trace equations for seafloor geodesy[J]. Marine Geodesy, 2010, 33(2-3): 164–186. DOI:10.1080/01490419.2010.492283 |
| [21] | SWEENEY A D, CHADWELL C D, HILDEBRAND J A, et al. Centimeter-level positioning of seafloor acoustic transponders from a deeply-towed interrogator[J]. Marine Geodesy, 2006, 28(1): 39–70. |
| [22] | SAUNDERS P M, FOFONOFF N P. Conversion of pressure to depth in the ocean[J]. Deep Sea Research and Oceanographic Abstracts, 1976, 23(1): 109–111. DOI:10.1016/0011-7471(76)90813-5 |
| [23] | SAUNDERS P M. Practical conversion of pressure to depth[J]. Journal of Physical Oceanography, 1981, 11(4): 573–574. DOI:10.1175/1520-0485(1981)011<0573:PCOPTD>2.0.CO;2 |
| [24] | YAMADA T, ANDO M, TADOKORO K, et al. Error evaluation in acoustic positioning of a single transponder for seafloor crustal deformation measurements[J]. Earth, Planets and Space, 2002, 54(9): 871–881. DOI:10.1186/BF03352435 |
| [25] | SUN Wenzhou, YIN Xiaodong, ZENG Anmin. The relationship between propagation time and sound velocity profile for positioning seafloor reference points[J]. Marine Geodesy, 2019, 42(2): 186–200. DOI:10.1080/01490419.2019.1575938 |
| [26] | MUNK W H. Sound channel in an exponentially stratified ocean, with application to SOFAR[J]. The Journal of the Acoustical Society of America, 1974, 55(2): 220–226. DOI:10.1121/1.1914492 |
| [27] |
吕华庆.
物理海洋学基础[M]. 北京: 海军出版社, 2012.
LÜ Huaqing. Fundamentals of marine physics[M]. Beijing: Navy Press, 2012. |
| [28] |
刘进忠, 王宁, 高大治.
浅海内波及声场起伏数值研究[J]. 中国海洋大学学报, 2005, 35(2): 317–324, 224.
LIU Jinzhong, WANG Ning, GAO Dazhi. Ocean internal waves in ASIAEX 2001 and Numerical simulation of sound propagation[J]. Periodical of Ocean University of China, 2005, 35(2): 317–324, 224. |
| [29] | KUSSAT N H, CHADWELL C D, ZIMMERMAN R. Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements[J]. IEEE Journal of Oceanic Engineering, 2005, 30(1): 153–164. DOI:10.1109/JOE.2004.835249 |


