受复杂海洋环境、系统噪声和测量船噪声等影响,获取的测深数据有时会在某一区域产生大面积的异常值。这些异常值通常会被人为删除,从而造成某一区域连续的数据缺失,严重影响测深数据对海底地形的准确描述,不利于海底趋势面的构造。专家学者在水深测量领域做了很多研究[1-5],并通过加权平均值[6-7]、AR模型[8]、统计学原理[9-10]、中值滤波[11]、不确定度及Kalman滤波[12-14]等算法对海量的测深数据进行处理,识别并剔除异常值。虽然现有算法已经取得了较好的效果,但对于海量测深数据仍存在处理速度慢、适用性较差、复杂海床测深数据滤波性能欠佳、海岸线及岛礁附近水域精度不高等不足。同时,基于“平均”的原理,一些算法对于大面积异常值会处理为“伪海底高山”或“伪海底低谷”。基于上述情况,本文提出了利用条件变分自编码生成对抗网络方法,检测并消除伪地形数据。
近年来,生成式对抗网络(GAN)作为一种生成式建模方法被应用于多个领域,许多学者做了大量的工作[15-20]。在生成式对抗网络中,生成器和判别器为博弈双方。生成器拟合数据的产生过程生成模拟样本,优化目标为纳什均衡[21],用于估测数据样本的分布规律[22]。GAN目前已经应用于图像识别、语音和语言处理、人工智能下棋等问题的研究中。然而,GAN在海底地形数据处理领域的应用目前还比较缺乏,虽然现有滤波算法等已经有了较好的效果,但当噪声较为复杂,尤其是在产生大面积测深数据异常值的情况下并不能很好地重建海底地形趋势面。本文结合条件变分自编码和深度卷积生成对抗网络,建立条件变分自编码生成对抗网络,利用该网络模型的判别器提取海底地形的特征,对含有大面积伪地形的海底地形样本数据进行检测与剔除。试验结果表明,本文方法能够较为有效地检测和剔除大面积异常值,并生成较为合理的海底趋势面。
1 条件变分自编码器原理自编码器(autoencoder)是一种以重构输入信号为目标的神经网络。对于条件变分自编码器而言,该网络通过从编码样本分布pmodel(h)中采样生成g(h),再从符合pmodel(x|g(h)=pmodel(x|h)的分布条件中取样x,经过重构的解码器r=m(h)构成网络。编码器网络为随机映射m(h|x),解码器网络为随机映射pmodel(x|h)。
对于条件变分自编码器而言,该算法通过将x与样本相关联的变分下界γ(m)最大化对模型进行训练,具体为式(1)所示
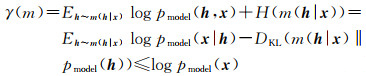 (1)
(1)
式中,DKL为KL散度,可以用于衡量同一随机变量的两个单独概率分布的差异。
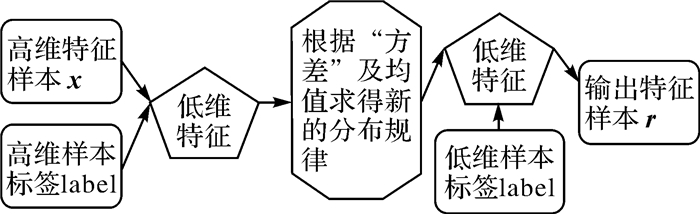
本文采用的变分自编码器加入标签项作为限制,即条件变分自编码网络。该网络共包含4个全连接层,具体结构如图 1所示。
|
| 图 1 标签限制的变分自编码网络(CVAE)结构 Fig. 1 Label-restricted conditional variational autoencoder network structure |
2 深度卷积生成对抗网络原理
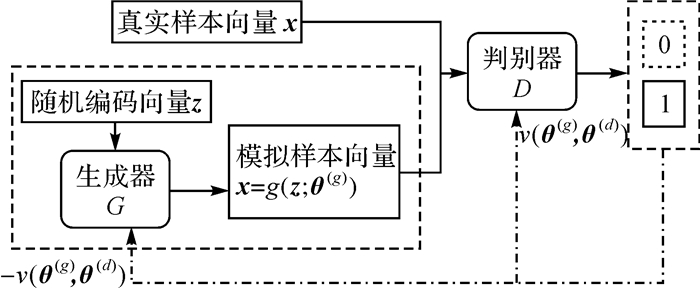
生成式对抗网络是基于可微生成器网络的另一种生成式建模[15-16]。基于博弈论(game theory)场景,GAN的基本结构为:生成器(generator network, G)直接产生样本x=g(z; θ(g)),z为随机编码向量。其对手判别器(discriminator network, D)发出由d(x; θ(d)))给出的概率值,通过训练不断提高区分从训练数据抽取的样本和从生成器抽取的样本的能力,指示x是真实训练样本而不是从模型抽取的伪造样本的概率。GAN的网络结构如图 2所示。
|
| 图 2 GAN网络结构 Fig. 2 Generative adversarial network structure |
GAN的优化问题是一个极小极大博弈问题,函数v(θ(g), θ(d))确定判别器的收益,生成器接收-v(θ(g), θ(d))作为它自己的收益。因此,在式(2)收敛
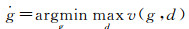 (2)
(2)
式中,v(θ(g), θ(d))=Ex~pdata log d(x)+Ex~pmodel log(1-d(x))。
基于深度卷积的GAN(DCGAN)[17],是将CNN卷积用于GAN模式的网络里,生成器G通过反卷积的重构技术来模拟原始数据,而判别器D利用卷积技术学习海底地形数据的特征,进而作出判断。
3 基于条件变分自编码生成对抗网络的大面积伪地形数据检测与剔除 3.1 条件变分自编码生成对抗网络模型结构综合CVAE和DCGAN网络的特点,建立两者相结合的模型——条件变分自编码生成对抗网络模型。在该模型中,编码器对被破坏的原始图像进行编码、降维;解码器(也叫重构器),通过重构一部分输入的特征来确定与样本互信息的维度,从而找出主要特征,并作为输入进入生成器;生成器从标准高斯分布中随机采样作为输入的生成模拟样本,并将噪声分成不可压缩噪音z和可解释性信息c;判别器用深度卷积神经网络对生成模拟数据与真实样本数据进行判别。加入条件变分自编码网络后,提高了从高维到低维映射的能力。具体网络结构如图 3所示。

|
| 图 3 条件变分自编码生成对抗网络结构 Fig. 3 Conditional variational autoencoder generative adversarial network |
3.2 CVAE-GAN模型在大面积伪地形数据检测与剔除问题上的应用
条件变分自编码生成对抗网络是根据有限的样本信息在地形特征的复杂性和学习能力之间寻求平衡点。利用CVAE-GAN构造海底趋势面的效果主要取决于选区的训练样本及优化算法的选取是否真正反映海底地形的实际变化。
3.2.1 训练样本的选取由于浅水多波束测深系统或者深水多波束测深系统均以广角度定向发射、多阵列信号接收处理的方式,获得的海底水深数据具有海量性的特点,因而要对测深数据进行区域划分。选择的区域过大,导致包含的海底地形类型过多,样本分布规律过于复杂;选择的区域过小,无法学习到整体的地形变化趋势。本文按照陡坡、海岸带、岛礁、海沟及碎石区5种不同的地形选取水深格网数据作为样本,以人为添加异常值数据来模拟格网化的含有异常值的原始水深数据;以未添加异常值的水深格网数据来模拟真实地形数据。共设置为6类(第0类到第5类),通过数据集增强方法,得到训练样本每类包含1000个图片,共6000张图片。在测试样本中,含有大面积连续异常值的格网水深数据,每类包含1张图片共6张,并对数据进行归一化处理。
3.2.2 优化算法的选取除了高效地选取样本,还必须选择适合海底地形变化的优化算法。针对不同特点的样本数据,不同的优化算法,其收敛速度和快速找到收敛最快方向的能力不同。凸问题优化算法,如AdamGrad算法,缩放参数反比于其所有梯度历史平方值总和的平方根[23]。非凸问题优化算法,如Adam算法[24],梯度积累为指数加权的的移动平均,同时设置了偏置修正,更加稳健。由于海底地形并不是凸问题,故本文选择Adam优化算法。经验表明,当模型数据较为复杂时,Adam算法的初始学习率设置为0.001,在Tensorflow系统体系中优化效果最好。
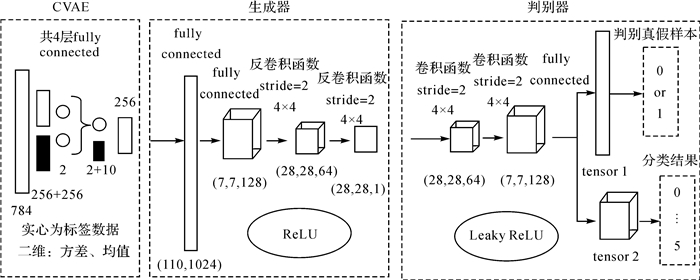
3.2.3 模型训练过程基于数据集增强的原理,将符合标准高斯分布的噪声加入到训练样本中,通过编码器降维;通过KL散度求得训练样本分布与标准高斯分布之间的对应差距,并逐步缩小该差距,改变样本的对应分布;通过解码器最终学习到样本分布规律并生成模拟样本,在此过程中,使用样本标签作为限制。由条件变分自编码网络生成的拟真实样本进入生成器后,通过两层使用ReLU作为激活函数的全连接层,生成(7, 7, 128)的三维张量,进入卷积核4×4、步幅为2的反卷积函数层,经过中间层三维张量(28, 28, 64)得到三维张量(28, 28, 1)的生成图像样本。进入判别器,首先经过两层与生成器反卷积核成转置关系的卷积层得到(7, 7, 128)的三维张量,使用LeakyReLU作为激活函数与生成器对抗,并通过两层全连接层,分别得到两个张量,将这两个张量放入不同输出层可用于判别真假样本、进行样本分类以及得到隐含信息。基于信息论的相关理论,网络中的损失函数采用交叉熵(cross-entropy),最小化该交叉熵将执行对分类器的最大似然估计,结构如图 4所示。
|
| 图 4 CVAE-GAN具体结构 Fig. 4 Detailed CVAE-GAN structure |
3.2.4 训练结果与分析
本文人为添加了大面积伪地形数据,生成测试数据集,对伪地形进行检测和剔除,构建了CVAE-GAN网络模型进行测试。试验环境为Intel(R) Core(TM) i7-8550U CPU @ 1.8 GHz处理器,8 GB原始运行内存(RAM),Tensorflow平台。在Leaky ReLU中,模型的leak斜率为0.1。
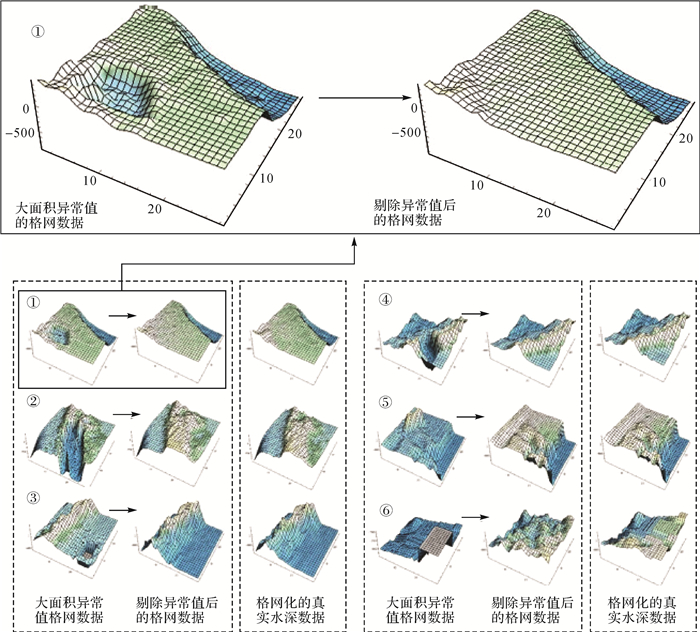
本文采用仿真的水深格网数据进行评估。该水深格网数据分辨率为5 m,每组数据代表的测区面积为19 600 m2,共包含陡坡、海岸带、岛礁、海沟及碎石区5个不同特征的地形构造。每种地质构造的“大面积伪地形”数据约占测区总数据的3%~5%,具体特点为:①“陡坡”异常值出现于较平坦区域;②“海岸带”异常值出现于海陆交界处;③“岛礁1”异常值出现于较平坦区域;④“岛礁2”异常值出现于岛礁凸起处;⑤“海沟”异常值表现为大面积区域水深整体变深;⑥“碎石区”异常值表现为缺失大面积水深数据,具体如图 5所示。
|
| 图 5 各类海底微地形数据的大面积异常值检测与剔除点集三维图 Fig. 5 Training process in different types of sea bottom |
为了进一步分析该模型在大面积异常值检测方面的精度,分别绘制不同模型下的海底地形等深线图和与真实水深值对比得到的误差等值线图,具体如图 6所示。

|
| (图中相关要素及数据均为虚构) 图 6 等值线图 Fig. 6 Contour map |
在生成对抗的过程中,经过5次反复训练,共10 000次迭代。观察生成图像的演变过程,从图 5、图 6可以看出,含有大面积异常值的格网水深数据,通过本文方法,逐步学习不同类型的地形特征,通过10 000次迭代,最终达到较好的异常值剔除效果。从图 5、图 6可以看出,不同的海底地形特征得到的海底趋势面的准确度不同,陡坡、海岸带、岛礁及海沟等具有明显海底地形特征的区域生成的海底趋势面精度更高,而碎石区等海底地形特征不明显的区域生成效果会产生多余的噪声。在图 5、图 6中,过程最后一张为结果图,从中可以看出该方法具有较强的识别度,秩值更低,且与训练样本保持着高度的相似,通过学习找到真实海底地形中更加明显的特征规律。因此,CVAE-GAN网络可以用于大面积伪地形数据的检测与剔除。
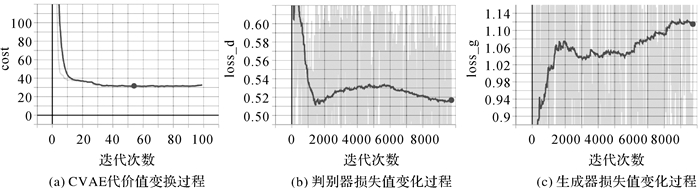
模型在训练过程中的损失函数曲线如图 7所示。图 7(a)的橫坐标为条件变分自编码的迭代次数,纵坐标为代价函数值;图 7(b)、(c)中的橫坐标分别为判别器与生成器的迭代次数,纵坐标为其损失函数。可以看出条件变分自编码模型的代价函数,生成模型和判别模型的损失函数都在逐渐收敛,并存在着明显的相互关系。随着迭代的进行,条件变分自编码网络的代价函数在逐渐下降,由最初值97.45下降至30.58;判别器的损失函数由最初值0.613 6下降至0.346 3;生成器的损失函数则逐渐上升,由最初值0.851 2上升至1.490,在对抗中此消彼长,共历时35 min,迭代10 000次。通过条件变分自编码网络能够改变测试样本的概率分布,结合生成对抗网络,CVAE-GAN模型可以更好地使用学习到的训练样本分布特征,有效提高了网络的稳定性和泛化能力。
|
| 图 7 数据集迭代过程中损失函数变化过程 Fig. 7 The loss function curves of the model |
本文将CVAE-GAN与其他两种常用的测深数据异常值检测方法(中值滤波法、趋势面滤波法[1-2])对比。采用4种不同的评价指标对异常值检测与剔除效果进行评定:①梯度均方根误差(DRMSE)——用不同方法得到的海底格网数据(生成数据)的梯度求均方根误差,具体如式(3)所示;②最大梯度差(DMAX)——用生成数据的梯度与真实格网水深数据的梯度求差的最大值,具体如式(4)所示;③峰值信噪比(peak signal to noise ratio, PSNR),值越大,生成数据与真实格网水深数据越相似,具体如式(5)、式(6)所示;④结构相似指数(structural similarity index, SSIM)——将生成数据的均值、梯度和结构3种不同因素组合建模,值在-1至1之间,越接近于1,说明生成数据与真实格网数据的结构越相似,具体如式(7)—式(9)所示。
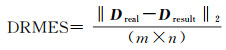 (3)
(3)
 (4)
(4)
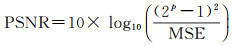 (5)
(5)
 (6)
(6)
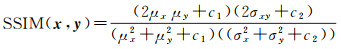 (7)
(7)
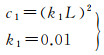 (8)
(8)
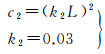 (9)
(9)
式中,Dreal为格网化的真实水深数据的梯度;Dresult为生成数据的梯度;p为每个采样值所占的比特数;x为格网化的真实水深数据;y为生成数据;μx、μy为平均值;σx、σy为标准差;σxy为协方差;c1、c2用于维持该式的稳定;m、n为矩阵的行数和列数。不同模型的“评价指标”比较见表 1。
| 检测 方法 |
海底 地形 |
评价指标 | |||
| DRMSE | DMAX | PSNR | SSIM | ||
| 中值滤波法 | 陡坡 | 0.005 | 0.335 | 17.642 | 0.347 |
| 海岸带 | 0.008 | 0.940 | 10.112 | 0.089 | |
| 岛礁1 | 0.004 | 0.433 | 8.200 | 0.216 | |
| 岛礁2 | 0.006 | 0.701 | 15.284 | 0.297 | |
| 海沟 | 0.003 | 0.253 | 14.871 | 0.341 | |
| 碎石区 | 0.013 | 0.834 | 15.020 | 0.060 | |
| 趋势面滤波法 | 陡坡 | 0.013 | 0.748 | 9.718 | 0.280 |
| 海岸带 | 0.010 | 0.871 | 10.391 | -0.051 | |
| 岛礁1 | 0.006 | 0.660 | 4.508 | -0.074 | |
| 岛礁2 | 0.009 | 0.770 | 10.350 | 0.217 | |
| 海沟 | 0.011 | 0.741 | 11.421 | 0.298 | |
| 碎石区 | 0.008 | 0.866 | 9.646 | 0.036 | |
| 本文方法 | 陡坡 | 0.003 | 0.280 | 23.900 | 0.521 |
| 海岸带 | 0.002 | 0.254 | 28.238 | 0.805 | |
| 岛礁1 | 0.002 | 0.245 | 17.166 | 0.504 | |
| 岛礁2 | 0.002 | 0.250 | 24.695 | 0.776 | |
| 海沟 | 0.001 | 0.223 | 22.450 | 0.685 | |
| 碎石区 | 0.007 | 0.533 | 12.549 | 0.117 | |
从表 1可以看出,当海底地形测量出现大面积集中分布的异常值而不是随机分布的较少量的异常值时,本文方法的检测与剔除效果比中值滤波法及趋势面滤波法的效果好。根据表 1,中值滤波在进行异常值剔除过程中,由于异常值的数量多且集中的特点,过度平滑了区域整体的海底地形,导致海底地形趋势面的失真,使得梯度的均方根误差较大,PSNR值较小,SSIM值距离1较远;趋势面滤波由于多项式拟合无法详细表示复杂的地形,或者“过拟合”,将异常值也作为正常水深数据,导致误差较大。本文方法在除去大量连续异常值的过程中,能够较好地保存其余的原始地形形态,梯度的均方根误差较小,PSNR值较大,SSIM值更接近于1。中值滤波的过度平滑导致海底地形坡度偏大或偏小,即容易出现海底“断崖”等现象;趋势面滤波受制于多项式拟合的局限性,对于有些复杂的海底地形无法拟合出合理的海底趋势面;本文方法通过“变分”思想,学习训练样本分布规律,对不同区域有不同的生成过程,不会“以偏概全”,从而能够更好地剔除大量连续异常值。综上所述,在检测并剔除大面积“伪地形”方面,中值滤波法及趋势面滤波法更易造成海底地形的失真,而本文方法的结果更加符合实际的海底趋势面。
4 结论与展望海洋测量受海洋环境的影响,在测深过程中易出现测深数据异常值。本文针对大面积异常值的检测与剔除,构建了条件变分自编码生成对抗网络模型,生成了与真实海底地形较为接近的海底趋势面。通过与中值滤波法及趋势面滤波法比较,本文提出的CVAE-GAN网络在大面积连续异常值的检测与剔除方面优于中值滤波法及趋势面滤波法,取得了较好的效果。但在碎石区的识别效果有待改进,因而本文方法更适合于海底地形特征明显的区域。同时,CVAE-GAN作为GAN的衍生模型,丰富了GAN模型在海洋测量数据处理领域的应用。
| [1] |
何义斌, 吴书帮, 谢洪燕, 等.
多波束异常测深数据检测方法实践[J]. 测绘科学, 2004, 29(1): 50–52.
HE Yibin, WU Shubang, XIE Hongyan, et al. Study of detection and filter of outlier on the sounding data of MES[J]. Science of Surveying and Mapping, 2004, 29(1): 50–52. |
| [2] |
翟国君, 黄谟涛.
海洋测量技术研究进展与展望[J]. 测绘学报, 2017, 46(10): 1752–1759.
ZHAI Guojun, HUANG Motao. The review of development of marine surveying technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1752–1759. DOI:10.11947/j.AGCS.2017.20170309 |
| [3] |
李家彪, 王小波, 华祖根, 等.
多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999: 197-207.
LI Jiabiao, WANG Xiaobo, HUA Zugen, et al. Principles and methods of multibeam surveying[M]. Beijing: China Ocean Press, 1999: 197-207. |
| [4] |
赵建虎, 刘经南.
多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008.
ZHAO Jianhu, LIU Jingnan. Multibeam echosounding and image data processing[M]. Wuhan: Wuhan University Press, 2008. |
| [5] |
刘雁春.
海洋测深空间结构及其数据处理[M]. 北京: 测绘出版社, 2003.
LIU Yanchun. Spatial structure of bathymetry and its data processing[M]. Beijing: Surveying and Mapping Press, 2003. |
| [6] | HERLIHY D R, STEPKA T N, RULON T D. Filtering erroneous soundings from multibeam survey data[J]. International Hydrographic Review, 1992, 69(2): 67–76. |
| [7] | WARE C. A system for cleaning high volume bathymetry[J]. International Hydrographic Review, 1992, 69(2): 77–94. |
| [8] | SHAW S, ARNOLD J. Automated error detection in multibeam bathymetry data[C]//Proceedings of the Ocean'93. Victoria, BC, Canada: IEEE, 1993(2): Ⅱ/89-Ⅱ/94. |
| [9] | EEG J. On the identification of spikes in soundings[J]. International Hydrographic Review, 2015, LXXⅡ(1): 33–41. |
| [10] | LIRAKIS C B, BONGIOVANNI K P. Automated multibeam data cleaning and target detection[C]//Proceedings of the Oceans 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings. Providence, RI, USA: IEEE, 2000: 719-723. |
| [11] | MANN M, AGATHOKLIS P, ANTONIOU A. Automatic outlier detection in multibeam data using median filtering[C]//Proceedings of 2001 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing. Victoria, BC, Canada: IEEE, 2001: 690-693. |
| [12] | CALDER B R, MAYER L A. Robust automatic multi-beam bathymetric processing[C]//Proceedings of the Center for Coastal and Ocean Mapping. Norfolk, VA, USA: Hydrographic Society of America, 2001. |
| [13] | JAKOBSSON M, CALDER B, MAYER L. On the effect of random errors in gridded bathymetric compilations[J]. Journal of Geophysical Research:Solid Earth, 2002, 107(B12): ETG 14-1–ETG 14-11. DOI:10.1029/2001JB000616 |
| [14] | CALDER B R, MAYER L A. Automatic processing of high-rate, high-density multibeam echosounder data[J]. Geochemistry, Geophysics, Geosystems, 2003, 4(6): 24–48. |
| [15] | GOODFELLOW I J, POUGETABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2014(3): 2672–2680. |
| [16] | GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge: The MIT Press, 2016. |
| [17] | RADFORD A, METZ L, CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv: 1511.06434, 2015. http://www.oalib.com/paper/4054347 |
| [18] | DENTON E, CHINTALA S, SZLAM A, et al. Deep generative image models using a laplacian pyramid of adversarial networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2015. |
| [19] | MIRZA M, OSINDERO S. Conditional generative adversarial nets[J]. arXiv preprint arXiv: 1411.1784, 2014. http://www.oalib.com/paper/4066323 |
| [20] |
李金洪, 黄永昌.
深度学习之TensorFlow入门、原理与进阶实战[M]. 北京: 机械工业出版社, 2018.
LI Jinhong, HUANG Yongchang. Getting started and best practices with tensorFlow for deep learning[M]. Beijing: China Machine Press, 2018. |
| [21] | WELLING M, ROSEN-ZVI M, HINTON G E. Exponential family harmoniums with an application to information retrieval[C]//Proceedings of the 17th International Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada: MIT Press, 2004. |
| [22] | VINCENT P. A connection between score matching and denoising autoencoders[J]. Neural Computation, 2011, 23(7): 1661–1674. DOI:10.1162/NECO_a_00142 |
| [23] | DUCHI J, HAZAN E, SINGER Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011(12): 2121–2159. |



