2. 国家海洋局海底科学重点实验室, 浙江 杭州 310012;
3. 上海交通大学海洋研究院, 上海 200030
2. Key Laboratory of Submarine Geosciences, State Oceanic Administration, Hangzhou 310012, China;
3. Institute of Oceanography, Shanghai Jiao Tong University, Shanghai 200030, China
精确可靠的水深数据几乎是从事一切海洋活动的基础[1],高分辨率的数字水深模型(digital bathymetric model,DBM)不仅可用于海图的构建,还可用于地貌特征与成因[2-3]、海底构造、海洋资源、水动力流体模型、生物栖息地与生态系统等多个方面的研究[4-14]。对海洋测深的系统研究持续了一个多世纪[15-19],从早期极低效率的锤线测深发展到当前高精度、高分辨率、高效率的多波束测深技术[20-22]。然而,由于全球海洋极其广阔,基于船载模式的多波束测深成本高昂[23],导致目前仍有超过80%的全球海域未被多波束探测[24]。因此,在构建深海大范围DBM时仍需使用历史测深资料[25]。当前大洋测深数据主要针对不同目的独立采集,导致来源、格式和分辨率等方面存在诸多差异[26-28]。全球大洋测深数据的多源复杂性,不利于高精度DBM的构建,更不利于日益迫切认识海洋、经略海洋的国家战略需求。
DBM的构建也称数据的网格化。网格化是二维采样、插值和二维外推的结合[29]。如何基于插值算法将多源水深数据融合进而构建DBM一直是学者们的研究热点。根据目前国内外对多源水深数据融合技术的研究,融合方法主要是基于克里金、双三次样条、张力样条等插值算法进行综合应用,如文献[30]将多波束、单波束、历史海图等水深数据进行融合,编制了北冰洋的国际海底地形图(international bathymetric chart of the arctic ocean,IBCAO);文献[31]根据多种水深数据汇编了南大洋的国际海底地形图(international bathymetric chart of the southern ocean,IBCSO);文献[32]结合不同时期的多波束、单波束和海岸线等数据,构建了南极洲东部George V大陆边缘的DBM,得到该区较详尽的海底地貌信息。上述方法虽实现了多源水深数据的融合,但融合后的数据空间分辨率低(>500 m),且难以保证数据稀疏区和空白区的插值精度。因此,在保证数据稀疏区插值精度的同时,既要提高数据空白区的精度,又要保留高分辨率水深源数据的细节特征,是值得深入研究的科学技术问题。
为解决上述问题,本文提出合并-融合(merge-fusion,MF)法。该方法将多波束、单波束、电子海图数据与通用全球海洋地形(general bathymetric chart of the oceans,GEBCO)数据融合,在保留高分辨率地形细节特征的同时,合理填补了数据空白区,形成“挑战者深渊”分辨率100 m的高精度DBM。结果表明,该方法融合的DBM能更好地反映精细的地形特征信息,为区域性或全球性DBM的构建以及多源异构水深数据的管理利用提供了实用化技术方案。
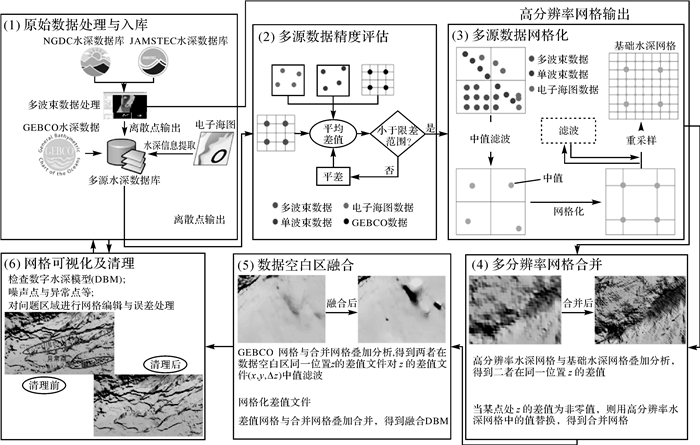
1 MF方法基本原理与步骤MF(merge-fusion)法的核心思想为“合并-融合”。如图 1所示,该方法主要包括6个步骤:
|
| 图 1 MF方法原理及流程 Fig. 1 Principle and workflow of the MF method |
(1) 原始数据处理与入库。根据不同水深数据的来源、类型,对其进行精细处理。以多波束数据为例,对于系统误差,通过潮位改正、声速剖面改正、换能器安装偏差校准等方法进行消除[33-39];对于异常值,通过人工或者自动滤波算法识别并剔除[20];而随机误差,只能通过对测深数据的精度评估评价其误差大小[40]。建立多源水深数据库,对清理后的水深数据进行统一管理。
(2) 多源数据精度评估。对多源水深数据进行精度评估是保证成果网格数据质量的重要手段[40]。在同一水域,以多波束条带数据的中央波束测深结果为基准,使用平均差值式[30](1)对多源数据进行精度评估
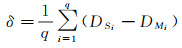 (1)
(1)
式中,δ为平均水深差;q为测深数据个数;DMi为多波束水深数据;DSi为多源水深数据,水深值取负值。
根据《GB 12327—1998海道测量规范》,将水深偏差与水深的2%比较,若偏差小于水深的2%,符合规范要求不做处理;否则根据偏差值以多波束条带数据的中央波束测深结果为基准,对其他类型数据进行最小二乘法平差处理[28, 41]。通过式(2)来表示误差效应
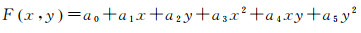 (2)
(2)
式中,(x, y)为测点坐标;a0, a1, a2, a3, a4, a5为待定系数。
设水深观测值Z的改正数为V,以多波束条带数据的中央波束测深结果为基准,建立如下误差方程
 (3)
(3)
式中,VSi、VMi分别为多源数据和多波束数据在点i位置(x, y)处的改正数;ZSi,ZMi分别为相应位置处的多源数据和多波束数据水深值。
根据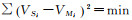
(3) 多源数据网格化。为避免网格内潜在异常值的影响[42],对多源水深数据库导出的离散水深点进行中值滤波。中值滤波首先确定奇数像元网格G,网格内各像元按数值大小排序,并将网格节点内的中值水深d(x, y)作为原数值s(x, y)[43]
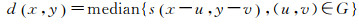 (4)
(4)
为保证数据稀疏区域插值的准确性[44],对滤波后的多源水深数据进行网格化[45-47],形成低分辨率网格。地球科学领域最常见的网格化方法之一是双三次样条插值算法[48],该算法可通过已知点精确插值,得到光滑的插值曲面,但在地形突变处或数据稀疏区易产生异常值,掩盖真实地形。本文采用目前国际上普遍使用的连续曲率张力样条插值算法[48-49]对多源数据进行网格化,该算法由于引入张力因子,可消除最小曲率拟合面中存在的较大波动和无关变形点[43],网格化后的结果更加平滑、准确。该算法基于最小曲率拟合面原则
 (5)
(5)
式中,(xi, yi, zi)为已知点坐标;N为已知点个数;fi为点(xi, yi)处格林函数线性组合解中的系数;δ(x-xi, y-yi)为给定响应函数;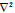
边界条件为
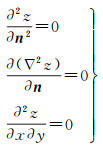 (6)
(6)
式中,n为曲面法线方向的单位向量;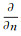
在此基础上,引入张力因子T,得到
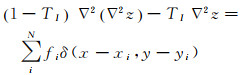 (7)
(7)
式中,TI为拟合面内部张力因子,在[0, 1)区间内取值。
边界条件为
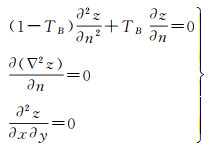 (8)
(8)
式中,TB为拟合面边界处张力因子,在[0, 1)区间内取值。
当张力因子T=0时,式(7)简化为式(5),此时无张力,得到最小曲率平滑解;T=1时,张力最大,得到调和样条解。对于大洋水深数据,张力因子一般选取0.32~0.4之间[30]。随后对低分辨率网格滤波,将滤波后的低分辨率网格重采样至目标分辨率,得到“基础水深网格”。
(4) 多分辨率网格合并。为合并多分辨率网格,且保留高精度测深区域地形细节特征,使用高分辨率网格水深值替换低分辨率网格水深值。首先,将预处理步骤中输出的高分辨率网格与基础水深网格叠加分析,得到二者在同一位置处z的差值;对z的差值进行判断,若差值非零则用多波束数据网格点内相应值进行替换,得到“合并水深网格”。
为消除网格合并过程出现的边缘效应[50],在高分辨率网格数据一侧定义过渡带,过渡带宽度至少为3列网格点,具体范围根据接边情况来确定。其原理基于双曲线加权函数
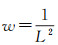 (9)
(9)
式中,L代表到下一高分辨率数据约束单元或过渡带外约束单元的距离;w表示权重[31]。
由式(9)可看出,距离高分辨率数据网格单元越近,受深度影响越小,由此弱化边缘效应发生的概率。
(5) 数据空白区融合。在数据空白区域范围内,将GEBCO网格与合并水深网格“作差”,即GEBCO网格内每个数据点减去相同位置处插值数据点的值,得到包含经度、纬度和水深差异的差值文件。随后网格化中值滤波后的差值文件,得到差值网格。将差值网格叠加整合到合并水深网格,得到融合后的DBM。
(6) 网格可视化及清理。经上述步骤得到的DBM难免存在各种“毛刺”等异常点,使用三维地形浏览法找出这些问题。为突出数据噪声,可使用光照效果加以突出,最后通过曲面拟合算法[51]对网格问题区域进行编辑和误差处理,以获得最佳的数字水深模型。曲面拟合算法的构建原理:根据波束点拟合海底趋势面,计算实测水深数据与趋势面间的深度差值,结合误差处理理论剔除异常点[52]。曲面拟合法中拟合函数的一般形式
 (10)
(10)
式中,Ψ(x, y)为曲面拟合函数;(x, y, z)为波束点空间坐标;hlm为多项式系数;k为多项式总阶数;(xc, yc, zc)为待检测点c;Q(xc, yc, zc)为以c为中心的曲面拟合函数的局部曲面拟合范围。
2 数据来源位于马里亚纳海沟南端的“挑战者深渊”是全球海洋最深处,被誉为“世界第四极”,一直以来都是全球海洋科学研究的热点区域[53-56]。近几年来,我国在该区域组织了数次综合海洋调查。高精度的海沟区DBM是开展载人深潜、海底原位观测和板块俯冲数值模拟[57]的基础,但该区现有数据分辨率低、精度差,难以满足海洋科学研究和工程实施要求。同时,该海区数据来源多样,且存在诸多数据空白区,适合数据融合技术的方法研究。
本文数据主要来自于公开的海洋数据,包括多波束数据、单波束数据、电子海图数据以及GEBCO数据。
2.1 多波束数据构建此次DBM的核心数据主要是多波束数据,采集自2003年以后,且精度较高。在该区域共收集25个航次的多波束数据,其中,15个调查航次数据源于美国大气与海洋局(NOAA)下属的国家地质与地球物理数据中心(NGDC),另外10个多波束测深航次数据则从日本海洋-地球科学和技术研究中心(JAMSTEC)获得。
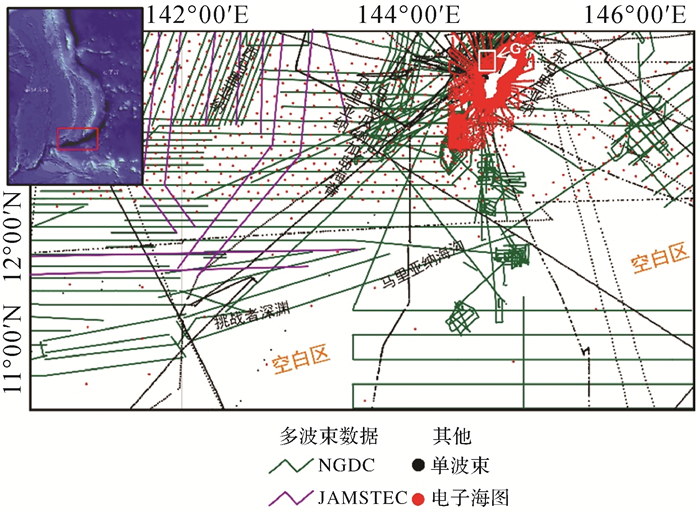
2.2 单波束数据除多波束数据外,还从NGDC收集了2000年以来的大量单波束测深点数据(图 2)。由于收集的单波束数据未提供测深仪及定位系统等相关详细信息,很难对所有数据进行精度评估。且单波束测深点空间分布非常不均匀,只在使用多波束探测区域分布较为密集,例如美国关岛附近。
|
| G区为多源数据精度评定所选区 图 2 “挑战者深渊”位置和数据源 Fig. 2 Location and data sources of the "Challenger Deep" |
2.3 电子海图数据
从美国国家海洋和大气管理局(NOAA)下的海岸调查部门(Office of Coast Survey)共收集该区域2005年来的4幅电子海图数据。除电子海图数据外无相关元数据信息,因此无法全面评估其数据精度。
2.4 GEBCO数据虽然已有大量水深数据,但仍存在范围达上千平方公里的数据空白区,本文使用GEBCO_2014[58]水深数据集对数据空白区进行填补。GEBCO数据是当前国际主流水深数据集之一,而GEBCO_2014为目前全球测深数据集的最新版本,主要源于实测数据和利用卫星高度计反演的预测水深,网格分辨率为30″。
3 MF方法的实现根据上述方法对实验区多源水深数据进行融合处理,构建马里亚纳海沟“挑战者深渊”的DBM。首先将多源水深数据处理为离散数据格式,转换水平坐标,投影方式和深度基准面分别统一至UTM投影和平均海平面。随后进行系统误差处理,并使用CUBE算法清理多源水深数据的异常点[59-60],后重新导出为离散格式,形成“挑战者深渊”的多源水深数据库。
为对多源水深数据进行精度评定,比较了美国关岛西北部区域(图 2区域G)内多源水深数据的深度差异。该区域被多波束数据全覆盖,精度较高,适合用于精度评估。离散的电子海图和单波束水深点分别与分辨率100 m的多波束条带数据的中央波束测深结果进行比较(图 3)。两者分别与多波束进行一一组合,组合的准则是二者间距小于50 m[30]。选取115对电子海图水深对比数据、207对单波束水深对比数据,依据式(1)得到对比结果,分别见表 1和图 3。

|
| 蓝色点代表电子海图数据,红色点代表单波束数据,直方图表示深度差值绝对值分布 图 3 电子海图、单波束与多波束数据水深值对比 Fig. 3 Comparison of water depth of electronic charts, single-beam and multi-beam bathymetric data |
| m | |||
| 对象 | 平均差值 | 平均水深 | ±2%·水深 |
| 电子海图vs多波束 | -18.9 | -1039 | ±20.7 |
| 单波束vs多波束 | -23.2 | -1278 | ±25.5 |
| GEBCO_2014 vs多波束 | -10.7 | -1185 | ±23.7 |
根据《GB 12327—1998海道测量规范》,对于电子海图数据,平均水深1039 m时,平均水深差值优于水深值的2%;对于单波束数据,平均水深1278 m时,平均水深差值同样优于水深的2%。经过评定,单波束数据、电子海图数据精度在限差容许范围内,可作为本次数据融合实验的数据集。
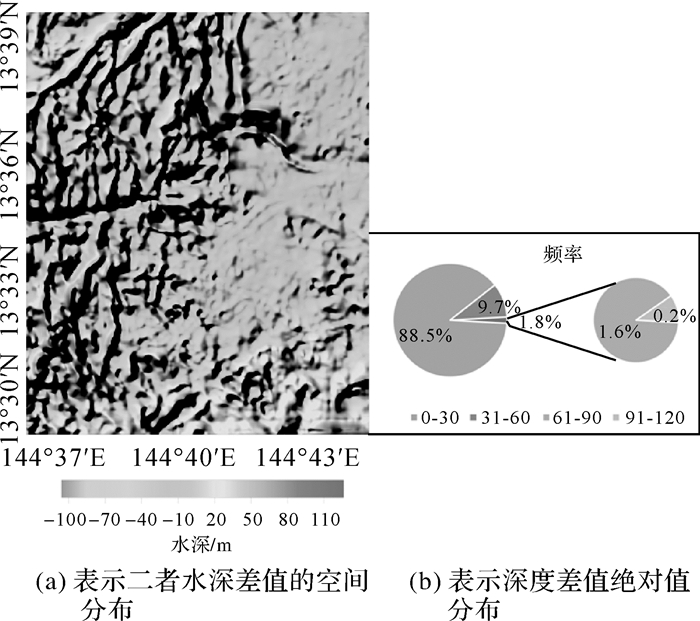
以区域G内多波束条带数据的中央波束测深结果为基准,对GEBCO_2014数据进行精度评估。在分辨率100 m基础上,得到二者水深差值的空间位置分布(图 4)。应用式(1)从29605对GEBCO对比数据中,得到对比结果,分别见表 1和饼状图(图 4)。平均水深1185 m时,平均深度差优于水深的2%。GEBCO_2014数据精度同样在限差容许范围内,可作为本次数据空白区融合实验的数据集。
|
| 图 4 GEBCO_2014数据与多波束数据水深值对比 Fig. 4 Comparison of water depth of GEBCO_2014 data and multi-beam bathymetric data |
对多源水深数据(图 5(a))进行网格大小1000 m的中值滤波。随后网格化滤波后的水深数据,形成分辨率1000 m的低分辨率水深网格(图 5(b))。对低分辨率网格进行平滑和滤波,将滤波后的低分辨率网格重采样至100 m作为“基础水深网格”(图 5(c))。

|
| 图 5 多源数据融合过程示例 Fig. 5 An example of multi-source data fusion |
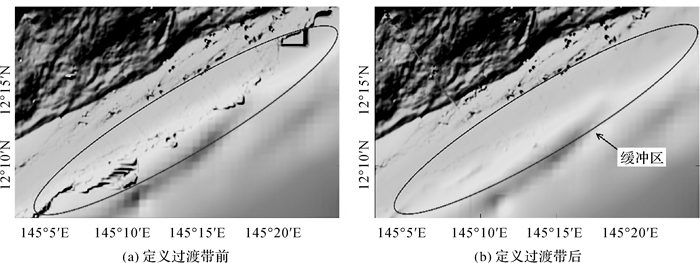
通过对多波束数据进行处理,例如声速剖面改正、异常值剔除等测深条带拼接步骤[33, 43, 61-63]得到分辨率100 m的高分辨水深网格(图 5(d))。然后将高分辨率水深网格与基础水深网格叠加分析,得到二者在同一位置处z的差值。若某点处z的差值非零,则用高分辨率水深网格内相应水深值替换,得到“合并水深网格”(图 5(e))。为消除多分辨率网格间的边缘效应,在靠近高分辨率网格数据边界定义5 km的过渡带(图 6),极大地降低了边缘效应产生的概率。
|
| 图 6 过渡带定义前后对比 Fig. 6 Comparison of the DBM |
结合GEBCO_2014数据,对数据空白区域进行融合。首先将GEBCO_2014网格与合并水深格网叠加合并,得到数据空白范围内同一位置处的水深差值文件,差值文件包括经度、纬度和深度差值信息。随后对差值文件进行网格大小1000 m的中值滤波。将滤波后的差值文件网格化为分辨率100 m的差值网格。最后,将差值网格与合并水深网格叠加整合,得到融合后的DBM(图 5(f))。
可视化浏览合并-融合后的水深网格,识别并高亮异常点,对网格问题区域进行编辑和误差处理,最终得到满意的DBM。
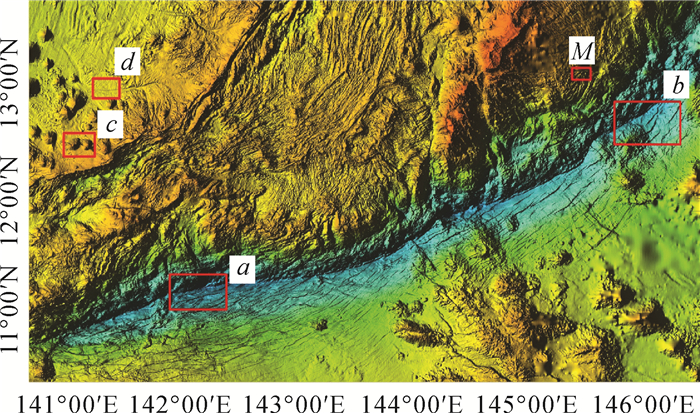
4 分析与讨论 4.1 数据拼接对比图 7为使用MF法得到的马里亚纳海沟“挑战者深渊”DBM,网格分辨率100 m。经统计,本次所选区域多波束、单波束和电子海图数据的覆盖率分别为42.2%、0.5%、0.2%,使用GEBCO数据对剩余57%的数据空白区进行填补。通过网格可看出,MF方法不仅保留了高分辨率数据区详细的海底特征,还为数据稀疏区和空白区提供了平滑的地形表面。
|
| M为数据拼接对比区;a、b、c、d为数据细节对比区 图 7 “挑战者深渊”DBM Fig. 7 The DBM of the "Challenger Deep" |
在马里亚纳海沟“挑战者深渊”地区,除本文构建的“挑战者深渊”DBM之外,只有全球数据集涵盖整个大洋。本文将“挑战者深渊”DBM与GEBCO_2014DBM进行比较。结果表明,在数据接边处,MF法取得较为理想的效果,接边处总体限差符合《GB 12327—1998海道测量规范》,即水深大于100 m时,深度测量的极限误差应优于水深的2%。在实验区选取接边差异较大区域M(图 7),针对MF法和传统方法得到剖面a-a′(图 8(a))和剖面b-b′(图 8(b))。从剖面图可看出,两种方法形成差异主要集中在距剖面线起点2~4 km范围内区域。以剖面线起点为原点,剖面方向为正方向,选取(2.6 km,2.8 km)范围内剖面A和B(图 8),在水深约3600 m处,水深限差50 m时,对于传统方法,平均坡度为72.32°(图 8(b));而MF法,平均坡度为37.63°,与前者相比整体过渡较为平缓(图 8(a))。

|
| 图 8 数据接边处比较 Fig. 8 Comparison of data transition area |
4.2 数据细节对比
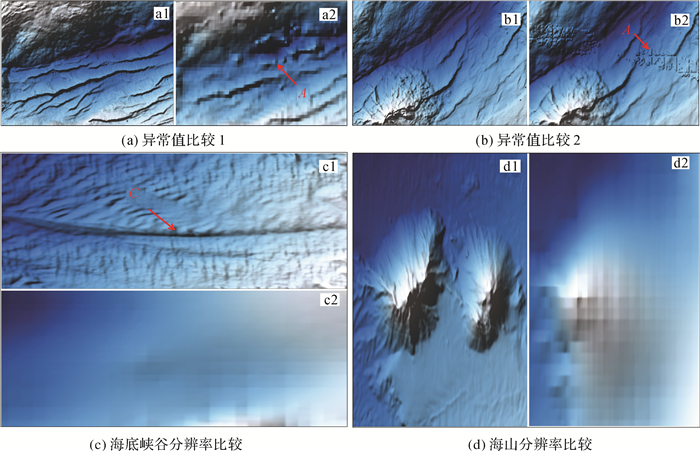
高分辨率水深数据结合越多,网格分辨率就会越高,这使得本次融合的分辨率100 m的“挑战者深渊”DBM成为该区域目前精度最高的数据集;同时,该数据集对“挑战者深渊”地区的地形细节特征刻画有着显著改善。例如,在网格单元100 m的“挑战者深渊”DBM中,可清晰地看到海底峡谷等地形特征(图 9(d)),以及形态、轮廓更明显的海山(图 9(c)),而在GEBCO_2014数据集中几乎看不到此类地形特征。在数据稀疏区,利用清理过的单波束或电子海图数据形成的低分辨率网格避免了异常点的出现(图 9(a)和9(b))。但仍存在数据密度和质量较差地区,这些区域包含潜在异常点、噪声点,需进一步调查才能识别和处理。
|
| a1、b1、c1、d1为MF法所得DBM,a2、b2、c2、d2为传统方法所得DBM,A代表异常点,C代表海底峡谷 图 9 “挑战者深渊”DBM与GEBCO_2014DBM细节对比 Fig. 9 Comparison of data details between "Challenger Deep" DBM and GEBCO_2014 DBM |
5 结论
(1) 提出并实现了一种适用于多源水深数据融合的MF方法,并给出详细的融合技术方法流程。其基本原理是基于多源水深数据形成两种分辨率网格,然后将多分辨率网格合并,在此基础上使用GEBCO数据进行融合,叠加、合并得到最终的DBM。
(2) 基于马里亚纳海沟“挑战者深渊”地区公开的多波束、单波束、电子海图等水深数据,采用MF多源数据融合方法,构建了“挑战者深渊”的高精度DBM,验证了本文方法的可靠性和实用价值。
(3) 针对同一区域,利用本文方法得到的DBM与目前国际主流的GEBCO_2014数据集进行对比,表明本文方法更能够体现高分辨率水深数据和数据空白区的细节信息、防止边缘效应和异常点的产生,从而获得高精度的海底DBM。
| [1] |
吴自银, 阳凡林, 李守军, 等.
高分辨率海底地形地貌——可视计算与科学应用[M]. 北京: 科学出版社, 2017.
WU Ziyin, YANG Fanlin, LI Shoujun, et al. High resolution submarine geomorphology[M]. Beijing: Science Press, 2017. |
| [2] | WU Ziyin, LI Jiabiao, JIN Xianglong, et al. Distribution, features, and influence factors of the submarine topographic boundaries of the okinawa trough[J]. Science China Earth Sciences, 2014, 57(8): 1885–1896. DOI:10.1007/s11430-013-4810-3 |
| [3] | WU Ziyin, JIN Xianglong, ZHOU Jieqiong, et al. Comparison of buried sand ridges and regressive sand ridges on the outer shelf of the east China sea[J]. Marine Geophysical Research, 2017, 38(1-2): 187–198. DOI:10.1007/s11001-016-9278-z |
| [4] | SMITH W H F, SANDWELL D T. Global sea floor topography from satellite altimetry and ship depth soundings[J]. Science, 1997, 277(5334): 1956–1962. DOI:10.1126/science.277.5334.1956 |
| [5] |
赵建虎.
现代海洋测绘[M]. 武汉: 武汉大学出版社, 2008.
ZHAO Jianhu. Modern marine surveying and charting[M]. Wuhan: Wuhan University Press, 2008. |
| [6] |
赵建虎, 欧阳永忠, 王爱学.
海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1786–1794.
ZHAO Jianhu, OUYANG Yongzhong, WANG Aixue. Status and development tendency for seafloor terrain measurement technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1786–1794. DOI:10.11947/j.AGCS.2017.20170276 |
| [7] |
刘经南, 赵建虎.
多波束测深系统的现状和发展趋势[J]. 海洋测绘, 2002, 22(5): 3–6.
LIU Jingnan, ZHAO Jianhu. The present status and developing trend of the multibeam system[J]. Hydrographic Surveying and Charting, 2002, 22(5): 3–6. DOI:10.3969/j.issn.1671-3044.2002.05.001 |
| [8] |
陆秀平, 黄谟涛, 翟国君, 等.
多波束测深数据处理关键技术研究进展与展望[J]. 海洋测绘, 2016, 36(4): 1–6, 11.
LU Xiuping, HUANG Motao, ZHAI Guojun, et al. Development and prospect of key technologies for multibeam echosounding data processing[J]. Hydrographic Surveying and Charting, 2016, 36(4): 1–6, 11. DOI:10.3969/j.issn.1671-3044.2016.04.001 |
| [9] |
赵建虎, 王爱学.
精密海洋测量与数据处理技术及其应用进展[J]. 海洋测绘, 2015, 35(6): 1–7.
ZHAO Jianhu, WANG Aixue. Precise marine surveying and data processing technology and their progress of application[J]. Hydrographic Surveying and Charting, 2015, 35(6): 1–7. DOI:10.3969/j.issn.1671-3044.2015.06.001 |
| [10] | MVLLER R D, QIN Xiaodong, SANDWELL D T, et al. The GPlates Portal:Cloud-based interactive 3D visualization of global geophysical and geological data in a web browser[J]. PLoS One, 2016, 11(3): e0150883. DOI:10.1371/journal.pone.0150883 |
| [11] | BOLMER S T, BEARDSLEY R C, PUDSEY C, et al. A high-resolution bathymetry map for the marguerite bay and adjacent west antarctic peninsula shelf for the southern ocean GLOBEC program[R].[S.l.]: Woods Hole Oceanographic Institution, 2004: 2603-2639. |
| [12] | ZHOU Jieqiong, WU Ziyin, JIN Xianglong, et al. Observations and analysis of giant sand wave fields on the Taiwan banks, northern South China Sea[J]. Marine Geology, 2018, 406: 132–141. DOI:10.1016/j.margeo.2018.09.015 |
| [13] |
金绍华, 李家彪, 吴自银, 等.
海底底质分类反向散射强度三维概率密度法[J]. 测绘学报, 2019, 48(1): 124–131.
JIN Shaohua, LI Jiabiao, WU Ziyin, et al. 3D histogram of backscatter strength for seafloor substrates classification[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 124–131. DOI:10.11947/j.AGCS.2019.20170631 |
| [14] | WANG Mingwei, WU Ziyin, YANG Fanlin, et al. Multifeature extraction and seafloor classification combining LiDAR and MBES data around yuanzhi island in the south China sea[J]. Sensors, 2018, 18(11): 3828. DOI:10.3390/s18113828 |
| [15] | DANIELSON J J, GESCH D B. Global multi-resolution terrain elevation data 2010(GMTED2010)[R]. Reston, Virginia: U.S. Geological Survey, 2011. |
| [16] | JAKOBSSON M, CALDER B, MAYER L. On the effect of random errors in gridded bathymetric compilations[J]. Journal of Geophysical Research:Solid Earth, 2002, 107(B12): 2358. |
| [17] |
李家彪.
多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999.
LI Jiabiao. Multibeam sounding principles, survey technologies and data processing methods[M]. Beijing: Ocean Press, 1999. |
| [18] | HALL J K. Digital topography and bathymetry of the area of the dead sea depression[J]. Tectonophysics, 1996, 266(1-4): 177–185. DOI:10.1016/S0040-1951(96)00189-8 |
| [19] | HALL J K. GEBCO centennial special issue-charting the secret world of the ocean floor:The GEBCO project 1903-2003[J]. Marine Geophysical Researches, 2006, 27(1): 1–5. DOI:10.1007/s11001-006-8181-4 |
| [20] |
吴自银, 阳凡林, 罗孝文, 等.
高分辨率海底地形地貌——探测处理理论与技术[M]. 北京: 科学出版社, 2017.
WU Ziyin, YANG Fanlin, LUO Xiaowen, et al. High resolution submarine geomorphology[M]. Beijing: Science Press, 2017. |
| [21] |
赵建虎.多波束深度及图像数据处理方法研究[D].武汉: 武汉大学, 2002. ZHAO Jianhu. Research on multibeam depth and image processing methods[D]. Wuhan: Wuhan University, 2002. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y557919 |
| [22] |
阳凡林, 李家彪, 吴自银, 等.
浅水多波束勘测数据精细处理方法[J]. 测绘学报, 2008, 37(4): 444–450, 457.
YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The methods of high quality post-processing for shallow multibeam data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 444–450, 457. DOI:10.3321/j.issn:1001-1595.2008.04.008 |
| [23] | VOGT P R, JUNG W Y. GOMaP:A matchless resolution to start the new millennium[J]. Eos, Transactions American Geophysical Union, 2000, 81(23): 254–258. |
| [24] | MAYER L, JAKOBSSON M, ALLEN G, et al. The Nippon foundation-GEBCO seabed 2030 project:the quest to see the world's oceans completely mapped by 2030[J]. Geosciences, 2018, 8(2): 63. DOI:10.3390/geosciences8020063 |
| [25] | BECKER J J, SANDWELL D T, SMITH W H F, et al. Global bathymetry and elevation data at 30 arc seconds resolution:SRTM30_PLUS[J]. Marine Geodesy, 2009, 32(4): 355–371. DOI:10.1080/01490410903297766 |
| [26] |
赵建虎, 王爱学, 郭军.
多波束与侧扫声呐图像区块信息融合方法研究[J]. 武汉大学学报(信息科学版), 2013, 38(3): 287–290.
ZHAO Jianhu, WANG Aixue, GUO Jun. Study on fusion method of the block image of MBS and SSS[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 287–290. |
| [27] |
阳凡林, 吴自银, 独知行, 等.
多波束声纳和侧扫声纳数字信息的配准及融合[J]. 武汉大学学报(信息科学版), 2006, 31(8): 740–743.
YANG Fanlin, WU Ziyin, DU Zhixing, et al. Co-registering and fusion of digital information of multi-beam sonar and side-scan sonar[J]. Geomatics and Information Science of Wuhan University, 2006, 31(8): 740–743. |
| [28] |
黄谟涛, 翟国君, 欧阳永忠, 等.
多波束与单波束测深数据的融合处理技术[J]. 测绘学报, 2001, 30(4): 299–303.
HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. Data fusion technique for single beam and multibeam echosoundings[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 299–303. DOI:10.3321/j.issn:1001-1595.2001.04.005 |
| [29] | TOBLER W R. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46(S1): 234–240. |
| [30] | JAKOBSSON M, MAYER L, COAKLEY B, et al. The international bathymetric chart of the Arctic Ocean (IBCAO) version 3.0[J]. Geophysical Research Letters, 2012, 39(12): L12609. |
| [31] | ARNDT J E, SCHENKE H W, JAKOBSSON M, et al. The international bathymetric chart of the Southern Ocean (IBCSO) version 1.0-A new bathymetric compilation covering Circum-Antarctic waters[J]. Geophysical Research Letters, 2013, 40(12): 3111–3117. DOI:10.1002/grl.50413 |
| [32] | BEAMAN R J, O'BRIEN P E, POST A L, et al. A new high-resolution bathymetry model for the Terre adélie and George V continental margin, East Antarctica[J]. Antarctic Science, 2011, 23(1): 95–103. DOI:10.1017/S095410201000074X |
| [33] |
赵建虎, 刘经南.
精密多波束测深系统位置修正方法研究[J]. 武汉大学学报(信息科学版), 2002, 27(5): 473–477.
ZHAO Jianhu, LIU Jingnan. Development of method in precise multibeam acoustic bathymetry[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5): 473–477. |
| [34] | ZHAO Jianhu, MENG Junxia, ZHANG Hongmei, et al. A new method for acquisition of high-resolution seabed topography by matching seabed classification images[J]. Remote Sensing, 2017, 9(12): 1214. DOI:10.3390/rs9121214 |
| [35] | WU Ziyin, LI Jiabiao, LI Shoujun, et al. A new method to identify the foot of continental slope based on an integrated profile analysis[J]. Marine Geophysical Research, 2017, 38(1-2): 199–207. DOI:10.1007/s11001-016-9273-4 |
| [36] |
阳凡林, 李家彪, 吴自银, 等.
多波束测深瞬时姿态误差的改正方法[J]. 测绘学报, 2009, 38(5): 450–456.
YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The methods of removing instantaneous attitude errors for multibeam bathymetry data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 450–456. DOI:10.3321/j.issn:1001-1595.2009.05.012 |
| [37] |
吴自银, 李家彪.
多波束勘测的数据编辑方法[J]. 海洋通报, 2000, 19(3): 74–78.
WU Ziyin, LI Jiabiao. The editing methods of multi-beam survey data[J]. Marine Science Bulletin, 2000, 19(3): 74–78. DOI:10.3969/j.issn.1001-6392.2000.03.013 |
| [38] |
吴自银, 李家彪, 阳凡林, 等.
一种大陆坡脚点自动识别与综合判断方法[J]. 测绘学报, 2014, 43(2): 170–177.
WU Ziyin, LI Jiabiao, YANG Fanlin, et al. An intergrated method for automatic identification of the foot point of slope[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 170–177. DOI:10.13485/j.cnki.11-2089.2014.0025 |
| [39] |
赵荻能, 吴自银, 周洁琼, 等.
声速剖面精简运算的改进D-P算法及其评估[J]. 测绘学报, 2014, 43(7): 681–689.
ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. A method for streamlining and assessing sound velocity profiles based on improved D-P algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 681–689. DOI:10.13485/j.cnki.11-2089.2014.0132 |
| [40] |
张国堙, 陶春辉, 王奡, 等.
深水多波束声呐测深数据精度评估[J]. 海洋学报, 2017, 39(11): 106–114.
ZHANG Guoyin, TAO Chunhui, WANG Ao, et al. Accuracy evaluation of multibeam echo sounder bathymetry data[J]. Acta Oceanologica Sinica, 2017, 39(11): 106–114. DOI:10.3969/j.issn.0253-4193.2017.11.010 |
| [41] |
朱庆, 李德仁.
多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 23(1): 1–4, 46.
ZHU Qing, LI Deren. Error analysis and processing of multibeam soundings[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 1–4, 46. DOI:10.3321/j.issn:1671-8860.1998.01.001 |
| [42] |
樊妙, 孙毅, 邢喆, 等.
基于多源水深数据融合的海底高精度地形重建[J]. 海洋学报, 2017, 39(1): 130–137.
FAN Miao, SUN Yi, XING Zhe, et al. Bathymetry fusion techniques for high-resolution digital bathymetric modeling[J]. Acta Oceanologica Sinica, 2017, 39(1): 130–137. DOI:10.3969/j.issn.0253-4193.2017.01.014 |
| [43] |
阳凡林, 刘经南, 赵建虎.
多波束测深数据的异常检测和滤波[J]. 武汉大学学报(信息科学版), 2004, 29(1): 80–83.
YANG Fanlin, LIU Jingnan, ZHAO Jianhu. Detecting outliers and filtering noises in multi-beam data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1): 80–83. |
| [44] | HELL B, JAKOBSSON M. Gridding heterogeneous bathymetric data sets with stacked continuous curvature splines in tension[J]. Marine Geophysical Research, 2011, 32(4): 493–501. DOI:10.1007/s11001-011-9141-1 |
| [45] |
贾帅东, 张立华, 宋国大, 等.
基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454–460.
JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A method for constructing an adaptive grid digital depth model based on mean vertical uncertainty of area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 454–460. |
| [46] |
张立华, 贾帅东, 吴超, 等.
顾及不确定度的数字水深模型内插方法[J]. 测绘学报, 2011, 40(3): 359–365.
ZHANG Lihua, JIA Shuaidong, WU Chao, et al. A method for interpolating digital depth model considering uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 359–365. |
| [47] |
贾帅东, 张立华, 彭认灿, 等.
基于多波束数据的网格水深模型内插方法精度分析[J]. 海洋测绘, 2013, 33(5): 24–26, 37.
JIA Shuaidong, ZHANG Lihua, PENG Rencan, et al. The accuracy analysis for grid depth model interpolations based on multibeam echosounder data[J]. Hydrographic Surveying and Charting, 2013, 33(5): 24–26, 37. DOI:10.3969/j.issn.1671-3044.2013.05.006 |
| [48] | BRIGGS I C. Machine contouring using minimum curvature[J]. Geophysics, 1974, 39(1): 39–48. |
| [49] | SMITH W H F, WESSEL P. Gridding with continuous curvature splines in tension[J]. Geophysics, 1990, 55(3): 293–305. DOI:10.1190/1.1442837 |
| [50] | ZHAO Jianhu, YAN Jun, ZHANG Hongmei, et al. A new method for weakening the combined effect of residual errors on multibeam bathymetric data[J]. Marine Geophysical Research, 2014, 35(4): 379–394. DOI:10.1007/s11001-014-9228-6 |
| [51] |
吴自银, 金翔龙, 郑玉龙, 等.
多波束测深边缘波束误差的综合校正[J]. 海洋学报, 2005, 27(4): 88–94.
WU Ziyin, JIN Xianglong, ZHENG Yulong, et al. Integrated error correction of multi-beam marginal sounding beam[J]. Acta Oceanologica Sinica, 2005, 27(4): 88–94. DOI:10.3321/j.issn:0253-4193.2005.04.012 |
| [52] |
张志衡, 彭认灿, 黄文骞, 等.
考虑自然邻点影响域的多波束测深数据趋势面滤波改进算法[J]. 测绘学报, 2018, 47(1): 35–47.
ZHANG Zhiheng, PENG Rencan, HUANG Wenqian, et al. An improved algorithm of tendency surface filtering in multi-beam bathymetric data considering the natural neighboring points influence field[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 35–47. DOI:10.11947/j.AGCS.2018.20160565 |
| [53] | FRYER P, BECKER N, APPELGATE B, et al. Why is the challenger deep so deep?[J]. Earth and Planetary Science Letters, 2003, 211(3-4): 259–269. DOI:10.1016/S0012-821X(03)00202-4 |
| [54] | NAKANISHI M, HASHIMOTO J. A precise bathymetric map of the world's deepest seafloor, challenger deep in the Mariana trench[J]. Marine Geophysical Research, 2011, 32(4): 455–463. DOI:10.1007/s11001-011-9134-0 |
| [55] | STERN R, SMOOT N C. A bathymetric overview of the Mariana forearc[J]. Island Arc, 1998, 7(3): 525–540. DOI:10.1111/j.1440-1738.1998.00208.x |
| [56] | GARDNER J V, ARMSTRONG A A, CALDER B R, et al. So, how deep is the Mariana trench?[J]. Marine Geodesy, 2014, 37(1): 1–13. DOI:10.1080/01490419.2013.837849 |
| [57] | ZHOU Zhiyuan, LIN Jian, BEHN M D, et al. Mechanism for normal faulting in the subducting plate at the Mariana trench[J]. Geophysical Research Letters, 2015, 42(11): 4309–4317. DOI:10.1002/2015GL063917 |
| [58] | WEATHERALL P, MARKS K M, JAKOBSSON M, et al. A new digital bathymetric model of the world's oceans[J]. Earth and Space Science, 2015, 2(8): 331–345. DOI:10.1002/2015EA000107 |
| [59] |
黄谟涛, 翟国君, 柴洪洲, 等.
检测多波束测深异常数据的CUBE算法模型解析[J]. 海洋测绘, 2011, 31(4): 1–4.
HUANG Motao, ZHAI Guojun, CHAI Hongzhou, et al. Analysis on the mathematical models of CUBE algorithm for the detection of abnormal data in multibeam echosounding[J]. Hydrographic Surveying and Charting, 2011, 31(4): 1–4. DOI:10.3969/j.issn.1671-3044.2011.04.001 |
| [60] |
黄辰虎, 陆秀平, 侯世喜, 等.
利用CUBE算法剔除多波束测深粗差研究[J]. 海洋测绘, 2010, 30(3): 1–5.
HUANG Chenhu, LU Xiuping, HOU Shixi, et al. Study on detecting outlier of multibeam sounding based on CUBE algorithm[J]. Hydrographic Surveying and Charting, 2010, 30(3): 1–5. DOI:10.3969/j.issn.1671-3044.2010.03.001 |
| [61] | YANG Fanlin, LI Jiabiao, WU Ziyin, et al. A post-processing method for the removal of refraction artifacts in multibeam bathymetry data[J]. Marine Geodesy, 2007, 30(3): 235–247. DOI:10.1080/01490410701438380 |
| [62] | YANG Fanlin, BU Xianhai, MA Yue, et al. Geometric calibration of multibeam bathymetric data using an improved sound velocity model and laser tie points for BoMMS[J]. Ocean Engineering, 2017(145): 230–236. |
| [63] |
赵荻能, 吴自银, 李家彪, 等.
CUBE曲面滤波参数联合优选关键技术及应用[J]. 测绘学报, 2019, 48(2): 245–255.
ZHAO Dineng, WU Ziyin, LI Jiabiao, et al. The key technology and application of parameter optimization combined CUBE and surface filter[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(2): 245–255. DOI:10.11947/j.AGCS.2019.20180082 |



