2. 武汉大学测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
水深测量是海洋测量的主体工作[1-4],由于海面受潮汐作用影响,同一平面位置在不同时刻的测深值呈现动态变化。为获得高精度稳态水深数据,除要保证定位与测深结果的精度外,还须确定测深点在测深时刻的真实海面位置,并将测深值归算至深度基准面,这一过程即为水位改正或称水位控制[5-6]。随着卫星定位技术的广泛应用和测深仪器的智能化发展,测深时刻平面位置的精确获取及瞬时水深的全覆盖探测已得到根本突破[7-10],而水位改正涉及对潮汐的认识、对海面的观测等若干非仪器所能处理的问题。这些技术难题需通过水位改正方法解决,而目前水位改正方法仍停留在历史阶段[11-13],因此水位改正已成为约束水深测量结果精度的主要因素,而且精密海底地形测量对水位改正技术提出了更高的精度要求[14]。
基于相关系数的时差法[15]实现了水位改正由传统的手工作业方式向计算机处理的转变,并首次将离散的潮汐分带模式改进为水位的连续分带模式。潮汐曲线最小二乘比较法[16]利用潮差比、潮时差、基准面偏差三个潮汐比较参数对验潮站间的水位进行配准,为水位改正提供了一种新方法,其优势在于可对水位改正结果进行精度评价。在此基础上,国内专家学者对有关潮汐比较参数的时变规律与影响及模型优化设置等问题[17-18]开展了进一步研究,给出了针对具体方案的指导意见。21世纪以来,以GPS验潮与余水位为代表的现代水位改正方法也得到了一定的发展。GPS技术实现了瞬时潮位的紧密测量,近距离潮位测量中误差约2 cm[19],远距离潮位测量中误差约4 cm[20],GPS验潮需要依靠海域无缝垂直基准转换模型支持,但目前我国海洋统一垂直基准的建设还有待发展完善[22-23]。而余水位法由于目前我国验潮站布设、深度基准模型确定精度较低、区域精密潮汐模型还需进一步提高等问题,水位改正精度受到了限制[24-25]。
天文潮作为水位观测的主体成分与实测水位变化的性质基本一致[26]。本文提出利用天文潮直接计算验潮站间潮时差实施水位改正的方法,对天文潮时差与实际潮时差的差异性质及天文潮时差水位改正效果进行了理论分析与实例验证。
1 原理介绍 1.1 潮汐调和分析方法利用验潮站逐时水位数据可调和分析获得潮汐调和常数,假设水位是由若干分潮叠加而成,则验潮站观测水位可表达为[27-28]
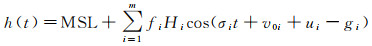 (1)
(1)
式中,h(t)表示水位观测序列;MSL表示平均海面高;f、u表示交点因子与交点订正角;H、g分别表示分潮的振幅与迟角;σ、v0分别表示分潮的角速率与初始天文相角;m表示分潮个数。令ξi=Hicos gi,ai(t)=[fcos(σt+v0+u)]i,ηi=Hisingi,bi(t)=[fsin(σt+v0+u)]i,代入式(1),可得
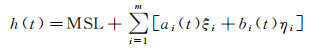 (2)
(2)
根据最小二乘准则,当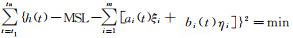
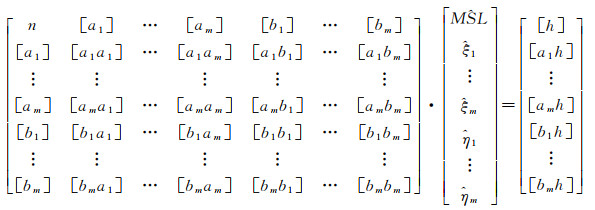 (3)
(3)
 (4)
(4)
式(3)矩阵中[ ]表示各时刻系数值的求和,例如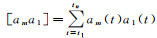
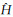
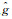
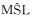
利用调和分析确定的结果可用以确定天文潮,计算公式分别为
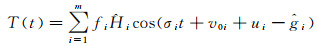 (5)
(5)
由于潮时差的时变特性,本文利用曲线最小二乘法计算验潮站间的潮时差[9, 17],设验潮站A、B的水位观测序列为wA(t)、wB(t),二者之间的关系可用数学模型[9, 29]表示为
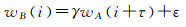 (6)
(6)
式中,γ、τ、ε分别表示两个验潮站水位的潮差比、潮时差、基准偏差,称为潮汐比较参数,在水位曲线图上分别表示为将验潮站A的水位曲线转化为验潮站B的水位曲线时所做的伸缩、水平方向平移与垂直方向平移的变化量。将式(6)线性化后,可按照最小二乘准则计算潮时差,求解具体公式详见文献[21]。
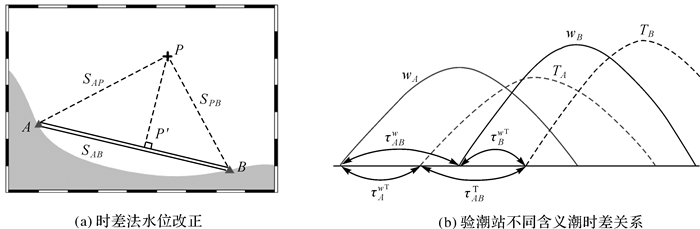
如图 1(a)所示,假设在基准验潮站A、B之间有一待定站P,水位值为wP(t)当P与A、B不共线时,P在A、B连线上的垂足为P′,则时差法水位改正的模型[15]为
|
| 图 1 时差法水位改正与验潮站不同含义潮时差关系 Fig. 1 Diagram of water correction method of TTD and relationship between TTDs in different meaning |
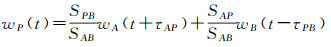 (7)
(7)
式中,τAP、τPB分别为对应验潮站之间的潮时差,确定公式为传统时差法,利用实测水位确定基准站间的潮时差,然后反距离加权内插获得待定点与基准站间的潮时差[5],即
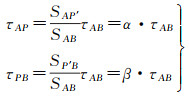 (8)
(8)
传统时差法计算潮时差的方式可理解为当待定站不位于基准站连线上时,则在基准站连线上选择与待定站距离最短的点,认为待定站至基准站的潮时差与该点至基准站的潮时差相同。
当基准站与待定站的潮汐调和常数信息已知时,可利用天文潮计算彼此间的天文潮时差。图 1(b)为验潮站A、B天文潮及实测水位潮时差示意图,其中wA、wB分别表示验潮站实测水位,TA、TB分别表示验潮站天文潮位,τAwT、τBwT分别表示验潮站A、B天文潮与实测水位的潮时差,τABw、τABT表示验潮站A、B间分别利用实测水位、天文潮计算的潮时差。由于τAwT、τBwT都是验潮站A或验潮站B站各自相同验潮站内不同水位的潮时差,故称此类相同验潮站不同水位的潮时差为站内潮时差;由于τABw、τABT是利用不同类型水位资料计算的验潮站间潮时差的结果,故称此类相同水位类型不同验潮站间的潮时差为站间潮时差。如图 1(b)所示,根据潮时差的几何含义是水位曲线的水平平移量,理想情况下,同一时刻站间潮时差与站内潮时差的数学关系可以表示为
 (9)
(9)
整理得
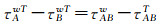 (10)
(10)
故,两相邻验潮站的站内潮时差之差与站间潮时差之差应保持一致。
2 试验分析 2.1 站内潮时差的规律分析在忽略水位观测误差的情况下,实测水位可看作由天文潮与余水位两部分构成,由于余水位的影响,天文潮与实测水位的潮时系统不完全一致,可通过天文潮与实测水位的潮时差衡量两种水位状态下潮时系统的差异。利用连云港(34.750°N,119.417°E)与石臼所(35.383°N,119.550°E)一年的观测时长数据,利用式(9)—式(10),以24 h为时长,逐时计算各验潮站实测水位与天文潮位的潮时差,并统计不同时差区间内各潮时差值出现的频数与累积率,其中天文潮由122个分潮[28]调和常数计算,时差区间是天文潮与实测水位潮时差的绝对值;频数表示在一年的观测期间,各时差区间内潮时差结果的个数,即在指定范围内潮时差出现的次数;累积率为各时差区间频数所占总观测量比例求和。
图 2(a)、(b)为连云港天文潮与实测水位潮时系统差异统计结果,图 2(c)、(d)为石臼所天文潮与实测水位潮时系统差异统计结果。利用各验潮站1981年观测信息确定的122分潮天文潮与实测水位潮时差的样本总量各为8760个,其中超过60%的潮时差结果在0~5 min范围内。石臼所天文潮与实测水位潮时差在10 min以内的累积率可达94.6%,天文潮与实测水位潮时系统相差较小,连云港天文潮与实测水位的潮时系统差异相较于石臼所稍大一些,但潮时差在10 min以内的累积率也超过92%。天文潮是由天体引潮力作用下引起的水位变化现象,实际水位中天文潮占主体,实际水位的变化规律基本遵循天文潮的性质,在连云港与石臼所验潮站对整个潮时系统的影响在15 min以内的累积率可达98%,两个验潮站仅有在少数情况下才会出现天文潮与实测水位潮时差较大的极端情况,可能与极端天气或者观测误差引起的水位异常变化有关。
|
| 图 2 天文潮与实测水位潮时系统差异统计及性质分析 Fig. 2 Difference of tidal time system between astronomical tide and observed Tide |
另外对相邻两个验潮站的天文潮与实测水位潮时差变化情况是否具有相关性进行比较分析,如图 2(e)所示,蓝色实线表示连云港天文潮与实测水位的潮时差,红色虚线表示石臼所天文潮与实测水位的潮时差。图 2(e)中连云港和石臼所验潮站的天文潮与实测水位潮时差变化趋势一致,两验潮站天文潮与实测水位潮时系统的差异同样在空间上具有较好的相关性。当使用数量较少的主要分潮计算天文潮时,实测水位与天文潮的差异比利用122分潮时的差异明显,站内潮时差结果也自然会有所增大,但对于潮汐性质一致的相邻验潮站,站内潮时差的空间相关性仍成立。
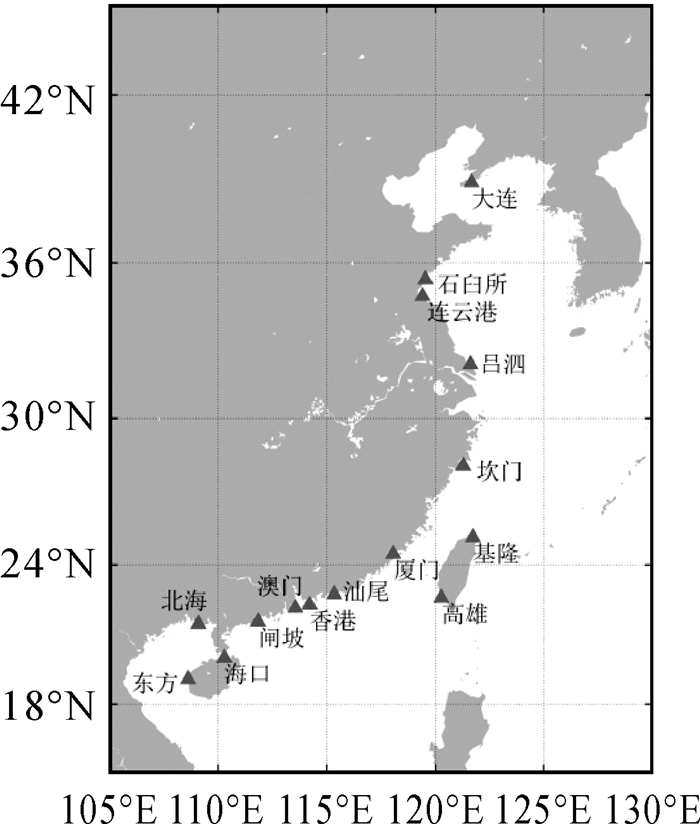
天文潮与实测水位的潮时差正常情况下服从正态分布,假设潮时差母体分布为N(μ, σ2),对1981年中国沿岸15个验潮站的天文潮与实测水位潮时系统的差异作为估计样本,分别统计各站天文潮与实测水位潮时系统差异的均值与标准差。根据数理统计相关结论,余水位引起的天文潮与实测水位潮时系统差异的量值有95%可能性落于(μ-1.96σ, μ+1.96σ)内[30]。验潮站分布及验潮站位置信息及各站余水位引起的潮时系统差异的统计结果,如表 1所示,其中潮汐类型值通过F=(HO1+HK1)/HM2判断:当0 < F≤0.5时,为正规半日潮;当0.5 < F≤2时,为不规则半日潮混合潮;当2 < F≤4时,为不规则日潮混合潮;当F>4时,为正规日潮[31]。为简化表格篇幅,表 1中“正规半”指代正规半日潮、“半混合”指代不规则半日潮混合潮、“日混合”指代不规则日潮混合潮、“正规日”指代正规日潮。
| 序号 | 站名 | 潮汐类型 | 海域 | 纬度N/(°) | 经度E/(°) | μ/min | σ/min |
| 1 | 大连 | 正规半 | 渤海 | 38.933 | 121.667 | 7.4 | 6.4 |
| 2 | 石臼所 | 正规半 | 黄海 | 35.383 | 119.550 | -1.2 | 5.1 |
| 3 | 连云港 | 正规半 | 黄海 | 34.750 | 119.417 | -1.2 | 5.6 |
| 4 | 吕泗 | 正规半 | 东海 | 32.133 | 121.617 | 6.9 | 7.5 |
| 5 | 坎门 | 正规半 | 东海 | 28.083 | 121.283 | 7.0 | 5.4 |
| 6 | 厦门 | 正规半 | 台湾海峡 | 24.450 | 118.067 | 7.1 | 5.6 |
| 7 | 汕尾 | 日混合 | 台湾海峡 | 22.750 | 115.350 | 8.9 | 15.0 |
| 8 | 基隆 | 半混合 | 台湾海峡 | 25.151 | 121.735 | 7.4 | 13.2 |
| 9 | 高雄 | 半混合 | 台湾海峡 | 22.603 | 120.269 | 7.0 | 13.7 |
| 10 | 香港 | 半混合 | 南海 | 22.300 | 114.217 | 9.4 | 14.0 |
| 11 | 澳门 | 半混合 | 南海 | 22.167 | 113.550 | 8.8 | 13.8 |
| 12 | 闸坡 | 半混合 | 南海 | 21.583 | 111.833 | 8.2 | 11.5 |
| 13 | 北海 | 正规日 | 北部湾 | 21.483 | 109.083 | -1.8 | 6.1 |
| 14 | 东方 | 正规日 | 北部湾 | 19.100 | 108.617 | -1.9 | 8.8 |
| 15 | 海口 | 正规日 | 北部湾 | 20.017 | 110.283 | -1.8 | 8.7 |
由表 1的结果可知,中国沿岸验潮站天文潮与实测水位潮时系统差异的均值基本维持在10 min以内,且相邻验潮站保持一致。黄海海域石臼所、连云港站内潮时差的均值最小,约-1 min,渤海海域约为7 min,东海海域及台湾海峡6~9 min不等,大体呈现往南增大的趋势;北部湾海域潮汐类型与其他验潮站不同,站内潮时差平均约为-2 min。从汕尾向南至闸坡,以及台湾岛的基隆、高雄,验潮站天文潮与实测水位的潮时差变化幅度明显大于其他验潮站,标准差可达其他海区验潮站的1.5倍。站内潮时差是利用观测水位与天文潮计算而得,水位变化的规律决定了潮时差确定的结果,在汕尾南至闸坡以及台湾海峡这一区域潮汐、气象变化复杂且台风频发,验潮站水位出现急速的增、减水现象较为频繁,使得实测水位与天文潮位的差异大于其他海域,最终导致了站内潮时差的标准差大于其他海域。
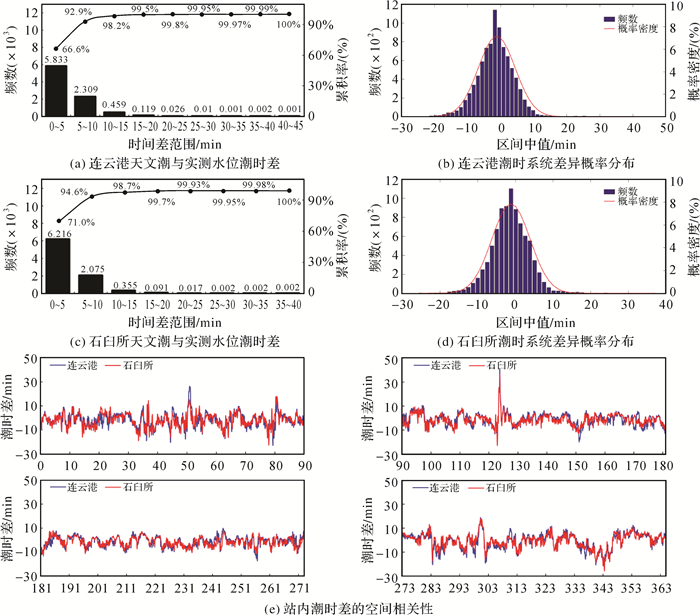
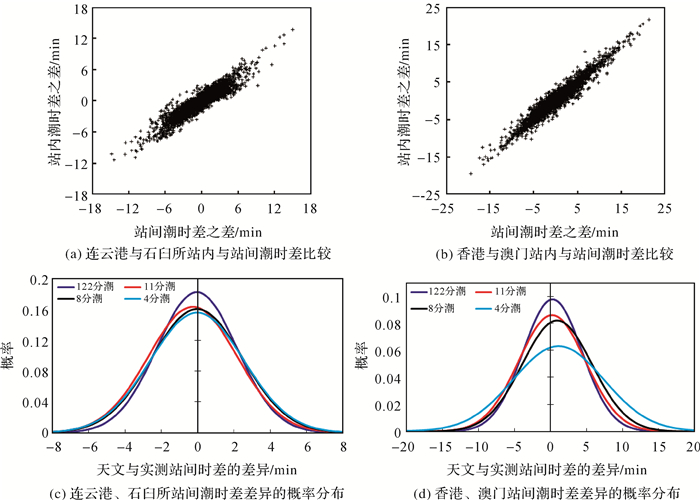
2.2 站间潮时差的差异分析选择距离较近的连云港与石臼所、香港与澳门两组验潮站数据,对各组站间潮时差的差异情况进行统计分析。图 3(a)、(b)为各组验潮站站内潮时差与站间潮时差的差异值比较,试验结果与式(10)的推导吻合,相邻验潮站站间潮时差的差异应与各验潮站站内潮时差的差异相一致。连云港与石臼所(距离71.3 km)利用实测水位与天文潮位计算站间潮时差的结果最大相差约13 min,平均差异为-0.03 min,差异的标准差为2.18 min;香港、澳门(距离70.3 km)利用实测水位与天文潮位计算的站间潮时差结果最大差异约为20 min,平均差异为0.26 min,差异的标准差为4.08 min,大部分情况下,实测水位与天文潮位站间潮时差的差异相对于站间潮时差本身而言量值较小。
|
| 图 3 站间潮时差差异与站内潮时差差异比较 Fig. 3 TTD between astronomical tide and observed water level on adjacent tidal stations |
图 3(a)、(b)中的结果是利用122个分潮计算的天文潮,在调和分析的过程中,可分离的分潮个数跟观测资料的时长与观测间隔有关[27-28]。在122个分潮中仅个别振幅较大的主要分潮对水位变化的影响较为显著。以试验中的两组验潮站为例,连云港、石臼所的潮汐类型为正规半日潮,半日分潮振幅较为显著,M2分潮的振幅最大,约为其余分潮振幅的3倍以上,其余振幅较大的分潮有S2、N2、O1、K1,长周期分潮Sa也与全日分潮O1具有相同量级,浅水分潮振幅较大的有M4、MS4分潮;香港、澳门的潮汐类型为不规则半日潮混合潮,M2、K1、O1分潮振幅占优,浅水分潮同样是M4、MS4分潮的振幅较大。
利用两组验潮站的调和常数对不同分潮选择模式下的天文潮与实测水位的站间潮时差差异进行分析。统计一年内连云港与石臼所不同分潮选择模式下,天文潮站间潮时差与实测站间潮时差计算结果的差异情况,如表 2所示,11分潮选择Sa、M2、S2、N2、P2、K1、O1、P1、Q1、M4、MS4 11个主要分潮,8分潮选择的是11分潮中主要的全日、半日分潮,4分潮选择的是M2、S2、K1、O1分潮,集中范围表示正态分布90%概率下站间潮时差差异的范围值,两组验潮站不同分潮选择下的站间潮时差差异概率分布如图 3(c)、(d)所示。
| 验潮站选择模式 | (a)连云港与石臼所 | (b)香港与澳门 | |||||||
| 122分潮 | 11分潮 | 8分潮 | 4分潮 | 122分潮 | 11分潮 | 8分潮 | 4分潮 | ||
| 最大偏差 | 12.6 | 12.5 | 12.8 | 12.3 | 21.6 | 21.4 | 23.7 | 29.3 | |
| 最小偏差 | -13.8 | -13.9 | -14.4 | -14.6 | -20.2 | -20.3 | -18.4 | -25.7 | |
| 平均偏差 | -0.03 | -0.26 | -0.03 | -0.02 | 0.27 | 0.20 | 0.90 | 1.10 | |
| 标准差 | 2.18 | 2.44 | 2.48 | 2.56 | 4.08 | 4.63 | 4.84 | 6.29 | |
| 90%范围 | -3.6~3.6 | -4.3~3.8 | -4.1~4.1 | -4.2~4.2 | -6.5~7.0 | -7.4~7.8 | -7.1~8.9 | -9.2~11.5 | |
如表 2及图 3(c)、(d)所示,122个分潮确定的天文潮在计算潮时差时与实测水位计算的潮时差相差90%在8 min以内,其中连云港、石臼所天文潮与实测站间潮时差差异较小,香港、澳门的差异稍大。随着选择的分潮个数减少,站间潮时差的差异逐渐增大,但两组试验中8个主要分潮的结果与11个主要分潮的结果基本一致。天文潮计算的潮时差与实测水位计算的潮时差之间的差异与验潮站潮汐性质密切相关,连云港、石臼所潮位变化规律潮汐性质稳定,不同分潮选择对潮时差异的影响较小;香港、澳门验潮站属于不规则半日潮海区,不同分潮的选择对潮时差的影响较为明显,特别是4个主要分潮确定的潮时差与实测潮时差的差异的标准差比其他分潮选择方式的结果大近2 min,导致其90%概率分布范围为-9.2~11.5 min,比122分潮结果范围扩大了7.2 min,比11分潮与8分潮结果范围分别扩大了5.5 min、4.7 min。
利用天文潮计算站间潮时差与实测水位计算结果的差异与各验潮站的站内潮时差的差异变化基本一致,而且相邻验潮站的站内潮时差彼此间具有较明显的相关性。天文潮与实测水位站间潮时差的差异与验潮站性质、分潮选择等因素有关,当仅利用主要分潮计算天文潮进而确定站间潮时差时,11分潮与8分潮的结果较为接近,与实测潮时差的差异大部分情况小于10 min,当再减少分潮个数,仅利用4个主要分潮(M2、S2、K1、O1)计算潮时差时,在不规则半日潮海域天文潮与实测潮时差结果的差异较大,在规则半日潮海域影响较小,与其他分潮确定结果相当。
2.3 水位改正效果差异分析选择图 4中的两组验潮站设计水位改正效果差异分析的实验,其中图 4(a)中以连云港(A)、古镇口(B)作为基准站,以石臼所作为待定站;图 4(b)中以防城港(A)、草潭(B)作为基准站,北海、涠洲作为待定站,各验潮站均有一个月的逐时水位观测数据及主要分潮的调和常数信息,验潮站的相关信息如表 3所示,其中α、β、h分别表示待定站与基准站A、B的潮时差内插比例系数以及到基准站间连线的距离。
|
| 图 4 水位改正试验验潮站分布 Fig. 4 Distributions of two groups of tide gauges for water correction experiment |
| 基准站A坐标 | 基准站B坐标 | 待定站坐标 | α | β | h/km |
| 连云港(34.75°N, 119.42°E) | 古镇口(35.72°N, 119.98°E) | 石臼所(35.38°N, 119.55°E) | 0.58 | 0.42 | 19.3 |
| 防城港(21.69°N, 108.34°E) | 草潭(21.26°N, 109.78°E) | 北海(21.48°N, 109.08°E) | 0.53 | 0.47 | 6.4 |
| 涠洲(21.00°N, 109.11°E) | 0.63 | 0.37 | 46.1 |
天文潮时差水位改正与传统时差法的差别在于潮时差的确定方式,传统时差法是利用基准站连线上与待定站距离最近的位置代替待定站进行水位改正,即待定站与基准站的潮时差确定是通过按距离内插计算,而本文提出的天文潮时差方法是利用调和常数信息对基准站至待定站的潮时差的直接确定,作为时差法水位改正中使用的唯一参数,潮时差的差异将影响水位改正的效果。因此,试验主要从两个方面比较水位改正的效果,一个是对潮时差确定结果差异的比较,另一个是对水位改正结果质量的比较,试验结果如表 4所示。
| 待定站 | 潮时差(基准站A)/min | 潮时差(基准站B)/min | 水位改正结果/cm | |||||||||
| 传统 | 8分潮 | 4分潮 | 传统 | 8分潮 | 4分潮 | 传统 | 8分潮 | 4分潮 | ||||
| 石臼 | max | 16.3 | 3.8 | 8.2 | 9.5 | 6.3 | 8.8 | 14.7 | 8.2 | 11.6 | ||
| RMS | 7.1 | 1.8 | 2.0 | 4.3 | 2.5 | 3.2 | 8.2 | 4.8 | 6.3 | |||
| 北海 | max | 6.1 | 4.7 | 6.9 | 5.9 | 4.2 | 5.5 | 15.3 | 8.9 | 13.2 | ||
| RMS | 4.5 | 2.6 | 4.1 | 4.7 | 2.7 | 3.0 | 5.3 | 2.3 | 3.4 | |||
| 涠洲 | max | 24.3 | 5.1 | 7.4 | 16.2 | 6.2 | 5.8 | 25.9 | 9.4 | 11.6 | ||
| RMS | 14.0 | 3.0 | 3.7 | 13.0 | 3.9 | 4.5 | 5.3 | 3.6 | 5.6 | |||
将利用实测水位计算的站间潮时差视为潮时差的真值,将实测水位视为水位改正的真值,则表 4中max表示计算结果与真值的最大偏差,RMS表示确定参数的中误差[32]。在潮时差确定方面,传统时差法确定的基准站与待定站间潮时差差异最大值均大于天文潮直接计算的结果,其中在涠洲站传统方法计算的潮时差最大差异达到了24 min,而防城港与涠洲间潮时差的平均值为29 min,最大相对误差达到了82%,北海传统方法确定的站间潮时差效果相比其他待定站情况较好的原因是北海位置近似处于防城港与草潭站连线上,更符合潮时差线性传播的假设。利用8个主要分潮直接确定潮时差规避了潮时差是否线性传播这一问题,3个待定站潮时差的最大差异约为6 min,潮时差确定精度明显优于传统方法,当选用的分潮个数进一步减少,仅用4个主要分潮计算站间潮时差时,效果相比8分潮稍差,但仍比传统方法的结果更接近潮时差真值。在水位改正方面,利用天文潮确定的潮时差进行水位改正相比于传统时差法,水位改正中误差均有所降低,提高了水位改正带精度与合理性,而且利用8个主要分潮与利用4个主要分潮的结果精度一致。利用8个主要分潮进行天文潮时差水位改正,与实测水位的最大偏差低于10 cm,中误差在5 cm以内。
天文潮时差水位改正法改善了传统时差法水位改正的效果,证明了利用天文潮时差实施水位改正的可行性。天文潮时差法与传统时差法的使用条件类似,需要水位改正海域内潮汐性质及水位变化规律一致,使用时应对当地潮汐性质、验潮站分布、水位变化特征等情况进行具体分析,当条件满足时,可依靠基准站实测水文信息与现有潮汐模型或海洋数值模型提供的主要分潮调和常数信息,构建基于验潮基准站的天文潮时差模型实现整体的海域水位连续时空内插。
3 结论本文对利用天文潮替代实测水位计算潮时差以改进水位改正时差法等问题展开相关研究,得到如下结论:
(1) 我国沿海验潮站天文潮与实测水位间的站内潮时差空间上具有较为明显的相关性,且各区域存在差异,黄海海域验潮站的站内潮时差均值最小,约为-1 min,渤海海域平均约为7 min,东海海域及台湾海峡均值6~9 min不等,北部湾海域潮汐类型与其他验潮站不同,站内潮时差平均约为-2 min。
(2) 天文潮与实测水位站间潮时差之差与两验潮站的站内潮时差之差基本变化一致,而且选择不同分潮个数确定的天文潮替代实测水位计算潮时差对于不同海域效果各异。正规半日潮海域,连云港、石臼所4种分潮选择下的替代效果较好且一致,基本带来潮时差的偏差在-4~4 min范围内,但不规则半日潮海域香港、澳门站间潮时差确定偏差较大,其中122分潮的偏差标准差约为4 min,效果较好,11分潮与8分潮效果接近,偏差标准差均接近5 min,而4分潮的差异稍大,偏差标准差约6.3 min。
(3) 与传统时差法相比,本文方法在潮时差的确定方式上规避了以基准站间连线上某点潮时差代替待定点的问题,而是利用天文潮直接计算待定站的潮时差参数,提高了潮时差确定的精度。试验中,3个待定站8分潮水位改正的中误差在5 cm以内,精度比传统时差法提高了近一倍,4分潮水位改正效果略好,基本与传统方法达到了相当的精度,证明了利用天文潮时差进行水位改正的可行性。
| [1] |
刘雁春.
海洋测深空间结构及其数据处理[M]. 北京: 测绘出版社, 2002.
LIU Yanchun. Space structure and data processing in marine sounding[M]. Beijing: Surveying and Mapping Press, 2002. |
| [2] | LACHAPELLE G. Hydrographic surveying[M]. Canada: The University of Calgary, 1996. |
| [3] | International Hydrographic Organization. S-44 IHO standards for hydrographic surveys[S]. 4th ed. Monaco: International Hydrographic Bureau, 1998. |
| [4] |
翟国君, 黄谟涛.
海洋测量技术研究进展与展望[J]. 测绘学报, 2017, 46(10): 1752–1759.
ZHAI Guojun, HUANG Motao. The review of development of marine surveying technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1752–1759. DOI:10.11947/j.AGCS.2017.20170309 |
| [5] |
暴景阳, 刘雁春.
海道测量水位控制方法研究[J]. 测绘科学, 2006, 31(6): 49–51.
BAO Jingyang, LIU Yanchun. A study of water level control for hydrographic survey[J]. Science of Surveying and Mapping, 2006, 31(6): 49–51. DOI:10.3771/j.issn.1009-2307.2006.06.013 |
| [6] |
刘雁春, 肖付民, 暴景阳.
面向21世纪的海洋测深(改正)新技术[J]. 地球科学进展, 1996, 11(3): 314–317.
LIU Yanchun, ZIAO Fumin, BAO Jingyang. New techniques of marine sounding correction for the 21st century[J]. Advance in Earth Sciences, 1996, 11(3): 314–317. DOI:10.3321/j.issn:1001-8166.1996.03.015 |
| [7] |
刘经南, 方媛, 郭迟, 等.
位置大数据的分析处理研究进展[J]. 武汉大学学报(信息科学版), 2014, 39(4): 379–385.
LIU Jingnan, FANG Yuan, GUO Chi, et al. Research progress in location big data analysis and processing[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 379–385. |
| [8] |
赵建虎, 欧阳永忠, 王爱学.
海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1786–1794.
ZHAO Jianhu, OUYANG Yongzhong, WANG Aixue. Status and development tendency for seafloor terrain measurement technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1786–1794. DOI:10.11947/j.AGCS.2017.20170276 |
| [9] |
许军.水下地形测量的水位改正效应研究[D].大连: 海军大连舰艇学院, 2009. XU Jun. Research on the effects of water level correction on underwater topographic survey[D]. Dalian: PLA Dalian Naval Academy, 2009. |
| [10] | LEA S H. Hydrographic surveying:methods, tables and forms of notes[M]. [S.l.]: Andesite Press, 2015. |
| [11] |
暴景阳, 许军.
海道测量水位控制的技术体系及标准更新[J]. 海洋测绘, 2016, 36(6): 1–6.
BAO Jingyang, XU Jun. Technical framwork and specification revision for water level control in hydrographic survey[J]. Hydrographic Surveying and Charting, 2016, 36(6): 1–6. DOI:10.3969/j.issn.1671-3044.2016.06.001 |
| [12] |
暴景阳, 许军, 于彩霞.
海洋空间信息基准技术进展与发展方向[J]. 测绘学报, 2017, 46(10): 1778–1785.
BAO Jingyang, XU Jun, YU Caixia. Technical progress and development directions of oceanic spatial information datum[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1778–1785. DOI:10.11947/j.AGCS.2017.20170371 |
| [13] |
杨元喜, 徐天河, 薛树强.
我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1–8.
YANG Yuanxi, XU Tianhe, XUE Shuqiang. Progresses and prospects in developing marine geodetic datum and marine navigation of China[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 1–8. DOI:10.11947/j.AGCS.2017.20160519 |
| [14] |
暴景阳.为建设海洋强国提供基础技术支撑[N].中国国土资源报, 2018-05-03(05). BAO Jingyang. Provide basic technical support for building a powerful marine country[N]. China Land and Resources News, 2018-05-03(05). |
| [15] |
谢锡君, 翟国君, 黄谟涛.
时差法水位改正[J]. 海洋测绘, 1988, 8(3): 22–26.
XIE Xijun, ZHAI Guojun, HUANG Motao. Water correction in time-difference method[J]. Hydrographic Surveying and Charting, 1988, 8(3): 22–26. |
| [16] |
刘雁春, 暴景阳.
海道测量水位改正数学模型[J]. 海洋测绘, 1992, 12(4): 17–22.
LIU Yanchun, BAO Jingyang. Mathematical model of water correction in hydrographic surveying[J]. Hydrographic Surveying and Charting, 1992, 12(4): 17–22. |
| [17] |
许军, 刘雁春, 暴景阳, 等.
最小二乘水位拟合模型的参数时变规律研究[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1418–1421, 1426.
XU Jun, LIU Yanchun, BAO Jingyang, et al. Temporal variation law of parameters of least square fitting model[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1418–1421, 1426. |
| [18] |
许军, 暴景阳, 章传银, 等.
最小二乘水位拟合法的应用优化设置[J]. 海洋测绘, 2016, 36(1): 21–24.
XU Jun, BAO Jingyang, ZHANG Chuanyin, et al. Optimal application of the least square fitting method[J]. Hydrographic Surveying and Charting, 2016, 36(1): 21–24. DOI:10.3969/j.issn.1671-3044.2016.01.005 |
| [19] |
赵建虎, 张红梅, CLARKEJ E H.
测船处瞬时潮位的GPS精密确定[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1067–1070.
ZHAO Jianhu, ZHANG Hongmei, CLARKE J E H. Determination of precise instantaneous tidal level at vessel[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1067–1070. |
| [20] |
赵建虎, 王胜平, 张红梅, 等.
基于GPSPPK/PPP的长距离潮位测量[J]. 武汉大学学报(信息科学版), 2008, 33(9): 910–913.
ZHAO Jianhu, WANG Shengping, ZHANG Hongmei, et al. Long-distance and on-the-fly GPS tidal level measurement based on GPS PPK/PPP[J]. Geomatics and Information Science of Wuhan University, 2008, 33(9): 910–913. |
| [21] |
柯灏.海洋无缝垂直基准构建理论和方法研究[D].武汉: 武汉大学, 2012. KE Hao. Research on the theory and implementation method of marine seamless vertical reference surface[D]. Wuhan: Wuhan University, 2012. |
| [22] |
柯灝, 吴敬文, 李斐, 等.
基于潮波运动三维数值模拟的海洋连续深度基准面建立方法研究[J]. 地球物理学报, 2018, 61(6): 2220–2226.
KE Hao, WU Jingwen, LI Fei, et al. Study on the establishment of the oceanic continuous chart datum based on three-dimensional numerical simulation of tidal wave motion[J]. Chinese Journal of Geophysics, 2018, 61(6): 2220–2226. |
| [23] |
周兴华, 付延光, 许军.
海洋垂直基准研究进展与展望[J]. 测绘学报, 2017, 46(10): 1770–1777.
ZHOU Xinghua, FU Yanguang, XU Jun. Progress and prospects in developing marine vertical datum[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1770–1777. DOI:10.11947/j.AGCS.2017.20170322 |
| [24] | HESS K. Water level simulation in bays by spatial interpolation of tidal constituents, residual water levels, and datums[J]. Continental Shelf Research, 2003, 23(5): 395–414. DOI:10.1016/S0278-4343(03)00005-0 |
| [25] |
许军, 暴景阳, 刘雁春, 等.
基于区域潮汐场模型的水位控制可行性研究[J]. 海洋测绘, 2011, 31(4): 8–12.
XU Jun, BAO Jingyang, LIU Yanchun, et al. Research on the feasibility of water level control based on tide model[J]. Hydrographic Surveying and Charting, 2011, 31(4): 8–12. DOI:10.3969/j.issn.1671-3044.2011.04.003 |
| [26] |
黄祖珂, 黄磊.
潮汐原理与计算[M]. 青岛: 中国海洋大学出版社, 2005.
HUANG Zuke, HUANG Lei. Tidal theory and calculation[M]. Qingdao: China Ocean University Press, 2005. |
| [27] |
方国洪, 郑文振, 陈宗镛, 等.
潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986.
FANG Guohong, ZHENG Wenzhen, CHEN Zongyong, et al. Analysis and prediction of tide and tidal current[M]. Beijing: Ocean Press, 1986. |
| [28] |
暴景阳, 许军.
卫星测高数据的潮汐提取与建模应用[M]. 北京: 测绘出版社, 2013.
BAO Jingyang, XU Jun. Tide analysis from altimeter data and the establishment and application of tide model[M]. Beijing: Surveying and Mapping Press, 2013. |
| [29] |
刘雁春.
海道测量基准面传递的数学模型[J]. 测绘学报, 2000, 29(4): 310–316.
LIU Yanchun. Mathematical models for hydrographic datum transfer[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(4): 310–316. DOI:10.3321/j.issn:1001-1595.2000.04.006 |
| [30] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差[M]. 2版. 北京: 测绘出版社, 1992.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized survey adjustment[M]. 2nd ed. Beijing: Surveying and Mapping Press, 1992. |
| [31] |
付延光, 周兴华, 许军, 等.
利用TOPEX/Poseidon和Jason-1高度计数据提取中国南海潮汐信息[J]. 武汉大学学报(信息科学版), 2018, 43(6): 901–907.
FU Yanguang, ZHOU Xinghua, XU Jun, et al. Extraction of tidal information in the south China sea based on TOPEX/Poseidon and Jason-1 altimeter data[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 901–907. |
| [32] |
武汉大学测绘学院测量平差学科组.
误差理论与测量平差基础[M]. 2版. 武汉: 武汉大学出版社, 2009.
Discipline Group of Surveying Adjustment of School of Geodesy and Geomatics of Wuhan University. Error theory and fundation of surveying adjustment[M]. 2nd. Wuhan: Wuhan University Press, 2009. |


