空间分辨率限制及地物复杂多样性,使得高光谱遥感图像像元中通常包含多种地物成分,形成所谓混合像元[1-2]。像元的“解混”是实现地物分类与目标识别等高光谱遥感定量化、精细化应用的关键步骤之一。非负矩阵分解(non-negative matrix factorization,NMF)适合处理高维海量数据,能够减小对先验知识的依赖[3],同时与线性混合模型的数学形式相似,因此,基于NMF的线性盲解混算法,逐渐成为高光谱解混领域的研究热点[4]。文献[5—8]表明,盲解混算法是指不依赖大量先验知识,只根据混合像元数据本身即可同时估计出端元光谱信息和丰度信息的一类非监督解混算法。
近年来,相关性分析开始出现在高光谱像元解混研究中[9-12]。文献[13]通过添加空间相关性约束项和训练数据的空间信息,提出了一种新的高光谱解混方法。文献[14]利用先验概率密度函数表达两个相邻区域的空间相关程度,提出了一种区域相关的NMF解混算法(area-correlated spectral unmixing method based on Bayesian nonnegative matrix factorization, ACBNMF)。文献[15]通过联合最小化光谱相关度函数和NMF误差函数,提出了一种最小化光谱相关度约束的NMF方法(minimum spectral correlation constraint NMF, MSCCNMF)。文献[16]基于图像空间特征和联合稀疏解混思想,提出一种基于高光谱图像空间相关性度量的多任务联合稀疏解混方法。
上述基于相关性分析的解混算法存在如下问题:①缺少针对高光谱遥感图像在空间和光谱两个维度典型相关性特征的综合分析与利用[15-16];②属于监督类算法,需要大量难以获取的先验知识,一定程度上限制了算法的适用范围[13-14]。因此,有必要深入挖掘并充分利用高光谱遥感图像中蕴含的各类相关性特征,探索其在降低先验知识依赖程度,改善解混算法性能方面的应用潜力。
本文针对NMF在线性盲分解中存在的目标函数非凸导致的局部极小问题,综合利用马尔科夫随机场(Markov random field, MRF)模型[17]和信号预测度技术[18],提出一种基于空间与谱间相关性模型的NMF线性盲分解算法(spatial and spectral correlation model-based NMF pixel unmixing algorithm,S2CNMF)。
1 标准NMF线性盲分解模型及存在的主要问题 1.1 NMF线性盲分解模型 1.1.1 线性光谱混合模型(linear spectral mixture model,LSMM)LSMM的数学形式如式(1)所示
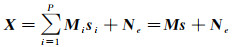 (1)
(1)
式中,X是L(L为波段数量)维的已知高光谱图像;M是L×P(P为端元数目)的端元矩阵,每一列代表一个端元的光谱向量;向量s是像元中各端元的丰度;Ne是L维的高斯随机噪声。如果把高光谱图像的全部C(假设C为像元个数)个像元均考虑进式(1),则式(1)可扩展为
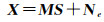 (2)
(2)
式中,X∈RL×C,R代表非负矩阵,列向量为每个像元的光谱值;S∈RP×C表示丰度矩阵或称混合矩阵。S存在两个约束条件,非负性约束(Si, j≥0, i=1, 2, …, P, j=1, 2, …, C)和全加性约束
已知非负矩阵X1∈Rm×n和正整数p(p < min(m, n)),同时寻找元素均为非负的矩阵X2∈Rm×p和X3∈Rp×n,使其满足
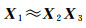 (3)
(3)
或等价表示为
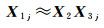 (4)
(4)
式中,X1j是X1的第j列列向量,X3j∈Rp,其中p为矩阵X2的期望秩,一般可由先验信息或X1本身确定。解NMF问题的常用方法是通过最小化X1与X2X3之间的欧氏距离,寻求最优分解,如式(5)所示,其中,‖·‖F2代表Frobenius模。目标函数则如式(6)所示,一般采用乘法准则进行迭代
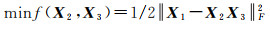 (5)
(5)
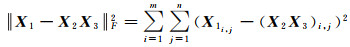 (6)
(6)
NMF存在局部极小问题,如果不采取对应措施,将损害NMF线性盲分解的精度和稳定性。
NMF的求解过程等价于通过迭代求目标函数最小值的过程,理想情况是目标函数为凸函数。函数凸性是数学分析中的一个重要概念,凸函数的重要性质是:任何局部极小同时也是全局最小。只要NMF的目标函数取得局部极小收敛,就说明获取了全局最小值,也即全局最优解。文献[19]给出了标准NMF目标函数(5)的凸性判定过程与收敛性证明,结论如下:NMF目标函数分别对于端元光谱矩阵和丰度矩阵都是凸函数,但同时对于二者是非凸函数。也就是说,式(5)取局部极小值时,端元光谱矩阵和丰度矩阵的解并不是二者的全局最优解。“非凸性”会使收敛结果沦为局部极小,增大解的不确定性并降低算法整体精度。
此外,高光谱图像同时包含丰富的空间特征和光谱特征,对于混合像元的组成结构和解混过程都具有重要影响。但是,标准NMF只将高光谱图像视为无规律的光谱测量记录,忽略其空间特征,也可能导致解混结果出现较大偏差。
由此可见,如果能够深入挖掘高光谱图像中蕴含的相关性特征,建立对应约束条件,沿着符合地物真实情况的方向对NMF盲分解过程进行引导,将有助于消除或弱化上述问题带来的不利影响,改善算法性能。
2 基于MRF改进模型的空间相关性模型在高光谱遥感图像中,每类地物的空间分布往往都有各自主导区域,并在各自主导区域内部连续分布,导致相邻像元观测数值(DN值、辐亮度或地表反射率等)之间存在近似性和相互依赖性,是地物蕴含于混合像元及其形成过程的重要物理属性。论文选择以MRF模型为载体,在解混算法中显式且定量地描述相邻像元的空间相关特征。
MRF包含“Markov性质”和“随机场”两个要素,可简单解释为具有Markov性质的随机场。MRF的具体定义与主要性质可参考文献[20]。二维数字图像可看作随机场,空间相关性质也可类比于Markov性质(仅相邻时刻间的状态相关),则空间相关特征显著的高光谱遥感图像可用MRF近似表示。图像的空间能量大小与地物的空间变化频率和幅度成正比。对于空间相关特征显著的高光谱图像,解混结果中空间能量越小,越可能接近地面空间能量分布的真实情况。本文以文献[21]关于MRF的图像分割模型为基础,建立反映图像空间相关特征的能量函数模型如下
 (7)
(7)
模型将能量函数分为EFeature和ERelevance两部分,能够反映像元本身以及与相邻像元之间两种特征。EFeature描述像元本身特征,只和观测值分布有关。假设观测图像含有高斯噪声,可得能量函数EFeature
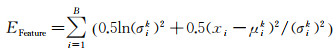 (8)
(8)
式中,B为波段数;μik和σik分别表示从图像(X=x)中提取出的特征向量中第k个特征的均值和标准差。
ERelevance描述像元与邻域间的相关性。由于MRF模型在求解最大后验概率估计的过程中使用一致平滑假设,会在图像边缘处造成过平滑。为克服过平滑,文献[22]提出的基于DA-GMRF的无监督图像分割方法,利用间断自适应(discontinuity-adaptive, DA)思想,基于边缘信息定义基团势能,即首先运用边缘算子对图像提取边缘,得到二值边缘图,然后定义能量函数ERelevance为
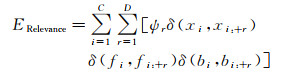 (9)
(9)
式中,C为图像中像元数;D=2表示一邻域模型,D=4表示二阶邻域模型;{ψ1, ψ2, …, ψD}是权重系数;xi为像素i的灰度值;fi为基团中像素i的标记值;bi为像素i处的边缘值。当xi=xi:+r时,δ(xi, xi:+r)=-1,否则δ(xi, xi:+r)=0;当fi=fi:+r时,δ(fi, fi:+r)=-1,否则δ(fi, fi:+r)=1;当bi=bi:+r时,δ(bi, bi:+r)]=1,否则δ(bi, bi:+r)]=0。式(9)考虑了平滑约束在图像边缘处的自适应性,避免了边缘处的过平滑。
文中假设所有高光谱图像行列数均相等,行列数不相等的图像可作为多个行列数相等子图像的组合。基于上述假设,下文中所有丰度矩阵S均为方阵,即存在逆矩阵。
设U为分离矩阵,即丰度矩阵S的逆,Y为端元矩阵M的估计,由式(3)可得
 (10)
(10)
 (11)
(11)
式(11)及后续公式中,统一用A表示高光谱图像矩阵。下面以U为求解对象,通过NMF和MRF约束交替运行的方式计算U。
为简化推导过程,这里仅考虑一阶邻域系统相关性。如果把所有权重系数ψ设置为1,用W表示特征向量的均值矩阵,同时假设特征向量中各个特征的标准差σk相等,结合式(8)和式(9)可以推出E(U)如式(12)所示
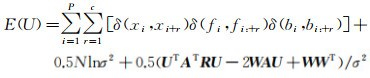 (12)
(12)
能量函数E(U)取最小值时,MRF模型描述的“空间能量”最小,空间分布情况最理想,此时式(12)中E(U)关于U的偏导数应为零,据此可最终推导出U的解如式(13)所示
 (13)
(13)
谱间相关性源于传感器的频谱交叠,一般而言,光谱分辨率越高,谱间相关越强。分段平滑即光谱曲线在几个特定的光谱范围内具有明显的平滑特征,在光谱范围边界处平滑特征减弱,存在不同程度的突变。该特征反映了谱线的结构性和冗余性,即根据某波长位置的数值可大致预测出附近其他波长位置的数值。真实高光谱遥感数据中,源于谱间相关的分段平滑特征非常显著和普遍。
信号预测度也可称为复杂度映射(complexity pursuit),利用信号的可预测性(predictability)度量信号复杂度,通过在混合信号的变换中寻找具有最小复杂度的信号来达到恢复原始信号的目的,其中预测度反映了利用信号本身某些部分预测其他部分的难易程度。
这里仍然用M表示高光谱数据的端元矩阵,用F(M)表示高光谱图像端元光谱信号的预测度,则F(M)的计算公式为
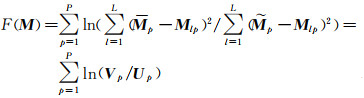 (14)
(14)
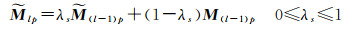 (15)
(15)
式中,分子Vp表示信号Mp的方差(Mp是Mlp的均值),它保证信号序列不会变为常数序列;分母Up表示信号的“粗糙度”,信号越粗糙,Up越大;相反地,信号越平滑,Up越小。实际上,Up反映了M先前信号序列的短期移动平均值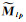
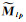
最大化Vp/Up需要同时满足两个条件:
(1) Mlp存在一定的变化范围;
(2) Mlp的值在时间上变化“缓慢”。
由于Mlp代表高光谱图像的端元光谱信号,绝大多数的端元光谱都具有分段平滑特征,即同时具备变化性和平滑性,很好地满足了上述两个条件。因此,可利用预测度函数定量描述端元光谱的分段平滑特征,作为NMF目标函数的新约束项。加入光谱预测度约束后的NMF目标函数为
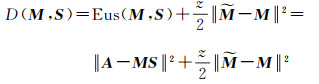 (16)
(16)
式中, z为规则化参数;
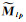
 (17)
(17)
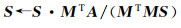 (18)
(18)
式中,MT为M的转置矩阵。
此外,为满足ASC,S需要被归一化,归一化计算公式如下
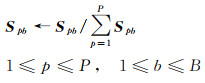 (19)
(19)
为减小与已有约束(NMF目标函数的欧氏距离约束或KL散度约束,非负约束、全加约束等)的相互干扰,S2CNMF算法中的空间相关约束采用了与NMF目标函数交替运行的独立函数形式,即迭代解混过程由含有谱间相关约束的NMF步骤和空间相关约束步骤交替组成。
基于MRF的空间相关特征约束,以及基于预测度技术的谱间相关约束,针对NMF解混存在的问题,分别引入了反映高光谱图像特征的不同约束条件,但二者作用目标和侧重点所有不同。前者由于与NMF目标函数独立、交替运行,主要侧重于修正NMF流程在端元空间能量分布方面的偏差,提高解混精度;而后者存在于NMF目标函数内部,主要侧重于修正NMF目标函数的非凸性,确保并加快NMF目标函数的收敛。
可得S2CNMF算法步骤如下:
(1) 利用基于最小误差的高光谱信号识别法(hyperspectral signal identification by minimum error,HySime)估算端元数量P;
(2) 初始化端元矩阵M和丰度矩阵S;
(3) 含有谱间相关约束的NMF迭代:根据更新规则式(17)和式(18)分别计算端元矩阵M和丰度矩阵S的迭代结果,并利用M和S计算分离矩阵U的迭代结果;
(4) 空间相关约束:归一化分离矩阵U的每一列,同时估计像元特征向量的均值矩阵W,然后计算U;
(5) 重复步骤(3)和(4),继续迭代,直到各自的停止准则同时满足,得到一个估计的成分,将其转换为矩阵,即获得一个端元分布。继续迭代,直至满足阈值条件(预先设置的一个很小的正数如10-4等,作为迭代停止条件),得到端元分布的估计结果。
其中,端元数量估计算法HySime是一种估计高光谱信号子空间的方法,计算过程复杂,但不需任何参数,具有自适应性,估计准确度较高。文献[23]给出了该算法的原理与实现过程。
算法步骤(3)中NMF迭代的目标函数收敛性证明可参见文献[24];步骤(3)收敛保证了分离矩阵U的迭代结果收敛,则算法步骤(4)中对U的每一列进行归一化得到的特征向量均值矩阵W也是收敛的;容易证明式(13)关于W收敛,因此步骤(4)中的目标函数收敛。由于步骤(3)和步骤(4)共同组成了一个带有初始边界值的并行交替迭代法,该算法可抽象为一种Dirichlet-Neuman(D-N)交替迭代法,结合文献[25]对于D-N交替迭代法及其收敛性的分析结果,可以证明S2CNMF算法的收敛性。
需要进一步说明的是,本文算法主要针对空间相关程度较高,或者空间相关程度一般但谱间相关程度较高的高光谱遥感场景;反之也成立。也就是说,只有空间、谱间两种相关特征同时不显著时,才会严重影响算法性能,多数自然场景下的真实高光谱数据一般不会出现上述情况。
5 试验与分析 5.1 试验1试验1中的数据来自超光谱数字图像收集实验仪器(hyperspectral digital imagery collection experiment, HYDICE)在美国华盛顿特区采集的高光谱数据集,如图 1所示,大小为400×400像元。该数据原始波段数量210,波段范围400~2400 nm,波段宽度为10 nm,涵盖了可见光和近红外谱段范围;在去除900~1400 nm的大气吸收波段后,该数据剩余191波段。该数据可在美国地质调查局(United States Geological Survey)网站下载(https://speclab.cr.usgs.gov/spectral.lib04/lib04-HYDICE.html),同时可下载的还有该地区的实地调查报告及配套实测数据,据此可知该地区图像中主要含有水体、裸土和树木3种地物。

|
| 图 1 美国华盛顿特区HYDICE数据 Fig. 1 HYDICE data of Washington D.C., USA |
邻接规则选择queen(具有公共边界或公共顶点的像元为相邻像元),距离计算方法选择欧氏距离,邻接距离d设置为3(空间距离不大于3的像元互为相邻像元),根据式(20)计算整幅图像的全局Moran’I空间自相关指数,结果为0.502 6,说明各像元间的空间相关特征显著,这也是大部分真实高光谱遥感图像的共同特点
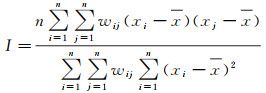 (20)
(20)
式中,n为样本量,即空间位置的个数;xi、xj是空间位置i和j的观察值;wij表示空间位置i和j的邻近关系,当i和j为邻近的空间位置时,wij=1;反之,wij=0。全局Moran指数I的取值范围为[-1, 1]。
利用HySime估算端元数量P,结果为3,这也验证了从地面实测报告得出的主要含有水体、裸土和树木3种地物的结论。因此,将解混试验的端元数量设置为3。由于HYDICE为机载光谱成像仪,空间分辨率高,图像中每种端元都含有大量纯像元。因此,通过在原图像中人工选择参考点的方式收集每种端元(地物)的光谱作为参考值,利用全约束最小二乘法计算端元的丰度参考值。
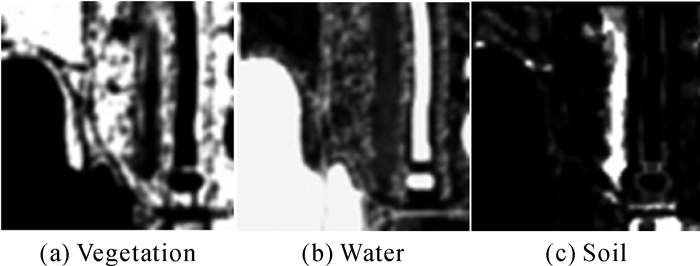
通过均值法重采样使图像的空间分辨率降低为原来的0.2倍。空间分辨率的大幅降低,形成了大量混合像元,便于验证S2CNMF算法。由于在地物范围确定的前提下,丰度分解结果的尺度是和空间分辨率大小严格对应的,同样利用均值法重采样技术把之前求出的端元丰度参考值进行聚合,得到行、列元素数量均为原始图像0.2倍的新图像丰度参考值,作为解混结果精度分析中的近似真值。降分辨率后的图像如图 2所示,降分辨率后图像的丰度参考值如图 3所示。图 3中纯白色代表端元在该像元内部面积比例为1(100%),纯黑色代表端元在该像元内部面积比例为0,其余各阶灰度分别对应0~1的不同比例。

|
| 图 2 降分辨率后的美国华盛顿特区HYDICE数据 Fig. 2 Resolution descended HYDICE data of Washington D.C., USA |

|
| 图 3 降分辨率后的美国华盛顿特区HYDICE数据丰度参考值 Fig. 3 Abundance reference of resolution descended HYDICE data of Washington D.C., USA |
试验选择如下比较方法:区域相关的NMF解混算法(ACBNMF)、最小化光谱相关度约束的NMF方法(MSCCNMF),这两种都是基于相关性分析的NMF解混算法。同时选择最小体积约束的非负矩阵分解(MVCNMF)作为比较方法,以评价提出的约束条件的有效性。MVCNMF目标函数包括两部分:①估计观测数据与端元和丰度重建数据之间的近似误差;②最小体积限制。
图 4—图 7分别列出了该数据的S2CNMF、ACBNMF、MSCCNMF和MVCNMF解混丰度估计结果。论文利用式(21)计算光谱角距离SAD,代表端元光谱分解精度
|
| 图 4 降分辨率后美国华盛顿特区HYDICE数据S2CNMF丰度估计 Fig. 4 S2CNMF's abundance estimation of resolution descended HYDICE data of Washington D.C., USA |

|
| 图 5 降分辨率后美国华盛顿特区HYDICE数据ACBNMF丰度估计 Fig. 5 ACBNMF's abundance estimation of resolution descended HYDICE data of Washington D.C., USA |

|
| 图 6 降分辨率后美国华盛顿特区HYDICE数据MSCCNMF丰度估计 Fig. 6 MSCCNMF's abundance estimation of resolution descended HYDICE data of Washington D.C., USA |

|
| 图 7 降分辨率后美国华盛顿特区HYDICE数据MVCNMF丰度估计 Fig. 7 MVCNMF's abundance estimation of resolution descended HYDICE data of Washington D.C., USA |
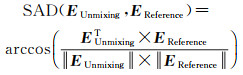 (21)
(21)
式中,EUnmixing表示某种端元在光谱解混结果中的端元光谱估计值;EReference表示某种端元的参考真值。
用εi, jk是第k个端元在图像位置(i, j)处像元的丰度余差,即丰度估计值与丰度真实值(参考值)的差,则第k个端元在整幅图像所有像元中均方根误差如式(22)所示,代表第k个端元的丰度分解精度
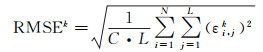 (22)
(22)
式中,L为高光谱图像波段数量;C为全部像元数量。
端元光谱和丰度解混的精度分析结果分别见表 1和表 2,其中粗体代表每一列的精度最高项。可以看出:4种解混算法均能以较为理想的精度有效分解出3种主要地物类型,其中本文提出的S2CNMF算法综合性能最好,以端元光谱分解结果为准,S2CNMF比其他3种算法的分解精度分别提高了12.8%、14.7%和15.0%;以丰度估计结果为准,S2CNMF比其他3种算法的分解精度分别提高了11.4%、13.7%和13.4%。上述结果表明,S2CNMF算法中空间和谱间相关性特征约束项的联合,对于克服NMF的局部极小问题,进一步提高解混精度具有积极意义和较理想能力。
| 解混方法 | 植被 | 水体 | 裸土 | 平均 |
| S2CNMF | 0.152 3 | 0.126 1 | 0.148 2 | 0.142 2 |
| ACBNMF | 0.176 8 | 0.146 7 | 0.165 5 | 0.163 0 |
| MSCCNMF | 0.172 9 | 0.156 4 | 0.170 6 | 0.166 6 |
| MVCNMF | 0.182 5 | 0.143 7 | 0.175 8 | 0.167 3 |
| 解混方法 | 植被 | 水体 | 裸土 | 平均 |
| S2CNMF | 0.125 8 | 0.121 5 | 0.140 1 | 0.129 1 |
| ACBNMF | 0.155 6 | 0.138 9 | 0.142 6 | 0.145 7 |
| MSCCNMF | 0.150 8 | 0.144 5 | 0.151 9 | 0.149 1 |
| MVCNMF | 0.155 3 | 0.143 4 | 0.153 7 | 0.150 8 |
此外,S2CNMF算法属于非监督算法,不需要像顶点成分分析(vertex component analysis, VCA)等基于纯像元的解混算法一样假设每种地物至少存在一个纯像元,不需要像文献[9—10]中提出的算法一样需要预知图像空间特征和地物分布规律,也不需要预知每种地物的具体种类和预先获取每种地物的光谱数据,只需要使用Hysime等方法预先估计出地物(端元)数量即可,因此对于解混先验知识的依赖程度较小,适用范围较广。
最后,在表 3给出了上述4种解混算法的运行时间。可以看出,4种算法的运算效率从高到低依次为:S2CNMF、ACBNMF、MSCCNMF和MVCNMF,其中S2CNMF和ACBNMF的运算效率比较接近,明显优于MSCCNMF和MVCNMF。究其原因,MSCCNMF为了度量多条光谱的相关程度,需要计算光谱相关度函数,而该函数是由每两条光谱协方差函数的平方和所组成的,由于每次迭代都需要计算光谱相关度函数,故算法整体计算时间较长;MVCNMF算法中的目标函数最小化是一个组合优化问题,MVCNMF采用交替非负最小二乘法(alternating nonnegative least squares)结合投影梯度学习法(projected gradient learning)求解该问题并实现非负约束,对应的迭代更新准则在求目标函数对丰度的偏导数过程中,涉及大量高阶矩阵的行列式计算,需要耗费大量时间,导致算法迭代速度较慢,运行时通常耗时较长。
| 解混方法 | S2CNMF | ACBNMF | MSCCNMF | MVCNMF |
| 运行时间/s | 85.67 | 99.72 | 186.64 | 232.73 |
5.2 试验2
试验1中,高光谱成像场景以成片分布的各类型农田为主,可以预见其空间相关性较高。为进一步验证算法对空间相关特征不显著场景的解混效果,试验2中的数据选择获取于1995年7月美国Nevada州Cuprite采矿区的AVIRIS高光谱数据,如图 8所示。图 8中的A、B、C、K、M等字样分别代表该地区5种广泛分布的矿物Alunite、Buddingtointe、Calcite、Kaolinite和Muscovite的大致分布位置。该图像大小为400列,350行,空间分辨率为20 m,波长范围为0.4~2.5 μm,光谱分辨率为10 nm,共224个波段,试验中剔除了存在水汽吸收和信噪比较低的波段,使用剩余的188个波段。该地区位于美国Nevada州南部,地表多为裸露矿物,基本无植被覆盖。相对于试验1中的数据,该数据的空间相关特征不明显,几种主要矿物空间分布的随机性较大。

|
| 图 8 Cuprite采矿区AVIRIS高光谱数据 Fig. 8 AVIRIS hyperspectral data of Cuprite mining field |
由于AVIRIS为机载光谱成像仪,空间分辨率(20 m)相对较高,可合理假设:对于每一种端元(地物),都能找到它具有较高丰度值的混合像元,这些混合像元的光谱数据可作为其中居主导地位的端元的光谱参考值。因此,通过在原图像中人工选择参考点的方式,收集每种端元(地物)的光谱作为参考值,利用全约束最小二乘法计算端元的丰度参考值。
重复试验1中的试验环节,对比和验证算法针对不同场景时的性能表现。需要说明的是,试验2只针对上述5种主要矿物类型进行解混试验,对于其余小目标代表的地物类型的假设和处理与数据1完全相同,具体情况不再赘述。
图 9为本文算法S2CNMF对应的Cuprite采矿区AVIRIS数据丰度估计结果。由于篇幅限制,MVCNMF等其他3种算法的结果图不再一一列出。

|
| 图 9 Cuprite采矿区AVIRIS数据S2CNMF丰度估计 Fig. 9 S2CNMF's abundance results of AVIRIS hyperspectral data of Cuprite mining field |
表 4和表 5分别给出了4种解混算法的端元光谱和丰度解混的精度分析结果。其中粗体代表每一列的精度最高项。可以看出:4种解混算法均能有效分解出5种主要矿物类型,其中本文提出的S2CNMF算法性能仍然最好,但与其余3种算法均比较接近。以端元光谱分解结果为准,S2CNMF比其他3种算法的分解精度分别提高了8.85%、10.8%和9.34%;以丰度估计结果为准,S2CNMF比其他3种算法的分解精度分别提高了6.27%、6.85%和8.03%。其余3种算法精度基本相当。
| 解混方法 | S2CNMF | ACBNMF | MSCCNMF | MVCNMF |
| Alunite | 0.212 2 | 0.225 7 | 0.237 5 | 0.240 1 |
| Buddingtointe | 0.198 7 | 0.213 8 | 0.220 8 | 0.226 7 |
| Calcite | 0.193 1 | 0.229 5 | 0.219 4 | 0.210 3 |
| Kaolinite | 0.198 5 | 0.205 6 | 0.223 6 | 0.223 8 |
| Muscovite | 0.212 4 | 0.237 9 | 0.235 5 | 0.217 5 |
| 平均 | 0.202 8 | 0.222 5 | 0.227 4 | 0.223 7 |
| 解混方法 | S2CNMF | ACBNMF | MSCCNMF | MVCNMF |
| Alunite | 0.212 2 | 0.219 3 | 0.223 6 | 0.241 2 |
| Buddingtointe | 0.199 8 | 0.222 5 | 0.219 4 | 0.217 9 |
| Calcite | 0.220 1 | 0.235 7 | 0.230 8 | 0.233 7 |
| Kaolinite | 0.215 2 | 0.231 9 | 0.227 7 | 0.235 8 |
| Muscovite | 0.206 7 | 0.215 3 | 0.230 1 | 0.217 5 |
| 平均 | 0.210 8 | 0.224 9 | 0.226 3 | 0.229 2 |
上述结果表明,本文算法在试验数据空间相关程度显著减小的情况下,相对于其他几种NMF代表性算法,解混精度的优势略有减小。分析其原因,试验数据空间相关程度的降低,会不可避免地导致算法基于空间相关特征的约束部分出现一定程度的性能下降;但由于算法还包括了谱段间的相关性约束,能够在较大程度上弥补空间相关约束部分解混性能降低带来的负面影响,在整体上仍保持较为理想的解混性能。
6 结论与展望论文结果表明,在NMF线性盲分解过程中分别利用MRF模型与复杂度映射,引入高光谱图像的空间与谱间相关特征约束,能够显著降低目标函数非凸问题带来的不利影响,相较于ACBNMF、MSCCNMF和MVCNMF等几种代表性NMF扩展算法,能够进一步改善解混精度。
相对于前人的研究成果,本文主要从3个方面进行了改进:①针对影响NMF线性盲分解性能的“局部极小”问题,在解混模型中同时构建空间与谱间相关性特征约束,增强了NMF解混模型对高光谱遥感数据特征的表述能力;②引入空间相关特征约束时,放弃了添加目标函数新约束项的传统做法,而是采用与NMF目标函数并行迭代的新形式,有助于简化算法模型,避免过多内部函数项之间的相互影响;③提出的属于非监督算法,能够降低对先验知识的依赖,相对于更为依赖先验知识的现有监督类算法,实用性进一步改善。
最后应当指出,尽管相关性特征在高光谱图像中普遍存在,但并非全部都同时具有显著的空间与谱间相关特征。如何进一步拓展适用范围,稳定算法性能,将是下一步研究工作的主要内容。
| [1] |
王毓乾.
基于空间-光谱分析的高光谱遥感影像稀疏解混研究[J]. 测绘学报, 2017, 46(8): 1072.
WANG Yuqian. Hyperspectral imagery sparse unmixing based on spatial and spectral analysis[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 1072. DOI:10.11947/j.AGCS.2017.20170167 |
| [2] |
张良培, 武辰.
多时相遥感影像变化检测的现状与展望[J]. 测绘学报, 2017, 46(10): 1447–1459.
ZHANG Liangpei, WU Chen. Advance and future development of change detection for multi-temporal remote sensing imagery[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1447–1459. DOI:10.11947/j.AGCS.2017.20170340 |
| [3] | LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788–791. DOI:10.1038/44565 |
| [4] | XU Yifei, DENG Shuiguang, LI Xiaoli, et al. A sparse unmixing model based on NMF and its application in Raman image[J]. Neurocomputing, 2016(207): 120–130. |
| [5] | KAROUI M S, DEVILLE Y, HOSSEINI S, et al. Blind spatial unmixing of multispectral images:new methods combining sparse component analysis, clustering and non-negativity constraints[J]. Pattern Recognition, 2012, 45(12): 4263–4278. DOI:10.1016/j.patcog.2012.05.008 |
| [6] | MUSHTAQ Q, HAQ I U, AHMAD M, et al. Hyperspectral blind unmixing and multiple target detection using linear mixture model[J]. Advanced Materials Research, 2012(488-489): 1224–1228. |
| [7] |
施蓓琦, 刘春, 孙伟伟, 等.
应用稀疏非负矩阵分解聚类实现高光谱影像波段的优化选择[J]. 测绘学报, 2013, 42(3): 351–358, 366.
SHI Beiqi, LIU Chun, SUN Weiwei, et al. Sparse nonnegative matrix factorization for hyperspectral optimal band selection[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 351–358, 366. |
| [8] |
张盈, 张景雄.
顾及空间相关性的遥感影像信息量的度量方法[J]. 测绘学报, 2015, 44(10): 1117–1124.
ZHANG Ying, ZHANG Jingxiong. Measure of information content of remotely sensed images accounting for spatial correlation[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1117–1124. DOI:10.11947/j.AGCS.2015.20140417 |
| [9] |
孔繁锵, 卞陈鼎, 李云松, 等.
非凸稀疏低秩约束的高光谱解混方法[J]. 西安电子科技大学学报(自然科学版), 2016, 43(6): 116–121.
KONG Fanqiang, BIAN Chending, LI Yunsong, et al. Hyperspectral unmixing method based on the non-convex sparse and low-rank constraints[J]. Journal of Xidian University, 2016, 43(6): 116–121. DOI:10.3969/j.issn.1001-2400.2016.06.020 |
| [10] | JIA Sen, QIAN Yuntao. Constrained nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(l): 161–173. |
| [11] | MIAO Lidan, QI Hairong. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 15(8): 765–777. |
| [12] |
詹锡兰, 吴波.
一种基于高斯马尔可夫随机场模型的混合像元分解方法[J]. 福州大学学报(自然科学版), 2011, 39(1): 60–66.
ZHAN Xilan, WU Bo. A method of spectral mixture analysis based on Gaussian Markov random field model[J]. Journal of Fuzhou University (Natural Science Edition), 2011, 39(1): 60–66. |
| [13] |
刘建军, 吴泽彬, 韦志辉, 等.
基于空间相关性约束稀疏表示的高光谱图像分类[J]. 电子与信息学报, 2012, 34(11): 2666–2671.
LIU Jianjun, WU Zebin, WEI Zhihui, et al. Spatial correlation constrained sparse representation for hyperspectral image classification[J]. Journal of Electronics & Information Technology, 2012, 34(11): 2666–2671. |
| [14] | CHEN Xiawei, YU Jing, SUN Weidong. Area-correlated spectral unmixing based on Bayesian nonnegative matrix factorization[J]. Open Journal of Applied Sciences, 2013, 3(1): 41–46. DOI:10.4236/ojapps.2013.31B009 |
| [15] |
王楠, 张良培, 杜博.
最小光谱相关约束NMF的高光谱遥感图像混合像元分解[J]. 武汉大学学报(信息科学版), 2014, 39(1): 22–26.
WANG Nan, ZHANG Liangpei, DU Bo. Minimum spectral correlation constraint algorithm based on non-negative matrix factorization for hyperspectral unmixing[J]. Geomatics and Information Science of Wuhan University, 2014, 39(1): 22–26. |
| [16] |
许宁, 尤红建, 耿修瑞, 等.
基于光谱相似度量的高光谱图像多任务联合稀疏光谱解混方法[J]. 电子与信息学报, 2016, 38(11): 2701–2708.
XU Ning, YOU Hongjian, GENG Xiurui, et al. Multi-task jointly sparse spectral unmixing method based on spectral similarity measure of hyperspectral imagery[J]. Journal of Electronics & Information Technology, 2016, 38(11): 2701–2708. |
| [17] | CHEN Bolin, LI Min, WANG Jianxin, et al. Disease gene identification by using graph kernels and Markov random fields[J]. Science China Life Sciences, 2014, 57(11): 1054–1063. DOI:10.1007/s11427-014-4745-8 |
| [18] |
尤传雨, 刘文波, 常军.
基于复杂追踪理论的结构模态参数识别[J]. 苏州科技学院学报(工程技术版), 2016, 29(2): 38–42, 50.
YOU Chuanyu, LIU Wenbo, CHANG Jun. Structural model parameter identification based on complexity pursuit[J]. Journal of Suzhou University of Science and Technology (Engineering and Technology), 2016, 29(2): 38–42, 50. |
| [19] | HOYER P O. Non-negative matrix factorization with sparseness constraints[J]. The Journal of Machine Learning Research, 2004(5): 1457–1469. |
| [20] | YIN Gang, BUI T. Stochastic systems arising from Markov modulated empirical measures[J]. Journal of Systems Science and Complexity, 2017, 30(5): 999–1011. DOI:10.1007/s11424-016-5248-4 |
| [21] | DENG Huawu, CLAUSI D A. Unsupervised image segmentation using a simple MRF model with a new implementation scheme[J]. Pattern Recognition, 2004, 37(12): 2323–2335. DOI:10.1016/S0031-3203(04)00195-5 |
| [22] |
亓琳, 史泽林.
一种基于DA-GMRF的无监督图像分割方法[J]. 光电工程, 2007, 34(10): 88–92.
QI Lin, SHI Zelin. Unsupervised image segmentation based on DA-GMRF[J]. Opto-Electronic Engineering, 2007, 34(10): 88–92. DOI:10.3969/j.issn.1003-501X.2007.10.018 |
| [23] | BIOUCAS-DIAS J M, NASCIMENTO J M P. Hyperspectral subspace identification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(8): 2435–2445. DOI:10.1109/TGRS.2008.918089 |
| [24] | GENG Xiurui, JI Luyan, SUN Kang. Non-negative matrix factorization based unmixing for principal component transformed hyperspectral data[J]. Frontiers of Information Technology & Electronic Engineering, 2016, 17(5): 403–412. |
| [25] |
吴金彪.
D-N交替迭代法及其收敛性分析[J]. 数值计算与计算机应用, 2002, 23(2): 121–130.
WU Jinbiao. D-N commutative method and its convergence[J]. Journal on Numerical Methods and Computer Applications, 2002, 23(2): 121–130. DOI:10.3969/j.issn.1000-3266.2002.02.006 |


